
👾, Хабр!
Вернёмся к классической модели. Две недели назад мы рассмотрели альтернативные окрестности для КА, из числа «признанных сообществом». Сегодня дополним эту тему интересными вариативными частностями, такими как «взвешенные окрестности» и «far corners»/«far edges».
Вариативными мы их называем потому, что за этими названиями скрываются не конкретные паттерны окрестностей, а целые группы, с дополнительными правилами построения.
:h Что здесь происходит (для новых читателей серии)
В этой серии мы разбираем клеточные автоматы – дискретную модель, основой которой является сетка из ячеек-клеток, которые изменяют (или не изменяют) своё состояние в зависимости от количества соседей.
Учёт соседей выполняется по указанным нами правилам. Вариаций правил существует бесчисленное множество, и они были систематизированы в определённые конфигурации.
Самая популярная конфигурация – «B/S», или «life-like», по названию крайне широко известного клеточного автомата «Game of Life», где B/S обозначает, что в нашем правиле мы описываем всего два параметра – количество соседей необходимых для рождения новой клетки в пустой ячейке, и количество соседей для выживания существующей клетки.
В каждой статье серии мы углубляемся в данную конфигурацию, добавляя новые параметры, либо дополняя существующие. Иногда заглядываем и в прочие конфигурации.
Для понимания сегодняшней статьи достаточно знать, что (продолжение под катом):
- поиск соседей изначально выполняется в радиусе 1 (=8 окружающих клеток), но мы можем установить и другой, добавив к правилу параметр Rx, где x – нужный нам радиус;
- мы можем изменять шаблон окрестности поиска соседей. Изначально подразумевается окрестность Мура – R в каждую сторону (и диагонали) от рассматриваемой клетки, – но указывая Nxx мы будем определять иной шаблон, что, конечно, изменит вид правила. Расширением этой части правила мы занимались две недели назад, и продолжаем сегодня;
- прочие расширения, рассмотренные на предыдущих неделях, не являются необходимыми для понимания сегодняшней статьи, но вы, конечно, можете предварительно ознакомиться с ними, для большей последовательности чтения. Ссылки в конце материала и в профиле.
❯ Far corners / Far edges
Начнём с «далёких углов/сторон».
Данный двойной шаблон, не встречается при стандартном перечислении окрестностей, хотя в этом списке ему самое место, да и в нотации обозначается там же. За основу берётся уже столь привычная нам окрестность Мура, и, в зависимости от дополнительных параметров окрестности, клетки соответствующие «сторонам» и «углам» выносятся на указанный радиус. Если никаких параметров не указано – выносятся на максимальный радиус R. Вот так это выглядит без дополнительных параметров:

Вид окрестности на радиусах 1-4
В нотации данная окрестность обозначается как NF, однако на этом не заканчивается. Дополнительно в данном шаблоне мы можем указывать отдаление, раздельно для «углов» и «сторон», добавляя в нотации соответствующие параметры, прямо в указании окрестности. Например, мы можем вынести углы, но оставить стороны на ближайшем радиусе – NFe1. Аналогично для «далёких сторон» – NFc1. Пропущенные параметры приравниваются к R, а потому указывать оба атрибута нам никогда не понадобится, если мы не укажем избыточный R, который, в этом случае, станет ложным параметром. Но, это всё ещё возможно: R3/B…/S…/NFe2c1 – так мы, например, получим контур окрестности фон Неймана для R2, при указанном (и неиспользуемом) R3 – ![]() . Значение 0 стандартом не предусмотрено (и, соответственно, в популярных симуляторах не реализовано), но было бы неплохим дополнением, чтобы обозначать использование только углов или только сторон. Мы взглянем и на это дополнение.
. Значение 0 стандартом не предусмотрено (и, соответственно, в популярных симуляторах не реализовано), но было бы неплохим дополнением, чтобы обозначать использование только углов или только сторон. Мы взглянем и на это дополнение.
Перейдём к примерам.
Какую бы конфигурацию и расширение клеточного автомата вы бы не открыли, вы в любом случае найдёте переложение правила классической «Жизни» на данную вариацию. В случае с NF, мы получаем до абсурда очевидное поведение – все фигуры становятся разреженными, со значением R:

52с., 224×224, 150×20% | R2/G2/S2-3/B3/NF
:h Нотация
R – радиус поиска соседей. Регулирует окрестность.
G – количество состояний клеток. Минимум – 2 (жива/мертва), бо́льшие значения отвечают за длительность «старения» клетки, когда она уже не считается живым соседом для прочих клеток, но ещё не освободила клетку для рождения новой. Если совсем правильно, в HROT и LtL принято использовать обозначение C (Count of states).
S – значения и/или диапазоны количества соседей, необходимых для выживания клетки. Диапазоны записываются через дефис (может быть использовано двое- и троеточие или t), значения и диапазоны отделяются друг от друга запятыми.
B – полностью аналогично S, но отвечает за количество соседей, необходимых для рождения новой клетки.
N – обозначение используемой окрестности.
/ – разделитель между параметрами правила. В правильной нотации используются «,» (да, и между параметрами, и между диапазонами/значениями), но также встречается и вариант вовсе без разделителей между параметрами.
Характеристики примера – длительность анимации; [ускорение анимации от 100мс. на фрейм, если есть]; размер поля; размер и процент центрального заполнения на старте.
Здесь все наши пекарни, баржи, ульи, караваи, и даже глайдеры. Хотя, конечно, это и не полный эквивалент «Жизни», но то же ружьё Госпера мы всё равно можем реализовать:

45с., 224×224 | R2/G2/S2-3/B3/NF
.rle
Примеры с конкретным стартовым расположением будем сопровождать правилами, которые могут быть обработаны популярными симуляторами КА, такими как LifeViewer и Golly.
Не обращайте внимания на то, что нотация в нашей серии несколько отличается. Это сделано для большей последовательности изложения и читаемости.
Так как Golly не принимает NF, окрестность приходится указывать в ручном формате. Но об этом мы поговорим в другой раз.
x = 0, y = 0, rule = R2,C2,S2-3,B3,N@A82415
48bo2$44bo3bo2$24bobo13bobo25bobo2$22bo7bo9bobo25bobo2$obo17bo11bo7bobo2$obo17bo7bo3bobo9bo3bo2$20bo11bo15bo2$22bo7bo2$24bobo!
Нагляднее всего вариации NF окрестностей представляются на орнаментных видах.

9с., 224×224, 1×100% | R3/G2/S1-5/B1,3/NFe2c3

17с., 224×224, 1×100% | R5/G5/S1-6/B1,3,5/NFe5c1

14с., 224×224, 1×100% | R3/G3/S0-4/B1,4/NFe3c0

17с., 224×224, 1×100% | R9/G3/S0-2,4/B1,4/NFe0c9
Сам по себе, шаблон ещё менее популярен, чем рассмотренные нами ранее окрестности, однако является интересный расширением и часто встречается как часть нашей следующей, на сегодня, темы.
❯ Взвешенные окрестности
До сего момента, вне зависимости от конфигурации, окрестности и любых других параметров, при рассмотрении соседей мы всегда принимали одну живую соседнюю клетку за единицу в счётчике соседей (в случае нотации Хенселя – в шаблоне расположения). Коррективу в этот подход вносят взвешенные окрестности, где мы задаём каждому потенциальному соседу свой вес, а правила рождения/выживания описываем от суммы весов живых соседей.
Во взвешенных окрестностях стоит выделить два момента:
- за основу опять берётся окрестность Мура, как самая полная, так как на её основе можно описать любую взвешенную окрестность. И даже альтернативные окрестности позапрошлой недели можно описать просто весами, задав необходимые нули на поле единичных весов;
- центральная клетка включается в общее перечисление, и для её пропуска необходимо явно указывать 0 в центральной позиции.
Окрестность Гаусса
Самой популярной и интуитивной является окрестность с весами по распределению Гаусса:

Веса окрестности на радиусах 1-4
Центральная клетка включена в счётчик, и в классическом виде не переопределяется.
Окрестность Гаусса – единственный паттерн взвешенной окрестности, который имеет собственное устоявшееся обозначение в нотации – NG. Это, конечно, связано и с тем, что паттерн включает в себя множество разных частных окрестностей, так как веса зависят от радиуса.
Данная окрестность строится по правилу (R + 1 - abs(y)) * (R + 1 - abs(x)), где R – радиус окрестности, а x и y – координаты отдельной клетки, от центральной (0, 0).
Несколько примеров:

47с., 224×224, 150×30% | R2/G3/S30-48/B24-36/NG
Переложение правил «Жизни» здесь выглядит необычно, и, если не знать, то сложно представить, что этот вид – B3/S23.

51с., 224×224, 20×20% | R1/G2/S2-3/B3/NG
Ещё одним очень популярным шаблоном для построения правил, который также часто можно встретить на различных конфигурациях, являются правила «все [не]чётные S и все [не]чётные B», в четырёх вариациях. Этот шаблон настолько популярен, что для него стоило бы выделить отдельное обозначение в нотации, но пока это нигде не реализовано.

22с., 224×224, 1×100% | R1/G3/S1,3,5,7,9,11,13,15/B1,3,5,7,9,11,13,15/NG
Больше примеров
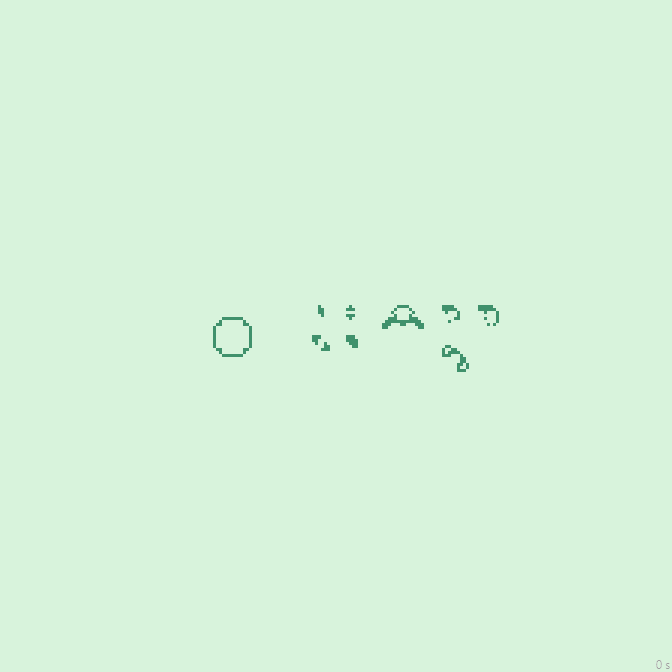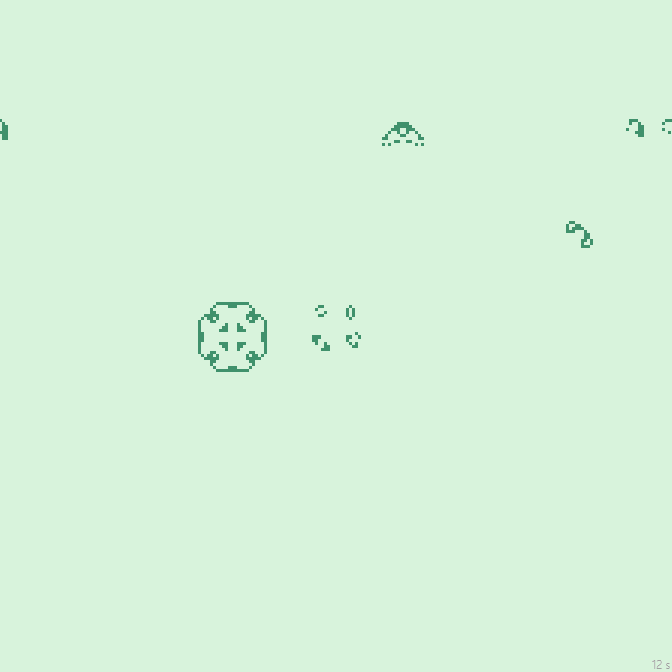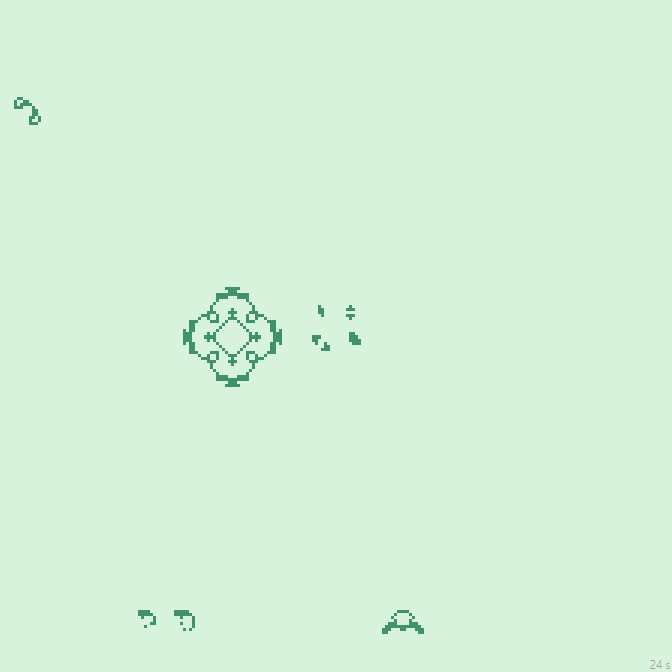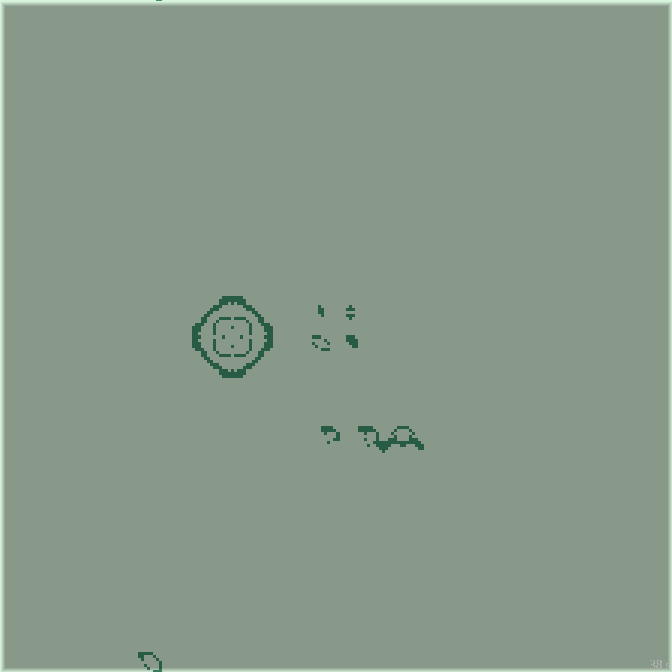
38с., 224×224 | R2/G2/S20-31,43/B20-31/NG
.rle
x = 0, y = 0, rule = R2,C2,S20-31,43,B20-31,NG
35bo9bo15b4o11b4o8b5o$35b2o7b3o13bo4bo10b5o7b6o$35b2o22bo6bo10bo3bo8bo3bo$36bo7b3o13bo4bo15bo12bo$3b7o35bo12b3o4b3o12b2o8bo3bo$2bo7bo46b12o9bo15bo$b2o7b2o44b3o3b2o3b3o21bobo$o11bo43b2o10b2o$o11bo$o11bo$o11bo20b3o8b3o$o11bo20b2o9b4o$o11bo21bo2bo7b3o$o11bo24b2o7b2o29b2o$b2o7b2o24b3o37bo2b2o$2bo7bo65bob4o$3b7o66b3o3bo$82b2o$82b2o$81b2obo$81bo2bo$81b3o!
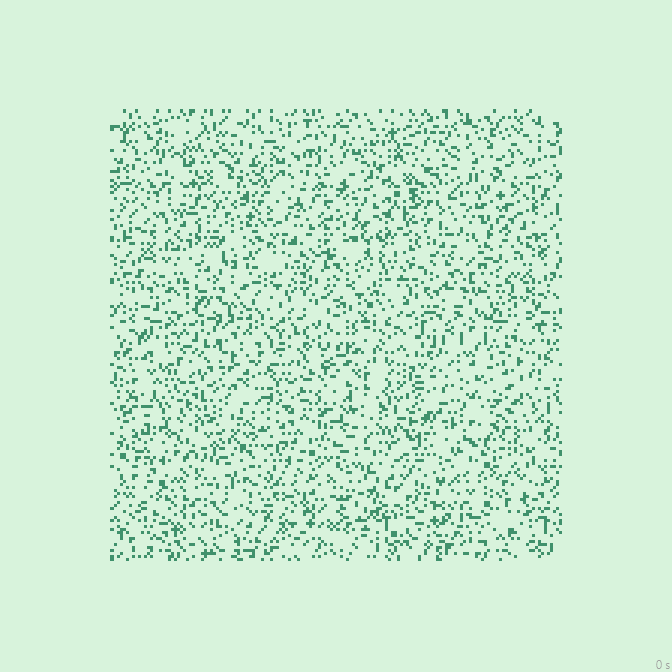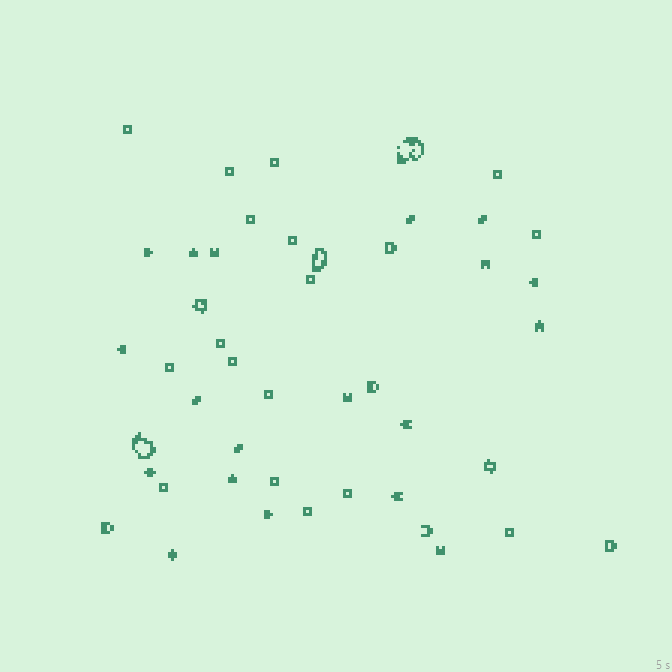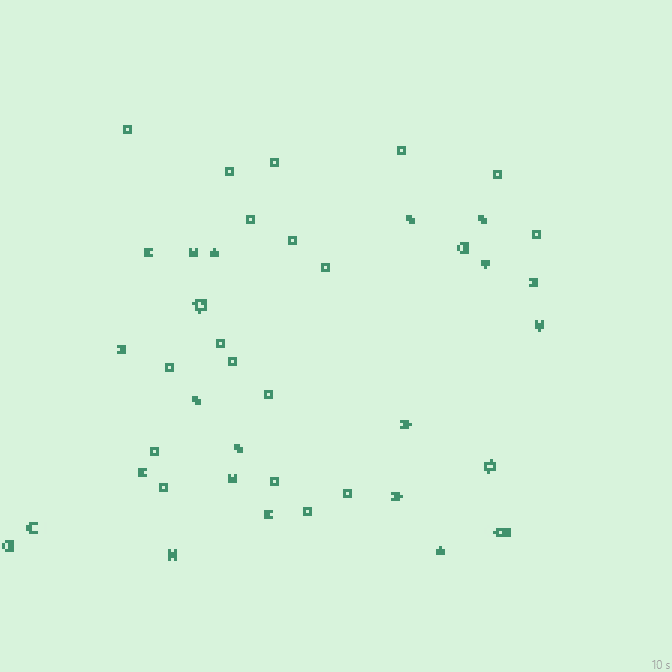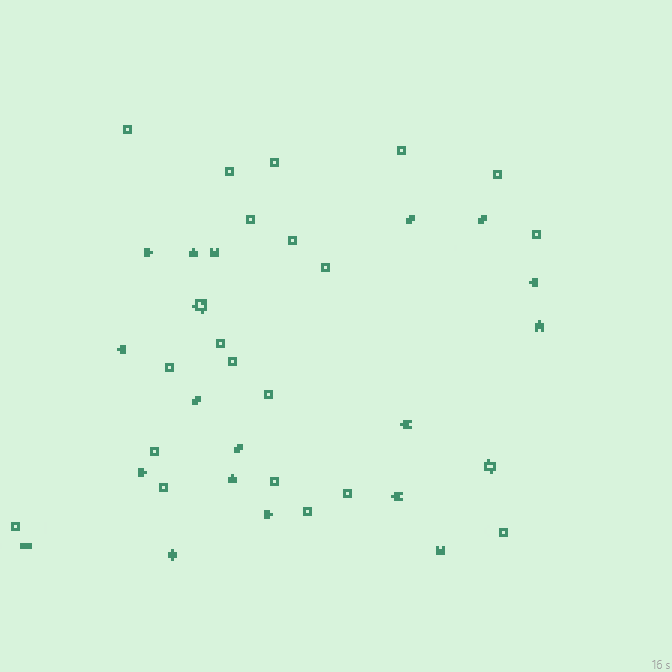
16с., 224×224, 150×20% | R2/G2/S31-48/B24-38/NG

32с., 224×224, 150×20% | R2/G2/S24-36/B20-31/NG
И напоследок взглянем на странное, во всех отношениях, правило, с очень необычным финальным состоянием.
Правило: чётные S, нечётные B, R=4
R4/G2/S0,2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50,52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,98,100,102,104,106,108,110,112,114,116,118,120,122,124,126,128,130,132,134,136,138,140,142,144,146,148,150,152,154,156,158,160,162,164,166,168,170,172,174,176,178,180,182,184,186,188,190,192,194,196,198,200,202,204,206,208,210,212,214,216,218,220,222,224,226,228,230,232,234,236,238,240,242,244,246,248,250,252,254,256,258,260,262,264,266,268,270,272,274,276,278,280,282,284,286,288,290,292,294,296,298,300,302,304,306,308,310,312,314,316,318,320,322,324,326,328,330,332,334,336,338,340,342,344,346,348,350,352,354,356,358,360,362,364,366,368,370,372,374,376,378,380,382,384,386,388,390,392,394,396,398,400,402,404,406,408,410,412,414,416,418,420,422,424,426,428,430,432,434,436,438,440,442,444,446,448,450,452,454,456,458,460,462,464,466,468,470,472,474,476,478,480,482,484,486,488,490,492,494,496,498,500,502,504,506,508,510,512,514,516,518,520,522,524,526,528,530,532,534,536,538,540,542,544,546,548,550,552,554,556,558,560,562,564,566,568,570,572,574,576,578,580,582,584,586,588,590,592,594,596,598,600,602,604,606,608,610,612,614,616,618,620,622,624/B1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,71,73,75,77,79,81,83,85,87,89,91,93,95,97,99,101,103,105,107,109,111,113,115,117,119,121,123,125,127,129,131,133,135,137,139,141,143,145,147,149,151,153,155,157,159,161,163,165,167,169,171,173,175,177,179,181,183,185,187,189,191,193,195,197,199,201,203,205,207,209,211,213,215,217,219,221,223,225,227,229,231,233,235,237,239,241,243,245,247,249,251,253,255,257,259,261,263,265,267,269,271,273,275,277,279,281,283,285,287,289,291,293,295,297,299,301,303,305,307,309,311,313,315,317,319,321,323,325,327,329,331,333,335,337,339,341,343,345,347,349,351,353,355,357,359,361,363,365,367,369,371,373,375,377,379,381,383,385,387,389,391,393,395,397,399,401,403,405,407,409,411,413,415,417,419,421,423,425,427,429,431,433,435,437,439,441,443,445,447,449,451,453,455,457,459,461,463,465,467,469,471,473,475,477,479,481,483,485,487,489,491,493,495,497,499,501,503,505,507,509,511,513,515,517,519,521,523,525,527,529,531,533,535,537,539,541,543,545,547,549,551,553,555,557,559,561,563,565,567,569,571,573,575,577,579,581,583,585,587,589,591,593,595,597,599,601,603,605,607,609,611,613,615,617,619,621,623,625/NG
Вид немного мерцает, потому каждый второй фрейм обрезан.
![R4/G2/S[чёт]/B[нечёт]/NG | 16с., 672×672, 1×100%](https://habrastorage.org/webt/wu/o0/sw/wuo0swuxglvowudod3u8-v9cjzq.gif)
16с., 672×672, 1×100% | R4/G2/S[чёт]/B[нечёт]/NG
У меня нет никакого объяснения финального состояния. ¯\_(ツ)_/¯
Пользовательские взвешенные окрестности
В пользовательских взвешенных окрестностях задаётся конкретное значение веса для каждой клетки, по всей окрестности Мура с радиусом R. Здесь уже нет вариативности – одно правило задаёт ровно один вид для одного радиуса. Если вы хотите изменить радиус, вместе с ним придётся изменить и веса.
Согласно общепринятой нотации, веса указываются прямо в обозначении окрестности, без разделителей – NWxx...x, где x – вес, в порядке одномерного представления окрестности, в шестнадцатеричном виде. Значениями [0, 7](16) обозначаются соответствующие положительные веса, а значениями [8, f](16) – отрицательные [0, -7](10). Если требуются значения больше, все шестнадцатеричные представления становятся двухразрядными – [00, ff], с тем же распределением положительных и отрицательных – [00, 7f], [80, ff]. Трёхразрядная и более запись теоретически может быть использована, но не поддерживается известными симуляторами КА, и соответствующие правила в интернете вряд ли существуют.
Что же, перейдём к примерам.
Мы уже упоминали любовь пользователей смотреть на поведение B3/S23 на каждой новой конфигурации, но есть и обратный – добиваться на новых конфигурациях поведения GoL, по их правилам. Зачастую, с некоторыми особенностями. Один из таких примеров, который можно назвать Chaos Life, устанавливает в окрестности Мура с R1 вес 7, а на наиболее удалённых клетках с R10 по осям и диагоналям от центральной клетки – вес 1. Вот мы и встретились с NF, узнали?
Веса описываются в 441 символ, потому скроем их спойлером.
R10/G2/S3,13-22/B3,20-22/NW100000000010000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000777000000000100000000707000000001000000000777000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000010000000001

60с., 224×224, 20×150% | R10/G2/S3,13-22/B3,20-22/NW…
У данного правила есть интересные стартовые состояния:

27с., 224×224 | R10/G2/S3,13-22/B3,20-22/NW…
.rle
x = 0, y = 0, rule = R10,C2,S3,13-22,B3,20-22,NW100000000010000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000777000000000100000000707000000001000000000777000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000010000000001
2o8b2o8b2o$bo9bo9bo!

36с., 224×224 | R10/G2/S3,13-22/B3,20-22/NW…
.rle
x = 0, y = 0, rule = R10,C2,S3,13-22,B3,20-22,NW100000000010000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000777000000000100000000707000000001000000000777000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000010000000001
17b2o$17b2o$15b2o$15b2o7$8bo8b2o8b2o$8bo8b2o9bo$15b2o8bo$5b2o8b2o8b2o7$7bo9b2o$17b2o$5bo9b2o$15b2o25$60b2o$60b2o9$70b2o$70b2o9$40b2o$40b2o9$50b2o$50b2o9$20b2o$20b2o9$30b2o$30b2o9$2o$2o9$10b2o$o9b2o25$17b2o$17b2o$15b2o$15b2o7$8bo8b2o8b2o$8bo8b2o9bo$15b2o8bo$5b2o8b2o8b2o7$7bo9b2o$17b2o$5bo9b2o$15b2o!
Схожая идея, на меньшем радиусе и у правила R4/G2/S2-3,10,14-16/B3,14-16/NW[вес для R1 – 5, вес для FE и FC – 1]. Данное правило допускает одновременно и фигуры стандартного GoL, и их разреженные варианты, за счёт NF, как в начале этой статьи. Глайдеры на R4 смотрятся особенно забавно.

38с., 224×224 | R4/G2/S2-3,10,14-16/B3,14-16/NW…
.rle
x = 0, y = 0, rule = R4,C2,S2-3,10,14-16,B3,14-16,NW100010001000000000000000000000555000100505001000555000000000000000000000100010001
99bob4o4bob4ob3obobobo3b2o4bob3o$97b2o2b2obobo2bo2b2obobobo3b2ob4obo4bo2b2o$100bo2bo2b2o2bobobobo3b2o4b6o4b2obo$100bo2b3o6bobob6o2bo2bo2bob2ob2obobo$98b3o3b3o2bob5o4b4obo3b3o4bo$97bob4o3b2o3bob6o2b2o2bobobo2bobob2ob2o$99b2ob3o2bo3bobo2b3obob5obobo4bob2o$97b2obob2o5b3obo2bo3b3ob2o2bo2bo3bo3bo$97b3obo2bo2b4o2b3obob3o2b3o2bobo2bobo$97bobobobo4bo11b3o2bobobobo2b3ob3o$99b3o3bo3bo2b2o3bo2bob9o4bob2o$100bobobob2ob3obo2bo2b2obobo3bob2obo2bobobo$97bo3bob3obob2o2bo4bob3ob2obo2bo3b2o2bobo$97bob2o2b3obob2ob2o5b4o2bo7b2o2b3o$98b2obo8bo2b5obo5bobob3obo2b2ob2o$63b4o30b2obo2b2o4b2ob2o2bo2b2obobo4b2o2b2o2b3o$63bo3bo31b3o4b2ob2o2bob2ob2o3bobobo2bobobo4bo$63bo33b3obobob2obo2b6obobob3o3bo3b2ob4o$64bo32b4o2bo3bob5o2b2o2bob4o5b2ob2obob2o$98b2ob2o2bo2b2obo3b3ob2ob4o2bobobo2bo2b2o$97b2ob2ob3o3b3obob3o2b3obobo2b3o3b2o2b2o$99bobobob4o2b2o3bob2o2b6ob2o2b7o$98b4obo3bob2obobob3obo3b4obobobo5bo$97b2obo3b3obo4bo3b2obob3o2b3o2bo2bo2b2o$97bo4b3o3bo2bobob3o2bo7bo2bo2bo3bobo$99b2o6b2o2b5o4b2o3b2o2bobob2o4b2o$99b2o2b2ob2obobob2obobobo3bo6bob3obobo$98b2o2bob3o4b5obo4b3o4b2o4bob3o$98bo2bob5ob3ob2o5b2o2b2o3b3o4bob2o$99bo2bobobo6b2obobobo5b3ob4o2b2obo$99bobo2bobo2bo3bo4b3o5b8ob2obo$98bob2obo2b3o4b7ob3o3b2o2b2ob4o2bo$97b2ob3o2bob2o2bob2obo2bo2b2obo2b2ob2o2bobo$100bob7o3b4o3b2o2bo4bo3bobobo3bo$97bo5b2o2bo3b3obobo2bo3bob2o2bo4b5o$97bob2obobo4b2o2bo2b3ob3ob2o3b2o2bo2bob2o$97bo4bob3obo3bo2bo2b3o2b3o3bobobo2b3obo$97b2ob2o2b2ob5ob4ob2ob2obob2o2bob2obo$97bobob4obo4bo2b2ob2o4bobobobo2b3obo3bo$98b3o2b2o3bob3o2b4ob2o2bo2bo3b2ob2obobo$103bo4bobo2bo3bo3bo2b2ob2o2b2obo2b2o$o3bo3bo3bo3bo3bo3bo3bo3bo3bo60bo4b4o2b3o3bo2bo2b4o2bobob3obo3b2o$97bobo4b2o4b3ob3obo2bo2b3obo2b2o2bobobo$98b3o3b2obo2b2o3b3o3bobob2ob6ob2o2bo$97b2o3bo5bobob2ob2obo4b7o2b4obo2bo$97b5obobob2o4bobob5o3b3ob3o2bob2o2bo$97b5ob2o3b2obob4obo5b4o3bob3obo2bo$99b2o2bob2obob2obo2bobob2o3bo2b2o2bo2b3ob2o$100b4o4b2obo3bobo3b6o3b5o2bo2bo$98bobo3bo2bob2o2b6ob2o2b3o3b5o3b2o$100bo2b3obo2bo3bo3b2o2bobob2ob3obob2obo$99b4obob3obobobo2bob2ob2o4b2obo2bo2bobo$99bob3ob2o2bo2b4ob4o3bo7b3ob2obo$98b2ob2ob5o5bobob4obo2bo3bob2o3bo2bo$98bob2o5bo4b5o2bo2b3o4bobob3o4bo$97b3obo2bobob2obo2bo5bobo2b6o3bo$97b2o2bobo3b2obo2b4o4b6o3b2o2bob2o$97b5ob4ob2o4b5o2bo6b2obo3b2obo$97b3o2b3ob2o2bob3o2b3ob2ob2o2b4o4b5o$100bob2o3b2obo4b2o2bo4b4obobo4b2obo$97bo4b6o2b2ob3o3b2o5b2o2b2o2b2o2bo!
Один из пользователей также применил взвешенное правило с дополнительными Far Corners для «сдерживания» кораблей на правиле R6/G2/S4-6/B6/NW[R1 – 2; FC – 1]:

31с., 224×224 | R6/G2/S4-6/B6/NW…
.rle
x = 0, y = 0, rule = R6,C0,S4-6,B6,NW1000000000001000000000000000000000000000000000000000000000000000000000222000000000020200000000002220000000000000000000000000000000000000000000000000000000001000000000001
2o17b2o$2o17b2o$70b2o17b2o$70b2o17b2o$79b3o$79bobo$79bobo15$9b3o$9bobo$9bobo30$2o17b2o$2o17b2o$72b3o11b3o$72bobo11bobo$72bobo11bobo6$9b3o$9bobo$9bobo!
Больше всего сообществу нравится находить на взвешенных правилах различные конфигурации необычных кораблей. Ими и закончим сегодняшний материал.
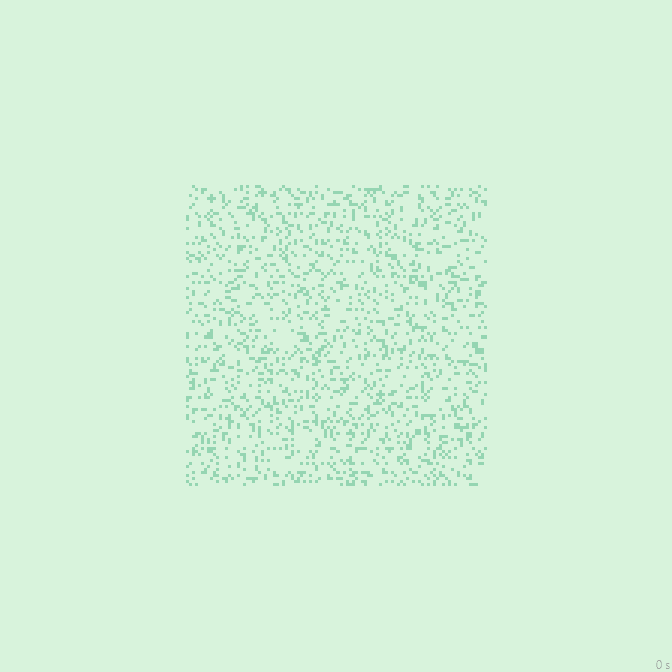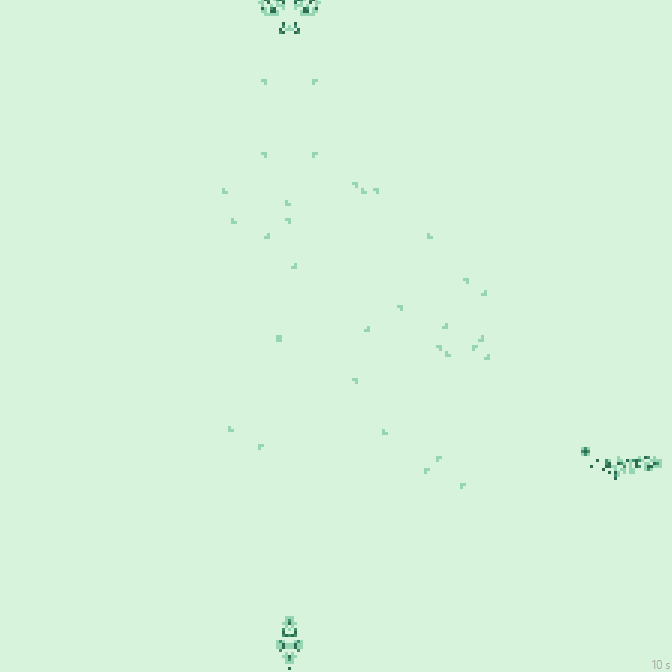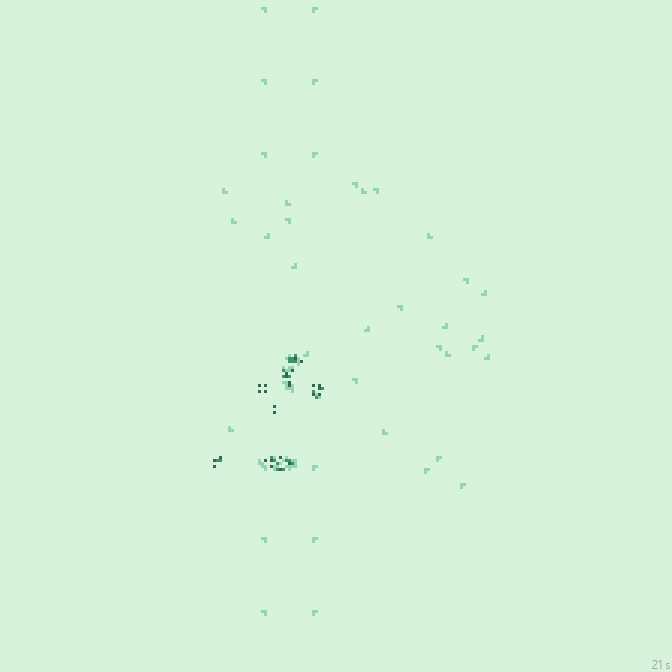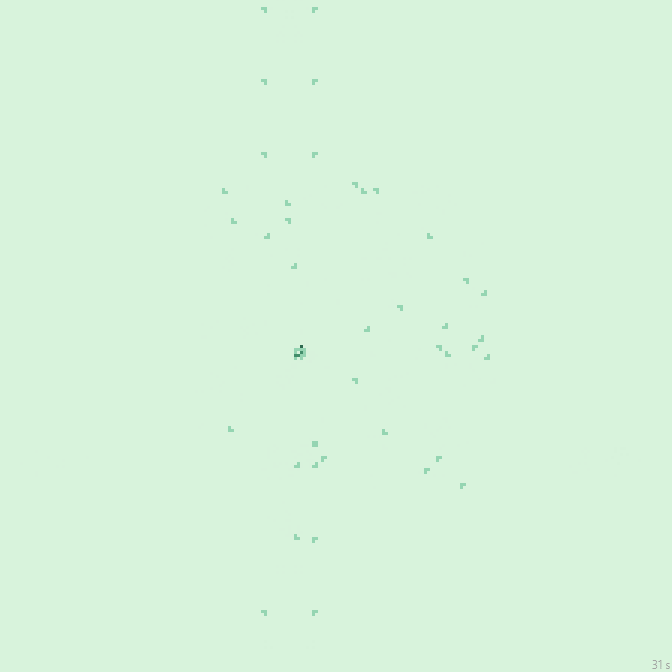
32с., 224×224, 100×20% | R2/G4/S5-9/B6-7/NW
10001
02320
03030
02320
10001

35с., 224×224, 100×20% | R2/G2/S0,5/B3/NW
00100
00200
12021
00200
00100

28с., 224×224, 100×20% | R2/G2/S2,4/B3/NW
00100
00200
12021
00200
00100
NW0100010100000100444000040400004440010000010100010:

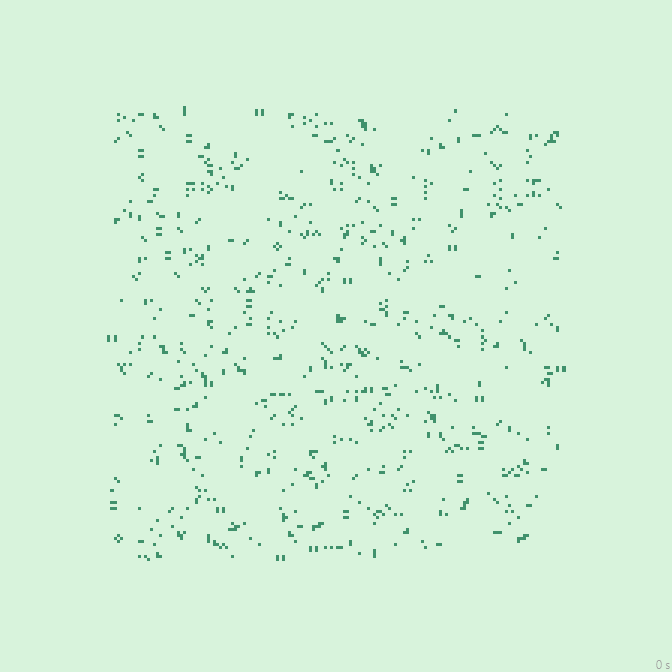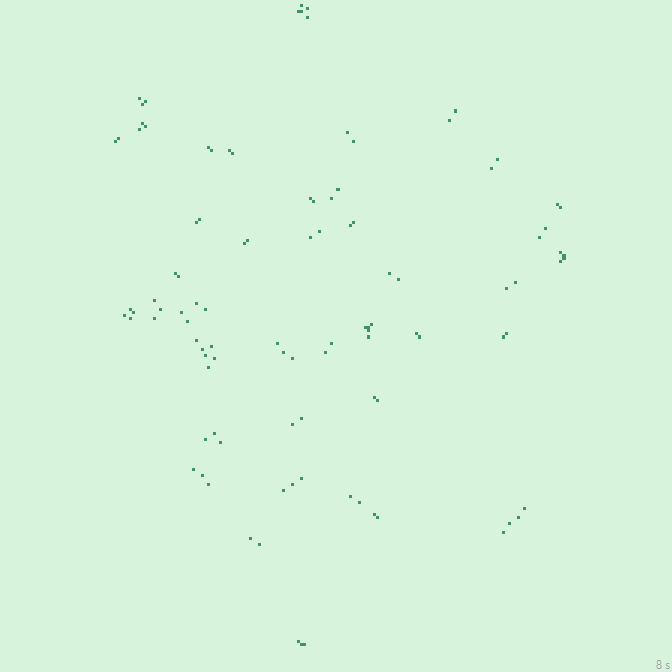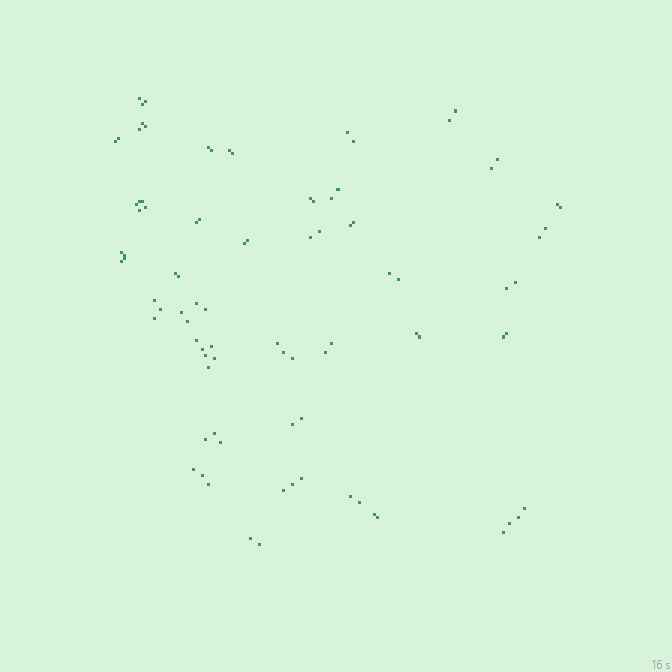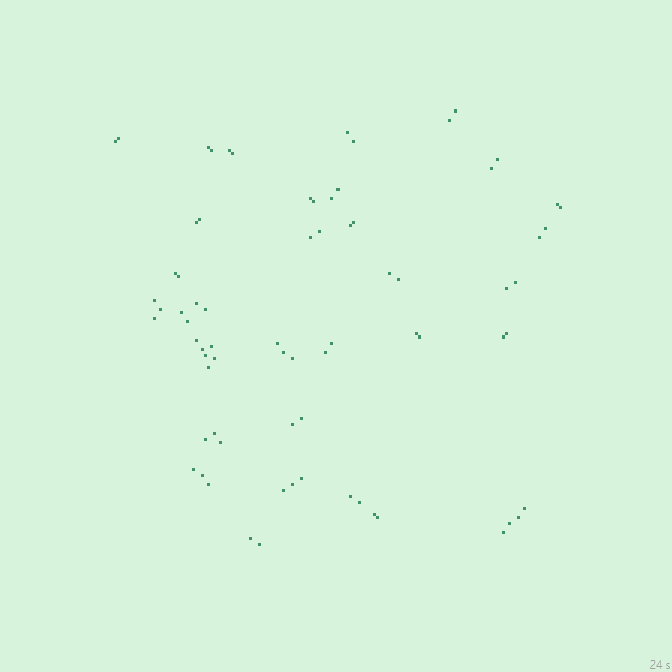
24с., 224×224, 150×5% | R3/G2/S1-3/B7-8,14-15/NW…
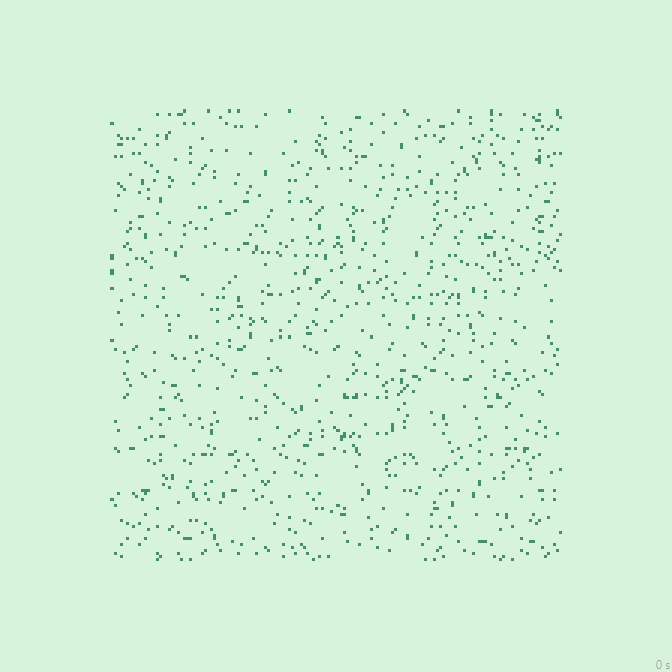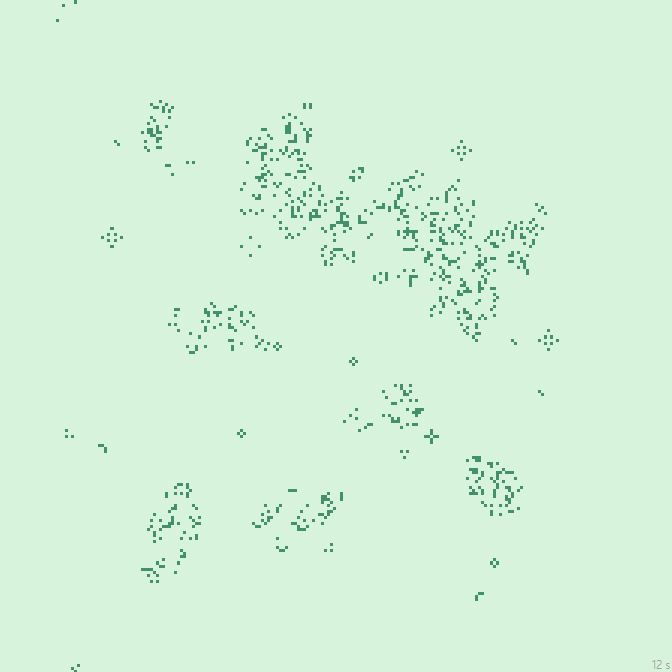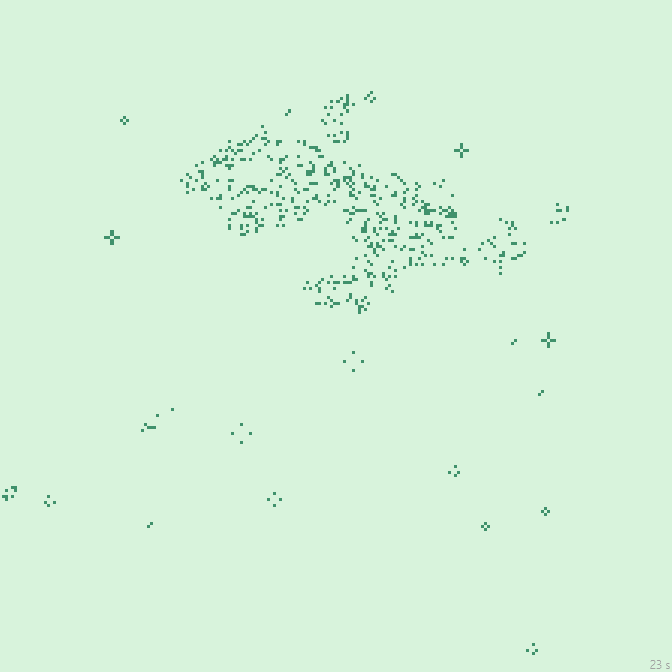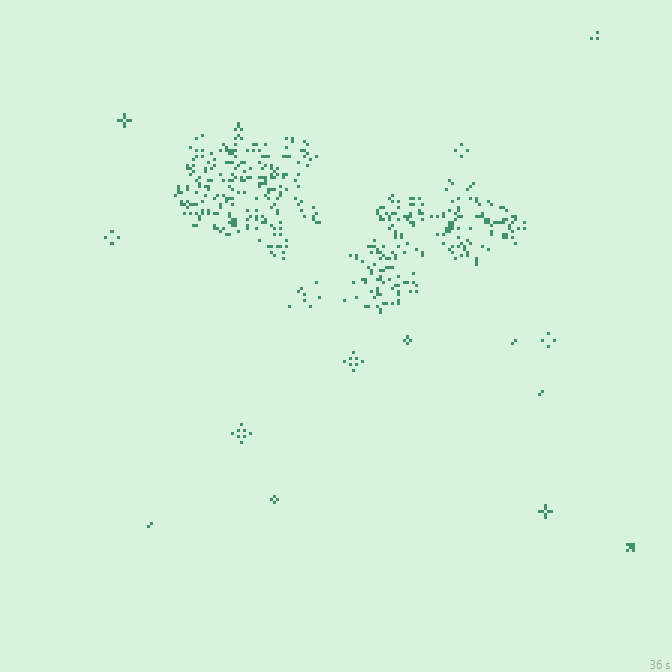
36с., 224×224, 150×5% | R3/G2/S2/B6-8/NW…
Мерцание

25с., 224×224, 150×5% | R3/G2/S/B4/NW…
Сегодня мы познакомились с несколькими новыми расширениями стандартной модели и новым подходом к оным.
На следующей неделе закроем тему окрестностей для данного поля, насколько это вообще возможно.
Не переключайтесь.
Читайте также
О клеточных автоматах:
- Базовая «life-like» конфигурация
- Старение клеток: параметр поколений
- Нотация Хенселя: учёт расположения соседей
- LtL: расширенный радиус поиска соседей
- Циклические клеточные автоматы
- Альтернативные окрестности и HROT
- Блочные КА, окрестность Марголуса
- Взвешенные окрестности, окрестность Гаусса, Far Corners/Edges (вы здесь)
- Моделирование лесных пожаров: теория, клеточный автомат на Python
- Сегрегация общества: модель Шеллинга и распределение этнических групп в городах Израиля
Прочее:
- 🟢 История моделирования лесных пожаров
- 🟠 REcollapse: фаззинг с использованием unicode-нормализации
- 🔵 Хватит использовать [a-zа-яё]: правильная работа с символами и категориями Unicode в регулярных выражениях
- 🟢 Краткая история календаря и фантазии о шестидневной неделе
- 🟢 Пройти LeetCode за год: экскурсия по сайту и roadmap
← Предыдущая часть | Следующая часть (TBA) →



