 Пауль де Вос. Бык, поверженный собаками. 1638–1640 гг. Музей Прадо, Мадрид.
Пауль де Вос. Бык, поверженный собаками. 1638–1640 гг. Музей Прадо, Мадрид.
В предыдущей части мы выяснили, как сформулировать на языке математики задачу поиска оптимального портфеля. В этой части вы узнаете:
— как составить оптимальный с точки зрения риска и доходности портфель, не углубляясь в суровую математику (посмотреть на рыночную капитализацию активов);
— как заработать что-то сверх безрисковой процентной ставки (взять на себя риск и на дистанции заработать премию за этот риск);
— любой ли риск вознаграждается премией (нет, только систематический);
— от чего зависит ожидаемая будущая доходность отдельной акции (главным образом, от ковариации со всем рынком);
— сколько зарабатывали инвесторы в рынок акций США (порядка 7–9% в год сверх безрисковой ставки);
— почему так много (возможно, люди не полностью рациональны и преувеличивают рискованность акций);
— можно ли предсказать будущую доходность рынка акций (скорее всего, нет);
— как осадить трейдера на коктейльной вечеринке (спросить, какой у него Шарп).
Оптимизация с безрисковым активом
Продолжим изучать задачу оптимизации портфеля. Неужели теперь каждый инвестор должен учить эту теорию и умножать в уме матрицы на 500 строк, чтобы собрать оптимальный портфель? К счастью, если добавить в задачу ещё кое-что, то математика резко упрощается.
Предположим, что на рынке есть не только четыре актива из таблицы 1.4, но и особый безрисковый (risk free) актив, который имеет нулевое стандартное отклонение. Проще говоря, будущая доходность безрискового актива — это не случайная величина, а константа.
Примером такого актива могут быть краткосрочные облигации Казначейства США (Treasury bills). Если вы сейчас покупаете за $999 облигацию, по которой через месяц правительство США обязуется выплатить $1 000, то вы точно знаете свою будущую доходность. По формуле (1.1) получается $1 000 ∕ $999 − 1 ≈ 0.1%. Не так много, зато наверняка. За последние 230 лет был всего один случай, когда из-за нерасторопности бухгалтерии выплаты задержались на несколько дней [Mar11], но ничего серьёзнее пока не случалось.
Итак, добавим к нашим четырём активам пятый — безрисковые облигации с ожидаемой доходностью 4% (чтобы график выглядел симпатично) и стандартным отклонением 0%, как в таблице 2.1. Кроме того, сделаем ещё одно допущение. Предположим, что инвесторы в нашей модели могут занимать деньги под безрисковую процентную ставку (то есть под 4%). Тогда новая граница эффективности будет выглядеть как на рисунке 2.1.
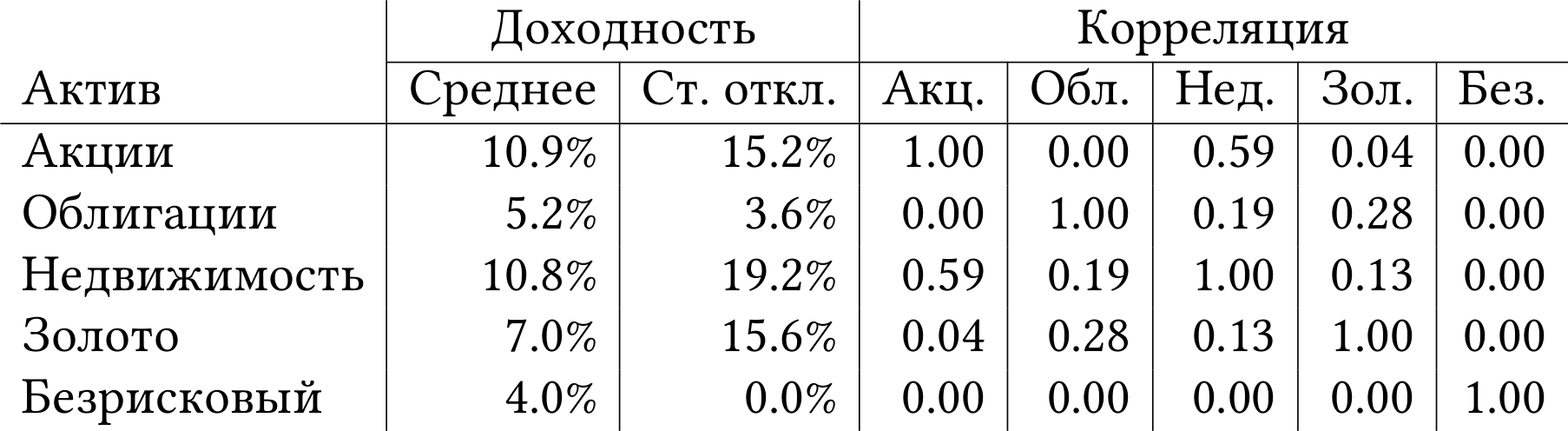
Таблица 2.1: Задача оптимизации портфеля из таблицы 1.4, дополненная безрисковым активом.
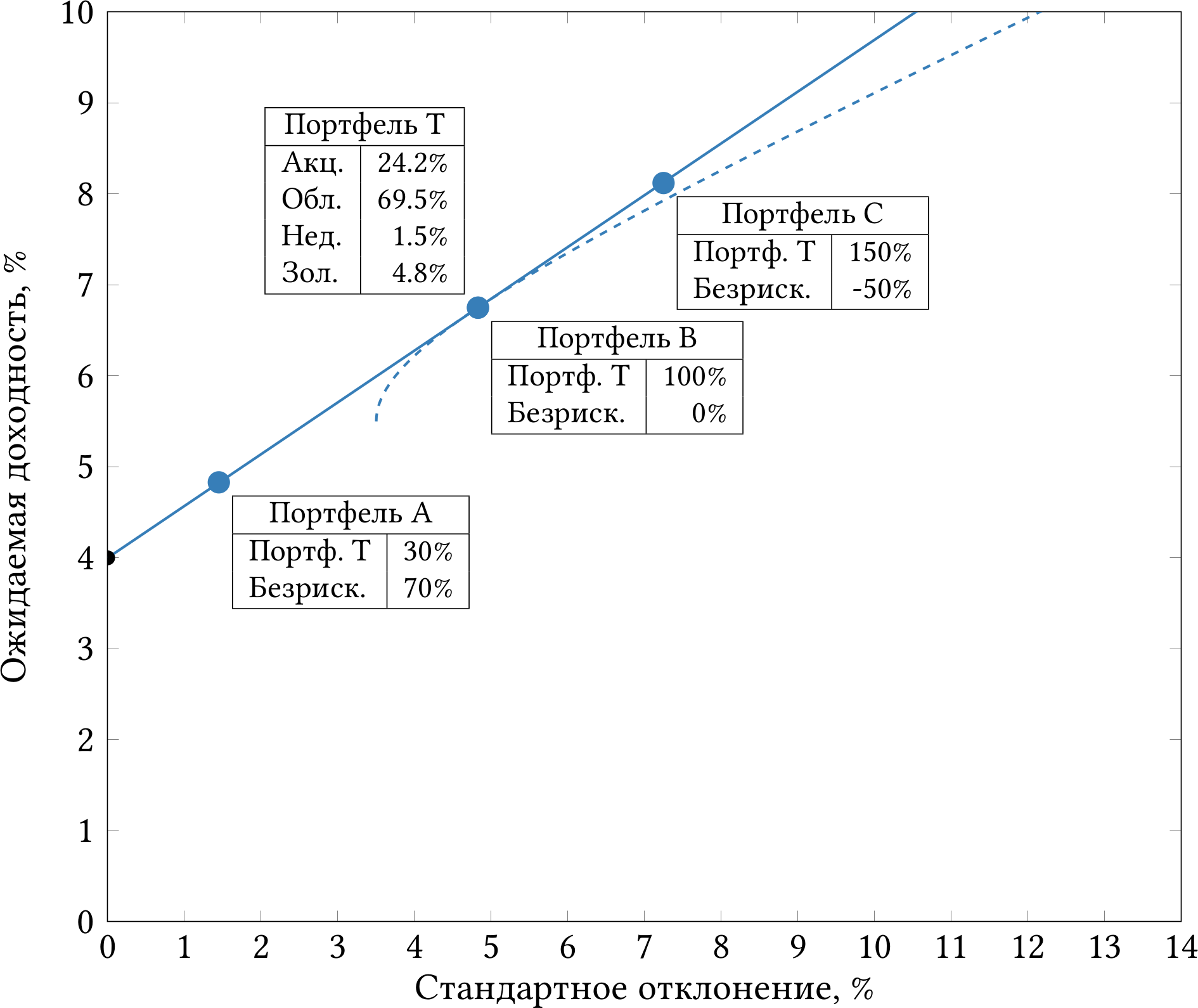
Рис. 2.1: Граница эффективности для портфелей, составленных из акций, облигаций, недвижимости, золота и безрискового актива.
Сплошная синяя линия — это новая граница эффективности для портфелей из четырёх рискованных активов и безрискового актива. Пунктирная линия — это старая граница эффективности с рисунка 1.3 для портфелей из четырёх рискованных активов. Можно строго математически доказать несколько фактов об этих двух линиях.
Во-первых, новая и старая граница касаются ровно в одной точке. Портфель T, который соответствует этой точке, так и называется — касательным (tangent). Этот портфель состоит из всех рискованных активов, которые у нас были раньше, но не содержит безрисковый актив.
Во-вторых, граница эффективности с безрисковым активом — прямая линия. Любой портфель на этой границе можно представить как комбинацию безрискового актива и касательного портфеля.
Например, инвестор может вложить 70% своего капитала в безрисковый актив, а 30% — в касательный портфель (то есть распределить 30% между четырьмя рискованными активами пропорционально их весам в касательном портфеле). Тогда у него получится портфель A, который лежит на границе эффективности и имеет стандартное отклонение 1.5% при ожидаемой доходности 4.8%.
Ранее мы щедро предоставили инвестору опцию занять деньги под безрисковую процентную ставку. Предположим, что инвестор займёт сумму, равную половине своего начального капитала, а затем вложит всё (и свои деньги, и заёмные) в касательный портфель. Тогда он окажется в точке C, которая лежит выше старой границы эффективности и была бы для него недоступна, если бы он не мог занимать деньги.
Выбирая пропорцию между безрисковым активом и касательным портфелем рискованных активов, инвестор может гулять по прямой границе эффективности. Увеличиваем долю безрискового актива — спускаемся влево в зону меньшей доходности и меньшего риска. Уменьшаем долю безрискового актива (или даже занимаем деньги) — поднимаемся вправо к более высокому риску и ожидаемой доходности.
На рынке может быть множество инвесторов, каждый со своей индивидуальной чувствительностью к риску. Предположим, что они все согласны по поводу ожидаемой будущей доходности активов и решают одну и ту же задачу оптимизации из таблицы 2.1. Поскольку они скармливают алгоритму оптимизации одни и те же входные параметры, то они получают один и тот же ответ — прямую границу эффективности с рисунка 2.1. Дальше каждый выбирает комфортное лично ему сочетание риска и доходности, то есть точку на общей прямой. Но никто не захочет оказаться под прямой, так как тогда он будет получать меньший доход за тот же риск или страдать от большего риска при том же доходе.
Следовательно, портфели всех инвесторов будут состоять из безрискового актива и из касательного портфеля. Никто не захочет держать комбинацию рискованных активов, отличную от касательного портфеля, потому что тогда он точно окажется под границей эффективности!
Предположим, что всего на рынке миллион инвесторов, и все вместе они должны инвестировать $200 миллиардов. Допустим, что в сумме все инвесторы вложили $100 миллиардов в безрисковый актив. Оставшиеся $100 миллиардов они распределят между рискованными активами. Но если каждый инвестор знает, что касательный портфель состоит из 24.2% акций, 69.5% облигаций, 1.5% фондов недвижимости и 4.8% золота, то как будут распределены эти $100 миллиардов? Очень просто: $24.2 миллиарда уйдут в акции, $69.5 миллиарда — в облигации, $1.5 миллиарда — в недвижимость, $4.8 миллиарда — в золото.
Хорошо, инвесторы сообща купили золота на $4.8 миллиарда. Сколько золота они купили? Да всё, что есть на рынке! В конце концов, ни один слиток не может остаться бесхозным (если вы знаете, где водятся бесхозные слитки золота, напишите мне!). Если инвесторы готовы вложить в золото $4.8 миллиарда, а всего в природе существует 4.8 миллиона унций золота, то невидимая рука рынка сделает так, что одна унция будет стоить ровно $1 000, ни центом больше, ни центом меньше.
Другими словами, все инвесторы сообща владеют всеми рискованными активами, доступными на рынке, этаким одним огромным касательным портфелем на всех. Именно поэтому касательный портфель ещё называют рыночным портфелем (market portfolio).
Это наблюдение значительно упрощает выбор оптимального портфеля. Единственное решение, которое вам нужно принять — как распределить деньги между безрисковым активом и рискованным касательным портфелем, то есть выбрать одну из точек на прямой границе эффективности. Только это решение зависит от ваших личных предпочтений между риском и доходностью.
Когда вы определились с желаемой долей инвестиций в рискованные активы, вам нужно как по списку в магазине купить все рискованные активы пропорционально их рыночной капитализации. Если все акции Google в природе стоят триллион долларов, а все акции Tesla стоят 400 миллиардов, то и в вашем личном касательном портфеле, и в общем касательном портфеле всех инвесторов Google и Tesla будут представлены в пропорции 10:4. Если же вы отклонитесь от рыночной пропорции, то у вас не получится составить касательный портфель, и вы окажетесь ниже границы эффективности.
Модель оценки капитальных активов (CAPM)
Обозначим доходность безрискового актива Rfree, доходность рыночного касательного портфеля Rmkt, её стандартное отклонение σmkt. Инвестор вложил долю β своего капитала в рыночный портфель, а долю 1 − β в безрисковый актив. Какую доходность R он получит?
Будущие доходности рынка Rmkt и портфеля инвестора R — это случайные величины. Перейдём к математическим ожиданиям:
Другими словами, ожидаемая избыточная доходность (excess return) сверх безрисковой процентной ставки прямо пропорциональна доле инвестиций в рыночный портфель β и ожидаемой избыточной доходности рыночного портфеля. Избыточную доходность рыночного портфеля ещё называют рыночной премией за риск (market risk premium).
В принципе, формула (2.1) не должна открыть вам Америку. Это всего-навсего уравнение прямой границы эффективности с рисунка 2.1. Ну да, чем больше денег вложишь в рискованный портфель, тем больше денег в среднем заработаешь. Что с того?
Так вот, можно строго доказать, что формула (2.1) описывает не только портфели на границе эффективности, а вообще все-все-все активы в экономике! Нужно только заменить коэффициент β на коэффициент, специфичный для конкретного актива. Обозначим Rasset доходность актива, σasset её стандартное отклонение, ρasset,mkt корреляцию с доходностью рыночного портфеля. Тогда справедлива следующая формула:
При этом «бета» актива βasset из формулы (2.2) равна
Формулы (2.2) и (2.3) называются моделью оценки капитальных активов (capital asset pricing model, CAPM). Авторами этой теоремы обычно указывают Уильяма Шарпа (William Sharpe) [Sha64], Джона Линтнера (John Lintner) [Lin65] и Яна Моссина (Jan Mossin) [Mos66].
Строгое доказательство можно посмотреть в книгах [Coc05, ch. 9.1] или [BKM14, ch. 9.1]. Идея доказательства в том, что если какой-то актив имеет более высокую доходность, чем предписано CAPM, то инвесторы будут стремиться добавить ещё немного этого актива в свои касательные портфели, чтобы улучшить соотношение риска и доходности. Выросший спрос подтолкнёт цену вверх, и будущая доходность уменьшится.
Что такое «бета» актива βasset? Проще всего объяснить на примере. Если «бета» актива равна 1.5, и весь рынок растёт (падает) на 1%, то при прочих равных актив растёт (падает) на 1.5%. Можно сказать, что «бета» отражает чувствительность актива к общему рыночному риску (market risk): насколько сильно актив растёт вместе с рынком в хорошие времена и насколько падает вместе с рынком в плохие.
CAPM говорит нам, что «бета» — единственное, что нам нужно знать об активе, чтобы понять, какой доходности от него ждать. Если «бета» акции равна 1.5, то нам не нужно анализировать финансовую отчётность компании или читать стенограммы выступлений гендиректора. Мы и так знаем, что если следующий год будет хорошим и рынок даст доходность 10% сверх безрисковой ставки, то акция даст избыточную доходность в среднем 15%. Нам нужно переживать не об ожидаемой доходности акции, а об ожидаемой доходности всего рынка.
Держу пари, что у вас остался вопрос: с какой это стати «бета» актива зависит от ковариации с рынком по формуле (2.3)? Почему более высокую ожидаемую доходность дают активы, которые имеют высокую корреляцию с рынком? Так вообще бывает?
Вспомните наш разговор в первой части о рациональных инвесторах с выпуклой вверх функцией полезности и пример с двумя акциями. Инвесторы ценят «защитные» активы, такие как облигации, которые почти не теряют в цене в плохие времена. Такие активы имеют «бету» около нуля и невысокую ожидаемую доходность, в полном соответствии с CAPM.
Активы с высокой «бетой», например акции, весело растут вместе с рынком в хорошие времена, когда у среднего инвестора и так всё неплохо, и стремительно падают вместе с рынком в кризис, когда средний инвестор рискует остаться без работы. Чтобы убедить инвестора купить такой актив, нужно пообещать ему дополнительную ожидаемую доходность (сделать скидку в цене). Снова CAPM даёт верное предсказание: чем сильнее связь с рынком, тем выше доходность, которую требуют инвесторы.
Систематический и идиосинкратический риск
CAPM (2.2), помимо всего прочего, даёт простой и понятный ответ на вечный вопрос инвесторов «как заработать?». Чтобы заработать что-то сверх безрисковой процентной ставки, нужно взять на себя риск и в среднем, на дистанции, заработать премию за этот риск. Любой ли риск вознаграждается премией (положительной ожидаемой доходностью)?
Например, с каждой акцией на рынке связан присущий именно этой акции специфический или, как его ещё называют, идиосинкратический (idiosyncratic) риск. Самолёт авиакомпании может разбиться, завод корпорации может сгореть, что приведёт к падению акций. Если вы владеете акциями авиакомпании, вознаграждает ли вас рынок за то, что вы несёте риск авиакатастрофы?
CAPM говорит «нет»! Не все йогурты одинаково полезны, не все риски одинаково вознаграждаются. Акции авиакомпании будут давать вам дополнительную ожидаемую доходность ровно в той степени, в какой акции авиакомпании связаны с рынком и общим состоянием экономики через коэффициент «бета».
По CAPM, вы зарабатываете премию только за тот риск, который реализуется в то же самое время, когда всему рынку плохо. Вряд ли вероятность падения самолёта возрастает в плохие времена, когда фондовый рынок падает. Если корреляция и есть, то она скорее отрицательная, потому что в кризис люди реже летают. А раз так, то у инвесторов нет причин требовать премию за этот идиосинкратический риск.
Если я вас не убедил, то подумайте вот о чём. Ни один рациональный инвестор в нашей модели не держит все инвестиции в одной акции. Вместо этого каждый инвестор покупает частичку касательного рыночного портфеля, в котором собраны сотни, тысячи, десятки тысяч акций и других активов. Весь идиосинкратический риск растворяется за счёт диверсификации. У какой-то компании дела могут случайно пойти лучше, у какой-то хуже, но в среднем эти отклонения от среднего будут компенсировать друг друга. Инвестора волнуют только те риски, которые могут разом ухудшить положение всех компаний в портфеле.
Риск, от которого нельзя избавиться диверсификацией, называется систематическим (systematic). Рыночный риск (риск того, что касательный рыночный портфель подешевеет) — как раз такой риск. Никакой диверсификацией вы не можете избавиться от риска того, что в экономике настанут тяжёлые времена (например, начнётся пандемия). Вы можете выбирать только «бету» своего портфеля, то есть насколько ваш личный портфель просядет в кризис вместе со всем рынком.
Если упростить всё до предела, то инвесторы зарабатывают премию только за тот риск, от которого нельзя избавиться. Если вы пришли в казино и играете в рулетку, то вы, безусловно, подвергаете свой капитал риску. Однако вы не обязаны нести этот риск и можете от него отказаться, если выйдете из-за стола. Поэтому в игре в рулетку есть риск, но нет премии за риск (точнее, из-за сектора зеро премия отрицательная). Точно так же, скорее всего, нет премии за риск в игре «угадай, чей самолёт упадёт следующим».
Если вы, в отличие от всех остальных инвесторов, держите в портфеле акции всего одной компании, то общий риск вашего портфеля разбивается на две компоненты: глобальный систематический риск и идиосинкратический риск одной компании. Вы зарабатываете дополнительную ожидаемую доходность только за систематическую компоненту. Весь идиосинкратический риск вы терпите бесплатно: вы чувствуете просадки портфеля (риск), но не получаете дополнительную ожидаемую доходность. CAPM говорит, что вам лучше было бы последовать примеру остальных инвесторов и диверсифицироваться, устранив тем самым идиосинкратический риск.
Рыночная премия за риск
Ещё раз посмотрим на уравнение CAPM (2.2). Ожидаемая избыточная доходность каждого актива (или портфеля активов) сверх безрисковой процентной ставки связана с ожидаемой избыточной доходностью рынка через коэффициент «бета». А чему вообще равна ожидаемая избыточная доходность рынка? Сколько процентов годовых рассчитывают заработать инвесторы, когда берут на себя рыночный риск?
Здесь есть методологическая проблема. Мы не можем залезть в голову инвесторам и проверить, на какую будущую рыночную премию за риск они закладываются сегодня, когда принимают решения о сделках. Мы можем только посчитать, какую премию за рыночный риск они зарабатывали в прошлом, и предположить, что в будущем ожидаемая доходность рыночного портфеля будет такой же, как раньше.
Есть ещё одна методологическая проблема. По CAPM, рыночный касательный портфель должен содержать вообще все-все-все активы в экономике, включая акции каждого ларька с мороженным. Понятно, что в реальности далеко не все активы являются торгуемыми, и мы можем посмотреть на исторические доходности только тех активов, которые обращались на открытом рынке. Мы не увидим доходности ларьков с мороженным, недвижимости, человеческого капитала.
Для практического применения CAPM обычно выбирают достаточно широкий индекс акций, такой как S&P 500 (500 крупнейших публичных компаний США) или MSCI World (1600 крупнейших компаний мира). Портфель акций с теми же весами, что и в индексе, торжественно объявляется «заместителем» (proxy) теоретического рыночного портфеля рискованных активов.
На рисунке 2.2 представлены историческая доходность рынка акций США с 1927-го года, доходность безрискового актива, разность между доходностью акций и безрисковой доходностью (рыночная премия за риск), а также инфляция.
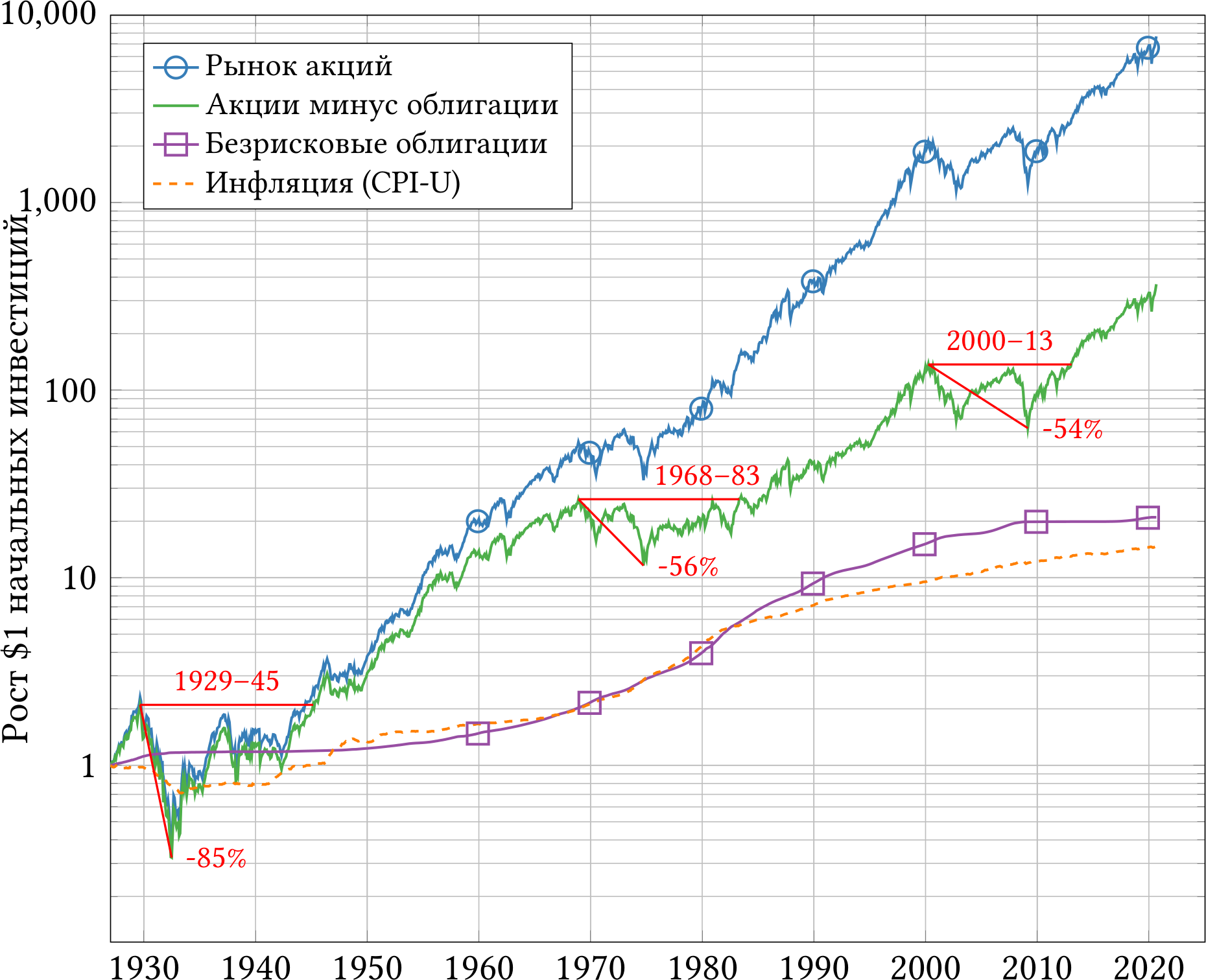
Рис. 2.2: Историческая доходность рынка акций США и безрисковых облигаций, инфляция. Данные: [Fre20], [Lab20].
Сделаем несколько очевидных наблюдений. Во-первых, на дистанции в 94 года рынок акций уверенно обогнал и безрисковую ставку, и инфляцию. Доллар, вложенный в акции в январе 1927-го года, то есть до краха 1929-го года и Великой депрессии, к августу 2020-го превратился в 7 682 доллара. С поправкой на инфляцию (за 94 года цены выросли в 14.7 раза), это 523 доллара образца 1927-го года.
Во-вторых, акции обгоняют безрисковую ставку и инфляцию только на дистанции нескольких десятков лет. История знает примеры, когда акции были хуже безрискового актива в течение 15-ти лет подряд. Как вам, например, перспектива вложиться в акции в 1968-м году и обогнать безрисковые облигации только к 1983-му году? Или, скажем, вложиться в акции в 1929-м, потерять 85% к 1932-му, а потом сидеть в убытках до конца Второй мировой войны?
Что ещё нужно сказать о доходности акций? За 94 года инвесторы в акции 28 раз (30%) оставались в минусе относительно безрисковой ставки по итогам года. 17 раз (18%) просадка составляла -10% или хуже. Три самых неудачных для акций года — 1931-й (-45%), 2008-й (-38%) и 1974-й (-36%). Лучше быть морально готовым к таким потерям, если вы принимаете решение инвестировать свои деньги в акции.
Чтобы добавить статье наукообразности, в таблице 2.2 я посчитал среднюю избыточную доходность акций сверх безрисковой ставки, её стандартное отклонение и 99% доверительный интервал. t-статистика из теста Стьюдента больше 4 и p-значение меньше 0.1% говорят нам, что было бы маловероятно увидеть такой рост акций в течение 94-х лет, если бы на самом деле ожидаемая избыточная доходность была равна нулю, а весь рост объяснялся бы счастливой случайностью.
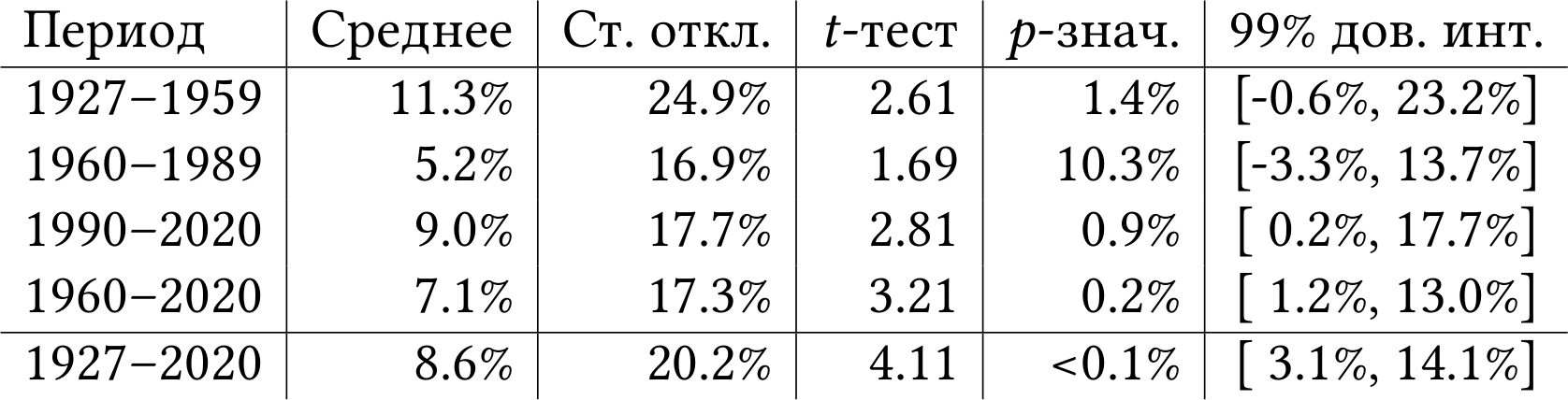
Таблица 2.2: Годовая избыточная доходность рынка акций США сверх безрисковой процентной ставки (рыночная премия за риск). 1927–2020. Данные: [Fre20].
Сделаем вывод, что в среднем рыночный портфель американских акций приносит инвесторам премию за риск 7%–9% годовых плюс-минус лапоть при стандартном отклонении примерно 20%. Такого порядка премию за риск можно включать в CAPM, чтобы оценить ожидаемую доходность активов.
Загадка рыночной премии за риск
Как мы выяснили, в среднем инвесторы зарабатывают премию за риск примерно 7–9% годовых, если они соглашаются взять на себя систематический рыночный риск. Не слишком ли много? Есть точка зрения, что это не согласуется со стандартными моделями избегания риска. Инвесторы должны очень-очень не любить риск, чтобы спрос и предложение уравновесились на такой высокой премии за риск (то есть на таких низких ценах).
Очень-очень — это сколько? Представьте, что вам предлагают сыграть в лотерею, которая с вероятностью 50/50 либо удвоит ваш капитал, либо уполовинит его. Вы можете заплатить фиксированную сумму и отказаться от игры. Сколько вы готовы заплатить? Согласно некоторым моделям, средний инвестор должен предпочесть наверняка заплатить 49% капитала, лишь бы не играть в лотерею, которая с вероятностью 50% отнимет у него 50% капитала. Только такая абсурдная нелюбовь к риску может объяснить ту рыночную премию за риск, которую мы наблюдаем.
Подозрительное расхождение теории с практикой, не так ли? Этот эффект даже получил собственное название — загадка рыночной премии за риск (equity risk premium puzzle). Как принято в экономической науке, экономисты придумали множество объяснений, как такое возможно. Если вам интересно, то можете почитать обзоры литературы [ST97] (покороче) и [Meh07] (подлиннее).
Согласно одной из гипотез, инвесторы опасаются риска крупной финансовой катастрофы или политической нестабильности, которая уничтожит рынок. За 200 лет такой катастрофы на рынке США не случилось, но это не означает, что она не может произойти в будущем. Легко привести примеры рынков акций, которые прекратили своё существование, как, например, рынок Российской империи.
Рынок США является одним из долгожителей и показывает хороший рост, поэтому неудивительно, что к нему приковано внимание инвесторов и исследователей. Возможно, мы упускаем из виду те рынки, которые не дожили до наших дней, и таким образом совершаем ошибку выжившего (survivorship bias).
Ещё одно объяснение, которое мне больше по душе, связано с особенностями поведения и неполной рациональностью людей. Чтобы проиллюстрировать его, я попрошу вас принять участие в небольшом мысленном эксперименте.
На рисунке 2.3 представлены возможные результаты инвестиций в два актива, A и B, в любой случайно взятый год. Всего возможны 50 равновероятных исходов, каждому их которых соответствует столбик на графике. Для вашего удобства я упорядочил сценарии на оси x по возрастанию доходности. Наихудший возможный сценарий — первый столбик на графике, а наилучший — пятидесятый. Если вы должны вложить всё своё состояние на 15 лет либо в актив A, либо в актив B, то какой актив вы выберете?
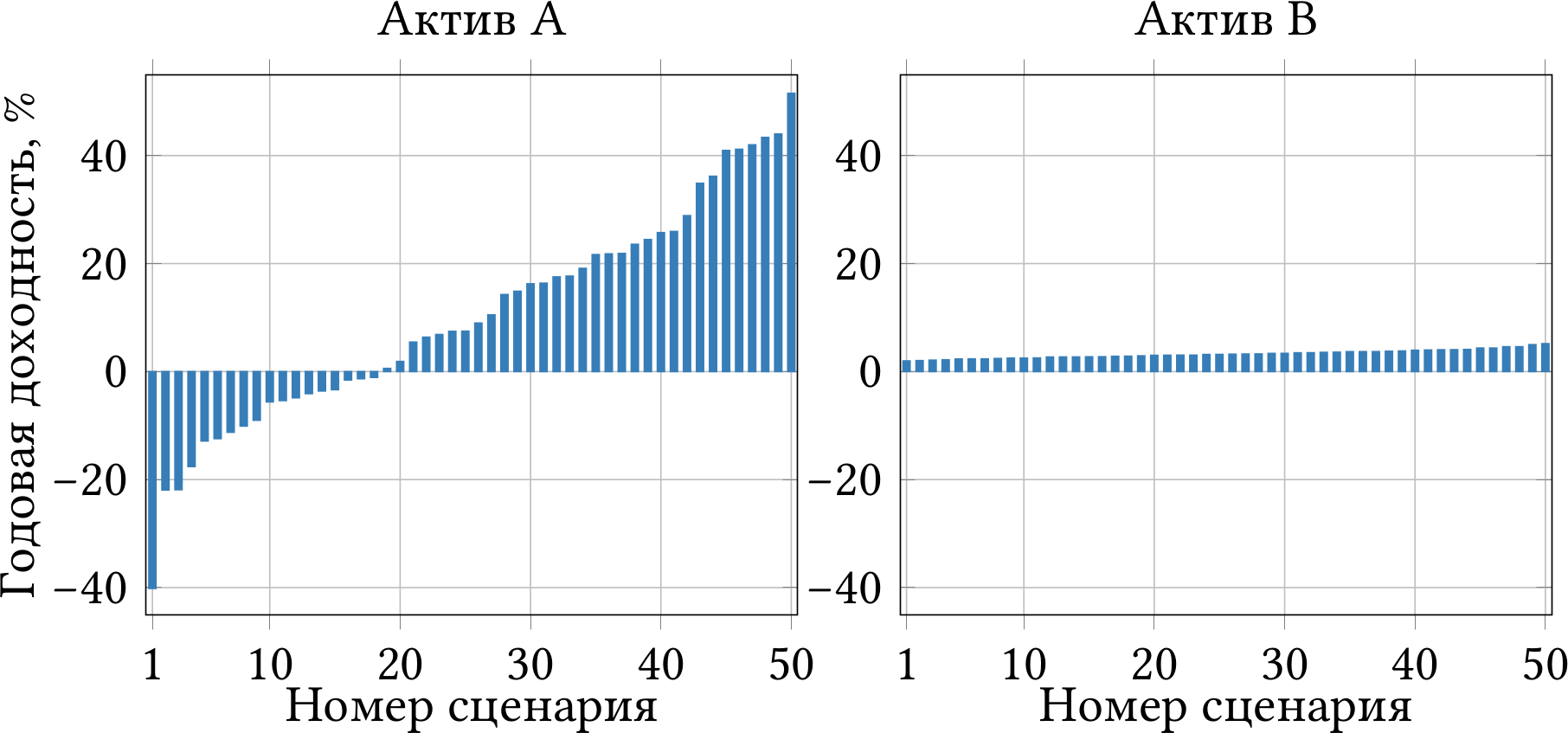
Рис. 2.3: Возможные результаты инвестиций в активы A и B. Инвестор должен выбрать один из двух активов.
Теперь обратите внимание на рисунок 2.4. Снова я предлагаю вам на выбор два актива, C и D, и 50 равновероятных сценариев. Снова вы должны вложить все деньги, какие у вас есть, либо в актив C, либо в актив D. Что вы предпочтёте на этот раз?
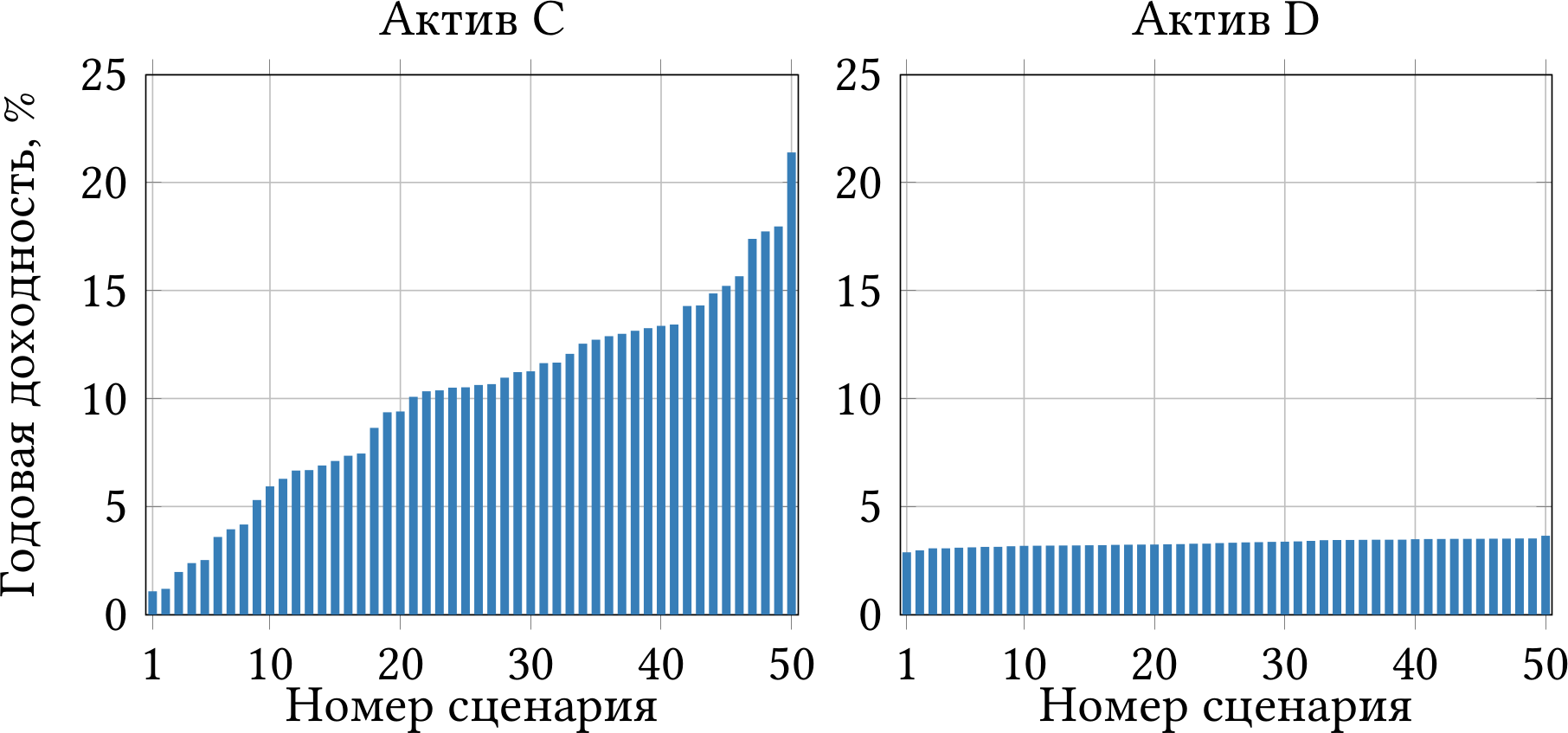
Рис. 2.4: Возможные результаты инвестиций в активы C и D. Инвестор должен выбрать один из двух активов.
Когда я проводил этот опрос среди студентов, три четверти выбрали актив B в первом случае и актив C во втором. Их можно понять. В 18-ти случаях из 50-ти актив A теряет в цене, причём можно потерять и 20%, и все 40%. Актив B, который не имеет таких просадок, выглядит привлекательнее. Актив C иногда тоже оказывается хуже актива D, но таких случаев немного, и даже в них актив С не опускается ниже нуля.
Подвох в том, что A и C — это один и тот же актив, рынок акций США. Активы B и D — тоже один и тот же актив, безрисковые облигации. Всё отличие во временном горизонте. На рисунке 2.3 приведены 50 случайных доходностей за один наудачу взятый год, а на рисунке 2.4 — 50 доходностей за выбранные наудачу 15 лет подряд.
Другими словами, если вы 15 лет подряд будете вкладываться в актив A, то получите доходность как у актива C. В среднем, рынок акций растёт, поэтому случайные падения на 20% и даже на 40% в неудачный год компенсируются высокой доходностью в другие года. На дистанции 15 лет у вас не так много шансов оказаться в минусе, даже если по дороге вы переживёте падение на 40%.
Судя по всему, эволюция не выработала у нас способность быстро складывать в уме много случайных величин и понимать распределение их суммы. Поэтому мы механически переносим результат одного года на результат 15-ти лет подряд и можем совершить ошибку. Ричард Талер (Richard Thaler) называет эту особенность поведения людей близоруким избеганием риска (myopic risk aversion) [BT95].
Из этого следует интересный практический вывод. Чем реже вы интересуетесь промежуточными результатами своих инвестиций и проверяете состояние счёта, тем более рискованный (и доходный) портфель вы можете себе позволить [Tha15, ch. 20].
Как мы выяснили, рынок акций даёт премию в среднем 8.6% в год при стандартном отклонении 20.2%. Давайте пересчитаем годовые доходности в дневные, полагая, что в году 250 торговых дней. Получится, что в среднем рынок растёт на 8.6% ∕ 250 ≈ 0.03% за торговый день при стандартном отклонении 20.2% ∕ sqrt(250) ≈ 1.28%. Это означает, что на горизонте одного дня рост рынка почти незаметен, а вот дневные колебания могут быть весьма ощутимыми. Например, дневная просадка на 2% — это всего-навсего 2% ∕ 1.28% ≈ 1.56 стандартных отклонения. Даже если доходности распределены нормально, то потери 2% или хуже будут случаться с вероятностью 5.9%, то есть раз в 17 торговых дней.
Если вы хотите инвестировать деньги на пенсию на горизонте 20 лет, то лучшее, что вы можете сделать — это вложить деньги в акции, закрыть торговый терминал и снести его с компьютера. Желательно также не смотреть телеканалы с финансовой аналитикой, а на новостных сайтах читать только спортивный раздел. Через 20 лет в день выхода на пенсию вы, скорее всего, увидите на счёте хороший «плюс».
Если же вы, как и многие начинающие инвесторы, будете проверять состояние счёта каждый день или, ещё хуже, каждый час, а по ночам будете просыпаться, чтобы полистать новости, то ваше душевное равновесие будет под угрозой. Есть вероятность, что тот чувствительный орган, которым все инвесторы ощущают просадки портфеля, не выдержит постоянных колебаний на несколько процентов вверх и вниз, и вам придётся перебалансировать свой портфель в сторону уменьшения риска и доходности.
Предсказание рыночной премии за риск
Можно ли заранее угадать, вырастет ли рынок акций в следующем году или упадёт? Если бы мы знали ответ на этот вопрос, то мы могли бы в хорошие времена инвестировать деньги в акции, а перед плохими временами продавать акции и пережидать кризис в безрисковых облигациях.
Предсказание будущей доходности рынка акций — это Святой Грааль финансов, наряду с предсказанием будущих курсов валют. Как вы понимаете, многие хотели бы владеть этим секретом. К сожалению, я должен вас разочаровать. Не похоже, чтобы какой-то индикатор (или группа индикаторов) предсказывали бы будущую доходность рынка акций лучше, чем простой прогноз «в следующем году будет так же, как в среднем в истории» [WG08].
В частности, любимые многими аналитиками дроби «что-то на что-то», такие как дивиденды к цене (dividend/price, D/P), цена к прибыли (price/earnings, P/E), капитализация рынка к ВВП (market cap/GDP) и другие, не помогают предсказать, какой будет рыночная премия за риск в следующем году.
За последние годы я видел немало графиков отношения P/E. Аналитики, которые их показывали, заявляли, что отношение P/E близко к историческому максимуму, и поэтому «скоро» мы увидим обвал рынка. Наступил март 2020-го года, и обвал рынка на 35%, которого все так ждали, случился. Как вы считаете, обвал случился из-за пандемии коронавируса или из-за высокого отношения P/E?
Я не могу запретить аналитикам строить графики, «предсказывающие» обвал рынка. Если вы хотите понять, стоит ли им верить, то проверьте по крайне мере две вещи.
Во-первых, предсказание должно пройти бэктестинг (backtesting) вне выборки (out of sample). Грубо говоря, мы должны сыграть в следующую игру. Предположим, что мы перенеслись в 1 января 1989 года и знаем всю информацию, известную к этой дате. Мы скармливаем эту информацию нашему алгоритму-предсказателю, и он говорит, что в 1989-м году рынок акций даст доходность -10%. А что на самом деле произошло в 1989-м? Рынок вырос на 20.5%. Что ж, ошибочка вышла, запишем.
Переносимся в 1 января 1990 года и повторяем процедуру. Скармливаем алгоритму всю информацию, известную к 1 января 1990 года, получаем прогноз -10%, сравниваем с реальным результатом рынка −14% и радуемся, что попали точно. Проделав эту процедуру много раз, мы должны проверить, что алгоритм предсказывает доходность рынка статистически значимо лучше, чем простое предсказание «доходность в год N будет равна средней доходности за годы с N-30 по N-1».
Во-вторых, крайне желательно, чтобы за предсказанием стояла какая-то модель, которая объясняет, почему этот индикатор работает. Почему высокое отношение P/E увеличивает вероятность обвала рынка? Под моделью я понимаю что-то похожее на мои рассуждения про рациональных инвесторов в начале статьи. Вот наша экономика, в ней вот такие люди, с такими-то правилами поведения, с такими-то целями и доступными рыночными инструментами. Дальше несколько страниц математических выкладок и вывод: в нашей модели P/E предсказывает обвалы рынка и, кстати, это подтверждается историческими данными.
Моё к отношение к этому вопросу близко к фатализму. Аналитики правы в одном: обвал действительно будет. Обвалы рынка акций неизбежны так же, как снег зимой. Другое дело, что наука пока не может предсказать, будет ли идти снег в наперёд заданный день января, если сейчас на календаре август. Точно так же мы можем быть уверены, что нам предстоит пережить ещё не один обвал рынка, но мы не в силах предсказать, когда он случится.
Собственно, периодические обвалы — это именно тот риск, за который инвесторы в акции и зарабатывают премию за риск в хорошие времена. Если бы все могли легко избежать этого риска, то и премии за риск бы не было.
На мой взгляд, частному инвестору лучше не играть в угадайку, а определиться с приемлемым уровнем риска и вложить в рискованные акции соответствующую долю капитала. Предположим, что вы можете пережить потерю 20% капитала без последствий для здоровья, а худшая возможная просадка рынка акций составляет 80%. Тогда вам стоит вложить в акции 20% ∕ 80% = 25% капитала и спать спокойно, а поиски Святого Грааля оставить профессионалам.
Отношения Шарпа и Сортино. Геометрическое среднее
Раз уж мы заговорили о профессионалах, давайте рассмотрим парочку метрик, которые широко используются в индустрии для оценки соотношения риска и доходности.
Первая метрика — отношение Шарпа (Sharpe ratio). Идея достаточно простая: давайте разделим доходность сверх безрисковой ставки на риск, измеренный как стандартное отклонение. Чем выше доходность и чем меньше стандартное отклонение, тем лучше баланс риска и доходности.
Обычно отношение Шарпа считают на основе временных рядов прошлой доходности. Пусть у нас есть n периодов (месяцев, лет). Обозначим Rt доходность инвестиций в период t, а доходность безрискового актива обозначим Rfree,t. Тогда отношение Шарпа вычисляется по формуле
В числителе дроби (2.4) стоит средняя избыточная доходность за n периодов, а в знаменателе — выборочное стандартное отклонение.
Хозяйке на заметку: касательный портфель имеет максимальное отношение Шарпа среди всех портфелей, составленных из рискованных активов. В рамках CAPM этот же портфель является рыночным портфелем всех рискованных активов. Поэтому CAPM можно интерпретировать ещё и так: вы не можете получить лучшее отношение Шарпа (лучший баланс риска и доходности), чем в диверсифицированном рыночном портфеле.
Отношение Шарпа измеряет риск стандартным отклонением. В формуле выборочного стандартного отклонения одинаково учитываются неожиданные отклонения от средней доходности R вверх и вниз. Между тем, большинство инвесторов ничего не имеют против случайных всплесков необычно высокой доходности, но очень переживают, когда доходность оказывается хуже ожиданий.
Чтобы учесть эту особенность, можно использовать отношение Сортино (Sortino ratio). Для этого нам понадобится дополнительный параметр — минимально приемлемая доходность (minimum acceptable return, MAR) Rmin,t. Этот уровень доходности может быть как константой (например, 0%), так и переменной величиной (например, безрисковой ставкой Rfree,t).
В числителе дроби (2.5) стоит средняя доходность сверх минимально приемлемой, а в знаменателе — так называемое стандартное отклонение «вниз», которое учитывает только те доходности, которые оказались хуже, чем минимально приемлемая.
Как видите, оба отношения устроены похожим образом. В числителе какая-то мера доходности, в знаменателе какая-то мера риска. Я не буду вас утомлять перечислением других похожих метрик, потому что думаю, что общий принцип уже должен быть понятен.
Есть ещё одна полезная метрика, которая может быть очень важна для долгосрочных инвесторов — геометрическое среднее доходности. Арифметическое среднее (например, как в таблице 2.2) является лучшей статистической оценкой доходности в один случайный год. Если вас интересует доходность за много лет подряд, то вам нужно учитывать капитализацию процентов.
Рассмотрим пример. Пусть мы знаем, что с вероятностью 50/50 рынок либо растёт на 20%, либо падает на 20%. Вы вложились в рынок на 20 лет, и 10 раз за эти 20 лет рынок вырос на 20%, а 10 раз упал на 20%. Чему равно арифметическое среднее доходности? Конечно же, нулю, потому что 10 ⋅ 20% + 10 ⋅ (−20%) = 0%. Но означает ли это, что вы получили доходность ноль, то есть остались с тем же капиталом, с которого начинали?
Разумеется, нет! Из-за капитализации процентов сходить вверх на 20% и вниз на 20% не означает остаться при своих. Если у вас было 100 рублей, то после роста на 20% у вас окажется 120 рублей. Падение на 20% заберёт у вас 120 ⋅ 0.2 = 24 рубля, и у вас останется только 96. Если эти горки повторятся 10 раз, то у вас останется всего 100 ⋅ (1 + 0.2)10 ⋅ (1 − 0.2)10 ≈ 66 рублей. Сложный процент съест треть вашего капитала несмотря на то, что средняя арифметическая доходность — 0%.
Для инвестиций на длинные горизонты разумно использовать геометрическое среднее, которое учитывает капитализацию процентов. Формула будет выглядеть так:
В таблице 2.3 я посчитал отношение Шарпа, отношение Сортино и геометрически среднюю годовую доходность для американского рынка акций.
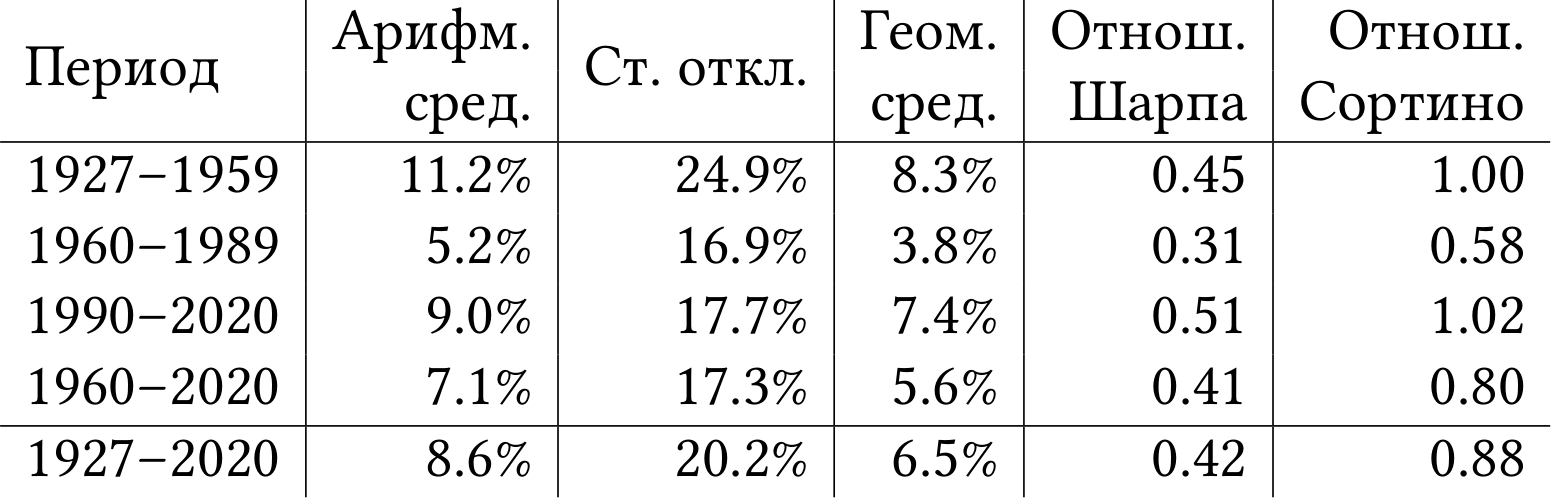
Таблица 2.3: Годовая избыточная доходность рынка акций США сверх безрисковой процентной ставки (рыночная премия за риск). 1927–2020. Данные: [Fre20].
Можно сделать как минимум два практических вывода. Во-первых, на длинной дистанции доходность с учётом капитализации процентов на целых 2 процентных пункта ниже, чем арифметическое среднее (6.5% против 8.6%). Это всё равно довольно много, потому что удвоение покупательной способности инвестиций (ведь мы считаем рост сверх безрисковой ставки) происходит каждые 11 лет.
Во-вторых, отношение Шарпа рынка акций — примерно 0.42. Если на коктейльной вечеринке с вами пытается познакомиться трейдер, который вам неприятен, то спросите, какой у него Шарп. Если 0.5 или меньше, то скажите, что это сравнимо с индексом акций, и тогда он обидится и уйдёт. А вот если больше 1.0, то преодолейте неприязнь, поддержите разговор и выведайте подробности.
Отказ от ответственности
Мнение автора статьи может не совпадать с официальной позицией Deutsche Bank AG. Статья не является предложением или рекламой какой-либо услуги. Упоминание третьих сторон не предполагает одобрения или неодобрения. Автор и Deutsche Bank напоминают, что торговля на финансовых рынках сопряжена с риском, и не несут ответственности за возможные негативные последствия ваших личных инвестиционных решений.
Список литературы
[BKM14] Zvi Bodie, Alex Kane, and Alan J Marcus. Investments. 4th ed. McGraw-Hill Education, 2014. ISBN: 978-0-07-786167-4.
[BT95] Shlomo Benartzi and Richard H Thaler. “Myopic loss aversion and the equity premium puzzle”. In: The quarterly journal of Economics 110.1 (1995), pp. 73–92.
[Coc05] John H Cochrane. Asset pricing. Revised edition. Princeton University Press, 2005. ISBN: 0691121370.
[Fre20] Kenneth R French. Kenneth French Data Library. 2020.
[Lab20] U.S. Bureau of Labor Statistics. Consumer Price Index for All Urban Consumers: All Items in U.S. City Average [CPIAUCNS]. 2020.
[Lin65] John Lintner. “The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets”. In: The Review of Economics and Statistics 47.1 (1965), pp. 13–37.
[Mar11] Donald Marron. “The Day the United States Defaulted on Treasury Bills”. In: Forbes (May 2011).
[Meh07] Rajnish Mehra. The equity premium puzzle: A review. Now Publishers Inc, 2007.
[Mos66] Jan Mossin. “Equilibrium in a capital asset market”. In: Econometrica: Journal of the econometric society (1966), pp. 768–783.
[Sha64] William F Sharpe. “Capital asset prices: A theory of market equilibrium under conditions of risk”. In: The Journal of Finance 19.3 (1964), pp. 425–442.
[ST97] Jeremy J Siegel and Richard H Thaler. “Anomalies: The equity premium puzzle”. In: Journal of Economic Perspectives 11.1 (1997), pp. 191–200.
[Tha15] Richard H Thaler. Misbehaving: The making of behavioral economics. W. W. Norton & Company, Inc, 2015. ISBN: 978-0-393-08094-0.
[WG08] Ivo Welch and Amit Goyal. “A comprehensive look at the empirical performance of equity premium prediction”. In: The Review of Financial Studies 21.4 (2008), pp. 1455–1508.
Все статьи цикла
Часть 1. Рациональные инвесторы. Риск и доходность. Диверсификация. Портфельная оптимизация
Часть 2. Модель CAPM. Систематический и идиосинкратический риск. Рыночная премия за риск
Часть 3. Анализ доходности фондов. Факторные модели. Арбитражная теория ценообразования
Часть 4. Биржевые фонды. Эффективность рынка. Личный опыт и сбережения на пенсию


