Натолкнулся в Интернете на задачу, которая называется «Теорема о четырех красках».
Вот ее страница в Википедии. Если не знаете эту задачу, то прочтите — интересная история.
Сама задача звучит так: сколько минимум нужно красок, чтобы раскрасить государства на карте, и при этом чтобы все граничащие территории имели разный цвет?
Многократные попытки решить эту задачу в течение последних ста лет интригуют, а итоговое ее решение исключительно благодаря компьютерам и некоему «специальному программному обеспечению» звучит как-то не очень убедительно. Поэтому попробуем разобраться самостоятельно.
Приступим.
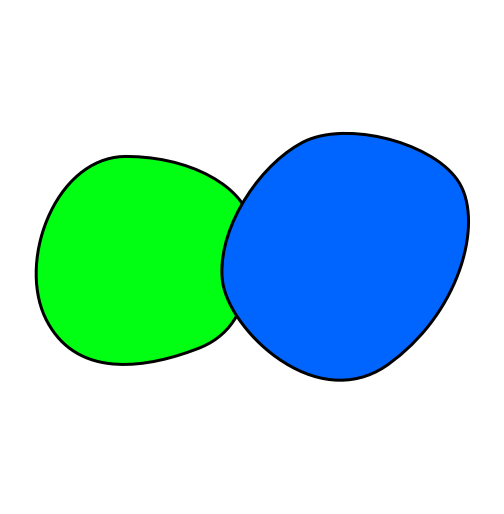

Как видим, одновременно два граничащих государства (рис.1) требуют два, а три граничащих государства (рис.2) — три разных цвета.

В случае с одновременно четырьмя граничащими государствами (рис.3) потребуется четыре цвета.
И на этом рост количества цветов заканчивается, а пятый цвет уже не понадобится. Почему так?
Потому что когда одновременно граничат четыре государства, то одно из них обязательно оказывается полностью окружено тремя другими и больше ни с чем уже граничить не может. Его цвет высвобождается для дальнейшего использования, а продолжение окрашивания возвращается к предыдущему шагу с тремя одновременно граничащими государствами (рис.4).

Разберем этот момент подробнее и покажем, почему в случае с четырьмя одновременно граничащими государствами одно из них всегда оказывается изолированным от всех остальных, что высвобождает его цвет для последующего шага окрашивания.


Для большей наглядности заменим государства точками, а их пограничные контакты обозначим соединяющими точки линиями (рис.5). Посмотрим, почему справедливо утверждение, что при одновременном соединении всех четырех точек одна из них обязательно окажется внутри трех других (рис.6).

Пусть исходно (рис.7) у нас есть три соединенных точки (точки 1, 2 и 3). Будем присоединять к ним четвертую точку (точку 4).


Соединив точку 4 с точками 1 и 2, нам остается соединить ее с точкой 3. Сделать это можно либо с одной стороны (a), либо с другой стороны (b). А такое соединение делает внутренней одну из двух точек (точку 1 на рис.8 или точку 2 на рис.9). Поэтому одновременное соединение четырех точек обязательно приводит к изоляции как минимум одной из них.
В контексте нашей задачи это означает, что при одновременном контакте четырех граничащих государств требуется четыре цвета, но при этом один из цветов становится внутренним и высвобождается для следующего шага раскрашивания. Поэтому пятый цвет не потребуется.
Более того, из изоляции одной из точек уже при четырех цветах также следует, что невозможно существование одновременно пяти граничащих государств.
Как и авторам решения этой головоломки из вышеуказанной статьи в Википедии, нам для решения этой задачи также потребовалась современная компьютерная техника и специальное программное обеспечение: мне — для того, чтобы написать этот текст, а вам — чтобы прочитать его.


