Что такое суперсимметрия?
Суперсимметрия – это гипотетическая симметрия пространства и времени, причём уникальная. Среди физиков-теоретиков эта идея несколько десятилетий была очень популярной по ряду причин – она была хитом, когда я был студентом, ещё до того, как физика стала крутой темой, и даже ещё раньше.
Автоматическим следствием наличия в природе симметрии будет то, что у каждого типа частиц будет один или несколько суперпартнёров – другой тип частиц, обладающий теми же свойствами, но отличающийся определённым, и важным, образом. Если частица – фермион, то её суперпартнёр – бозон. Если частица – бозон, её суперпартнёр – фермион (что такое фермионы и бозоны).
В нашем мире множество фермионов – это все частицы материи – и множество бозонов – это все переносчики взаимодействий. Но ни у одной из этих частиц нет свойств, подходящих для того, чтобы быть кому-то суперпартнёром. Поэтому, если бы суперсимметрия была природной симметрией, у каждого из известных нам типов элементарных частиц должны были бы быть партнёры, пока нами не открытые. А поскольку нам известно более 20 частиц, то работы у нас непочатый край!
Так что же это за симметрия? Это симметрия, связывающая пространство и время с направлениями пространства и времени суперпартнёров – иначе говоря, у пространства-времени имеются дополнительные измерения, непохожие на знакомые нам. В бозонном измерении – к ним мы привыкли – можно двигаться сколько угодно далеко, допустим, шаг за шагом продвигаться влево. В фермионном измерении всё устроено так, что можно сделать только один шаг. Если сделать ещё один шаг, то вы окажетесь нигде. Вы можете только вернуться. Это звучит странно, и это так и есть; в итоге приходится определять такие измерения через математику, а не при помощи слов или аналогий.
Теория относительности Эйнштейна прекрасно справляется с описанием и предсказанием множества аспектов нашего мира. Его теория состоит из набора уравнению, подчиняющихся определённому набору симметрий. К примеру – трансляционная симметрия, или симметрия, связанная с переносом эксперимента из одного места пространства-времени в другое: эксперимент, проведённый сегодня в Лондоне, даст такой же результат, как тот же самый эксперимент, проведённый через несколько месяцев в Токио. В 1960-х математически было доказано, что суперсимметрия – это единственная симметрия, которую можно добавить к симметриям теории Эйнштейна так, чтобы получившиеся уравнения не стали расходиться со свойствами реального мира. В этом смысле суперсимметрия стоит особняком.
Где же эти частицы-суперпартнёры?
Если бы суперссиметрия была точной симметрией природы, мы бы уже нашли множество суперпартнёров.
Перед тем, как следовать далее, давайте вспомним, какие нам известны элементарные частицы. В статье по ссылке рис. 1 и 2 особенно полезны для того, чтобы охватить одним взглядом частицы и сравнить их с рисунками, приведёнными ниже.
На рис. 1 я показал, какие частицы существовали бы в мире, если бы Стандартная Модель была дополнена точной суперсимметрией.
• Для каждого фермиона материи, например, электрона или странного кварка, есть две новые частицы – обе бозоны. Имена у них довольно уродливые, сэлектрон и странный скварк, где «с» означает суперсимметрию. Вы можете спросить, почему их по две (и почему для каждого нейтрино всего по одной). Обратитесь к рис. 3 ниже, и вам должно всё стать понятно.
• Для бозонов-переносчиков взаимодействий имеются партнёры-фермионы. У фотона есть фотино, у глюонов – глюино, и т.д. С массивными W-бозонами всё чуть сложнее. У них есть партнёр вино [wino], а также партнёр Хиггс, по имени H+ (Внимание! Эту частицу нельзя путать с частицей H+, появляющейся в статье, в которой рассказывается, что было бы со Стандартной Моделью, если бы поле Хиггса было нулевым. К сожалению, в физике частиц с именованием частиц есть постоянная проблема – букв не хватает). У всех этих частиц точно такая же масса, в этом воображаемом суперсимметричном мире.
• В этой модели есть две частицы Хиггса, h0 и H0, и у каждой есть партнёр хиггсино. Одна безмассовая, вторая массивная. Почему две? Оказывается, в суперсимметричном мире необходимо наличие двух частиц для того, чтобы у верхних и нижних кварков масса появлялась обычным способом. Второй аргумент – два хиггсино необходимы для математической непротиворечивости.
Но, очевидно, что этот идеально суперсимметричный мир – не наш. Как показано на рисунке, в таком мире частицы и их суперпартнёры:
• Точно так же взаимодействуют с другими частицами и их суперпартнёрами.
• Обладают точно такой же массой.
Мы бы уже более ста лет назад знали о существовании частиц, у которых был бы такой же электрический заряд и такая же масса, как у электронов, но при этом они бы электронами не являлись. Например, у нас были бы атомы с электронами, атомы с сэлектронами, и атомы с их смесью. Количество типов атомов было бы намного большим наблюдаемого, и поскольку бозоны в атомах вели бы себя совершенно не так, как фермионы, химия новых атомов была бы совершенно другой. Данные и повседневный опыт исключают эту возможность. Нет никаких сэлектронов с массой электронов, и точка. Так что точная суперсимметрия не является корректной теорией природы, и мы это знали ещё до того, как её задумывали.
Конец суперсимметрии? Не так быстро.
Несмотря на кажущуюся катастрофу, изначальная теория суперсимметрии даёт нам простой и правдоподобный выход из ситуации. В физике распространена идея о том, что симметрии могут быть спрятаны от нашего взора (физики говорят, спонтанно нарушаться, но это не очень хороший интуитивный пример – симметрия есть, её просто сложно распознать).

Рис. 2
Один из примеров – вращательная симметрия на Земле. Законы природы не зависят от того, каким образом будет ориентирован эксперимент (см. рис. 2). Это так и есть, но это сложно увидеть на Земле, где имеет значение, повёрнут ли ваш эксперимент нужной стороной вверх, или он находится вверх ногами, или он наклонён. Но в далёком космосе, далеко от планет, лун и звёзд, законы природы обладают вращательной симметрией. Ваш эксперимент даст один и тот же ответ вне зависимости от его ориентации. Кстати, измерения света, испущенного очень удалёнными атомами, подтверждают эту теорию. Земля нас запутывает. Она заставляет нас думать, что направление вниз отличается от направления вверх или влево. Но это явное различие не является свойством законов природы. Различие возникает из-за близости Земли, прячущей от нашего взора вращательную симметрию.
Вопрос в том, что если какой-то аспект нашего мира (не такой грубый, как Земля, но какой-нибудь незаметный, вроде поля Хиггса) прячет от нашего взора суперсимметрию по всей Вселенной? Что тогда? Оказывается, что довольно легко получить такой же мир, как наш, где суперпартнёры известных части существуют, просто стали тяжелее – слишком тяжёлыми для того, чтобы мы обнаружили их в экспериментах.
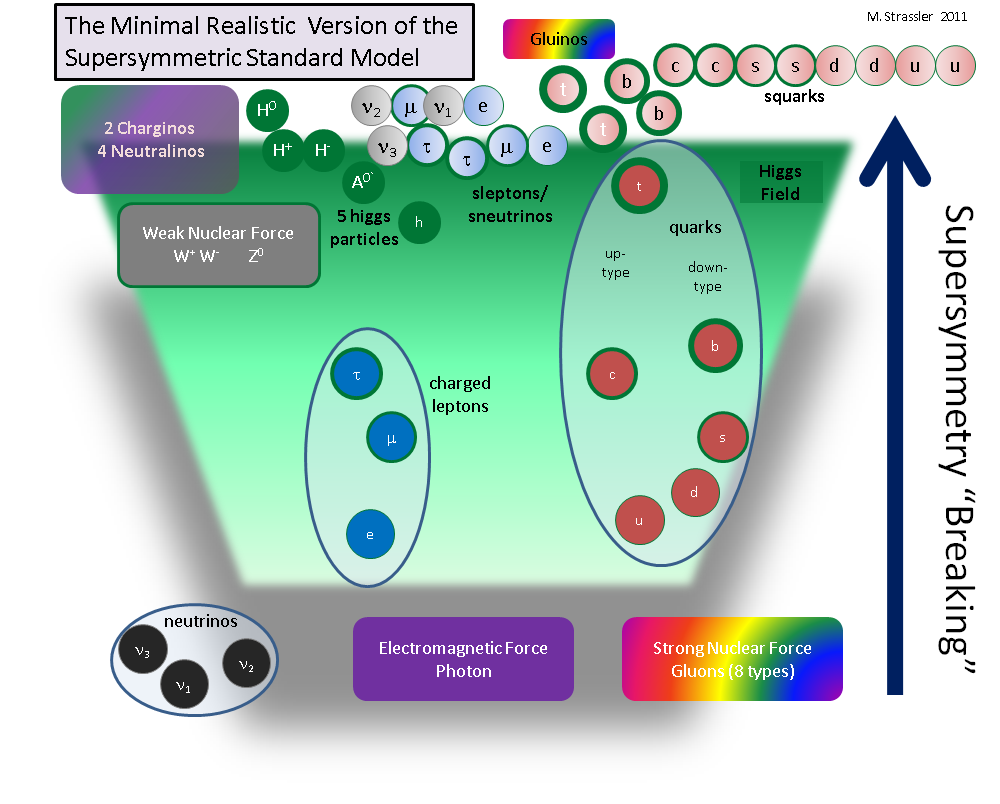
Рис. 3
Реалистичный возможный мир такого типа – возможно, похожий на наш – показан на рис. 3. Вы видите, что нарушение суперсимметрии (то, что она прячется и её нелегко обнаружить) увеличило масштаб масс всех суперпартнёров так, что вся массовая шкала находится выше массы верхнего кварка. И это не так искусственно или глупо, как кажется – математика с готовностью принимает этот эффект. Существует множество точных примеров того, как это может произойти – но их слишком много для того, чтобы мы догадались, какой из них наиболее вероятен.
В этом вероятном мире, показанном мною для вас, я сделал несколько произвольных допущений, но они довольно часто встречаются в подробных примерах нарушения суперсимметрии, изучаемых физиками-теоретиками, и мною в том числе:
• Скварки и глюино получили большую массу.
• Слептоны и снейтрино получили большую массу, но, вероятно, чуть меньшую, чем скварки и глюино.
• Вино, зино, фотино и хиггино замешались в набор электрически заряженных частиц, чарджино, и электрически нейтральных частиц, нейтралино, некоторые из которых, вероятно, немногим более массивные, чем W и Z.
• Пять частиц Хиггса обладают широчайшим спектром масс, хотя по меньшей мере одна из них довольно лёгкая.
И это не единственная схема, способная возникнуть при нарушении суперсимметрии! Существует большое количество других возможностей, которые я буду называть вариантами суперсимметрии. Но представленный мною вариант – наиболее популярный среди теоретиков и экспериментаторов, особенно в Европе (в США он менее популярен, про другие места я не знаю). Этой популярности есть веские причины; оказывается, что существует несколько независимых способов получить схему, сходную с этой. Однако популярность всегда порождает предвзятость, а нам необходимо рассматривать все возможности, не делая предположений касательно этих аргументов.
Но если суперпартнёры очень массивные, не может ли получиться так, что мы не сможем произвести ни одного из них в ближайшие десятилетия или даже столетия? Не занимаемся ли мы подсчётом количества ангелов, способных уместиться на кончике иглы? Из всего вышеизложенного пока действительно следует, что такой риск существует. Однако есть и более тонкий аргумент в пользу наличия суперсимметрии, благодаря которому у многих физиков есть надежда на то, что все эти суперпартнёры находятся в пределах досягаемости Большого адронного коллайдера. Это следует из того факта, что суперсимметрия решила бы проблему иерархии – одну из величайших загадок нашего мира.
Важным свойством природы, ставящим в тупик учёных, а в их числе и меня, является свойство иерархии – огромной разницы между свойствами слабого ядерного взаимодействия и гравитации. Эту иерархию можно описать несколькими разными способами, каждый из которых упирает на одно из её свойств. Например:
Масса мельчайшей возможной чёрной дыры определяет то, что известно, как планковская масса. Более точный способ определения этой величины – комбинация ньютоновской гравитационной константы G, квантовой [редуцированной] константы Планка ħ и скорости света с: планковская масса равна
Массы частиц W и Z, переносящих слабое ядерное взаимодействие, примерно в 10 000 000 000 000 000 раз меньше планковской массы. В связи с этим существует огромная иерархия масштабов массы между слабым ядерным взаимодействием и гравитацией.
Сталкиваясь с таким огромным числом, как 10 000 000 000 000 000, десять квадриллионов, физики естественным образом задают вопрос: откуда оно взялось? И у него может быть довольно интересное объяснение.
Но пытаясь найти это объяснение в 1970-х, физики увидели существование серьёзной проблемы, даже парадокса, скрывающегося за этим числом. Эта проблема, известная сейчас, как проблема иерархии, связана с размером ненулевого поля Хиггса, которое в свою очередь определяет массу частиц W и Z.
Ненулевое поле Хиггса имеет размер примерно 250 ГэВ, это даёт массу частиц W и Z равную примерно 100 ГэВ. Но оказывается, что из квантовой механики следует, что такой размер поля Хиггса нестабилен, это нечто вроде (аналогия неполная!) вазы, балансирующей на краю стола. Из известной нам физики, из квантового дрожания, вроде бы следует, что для поля Хиггса должно существовать два естественных значения – по аналогии с двумя естественными местами для вазы, либо твёрдо стоящей на столе, либо валяющейся разбитой на полу. И получается, что поле Хиггса вроде бы должно быть либо нулевым, или оно должно быть сопоставимым по размеру с планковской энергией, в 10 000 000 000 000 000 больше наблюдаемого значения. Почему же его значение получается ненулевым и таким крохотным, таким, на первый взгляд, неестественным?
Это и есть проблема иерархии.
Многие физики-теоретики посвящали заметную часть своей карьеры попыткам решения этой проблемы. Некоторые утверждали, что нам нужны новые частицы и новые взаимодействия (их идеи проходят под именами суперсимметрии, техницвета, малого Хиггса, и т.п.) Некоторые говорили, что наше понимание гравитации ошибочно, и что существуют новые, неизвестные измерения («дополнительные измерения») пространства, которые мы обнаружим в ближайшем будущем в экспериментах на БАК. Другие говорят, что тут и объяснять нечего, поскольку действует эффект отбора: Вселенная гораздо больше и разнообразнее, чем наблюдаемая нами часть, и мы живём в довольно неестественной части Вселенной в основном потому, что оставшаяся её часть непригодна для жизни – точно так же, как, несмотря на то, что каменистые планеты встречаются редко, мы живём на одной из них оттого, что только тут мы могли эволюционировать и выжить. Возможно, у этой проблемы существуют и другие, пока не придуманные решения.
Многие из этих из этих решений – уж точно все решения с новыми частицами и взаимодействиями, и с новыми измерениями – предсказывают, что новые явления можно будет увидеть на БАК. И постепенно, но неумолимо БАК исключает эти возможности одну за другой. Пока что мы не видели никаких неожиданных явлений. Но мы находимся только в начале пути.
Кстати, часто можно прочесть, как проблему иерархии связывают с массой частицы Хиггса. Это не так. Проблема с тем, что величина ненулевого поля Хиггса слишком большая. Строже говоря, квантовая механика подправляет не массу Хиггса, а квадрат массы Хиггса, изменяя потенциальную энергию поля Хиггса, а следовательно, и величину поля, и делает его нулевым или слишком большим. А это катастрофа, поскольку массы W и Z известны. Масса Хиггса неизвестна, поэтому она могла бы быть очень большой – если массы W и Z тоже были бы большими. Так что проблема заключается в массах W и Z – и в величине ненулевого поля Хиггса, проблема как с логической, так и с научной точки зрения.
Источник



