Помните добрый мультик про Панду Кунг Фу и «случайности, которые не случайны», как говаривал учитель-черепаха? Похоже он намекал на детерминизм.

В разговорной речи часто встречается понятие «случайность». Говоря более «сухим» языком — это случайное событие. Не столь важно, как правильно называть такое явление. Смысл простой — случайность с физической точки зрения подразумевает событие, которое может произойти, а может и не случиться. И всю философию тут полезно исключить.
Тогда появляется интересный вопрос. Где-то глубоко в теории, любая случайность по всей логике должна быть всё-таки детерминирована. То есть исчерпывающий набор факторов и детальное описание любого процесса должны дать возможность прогнозировать явление с высокой точностью.
Упрощу формулировку: Существование случайности описывается математически. Это событие с низкой вероятностью его существования. Дальше исходим из того, что математический аппарат настолько громоздкий, а явление настолько сложное, что мы, как это говорится «забиваем» и называем всё случайным. Хотя это просто событие с низкой, точно вычисляемой, вероятностью существования.
Отмечу, что лично моё мнение по вопросу всегда строилось на том, что любая случайность — это плохо просчитанная вероятность, где не хватает данных. Что случайность невозможна технически. Но тут на своём канале я обсуждал с уважаемым комментатором принцип работы процесса измерений в квантовом компьютере.
Квантовый компьютер использует логику эффекта наблюдателя. Относительно эффекта наблюдателя у меня тоже было чёткое мнение. Я исходил из того, что существует просто невероятное количество вариантов, которые можно подсчитать согласно методу определения вероятности. Это будет, скажем, 100 (не важно сколько точно, наверное больше), возможных сценариев. Мы «наблюдая» выберем «выпавший» как в лото.
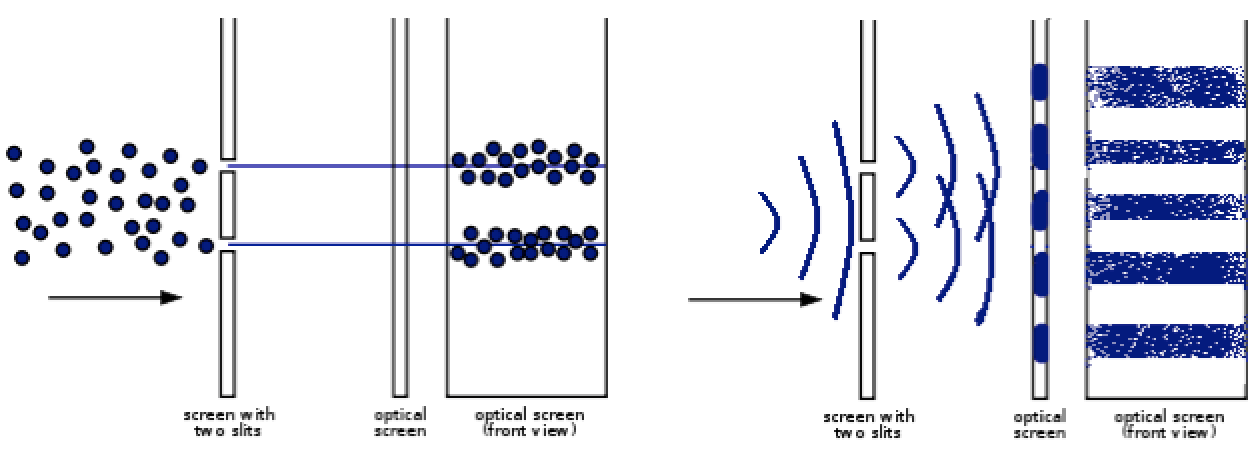
Вот только мой собеседник обвинил меня в использовании логики использования идеи «скрытых параметров». И на тот момент, я не мог представить, что случайность не детерминирована. Но такое мнение встречается мне всё чаще. Давайте попробуем ковырнуть глубже.
Случайности и точные науки
Точные науки они на то и «точные». Но возьмем, скажем, математику. Случайность, это такое событие, которое могло бы быть другим, но стало таким.
Теория вероятности делит события на три типа:
-
Невозможные — при данных условиях невозможны
-
Случайные — могут быть, а могут не быть
-
Достоверные — точно произойдут
Случайное событие происходит с некоторой вероятностью. События сравнивают по величине их вероятности. Например, в идеальном случае для монеты вероятность выпадения орла равна вероятности выпадения решки. И эти вероятности почти равны 0,5. Правда тут я бы «доковырялся» к этому классическому примеру и сказал, что с одной стороны монетка тяжелее, чем с другой. Значит, это точно не 0,5. Но это не суть беседы.
Как оказалось, я в своих размышлениях всегда опирался на так называемую теорию детерминизма. Она подразумевает, что если бы мы смогли запрограммировать все факторы и имели бы точное расчётное уравнение, то вычислить вероятность того или иного исхода при якобы «случайностях» не составило бы никакого труда. Причём, точность была бы 100%.
Эту логику «кроют» эффектом бабочки.
Дело в том, что большинство дифференциальных уравнений, описывающих реальные процессы, являются нелинейными уравнениями с неустойчивыми решениями относительно начальных условий.
Это подразумевает, что вроде как «точные» формулировки уравнений меняются ещё и сами вместе с изменениями условий.
Математика тут, вроде как, точная. Однако, изобилие решений делают процесс непрогнозируемым. Скажем, этакая задача трёх тел. Правда её сегодня, вроде как, уже смогли детерминировать. Но давайте рассматривать задачу трёх тел с позиции Ньютона, у которого из вычислительных устройств были, разве что счёты (и тех, не было, если серьезно). Каждое новое движение меняет расчётное уравнение.

В науке такое явление получило название «эффект бабочки». Если бабочка махнула крылышками, то где-то прошёл ураган. Таков один из возможных вариантов. Математика «оправдывает» это тем, что решение уравнения процесса будет по экспоненте отклоняться от предыдущего решения.
Два решения с очень близкими начальными условиями очень быстро станут диаметрально противоположны.
Что же…Всё равно не убедили
И всё-таки. Хорошо, многие процессы описываются нелинейными уравнениями. Предсказать что-то в объективном понимании невозможно. Компьютеры банально не умеют работать с некоторыми числами высокой точности, где есть миллионные знаки после запятой, а всё это может сказаться при наложении факторов и сработает эффект бабочки. Пусть так.
Но любое нелинейное уравнение — это всё-таки математический инструмент. Невероятно сложно учитывать все факторы. Их невозможно подсчитать и пересчитать. Результаты отличаются взрывным образом. Но всё это точная математика.
Тут я вижу два разрешения проблемы:
-
Или математический аппарат в принципе не может работать с высокими точностями. Значит, сколько уравнений не составляй, где-то мы упрёмся в предел вычислений и предел точности, и числа типа 0,56565689 и 0,56565683 будут иметь сходное физическое значение
-
Или всё-таки всё упирается в невозможность это подсчитать, а это уже совсем другая история и вся «магия» случайности пропадает и превращается в детерминированные значения
Есть ещё один вариант, о котором не хотелось бы тут писать. Вероятно, я сам не понимаю всю глубину и сложность тем нелинейных уравнений и вижу это излишне упрощенно.
Теория говорит, что в нелинейных системах взаимодействия могут влиять сами на себя: когда воздушные потоки протекают по крыльям реактивного самолёта, поток воздуха изменяет молекулярные взаимодействия, которые, в свою очередь, изменяют воздушный поток, и так далее.
Такая петля обратной связи порождает хаос, где небольшие изменения в начальных условиях позже приводят к крайне изменчивому поведению, что делает прогнозы практически невозможными.
Вот только отругайте меня в комментариях, если так нужно. Но это не исключает точный расчёт. Пускай условия хоть трижды влияют сами на себя. Они делают это согласно закономерности. Сложно не означает «невозможно». Всё упирается в ограниченность самой математики. Но это не отменяет детерминированности случайности.
В одной из статей было отмечено, что:
Эндрю Чайлдс из Университета Мэриленда возглавил работу, в которой учёные пытаются позволить квантовым компьютерам точнее моделировать нелинейную динамику. Алгоритм его команды превратил хаотичные системы в массив более понятных линейных уравнений с помощью метода линеаризации Карлемана. Джон Т. Консоли / Университет Мэриленда
Значит, если упрощение достигнуто, то и логика видимо работает. Правда здесь же отмечено, что квантовый компьютер технически не справится со всей проблемой. Ведь это устройство, которое тоже построено на линейной логической модели и заставить его решать такие вопросы — это как заставить машину летать.
Я так понимаю, что основная и главная проблема — невозможность применить линейность для работы с нелинейностью. Вся логика принципиально другая и дело тут не в философском понимании действительности. И тут я был бы благодарен за хорошие комментарии по теме. Ведь похоже нелинейность — это не просто закономерность по экспоненте или параболе, а что-то более глубокое. По крайней мере только это может оправдать существование случайности именно в том виде, как её преподносят в статьях про эффект наблюдателя.
П.с.: Подобные вопросы я часто разбираю на своём Telegram‑канале и буду рад гостям.

