Приветствую Вас! Сегодня хочу рассказать о геометрическом объекте, который похож на бумажный фонарик, но на самом деле является очень интересным контрпримером в области нахождения площади многогранников. Итак, поехали!
Парадокс лестницы
Архимед приближенно определял длину окружности с помощью длин сторон вписанных и описанных правильных многоугольников. В общем смысле, длину любой кривой можно выразить как наибольшее значение длин вписанных ломаных. Однако для корректной работы этого метода вершины ломаных должны находиться на самой кривой, а не просто рядом с ней.

В противоположном случае, как показано в так называемом «парадоксе лестницы», ломаные состоящие из вертикальных и горизонтальных отрезков общей длиной 2, могут быть расположены настолько близко к диагональному отрезку длиной √2, что они будут «визуально» сходиться к диагонали, но будут иметь разную длину.
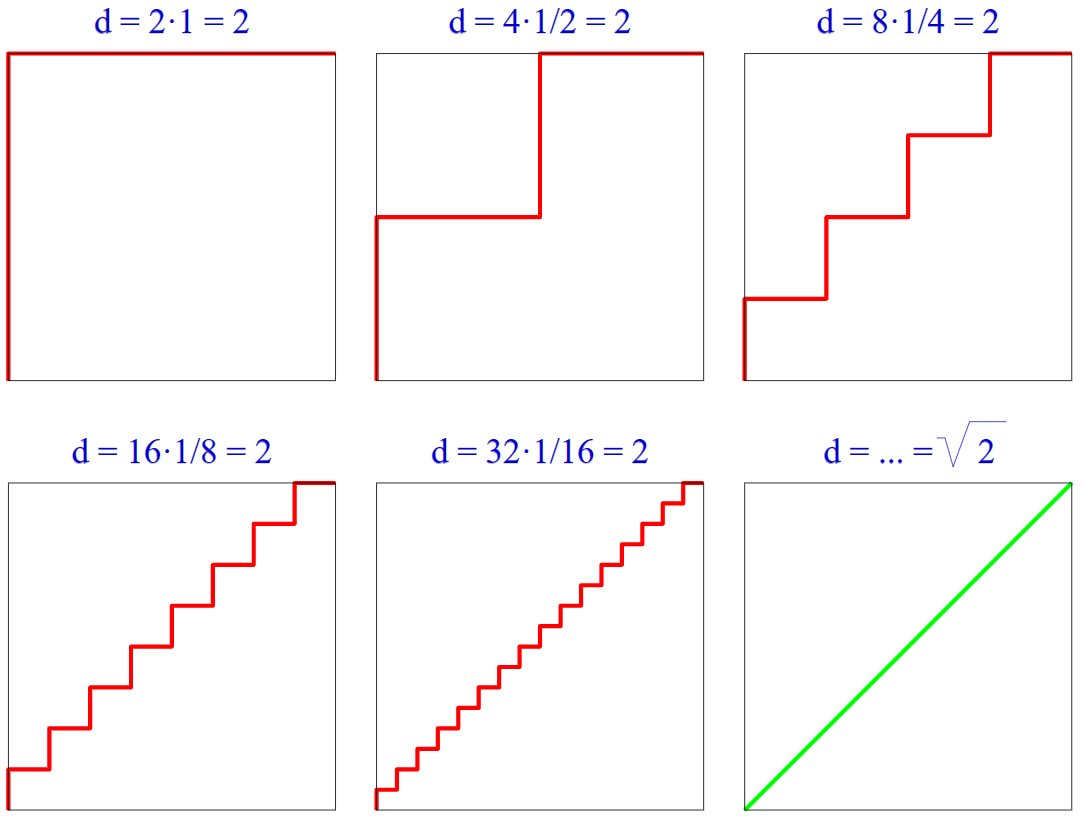
Сапог Шварца приводит аналогичный контрпример для площади поверхности, демонстрируя, что для точного приближения площади требуется еще больше, чем просто условие, что вершины лежат на искомой поверхности.

В конце XIX века немецкий математик Герман Шварц (1843-1921) разработал свою собственную конструкцию, которая послужила контрпримером к ошибочному определению, представленному в книге 1868 года Ж. А. Серре «Курс дифференциального исчисления и интеграла». В этой книге утверждалось, что.
Пусть часть криволинейной поверхности ограничена контуром C; мы определим площадь этой поверхности как предел, к которому S стремится площадь вписанной многогранной поверхности, образованной из треугольных граней и ограниченной многоугольным контуром Γ пределом которого является контур C. Необходимо показать, что предел S существует и что он не зависит от закона, согласно которому грани вписанной многогранной поверхности сжимаются.
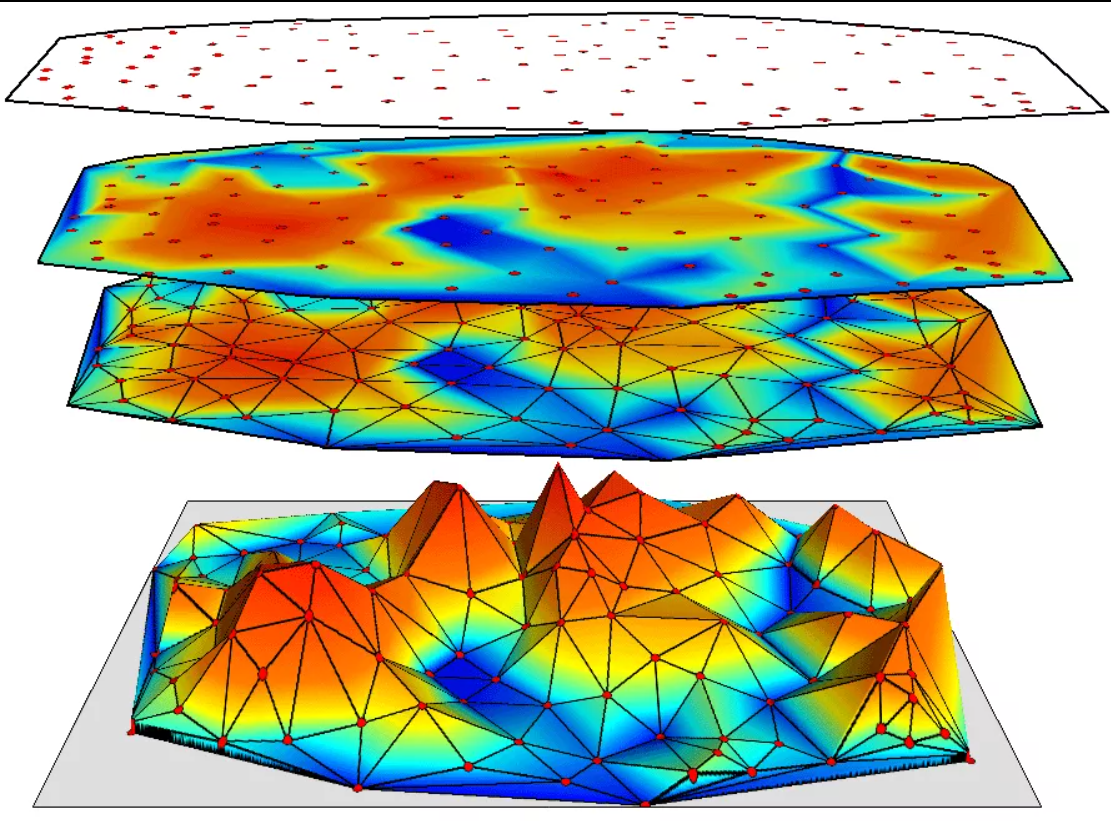
Конструкция сапога Шварца
Шварц разработал метод приближения поверхностей с помощью антипризм. Первый параметр антипризмы, обозначим его как «m», представляет собой количество кругов, второй параметр, обозначим его как «n», представляет половину числа треугольников в каждом кольце этой структуры. Для случая с одним кольцом (m=1) результирующая поверхность формируется из треугольных граней, составляющих антипризму порядка n.
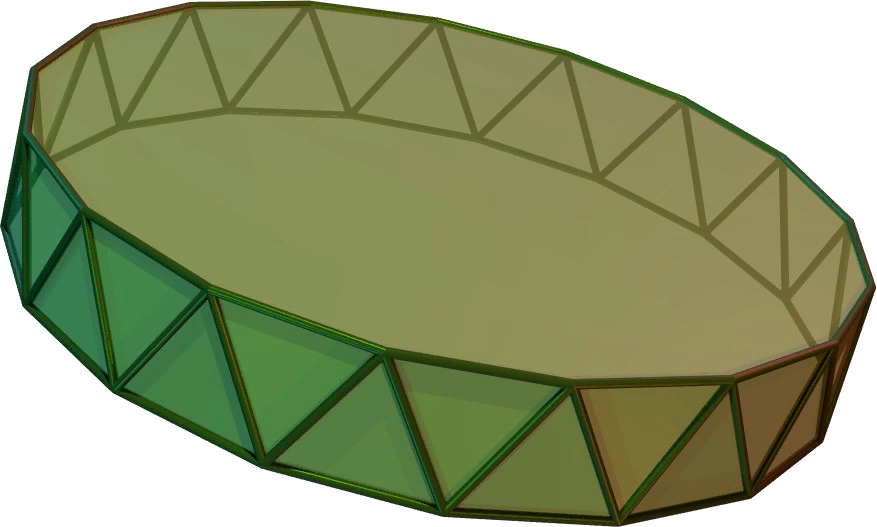
При более высоких значениях m, сапог Шварца формируется путем компоновки m таких антипризм.

Для построения сапога Шварца, который приближает заданный правильный круговой цилиндр, цилиндр разрезается на m блинов. Эти блины имеют m+1 круглых границ — две на концах цилиндра и еще одну на месте разреза. В каждом блине распределены n вершин, образуя правильный n-угольник (понятно, что количество этих углов можно увеличивать, стремясь ко сходству с окружностью).

Эти многоугольники повернуты на угол π/n от одной окружности к следующей, так что ребра правильных многоугольников и ближайшие вершины на следующем блине образуют основание и вершину равнобедренного треугольника. Эти треугольники пересекаются от края до края, образуя многогранную поверхность сапога Шварца, которая топологически эквивалентна цилиндру.

Сапог Шварца можно склеить из плоского листа бумаги с нанесенными на него гранями треугольников. Такой рисунок складок называется рисунком Йошимуры.

Если вывести формулу площади поверхности сапога Шварца, то получится следующее выражение.
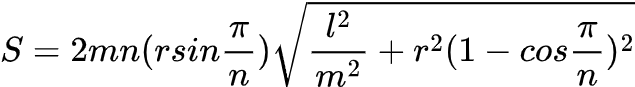
Парадокс
Если вычислить последовательно пределы, очевидно получится отличное приближение к площади поверхности цилиндра.
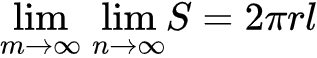
В этом случае внутренний предел уже сходится к нужному значению, а внешний предел является избыточным (иначе говоря, не важно, на сколько блинов будет разрезан цилиндр, вся апроксимация произойдет за счет большого числа треугольников).

В данном случае, при заданном значении n, с увеличением m и уменьшением длины каждой цилиндрической полосы l/m, каждая из соответствующих полос из равнобедренных треугольников становится практически плоской. Площадь поверхности каждого блина стремится к конечному числу, а так как во втором пределе мы неограниченно увеличиваем количество блинов, то общая площадь поверхности стремится к бесконечности.
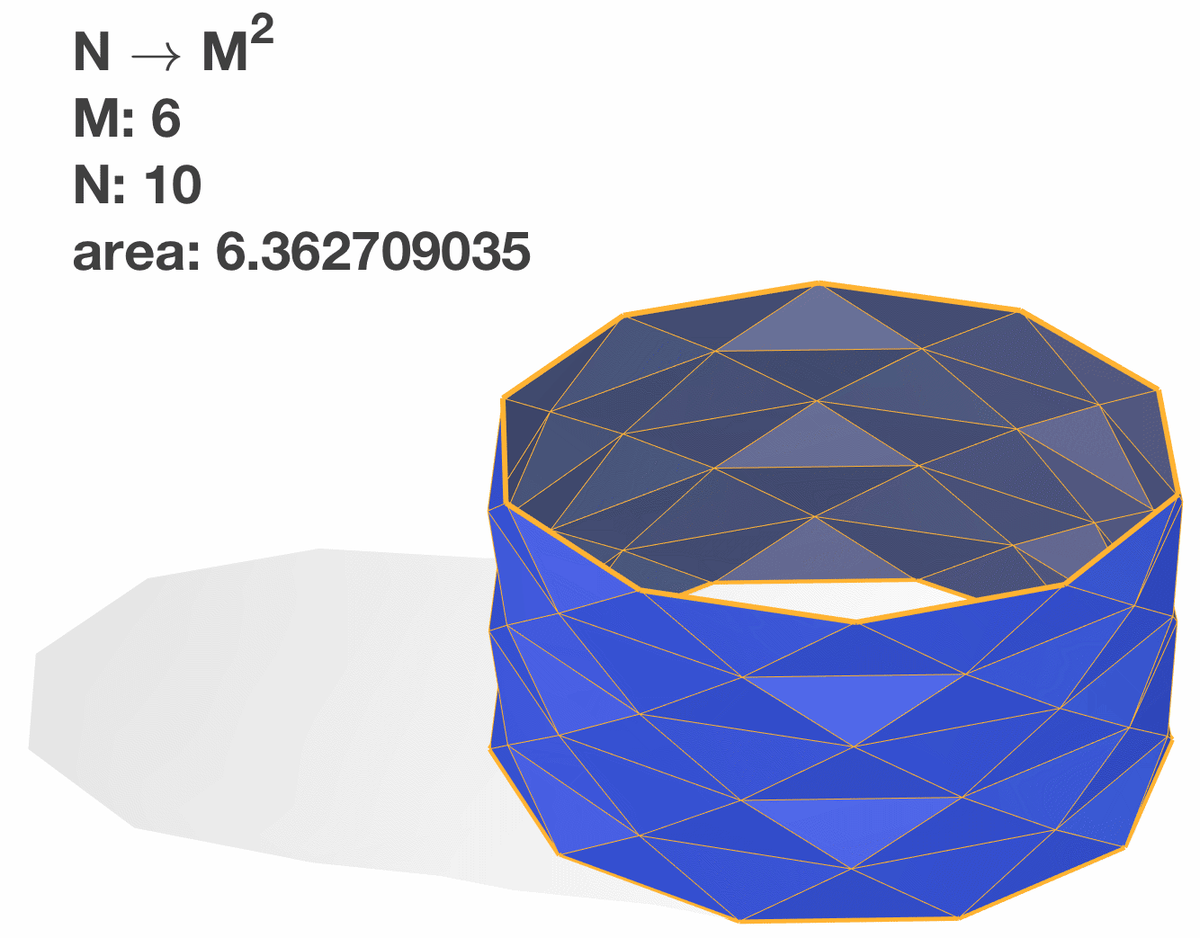
Также можно установить функциональную связь между параметрами «m» и «n» и исследовать предел при одновременном увеличении обоих параметров с сохранением этой связи.
Различные варианты такой связи могут привести к двум возможным сценариям: сходимости в определенной области или расходимости до бесконечности. Например, если выбрать m = cn (где c — произвольная константа) и рассматривать предел для больших значений n, то произойдет сходимость в определенной области. В то время как установка m = cn³ приведет к расходимости. Третий тип ограниченного поведения достигается при m = cn². Для данного выбора параметров, получим формулу.
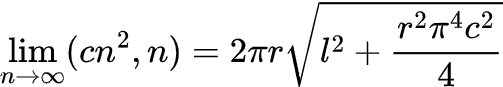
Играя значением c, можно получить любое значение площади поверхности. Показанное выше также подчеркивает важность тщательного выбора способа разбиения на треугольники для использования в компьютерной графике и методе конечных элементов, применяемом в научном и инженерном моделировании. В области компьютерной графики сцены часто представляются в виде треугольных поверхностей, и правильное отображение освещения зависит от ориентации нормалей к поверхности.
Все объемные выкладки — в одной статье.
Неправильный выбор способа разбиения на треугольники, подобно тому, как это происходит в случае с сапогом Шварца, может привести к образованию поверхности, наподобие складной гармошки, с нормалями, которые далеки от нормалей исходной поверхности. Близко расположенные резкие изгибы на этой поверхности также могут вызвать проблемы при сглаживании.
Проблемы возникают, когда в разбиение включены треугольники с углами, близкими к 180 градусам. В некоторых классах сапогов Шварца, которые используют углы ограниченные 180 градусами, площадь сходится к той же площади, что и у цилиндра, по мере увеличения числа треугольников до бесконечности.

Метод конечных элементов, в своей базовой форме, приближает гладкую функцию (часто представляющую решение задачи физического моделирования в науке или инженерии) путем замены её кусочно-линейной функцией на триангуляции. Пример с сапогом Шварца демонстрирует, что даже для простых функций, таких как высота цилиндра над плоскостью, проходящей через его ось, и даже если значения функции точно известны в вершинах триангуляции, использование триангуляции с углами, близкими к 180 градусам, может привести к значительно неточным результатам моделирования.
-
Больше математики в Telegram — «Математика не для всех«.


