И остались довольны результатом. Теперь хотят отправить ее на орбиту Земли.
Сегодня мы попробуем разобраться в физике пятого состояния материи и выясним, зачем ее сбрасывать с башни.
Бросание игрушек на пол – одно из самых ранних переживаний детства и источник бесконечной радости. Современная физика, какой мы ее знаем сегодня, также основана на последовательном стремлении к этому наивному удивлению по поводу гравитационного притяжения между материальными телами. Вклад Галилея, Ньютона и Эйнштейна в понимание свободного падения определил очертания современной физики.
Общая теория относительности основана на принципе эквивалентности, который гласит, что при свободном падении все объекты падают с одинаковой скоростью, независимо от их массы, при условии, что единственной действующей силой является гравитация. Это было доказано для больших объектов: легенда гласит, что Галилей сделал это первым, сбросив различные шары с Пизанской башни. Остается неясным, справедлива ли эквивалентность в квантовых масштабах, где эффекты гравитации недостаточно изучены. Выяснение этого может помочь создать квантовую теорию гравитации, одну из самых желанных целей современной физики.
Создать квантовый эквивалент теста Галилея непросто. В 2010 году команда под руководством Эрнста Раселя из Ганноверского университета в Германии наблюдала за квантовым объектом в свободном падении, сбросив конденсат Бозе-Эйнштейна вниз со 146-метровой башни. Конденсат Бозе Эйнштейна – облако охлажденных атомов, которое ведет себя как единый квантовый объект. Попробуем разобраться в физике этого странного состояния материи и выясним, зачем ее сбрасывать с башни.
▍ Немного истории
Как иногда хочется бросить все и отправиться в двадцатые годы двадцатого века. Но не для того, чтобы нарушить пространственно-временной континуум рукопожатием с Гитлером или Эйнштейном. Всегда не хватало возможности проникнуться атмосферой научной революции: растоптанными надеждами сохранить классические модели атома, отчаянием перед парадоксами релятивизма, отвращением к зарождающейся квантовой механике.
В ноябре 1924 года Луи де Бройль на защите докторской диссертации изложил идеи о волновых свойствах частиц. Комиссия мыслью не прониклась, а вот научный руководитель, Поль Ланжевен, не позволил работе кануть в небытие: сообщил о ней на Сольвеевском конгрессе и настоял на отправке копии Альберту Эйнштейну. Последний был восхищен и использовал наработки в зарождающейся квантовой статистике. В свою очередь, на идеи де Бройля опирался Эрвин Шредингер, когда выводил свое волновое уравнение в 1926 году.
И подумать только, в декабре того же 1924 года была опубликована статья Шатьендраната Бозе, которая заложила основы статистики Бозе-Эйнштейна. Также, в честь индийского ученого все частицы с целочисленным спином были названы бозонами. В чём разница между фермионами и бозонами на хабре уже обсуждалось. Далее Эйнштейн предсказывает существование того, что мы сегодня называем конденсатом Бозе-Эйнштейна. Однако теория была подвергнута критике Джорджем Уленбеком. Критика была в основном принята, так что Эйнштейн и другие физики некоторое время воздерживались от дальнейшего обсуждения этого состояния материи.
С 1935 года Фриц Лондон разрабатывает идею «макроскопической волновой функции» для теории сверхпроводимости, а в 37-м он услышал про статью о таинственном конденсате. На волне интереса к сверхтекучести и сверхпроводимости «пятое состояние вещества» тоже удостоилось внимания, так как во всех этих явлениях прослеживалась четкая аналогия. И затем в 50-х и 60-х многие важные теоретики атаковали проблему взаимодействия бозе-конденсированного газа. Это чертовски увлекательно: теория была далеко впереди экспериментов в этой области физики. Вплоть до 1995 года. Именно тогда стало возможно достижение вырожденного состояния для атомов щелочных металлов с помощью лазерного охлаждения. И в 2001 году достигших этого рубежа поощрили Нобелевской премией.
▍ Немного теории
Так вот, Билли, когда влажность соприкасается с холодной поверхностью стекла образуются холодные капельки, которые мы называем конденсатом…
Полицейский отряд, 1982
В квантовой статистике частицы классифицируются на две группы: фермионы с полуцелым значением спина и бозоны с целочисленным спином. В любой квантовой системе два фермиона не могут занимать одно и то же квантовое состояние, а у бозонов таких ограничений нет. Это было в статье «в чём разница между фермионами и бозонами«, так что не будем повторяться. К слову, и про принцип Паули был весьма интересный материал: «Что запрещает принцип Паули?«, так что нам уже более-менее привычен мир, в котором поворот на 360 градусов не возвращает в исходную позицию (не тождественное преобразование). Забавный пример проявления принципа запрета: чудовищная гравитация перерождающейся звезды может компенсироваться тем, что какие-то там фермиончики не хотят находиться в одном состоянии. (Не смогу удержаться от настойчивой рекомендации пройти бесплатный курс по астрофизике на Лекториуме).
Бозоны обделены таким отличительным признаком как полуцелый спин. И волновая функция двух бозонов симметрична относительно их перестановок, ведь они идентичны. Это как если бы вам сказали, что при броске двух монет, вероятность выпадения «орел + решка» равна 1/3. Совсем другая статистика. Бозоны обходят принцип запрета и при должных условиях могут все вместе занять одно состояние. Где взять бозоны? В первую очередь это частицы связанные с полем, из которых наиболее важным примером является фотон. Эти частицы не сохраняются: при изменении полной энергии поля частицы появляются и исчезают. Во вторых, это составные частицы, содержащие четное число фермионов. Число частиц сохраняется, если энергия не превышает энергию диссоциации (~ МэВ в случае ядра). То есть, достаточно, чтобы взаимодействия между композитами имели гораздо более низкую энергию, чем внутренние энергетические уровни. Также к бозонам можно отнести различные квазичастицы, но лучше пока на них не отвлекаться.
Термин «конденсация» происходит от латинского глагола «condensare», что означает прижиматься, уплотняться. Особенность конденсации Бозе-Эйнштейна заключается в том, что частицы не сближаются друг с другом в реальном пространстве, но они делают это в импульсном пространстве: многие частицы имеют тенденцию конденсироваться в состояние с наименьшим импульсом (соответствующему нулевой скорости), оставаясь при этом делокализованными в пространстве.
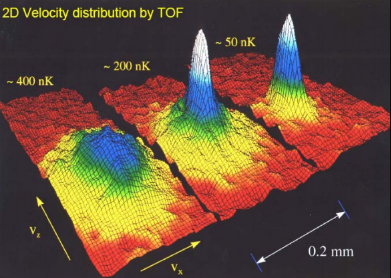
Когда эту иллюстрацию используют в популярных статьях, частенько выбирают минималистичный вариант без стрелочек и подписей, так что информативность теряется. В детстве я так себе и представлял пятое состояние материи – на поверхности флуктуирующей жидкости вырастает холмик сверхтекучего вещества. На самом же деле, это будет маленькая капля парящая в магнитной ловушке, а конденсация происходит именно по скоростям частиц, которые начинают теснится в основном состоянии с минимальной энергией.
Как помнится, в квантовой механике каждая частица с импульсом p имеет длину волны де Бройля λ = h/p, где h – постоянная Планка. Мы можем думать о λ как о типичном размере волнового пакета, связанного с частицей. Если мы рассмотрим процессы, связанные с масштабами, намного превышающими λ, то мы можем смело использовать классическую механику. И наоборот, на расстояниях порядка λ (или меньше) доминирует квантовая механика.
Вспомним классическую физику: наполним контейнер неидеальным газом и начнем снижать температуру. Плотность газа остается постоянной до тех пор, пока не произойдет конденсация. Поскольку плотность жидкости намного выше, чем у газа, то в дальнейшем плотность газа уменьшается с температурой. То есть, при понижении температуры, молекулы газа уменьшают свою среднюю скорость и начинают сближаться друг с другом, поскольку между ними начинает доминировать притяжение. Происходит фазовый переход из газовой фазы низкой плотности в жидкую фазу более высокой плотности.
При определенных плотностях длины волн де Бройля частиц становятся сопоставимы с расстояниями между ними. Еще одной важной величиной будет характерный масштаб взаимодействия между частицами – расстояние, на котором два бозона начинают ощущать притягательное взаимодействие между друг другом. В эксперименте обычно систему охлаждают, одновременно удаляя некоторые бозоны, так что их среднее расстояние остается достаточно большим, а взаимодействие между ними незначительно. Метод называется испарительным охлаждением: бозоны с высокими энергиями избирательно удаляются, так что система остывает до нанокельвинов, а плотность поддерживается низкой.
При экстремальном охлаждении бозонов, их длины волны де Бройля становятся больше, и поэтому неопределенность их положения возрастает. И они начинают занимать одно и то же квантовое состояние – основное состояние. Таким образом, у нас получается большое количество бозонов в одном и том же квантовом состоянии. Они неразличимы и делокализованы. Это означает, что мы можем описать систему этих частиц одной макроскопической волновой функцией.
▍ Немного квантмеха
Окей, у нас есть одна волновая функция, и она описывает состояние кучи частиц. Нам нужна формула, которая бы отображала динамику бозе-конденсата. Эволюция квантовой системы подчиняется уравнению Шредингера:
Странно, почему адекватные люди не используют шрёдингериан… Конечно, мы могли бы пойти по строгому пути, поднять вторичное квантование и начать играть с уравнением Гейзенберга, но чтоб статья не ушла в рейтинг 18+, будем применять мягкую и интуитивную последовательность преобразований. Для начала, рассмотрим содержимое только что введенного супероператора, опуская для простоты значки вектора:
Гамильтониан многих частиц. Если представлять их себе как стукающиеся шарики, то у нас записано выражение для суммарной энергии системы: кинетических энергий каждого шарика и потенциальных взаимодействий. У шариков есть импульсы и они чувствуют внешнее (external) поле, а также, влияют каждый на друг друга. Взрослые же люди здесь видят лишь операторы действующие на вектор состояния в гильбертовом пространстве.
Зависящее от времени уравнение Шредингера для многих тел является уравнением Эйлера-Лагранжа следующего функционала действия:
Второе тождество заключает в себе суть вариационного принципа Дирака-Френкеля, характеризующегося стационарностью квантового эффективного действия. Вариационный принцип в физике – это альтернативный метод определения состояния или динамики физической системы путем идентификации ее как экстремума (минимума, максимума или седловой точки) функции или функционала.
В случае чистого конденсата Бозе-Эйнштейна предполагается, что все бозоны находятся на одной и той же зависящей от времени одночастичной орбитали (анзац Хартри)
Для пущей понятности приведены две формы записи: волновые функции и кеты с тензорными произведениями. Данное приближение подразумевает, что частицы независимы и взаимодействуют только через кулоновский потенциал среднего поля. В конце концов у нас будет нелинейная динамика с малыми, но ненулевыми взаимодействиями и энергиями возбуждения.
Теперь начинаем аккуратненько перебирать слагаемые из шрёдингериана:
Здесь мы вспомнили как находить производную произведения. Судьба редко предоставляет случай воспользоваться таким навыком, так что наслаждаемся.
Бозоны независимы и это упрощает задачу: для кинетической энергии и внешнего потенциала получается набор интегралов по объему – по одному на каждую частицу, и каждый записан в наимилейшей «бра-кет»-нотации. А для метаморфозов треугольничков используются тождества Грина. Даже если непонятно что происходит, следует хотя бы насладиться красотой формул.
Ранее указывалось, что мы работаем с разреженными газами – типичное межатомное расстояние намного больше, чем диапазон потенциального взаимодействия. Как следствие, взаимодействия могут с высокой степенью точности рассматриваться как события рассеяния двух тел. И для разреженного газа бозонов тогда можно использовать псевдо-потенциал Ферми:
Длина рассеяния измеряет интенсивность взаимодействий между бозонами, а дельта-функция показывает, что взаимодействие частиц включается при «столкновении». Так-то в реальном мире взаимодействия могут действовать далеко, корреляции нет-нет да сохраняются на больших пространственных и временных масштабах, и частенько кажется, что для постижения естества нужно учитывать связь всего со всем. Но почти всегда эти связи имеют пренебрежимо малые порядки малости и тонут в фоновых шумах, так что их можно смело отбрасывать, а астрологи и эзотерики идут лесом.
Ну вот, теперь у нас есть четыре слагаемых шрёдингериана заключенные в «ско» и «бки», и у каждого торчит константа N. Избавимся от нее перенормировкой и соберем все вместе:
Получился самый что ни на есть замечательный гроссапитаевскиан! И как известно, из гроссопитаевскиана совершенно непринужденно получается уравнение Гросса-Питаевского
Также его называют просто нелинейным уравнением Шрёдингера. Существует множество вариаций данного уравнения отличающихся характером нелинейности (дополнительные слагаемые высших степеней, логарифмическая нелинейность и т. д.). Самое интересное, что это уравнение находит применение во многих областях: физика плазмы, нелинейная оптика, квантовая химия, материаловедение, биология и сверхтекучие жидкости. Наиболее интересные применения мы еще рассмотрим в следующих статьях.
▍ Немного кодинга
Уравнение Гросса-Питаевского – это уравнение в частных производных. Самым наивным способом его решения будет применение конечных разностей. Есть также более специфичные методы типа схемы Дюфорта-Франкела или релаксации Бессе. Но на первый раз мы позволим себе готовый солвер и не будем заглядывать под капот, а уже в следующей статье разберем всю подноготную.
Для решения уравнения воспользуемся пакетом QuantumOptics.jl. Это вычислительная платформа с открытым исходным кодом, созданная для моделирования и исследования открытых квантовых систем. Пакет выполнен на языке Julia и призван быть интуитивно понятным в использовании с лучшей производительностью, чем у альтернатив, таких как Quantum Toolbox в Python или Quantum Optics Toolbox в Matlab. В QuantumOptics.jl существуют различные базисы, которые используются для формализации задачи. После определения базиса задаются квантовые объекты, такие как состояния и операторы, которые «знают», в каком базисе они определены. Невозможно по ошибке применить оператор к состоянию, которое не находится в том же базисе. Кроме того, есть возможность применять различные временные эволюции или другие операции к квантовым объектам. Следует отметить, что QuantumOptics.jl поставляется с исчерпывающей и очень полезной документацией со множеством примеров.
Разберем тривиальнейший случай моделирования частицы в гармонической ловушке:
В первую очередь необходимо задать базис. Для частиц есть два распространенных варианта. Мы можем работать в координатном (реальном) или импульсном пространстве.
using QuantumOptics, PyPlot
m = 1.
ω = 0.5
xmin = -5
xmax = 5
Npoints = 100
b_position = PositionBasis(xmin, xmax, Npoints)
p = momentum(b_position) # Dense operator
x = position(b_position) # Sparse operator
H = p^2/2m + 1/2*m*ω^2*dense(x^2)
Пространственный базис определяется диапазоном позиций от до
. Количество точек N в конечном счете определяет размерность базиса. Конечно, мы могли бы также поработать в импульсном пространстве:
b_momentum = MomentumBasis(b_position);
p = momentum(b_momentum) # Sparse operator
x = position(b_momentum) # Dense operator
H = dense(p^2)/2m + 1/2*m*ω^2*x^2Однако оба варианта не являются оптимальными, поскольку в реальном пространстве оператор координаты является диагональным, в то время как оператор импульса представляет собой плотную матрицу, и наоборот для пространства импульса. Следовательно, расчет будет масштабироваться как N², где N – размерность гильбертова пространства. Обычно используется трюк заключаемый в использовании быстрого преобразования Фурье для преобразования состояния системы между реальным и импульсным пространством. Это позволяет всегда использовать диагональную форму операторов, которая в целом ускоряет вычисления до N log N.
Эта идея реализуется оператором transform, который выполняет быстрое преобразование Фурье переводя состояние из координатного в импульсное пространство:
T_px = transform(b_momentum, b_position)
T_xp = dagger(T_px)
x = position(b_position)
p = momentum(b_momentum)
H_kin = LazyProduct(T_xp, p^2/2m, T_px)
V = ω*x^2
H = LazySum(H_kin, V)Чтобы использовать этот оператор в гамильтониане, нам дополнительно нужна концепция ленивых операторов, которые позволяют откладывать определенные операции на более поздний этап моделирования. Например, LazyProduct позволяет выполнять A*(B∗x) вместо (A∗B)∗x. Это означает для нашего случая, что произведение матрицы на матрицу не будет вычисляться напрямую, а вместо этого происходит только два умножения матрицы на вектор. То есть, происходит задержка вычислений до тех пор, пока оператор не будет применен к состоянию.
Наконец, мы можем смоделировать эволюцию системы подчиняющуюся уравнению Шредингера
x0 = 1.5
p0 = 0
sigma0 = 0.6
Ψ0 = gaussianstate(b_position, x0, p0, sigma0);
# эволюция во времени
T = [0:0.1:3;]
tout, Ψt = timeevolution.schroedinger(T, Ψ0, H);
# иллюстрация плотности вероятности
x_points = samplepoints(b_position)
n = abs.(Ψ0.data).^2
V = ω*x_points.^2
C = maximum(V)/maximum(n)
figure(figsize=(6,3))
xlabel(L"x")
ylabel(L"| Psi(t) |^2")
plot(x_points, (V.-3)./C, "k--")
for i=1:length(T)
Ψ = Ψt[i]
n .= abs.(Ψ.data).^2
plot(x_points, n, "C0", alpha=0.9*(float(i)/length(T))^8+0.1)
end
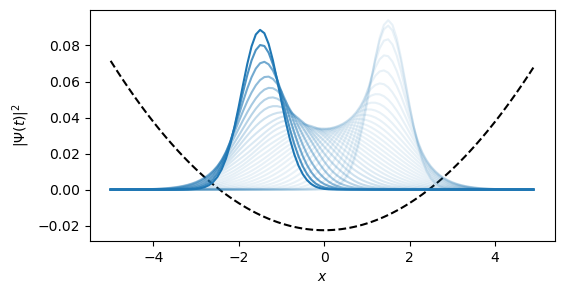
Уравнение Гросса-Питаевского будет отличаться лишь наличием нелинейности. Аналитическим решением данного уравнения является солитон, так что добавим возможность сравнения численного решения с аналитикой, завернем все в одну функцию и упростим нагрузку на средства построения графиков выбором из решения фиксированного количества точек.
using Plots, QuantumOptics
cd(s"C:UsersUserDesktopMycopplots")
soliton( x, t = 0, x₀=2., A₀=2.0, vx = -4.0 ) =
A₀*exp(im*(vx*x + (A₀^2-vx^2)*0.5*t)) * sech(A₀*(x-x₀-vx*t));
function nlse_qo( psi0, Vext, Nx, Nt; dt = 0.0005, α = 0.5, σ = 1.0,
scale = 128, xbox = (-10, 10) )
dx = (xbox[2]-xbox[1]) / Nx
T = range(0, step = dt, length = Nt)
tcut = Nt ÷ scale
xcut = Nx ÷ scale
xscaled = xcut:xcut:Nx
tscaled = tcut:tcut:Nt
bx = PositionBasis(xbox[1], xbox[2], Nx)
X = samplepoints(bx)
bp = MomentumBasis(bx)
Tpx = transform(bp, bx)
Txp = dagger(Tpx)
p = momentum(bp)
V = Vext( position(bx) )
Hkin = LazyProduct(Txp, α*p^2, Tpx)
Hψ = diagonaloperator( bx, Ket(bx).data ) #∝|ψ|²
Ho = LazySum(Hkin, Hψ, V )
function H(t, ψ)
Hψ.data.nzval .= -σ*abs2.(ψ.data)
return Ho
end
ψo = Ket(bx, psi0.(X))
tout, ψt = timeevolution.schroedinger_dynamic(T, ψo, H)
psi = [ ψ.data[j] for j = xscaled, ψ=ψt[tscaled] ]
psiex = [ psi0(x, j*dt) for x in X[xscaled], j in tscaled ]
return X[xscaled], T[tscaled], psi, psiex
end
@time X0, T0, psi0, psiex = nlse_qo(soliton, x-> 0.0*x, 256, 2^17,
dt = 2e-5, scale = 128, xbox = (-4π, 2π));
contour(T0, X0, real.(psi0), colorbar = true, fill = false)
p1 = xaxis!("t"); yaxis!("x")
plot(T0, [ sum(abs2.( psi0[:,i]-psiex[:,i] ) ) for i ∈ 1:length(T0) ],
lab = "error" )
p2 = xaxis!("t"); yaxis!("∑|ψᵢ-ψᵢᵉˣ|²") # exact
plot(p1, p2, layout = (1,2) )
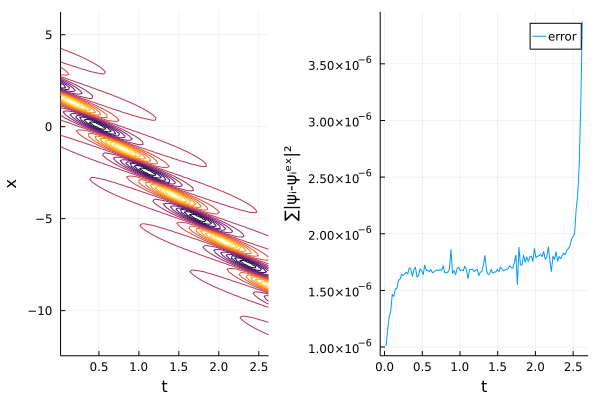
На левом изображении контур решения – путешествие солитона во времени. Первый пуск вычислений идет гораздо дольше: помимо главной джулийской боли time-for-first-plot еще приходится ждать разогрева ленивых операторов, зато потом считает как по маслу. Добавим-ка теперь гармонический потенциал:
@time X, T, psi5, psiex = nlse_qo(soliton, x-> 0.5*x^2, 256, 2^17,
dt = 4.9e-5, scale = 256, xbox = (-3π, 3π));
contour(T, X, real.(psi5), colorbar = true, fill = true)
xaxis!("t"); yaxis!("x")
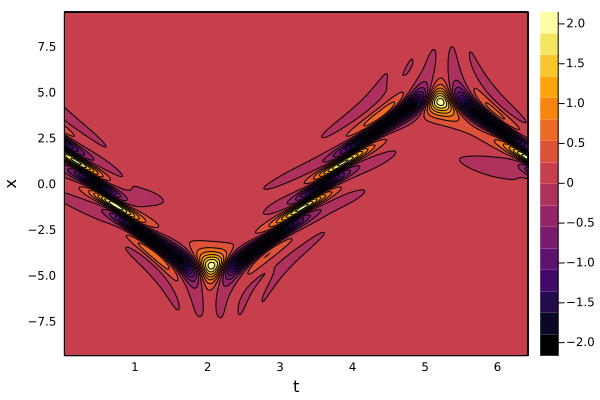
Солитон зажатый в ловушке! Но красивей будет в динамике
Y = 0.5*X.^2
Y /= maximum(Y)
anim = @animate for i ∈ 1:length(T)
psi_i = real.( psi5[:,i] )
psi_i /= maximum(abs.(psi_i))
psabs = abs2.( psi5[:,i] )
psabs /= maximum(psabs)
plot( X, psi_i, line = (2, :red), marker = (5, 0.8, :red) )
plot!(X, Y + psabs, line = (1, :gray), fill = (0, 0.4, :gray) )
plot!(X, Y, line = (3, :dash, :blue), legend = false )
yaxis!((-1, 2))
end
gif(anim, "1d_BEC.gif", fps = 10)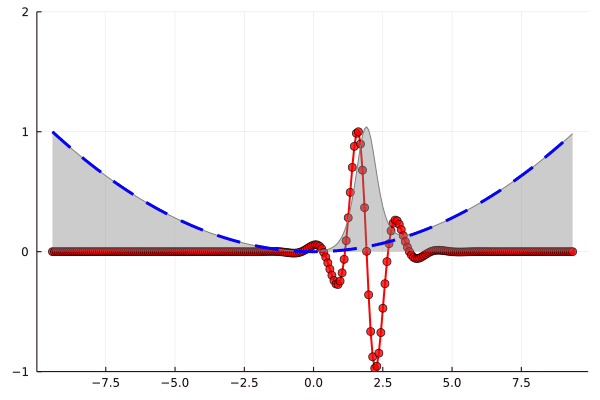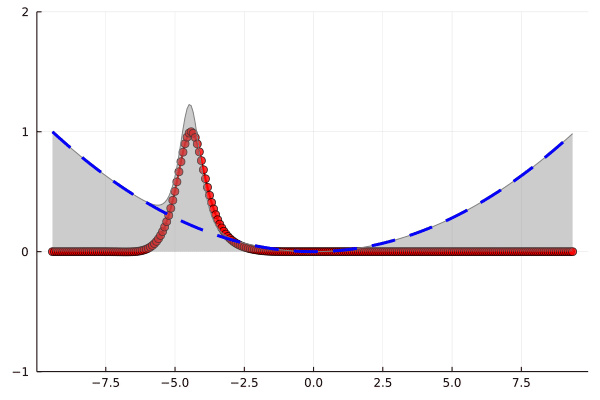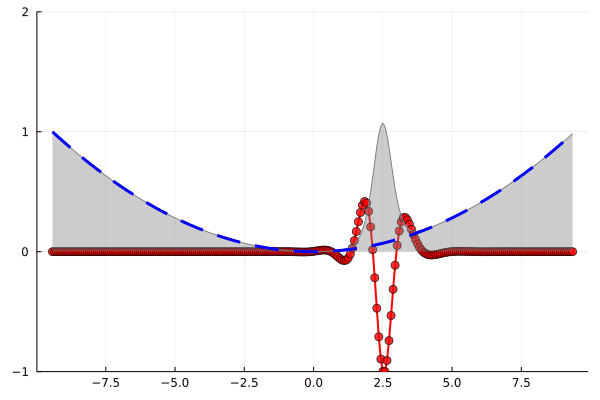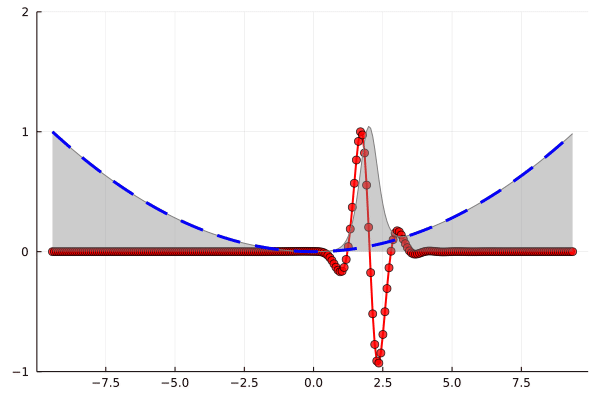
Синее — потенциал, красное — реальная часть комплекснозначного решения, серое — абсолютная часть, зеленое — материальное поощрение за мои старания
Хороший способ визуализации эмоциональных качелей посредством моделирования динамики солитона в конденсате Бозе-Эйнштейна! Теперь дело за малым – обобщить на двух- и трехмерный случай, задать соответствующие значения параметрам и вперед, моделировать капельки и пузырьки в магнитной ловушке. И что примечательно, результаты очень неплохо согласуются с экспериментами, например, вот череда снимков, где верхняя строка – реальный бозе-конденсат, а нижняя – численное решение уравнения Гросса-Питаевского:
Ширина каждой рамки 70 мкм. Так как получение изображения разрушительный процесс, то каждому снимку соответствует новый КБЭ
И теперь пришло время перейти к вопросу, который меня мучает с начальных классов: как делают бозе-конденсаты.
▍ Эксперименты
Итак, берем разреженный газ бозонов, для чего сойдет рубидий, литий, натрий, гелий, калий, хром или, скажем, иттербий (разумеется, подойдет не всякий изотоп). Мы помним, что частица поглотит фотон, если его частота чётенько соответствует разности между уровнями энергий для состояний, которые эта частица может занимать. Значит, для нашего разреженного газа нейтральных атомов применимо лазерное охлаждение: настраиваем частоту лазера чуть меньше этой разности энергий, и тогда атом рассеивает (поглощает и повторно излучает) фотоны только в том случае, если он движется в направлении лазера (эффект Доплера). Атом, находящийся в состоянии покоя или движущийся в противоположном направлении, не рассеивается. Если резонансный фотон поглощается, атом переизлучает фотон с большей частотой в произвольном направлении и при этом тормозится. Скорость движения падает и газ охлаждается.
Этого хватит, чтобы дойти до температур порядка микрокельвина. В такой ситуации скорость атома будет около нескольких см/с, а медленно движущиеся атомы относительно легко заключить в неоднородную магнитную ловушку. Магнитное поле имеет минимальное значение в центре «магнитной чаши». Атом со спином, параллельным магнитному полю (т. е. атомный магнитный момент полю антипараллелен), притягивается к минимуму; для спина, антипараллельного полю, атом отталкивается от минимума. Частицы стекаются в чашу, потихоньку копошатся, стукаются между собой и те, что поэнергичней, ловушку покидают, тем самым понижая энергию системы. Это аналогично испарению воды – процессу, из-за которого мы чувствуем прохладу выходя из душа.
А дальше можно догнаться радиочастотным принудительным испарительным охлаждением. Резонансное возбуждение переворачивает спины, и определенные атомы (с более высокой энергией) выбрасываются (испаряются). Но стоит помнить, что хотя взаимодействия слабы в полученной испарине, они достаточно сильны для фазового перехода пар-твердое тело при сверхнизких температурах. В условиях теплового равновесия сложно откачивать энергию без разделения фаз. И как сделать, чтобы весь газ вдруг не обратился в лед? Ключ к успеху – метастабильность. Если процесс охлаждения достаточно медленный и «мягкий», можно получить «сверхнасыщенный» пар без образования кристаллической фазы. Для этого необходимо исключить не только взаимодействие со стенками, но и столкновения трех частиц, которые способствуют образованию молекул и, в конечном счете, фазы конденсированного вещества высокой плотности.
И на последнем этапе, для наблюдения за распределением скоростей атомов в системе магнитная ловушка выключается. Атомы оказываются в свободном пространстве, и, поскольку у них есть некоторая остаточная скорость, они просто разлетаются по сторонами, а полученное облако фоткается лазером. Вот и весь эксперимент.
Ладушки, у нас есть облако сотен тысяч атомов композитных бозонов, которые были охлаждены до температуры нанокельвина с помощью лазеров и магнитных полей. При таких температурах все атомы ведут себя вместе как единый квантовый объект. Этот объект обладает такой низкой энергией, что его можно использовать для определения очень низких магнитных полей, свойство, которое используется для исследования новых материалов, таких как нанопроволоки серебра, наноматериалы из нитрида кремния или для исследования ионных каналов в биологических клетках. В общем, КБЭ отличный квантовый сенсор. И такой сенсор можно использовать для гравиметрии.
 В настоящее время гравитационное поле Земли находится под более пристальным вниманием, чем когда-либо прежде. С одной стороны, интересна сложная геодинамика классического гравитационного поля Земли. От приливных движений океанов и потоков атмосферных масс до мельчайших колебаний мгновенных осей вращения Земли из-за движения жидкого ядра, все такие эффекты становятся измеримыми. Это делается либо с помощью наземных гравитометров, которые измеряют зависящее от времени локальное ускорение, либо в космосе, где спутниковые геодезические измерения устанавливают более жесткие ограничения на более высокие мультипольные моменты гравитационного потенциала. Другое направление исследований больше фокусируется на фундаментальных аспектах гравитации, вытекающих из общей теории относительности. И тут эйнштейновский конденсат помогает проверить эйнштейновский принцип эквивалентности.
В настоящее время гравитационное поле Земли находится под более пристальным вниманием, чем когда-либо прежде. С одной стороны, интересна сложная геодинамика классического гравитационного поля Земли. От приливных движений океанов и потоков атмосферных масс до мельчайших колебаний мгновенных осей вращения Земли из-за движения жидкого ядра, все такие эффекты становятся измеримыми. Это делается либо с помощью наземных гравитометров, которые измеряют зависящее от времени локальное ускорение, либо в космосе, где спутниковые геодезические измерения устанавливают более жесткие ограничения на более высокие мультипольные моменты гравитационного потенциала. Другое направление исследований больше фокусируется на фундаментальных аспектах гравитации, вытекающих из общей теории относительности. И тут эйнштейновский конденсат помогает проверить эйнштейновский принцип эквивалентности.
Ранее отмечалось, что для удержания конденсата БЭ нужно магнитное поле, что применимо к однотипным атомам – поле настраивается под конкретное вещество, а хотелось бы проводить сравнительный анализ смесей. Еще конденсат чувствителен к гравитации, которая выбивает атомы из ловушки и препятствует эффективному охлаждению. Эта чувствительность как раз и позволяет использовать конденсат Бозе-Эйнштейна для сверхчувствительных инерционных акселерометров. Также гравитация уменьшает время наблюдения за облаком квантового газа: после освобождения из магнитной ловушки оно просто падает на стенку испытательной камеры. И в то же время, для изучения гравитации хотелось бы поместить свободно расширяющийся КБЭ в интерферометр, так как интерференционная картина будет частично зависеть от гравитационных эффектов, обусловленных массой атомов. В общем, у нас достаточно оснований, чтобы отправить бозе-газ вместе со всем измерительным оборудованием в свободное падение.
Схема эксперимента: капсула с оборудованием спускается по шахте с высоты 120 метров
В 2010 году, охладив газ из атомов рубидия до девяти миллиардных долей градуса выше абсолютного нуля, исследователи спустили экспериментальную капсулу со всем оборудованием и конденсатом по шахте внутри 146-метровой башни, построенной для исследования микрогравитации в Бременском университете в Германии. И так 180 раз по три капли в день. На дне шахты капсулу встречает 8 метров полистироловых шариков – а людей туда прыгать пускают? Короче идея состояла в том, чтобы заставить квантовый объект свободно расширяться во время падения, которое длится около 5 секунд. Но для наблюдения выходит окно в одну секунду, так как часть времени уходит на контроль остаточных колебаний и прочие издержки.
А уже в этом году удалось получить долгоживущий квантовый газ с температурой 38 пК – половина десятимиллиардной доли градуса выше абсолютного нуля! Использовалась новая техника 3D-коллимации: ловкое сочетание режима включения-выключения магнитной линзы с коллективным колебательным возбуждением конденсата позволяет увеличить время жизни осциллирующей капли и сохранение низкой температуры. Настраивая как время колебаний при выходе конденсата, так и силу потенциала магнитной линзы, этот новый метод дает возможность конструировать и контролировать форму облака квантового газа, что дает материал живущий несколько десятков секунд. Он пригодится для высокоточного обнаружения гравитационных волн, измерения гравитационной постоянной и приливной силы тяжести, а также для поиска сверхлегкой темной материи и строгой проверки принципа эквивалентности Эйнштейна.
Далее стоит обратить внимание на полноценную интерферометрию свободного бозе-конденсата, полет с 240 километров и эксперименты на МКС. А главным рубежом будет тестирование теорий квантовой гравитации, для чего пора накапливать эмпирические данные. И капелька сверхохлажденного квантового газа должна в этом помочь.
▍ Ссылкография
- Вывод УГП вторичным квантованием смотрим в Physics of Low-Dimensional Ultracold Bose Gases, Solitons in Bose-Einstein Condensates, The Gross-Pitaevskii Equation and Bose-Einstein condensates, и если запутают коммутаторы, то помощь есть на stackexchange, а теорию рассеяния смотрим в Chapter 3 The Gross-Pitaevskii equation.
- Quantum Bubbles in Microgravity, Generating Solitons by Phase Engineering of a Bose-Einstein Condensate — эксперименты с солитонами в КБЭ.
- Testing weakest force with coldest spot
- Mathematical Models & Numerical Simulation for Bose-Einstein Condensation
- Bachelor-Thesis 2D Solitons in QuantumOptics.jl
- Dropping cold quantum gases on Earth over long times and large distances 2008 — самая userfriendly статья, что я видел в жизни
- Bose-Einstein Condensation in Microgravity 2010
- Физики впервые получили бозе-конденсат в невесомости 2018
- Бозе-конденсат на МКС показал рекордное время свободного расширения 2020
- Quantum gravity could soon be tested using ultracold atoms 2021
- The Bose-Einstein Condensate and Cold Atom Laboratory 2021



