Рассмотрение вопроса скорости истечения воздуха под высоким давлением из малого отверстия в вакуум по материалам учебников для ВУЗовской специальности «Криогенная техника».
В комментариях к одной моей предыдущей статье «Дросселирование воздуха. Истечение воздушной струи из ресивера в атмосферу со сверхзвуковой скоростью» разгорелась бурная дискуссия с читателем @IGOR_KULIKOV.
Прочитать её можно по ссылке:
https://habr.com/ru/articles/768916/
Спасибо, Игорь, за ценные замечания!
В результате по рекомендации Игоря Куликова я нашёл учебник .
В.И. Иванов «ВАКУУМНАЯ ТЕХНИКА» 2016г, ГУ ИТМО
Привожу скрины страниц из этого учебника (см.рис.1-4)

Рис.1. Титульный лист учебника

Рис. 2. Лист с аннотацией учебника. ГУ ИТМО- это весьма уважаемое учебное заведение, как и инженерные специальности, для которых он предназначен.

Рис.3. Листы учебника с основными определениями применяемых значений при расчёте процессов Дросселирования воздуха в трубопроводах через малые отверстия.


Рис.4. Некоторые важные формулы из нескольких страниц учебника В.И. Иванов «ВАКУУМНАЯ ТЕХНИКА» 2016г ГУ ИТМО.
Что такого важного в этих страницах?
Важно то, что существует предел проводимости дросселирующего отверстия при перепаде давления более (Р1/Р2)кр, при этом расход Umax имеет совершенно однозначный предел (см. формулу (2.9) на скрине листа учебника.(см.рис. 4.)
При подстановке фиксированных константы для воздуха К=1,4 в это выражение при комнатной температуре Т=293К, и получаем значение Umax= 0,634*313=198,4м3/с на 1 м2.
Собственно важен сам коэффициент 0,634= (2/(к+1)^(1/(к-1)
То есть на скорости звука Vам=313м/с проходит только 63% массы газа от возможных по 100% сечения, при этом расход газа в отверстие считается с плотностью q1 при давлении Р1.
Кстати, скорость звука в учебнике по ЖРД имеет более простое значение, и для воздуха даёт отличающееся на 10 % значение:
Vaм=(к*R*T/М)^0,5=(1,4*8,31*293/0,029)^0,5=342м/с
Этот разнобой формул по одному вопросу уже наводит на мысль о местечковости формул в каждом отраслевом учебнике.
Но продолжим расчёт по учебнику «Вакуумная техника» для ИТМО.
Так как дросселированные – это процесс изменения плотности с разгоном по трубе без изменения температуры, то все пересчёты при «вакуумирование» игнорируют температуру и считают верным соотношение.
V1*P1=Vn*Pn=const
Из чего следует, что давление прямо пропорционально плотности газа:
P1/Pn=q1/qn
При этом значение Umax при истечении в вакуум- это объёмный расход в пересчёте на фактическое состояние неподвижного газа в трубе с давлением Р1 перед дроссельным отверстием.
В данном учебнике фактическая скорость газа в дроссельном отверстие не только нигде не рассматривается, но даже не упоминается само понятие «скорость газа» или «скорость газовой струи». Единственной значимой скоростью в учебнике считают «местную скорость звука» при данной температуре и молекулярной массе газа.
Но мне для своих расчётов достаточно и одного объёмно-массового расхода Umax, чтобы свести тяговые характеристики ЖРД в критическом сечение с массовым расходом газа при дросселирование. В результате этого сведения можно получить реальную скорость газовых молекул в критическом сечении дросселирующего отверстия.
Посмотрим к каким результатам приведёт расчёт скорости струи из эксперимента (см.рис.5.) с истечением из ресивера воздуха с избыточным давлением 5 бар, если известен расход газа «по учебнику» и тяга струи по эксперименту. (отчёт по эксперименту в статье см. по ссылке)
https://habr.com/ru/articles/768916/
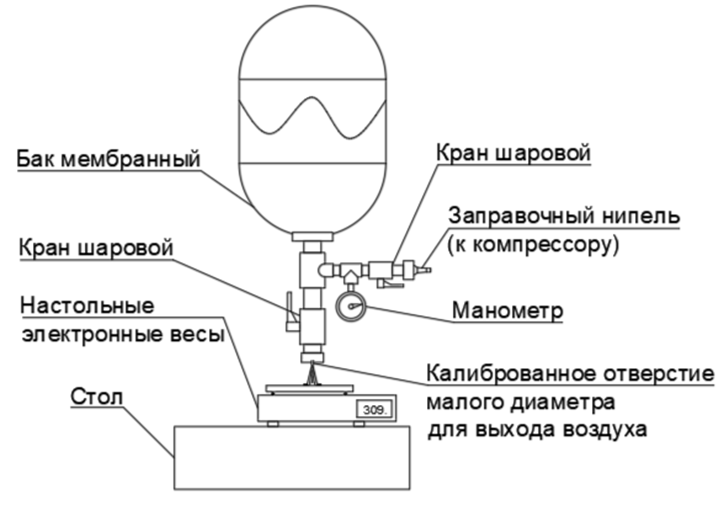
Рис.5. Схема экспериментальной установки для замера силы реактивной тяги струи из отверстия малого диаметра в ресивере под давления.
Исходные данные для расчёта
Отверстие Ф1,5мм, Сила тяги 149г, Т=293К (+20С), дР=5 бар (абсолютное давление б бар)
Вариант -1
Считаем истечение струи на dP=6-1= 5 бар
Umax =0,634*313
Массовый расход из отверстия составит:
G= Umax* q1*Sотв=0,634*313*(5*1,2)*1,766*10^-6=0,0021кг/с
Сила тяги струи Fт = 0,148*9,81=1,45Н
Откуда можем получить расчётную скорость из уравнени.
Fт = dm*v/dt=G*Vcоп
Откуда скорость истечения из отверстия Vсоп:
Vсоп=Fт/G=1,45/0,0021= 690м/с
Расчётная плотность струи в отверстие:
q2=Fт/(Sсоп*Vсоп^2) =1,45/(1,77*10^-6*690^2) =1,72 кг/м3
Расчёт температуры адиабатического расширения:
V2/V1=6/1,72
Р1/Р2=(V2/V1)^1,4 =(6/1,72)^1,4=5,75
Р1*V1=RТ1
Р2*V2=RТ2
Откуд.
(Р1*V1)/ (Р2*V2)= Т1/Т2
Т2=Т1*(Р2*V2)/ (Р1*V1) = 293*(6/1,72)/5,75 =177К
Вариант -2
Считаем истечение струи как в вакуум на dP=6 бар
Umax =0,634*313
Массовый расход из отверстия составит:
G= Umax* q1*Sотв=0,634*313*(6*1,2)*1,766*10^-6=0,0025кг/с
Сила тяги струи Fт = 0,148*9,81=1,45Н
Откуда можем получить расчётную скорость из уравнени.
Fт = dm*v/dt=G*Vcоп
Откуда скорость истечения из отверстия Vсоп:
Vсоп=Fт/G=1,45/0,0025 = 580м/с
Расчётная плотность струи в отверстие:
q2=Fт/(Sсоп*Vсоп^2) =1,45/(1,77*10^-6*580^2) = 2,435 кг/м3
Расчёт температуры адиабатического расширения:
V2/V1=6/2,435
Р1/Р2=(V2/V1)^1,4 =(6/2,435)^1,4=3,534
Р1*V1=RТ1
Р2*V2=RТ2
Откуд.
(Р1*V1)/ (Р2*V2)= Т1/Т2
Т2=Т1*(Р2*V2)/ (Р1*V1) = 293*(6/2,435)/3,534 = 204К
Вариант -3.
Считаем истечение струи на dP=6 бар с коэффициентом расхода для воздуха 0,53 из прошлой статьи.
Umax =0,53*340
Мне больше нравится моя версия истечения воздуха при дросселирование с коэффициентом расход 0,53 и реальной скоростью звука в воздухе по справочнику 340м/с
Тогда Umax= 0,53*340
Массовый расход из отверстия составит:
G= Umax* q1*Sотв=0,53*340*(6*1,2)*1,766*10^-6=0,0023кг/с
Сила тяги струи Fт = 0,148*9,81=1,45Н
Откуда можем получить расчётную скорость из уравнени.
Fт = dm*v/dt=G*Vcоп
Откуда скорость истечения из отверстия Vсоп:
Vсоп=Fт/G=1,45/0,0023 = 630м/с
Расчётная плотность струи в отверстие:
q2=Fт/(Sсоп*Vсоп^2) =1,45/(1,77*10^-6*630^2)= 2,064 кг/м3
Расчёт температуры адиабатического расширения:
V2/V1=6/2,064
Р1/Р2=(V2/V1)^1,4 =(6/2,064)^1,4=4,454
Р1*V1=RТ1
Р2*V2=RТ2
Откуд.
(Р1*V1)/ (Р2*V2)= Т1/Т2
Т2=Т1*(Р2*V2)/ (Р1*V1) = 293*(6/2,064)/ 4,454 = 191К
Вывод из 3-х расчётов:
Все три расчётных варианта дают скорости струи при дросселирование почти в 2 раза больше реальной скорости звука в воздухе.
А вот по температуре в струе все три варианта весьма схожи:
Т2= 177 К , что даёт отношение Т2/Т1=177/293=0,61 при скорости 690м/с.
Т2= 191 К , что даёт отношение Т2/Т1=191/293=0,65 при скорости 630м/с
Т2= 204 К , что даёт отношение Т2/Т1=204/293=0,697 при скорости 580м/с
Все эти температуры близки к отношению Т2/Т1=2/3=0,66 от исходной в ресивере Т1, или падение температуры приблизительно на дТ=0,333*Т1 исходной температуры.
Где реальность — это большой вопрос к экспериментаторам.
Данную температуру сверхзвуковой струи нужно замерять на кромке дросселирующего отверстия перед входом струи во вторичный объём. (см рис.6.)

Рис.6. Положение термодатчика (красный квадрат) через теплоизолирующую прокладку (жёлтая окантовка) за дроссельным отверстием для замера охлаждённой температуры высокоскоростной струи при дросселирование до начала торможения струи с восстановлением температуры.
При этом желательно кольцевую кромку отверстия с термодатчиком отделить термоизолирующей прокладкой от основного массива стенки с отверстием.
Таким образом измеряемая температура на кромке отверстия будет ближе к температуре струи, так как уменьшится изменение её температуры от перетока тепла от тёплой стенки к холодному газу струи.
Что дросселируемый газ в струе имеет очень низкую температуру и холодная струя газа способна охлаждать дросселирующее устройство отлично видно на фото, где газовый редуктор давления обмерзает до заиндевения на тёплой улице при дросселирование газа с высоким давлением из газгольдера в трубу низкого давления к газовому котлу.(см.рис.7.)

Рис.7. Обмерзание газового редуктора при длительном дросселировании газа из газгольдера в трубопровод низкого давления. Газ под высоким давлением в газгольдере тёплый, что видно по отсутствию инея на манометре высокого давления справа. При этом сам редуктор и гофрошланг с газом низкого давления покрыты инеем при плюсовой температуре вокруг.
Расчёт скорости истечения из ЖРД по массовому расходу «по учебнику»
Предельная тяга на критическом сечении для газа при К=1,15 равна 123,4% от Р1 в КС. (см.таб.рис.8.) и статью по ссылке.
https://habr.com/ru/articles/699564/
Рис.8. Фрагмент страницы учебника с данными как по полной тяги ЖРД, так и по отдельным частям конструкции: тяга КС на срезе критического течения КС и тяга сопла Лаваля. При к=1,15 коэффициент расхода равен 0,617 при скорости Vam=1043м/с при Ткс=3800К и плотности газа 9,89кг/м3 при давлении Ркс=100бар в камере сгорания ЖРД (в ресивере). Если считать экспериментальную силу тяги в критическом сечение Fкс=1,234*Р1 согласно таблице из учебника (см.рис.), то согласно закону Ньютона: F=dm*v/dt= q2*S2*V2^2 (1.2) Интересно, что 1,234=2*0,617 То есть коэффициент расхода КС точно соответствует половине коэффициента силы тяги КС. Разница в два раза точно вписывается в двукратное превышение силы реактивной тяги цилиндрической струи от скоростного напора по сечению этой струи. (см. парадокс водяной струи при истечении из бака под давлением). Так как массовый расход G= dm до критического сечения и после одинаковы в силу равномерности и неразрывности течения, то будет верно равенство: G= q1*V1*S1=q2*V2 *S2 (1.3) Подставляем (1.3) в (1.2) и получаем равенство тяги. F=dm*v/dt= G*V2= q1*V1*S1*V2 (1.4) Приравняв формулу динамической тяги реактивной струи к тяге по давлению из таблицы (рис.8.) получаем: F= 1,234*Р1*S2= q1*V1*S1*V2 Из чего получаем значение V2: V2=1,234*Р1*S2/( q1*V1*S1) (1.5) Из ранее приведённого расчёта известно значение: G=dm=q1*S2*Umax= q1*S2* 0,617*Vam (1.6) При подстановке(1.6) в (1.5) получаем: V2=1,234*Р1*S2/( q1*S2* 0,617*Vam) . После сокращения одноимённого значения S2 в числителе и знаменателе получаем: V2=1,234*Р1 /( q1 * 0,617*Vam) (1.7) Для ЖРД нам исходно известны параметры давление Р1=100бар (10^7 Па) в камере сгорания, а также местная скорость звука Vam=1044м/с и плотность газов в КС равная q1=9,89кг/м3. Подставляя в (1.7) известные параметры для КС ЖРД и получаем: V2=1,234*Р1/(0,617*Vam*q1)=1,234*10 000 000/(0,617*1044*9,89) = 1937 м/с Так по методике из уважаемого вузовского учебника «Вакуумная техника» и одного закона Ньютона нам удалось получить расчётом реальную скорость молекул в струе в критическом сечении камеры сгорания ЖРД. V2=Vсоп= 1937 м/с И эта скорость радикально отличается от скорости 1044м/с в этом же месте, но по данным профильного учебника «Теория устройства ракетных двигателей» (А.В. Яскин; Алт. гос. техн. ун-т, БТИ. Бийск: Изд-во Алт. гос.техн. ун-та, 2013 262 с.) Расчёт температуры в критическом сечение камеры сгорания ЖРД Для завершения картины проведём и расчёт температуры струи при адиабатном расширение в критическом сечение до скорости струи Vсоп=1937 м/с. Расчётная плотность струи на выходе из критического сечения рассчитывается из уравнения непрерывности, зная, что массовый расход по сечению равен: G=( q1*S2* 0,617*Vam) Тогд. G=( q1*S2* 0,617*Vam)=q2*Vcоп*S. Откуда получим плотность струи: q2=( q1*S2* 0,617*Vam)/(Vcоп*S2) Что после сокращения общих множителей S2 даст выражение: q2=( q1* 0,617*Vam)/(Vcоп) Подставляем известные значения и получаем значение плотности струи q2: q2 =( 9,89* 0,617*1044)/(1937) = 3,289 кг/м3 Расчёт температуры адиабатического расширения: V2/V1=9,89/3,289 Р1/Р2=(V2/V1)^1,15 =(9,89/3,289)^1,15=3,547 Р1*V1=RТ1 Р2*V2=RТ2 Откуд. (Р1*V1)/ (Р2*V2)= Т1/Т2 Т2=Т1*(Р2*V2)/ (Р1*V1) =Т1*(Р2/Р1)*(V2/V1) = 3800*(1/3,547)*(9,89/3,289) = 3221 К Получили странный результат температуры струи Т2=3221К, что составляет Т2/Т1=3221/3800=0,848 или падение температуры на 15,2%. Что это значит? Получается, что струя поглотила всего 15% внутренней энергии газа при переводе тепловой энергии в кинетическую энергию струи на скорости Vсоп=1937м/с. Данная температура и скорость струи вполне сходится в энергетическом балансе по теплотворности пары керосин- кислород с тепловым выходом Ет=40,5МДж/кг от сжигаемого 1 кг керосина (42 МДж минус 2,5% на испарение криогенных компонетов и работу турбонасосов ЖРД) При этом выхлопные газы при Т3=0К после бесконечного расширения должны иметь максимальную скорость : Мт*Vмах^2/2=Ет Vмах=(Ет*2/Мтоп)^0,5=(40 500 000*2/3,7)^0,5=4672м/с Где Мтоп=3,7кг — это суммарная масса сгоревшего топлива-керосина 1кг и кислорода-окислителя 2,7кг , что в сумме и даёт Мтоп=(1+2,7)=3,7 кг продуктов сгорания в выхлопной струе из ЖРД. Доля кинетической энергии по скорости Vсоп в струе в критическом сечении составит от максимальной Vmax: (Vсоп/Vmax)^2 = (1937/4672)^2 =0,1719 или 17,2% Тогда температура должна быть: Т2е=3800*(1-0,1719)=3146 К А это уже вполне близко к полученной ранее температуре 3221К Относительная погрешность температур составляет величину в отношении Т2/Т2е : Т2/Т2е =3221/3146=1,024 или всего 2,4%. Вполне достойный результат у нас получился. Правда, заметна сильная разница в долях преобразования внутренней энергии газов в кинетическую энергию при дросселирование из ЖРД (17,2%) и при дросселировании холодного воздуха из ресивера при давлении 6 бар (33% по модели срабатывания 1/3 всей внутренней энергии в скорость в одном направлении). Такое отличие процентов трансформации внутренней энергии в кинетическую при дросселирование связано с разницей в показателях адиабаты к=1,15 (для горячих газов в ЖРД) и к= 1,4 (для холодного сжатого воздуха в ресивере). В целом данный расчёт скорости потока в ЖРД своими результатами хорошо соотносится с ранее проведёнными расчётами в статье про ЖРД ( https://habr.com/ru/articles/699564/ ), хотя здесь и там расчёты велись из разных исходных теоретических предположений. Заключение: За что я люблю современную науку, так это за её местечковую раздробленность. В рамках ограниченных задач отрасли вы можете писать чистую экспериментальную правду, так как никто из коллег-смежников читать и проверять этого не будет. В науке не принято лезть в чужие области специализации, так что никто не читает учебники соседних разделов, даже если обсуждаемые вопросы практически совпадают. Так произошло с учебником про ЖРД одного технического ВУЗа и учебником про «Вакуумную технику» из другого вуза. А вот сведя вместе два уважаемых ВУЗовских учебника мы получили удивительный результат, который ни один из учебников не мог в явном виде представить, чтобы не замарать «честь мундира» или не уронить «честь научной школы». То есть мы получили реальную скорость газов в критическом сечении КС ЖРД при дросселирование газов из КС в вакуум. При этом полученная нашим расчётом скорость радикально отличается от параметров скорости газа в критическом сечении КС согласно учебнику по ЖРД. Так по нашему расчёту скорость истечения горячих газов в критическом сечении КС ЖРД получилась V2=1937м/с, что почти в 2 раза больше расчётной местной скорости звука в КС ЖРД, равной Vam=1044м/с. И это именно скорость в самом критическом сечение КС, ещё до разгона по соплу Лаваля. Отношение скоростей в критическом сечение составляет величину: V2/Vam=1937/1044=1,855 Выходит, что преподаватели и профессора ВУЗов, а также академики РАН десятки лет искренне обманывают на лекциях будущих инженеров, внедряя им в головы ошибочные знания о фундаментальных основах реальной физики.