
HP-35 стал примером чрезвычайно привлекательного, миниатюрного и революционного продукта. Карманные калькуляторы с четырьмя функциями уже были в продаже [раньше «карманной» или «ручной» (hand-held), или «переносной», называли электронику, достаточно маленькую, чтобы помещаться в руке и быть портативной — до того, как вся техника стала такой / прим. перев.]. Мало кто мог представить себе машину, способную производить научные расчёты и поместиться в карман рубашки, но многие уже начинали мечтать о такой. HP-35 был разработан компанией Hewlett-Packard, находившейся в Пало-Альто, Калифорния, по адресу 1501, Пэйдж-милл-роуд, и выпущен на рынок в 1972 году. Это был первый полнофункциональный научный калькулятор размером с карман рубашки. Это изобретение произвело революцию в профессии инженера, позволив ему выполнять почти мгновенные и чрезвычайно точные научные расчёты дома, в офисе или «в поле». HP-35 стал инновационной кульминацией механического дизайна, передовой технологии, разработки алгоритмов и приложений — всё это для того времени было уникальным.
Многие из нас мнят себя изобретателями, но реально нам надо фокусироваться на «инновациях» — изготовлении вещей, нужных другим людям, таких, которые они захотят купить. Исследования должны поддерживать разработку конечного продукта. Если в результате появляется что-то новое, то, возможно, появится и достойное патента изобретение. Многие инженеры начинают разработку изнутри, с железа, с двигателя, а потом обустраивают его корпусом. Однако анализ наиболее успешных продуктов за последние десятилетия показывают, что их начинали разрабатывать снаружи; внешний вид и ощущения от использования идут в приоритете перед детальными инженерными разработками.
Во время разработки настольного калькулятора HP-9100, старшего брата HP-35, я отвечал за разработку алгоритмов, способных уместиться в архитектуре, предложенной внештатным изобретателем Томом Осборном. Том принёс в HP схему, работающую с четырьмя функциями и плавающей точкой, ставшую основой архитектуры 9100. Предлагаемая методология алгоритмов была взята у калькулятора Athena, разработанного Малькольмом Макмилланом, также ответственным за калькулятор с фиксированной точкой и трансцендентными функциями. Мне пришлось прочесть очень много литературы, чтобы понять технику различных типов вычислений, многим из которых уже более 1000 лет. Хотя в Wang Laboratories использовали схожие методы подсчётов, в своём исследовании я обнаружил исторические примеры, самый старый из которых датируется аж 1624-м годом — что отменяет патенты Wang Laboratories.

Исследование помогло освоить трансцендентные функции (показательную функцию, логарифм и тригонометрические функции) путём использования алгоритмов, удовлетворяющих нужды пользователя и укладывающихся в ограничения железа. Такой подход оказался бесценным во время разработки НР-35, вплоть до использования 12-значных констант для генерации функций, чтобы уменьшить отклонения до единички в 11-м десятичном разряде.
Над выбором алгоритмов для НР-35 мы размышляли очень тщательно. Степенные ряды, разложение многочленов, непрерывные дроби, многочлены Чебышёва — всё это рассматривалось для применения в расчётах трансцендентных функций. И всё это было слишком медленным из-за количества умножений и делений, требовавшихся для поддержки точности вплоть до десятого разряда на предлагавшемся промежутке в двести степеней десяти. Обобщённым алгоритмом, лучше всего подошедшим под требования скорости и эффективности программирования для НР-35, стал метод итеративного псевдоделения и пвседоумножения, впервые описанный в 1624 году Генри Бригсом в труде Arithmetica Logarithmica, а позже — Вольдером и Меггитом. Алгоритм того же типа ранее использовался в настольных калькуляторах НР.
Кроме того, в результате исследования для разработки настольного калькулятора НР-9100 было предложено использовать обратную польскую запись в качестве основы разработки НР-35. Это повлияло на все аспекты разработки — от количества клавиш до архитектуры внутренней логики. Обратная польская запись требует, чтобы оператор вводился после операндов, в результате чего становятся ненужными скобки. Это позволило вводить данные с помощью меньшего числа нажатий клавиш, а также упростить железо.
Проект калькулятора начался буквально как попытка создать научный калькулятор, который уместился бы в карман рубашки Уильяма «Билла» Хьюлетта. После разработки настольного научного калькулятора НР-9100 в середине 1960-х, Билл стал одержим идеей того, что НР должна разработать калькулятор с теми же возможностями, умещающийся в его карман рубашки. Раз в несколько месяцев он появлялся в лаборатории здания 1U и спрашивал, как идёт его любимый проект. Он часто обращался и лично ко мне, поскольку я занимался исследованиями архитектур, подходящих для научных алгоритмов, использованных мною в НР-9100.
Хотя плотность полупроводников с каждым годом увеличивалась, биполярные транзисторы не смогли бы подойти для нашего проекта — они были слишком большие и потребляли слишком много. МОП-структуры (металл-оксид-полупроводник; англ. metal-oxide-semiconductor, или MOS) обещали высокую плотность и низкое потребление, но всё ещё были на начальных стадиях разработки. Но это не остановило Хьюлетта от того, чтобы поручить группе промышленной разработки лаборатории HP набросать несколько идей, ключевых моментов раскладки, и т.п., способных поместиться в кармане рубашки. Лаборатория твердотельной электроники также работала над светодиодными дисплеями с низким потреблением на основе схем с биполярными транзисторами. От различных изготовителей США и Японии я собрал большую коллекцию полупроводниковых архитектур, выполнявших простые вычисления с четырьмя функциями. Большая часть из них была биполярной, но некоторые производители уже пробовали разрабатывать МОП-схемы с несколькими сотнями транзисторов на чипе. В конце 1970 всё резко поменялось, когда Fairchild Semiconductor продемонстрировала управляющему отделом в HP Тому Уитни и мне архитектуру pMOS, выглядевшую весьма подходящей в кандидаты на работу с научными алгоритмами. Двоично-десятичный сумматор (binary-coded decimal, BCD) и поддержка нескольких 20-разрядных слов в регистрах сдвига с циркуляцией информации были весьма эффективными с точки зрения размера и энергопотребления чипа. У Fairchild не было патента на эту архитектуру, поскольку они, якобы, взяли её у Sweda, производителя электронных касс. Они собирались предлагать этот набор микросхем в качестве платформы для калькуляторов с четырьмя функциями и фиксированной точкой.
Примерно две недели я изучал изменённую архитектуру, основанную на том, что я увидел у Fairchild, и решил, что мне понадобятся только регистры на 13 разрядов (56 бит) и слова длиной в 11 бит; позже их сократили до 10 бит, используя мнимый условный переход. Уменьшение схемы на 10% было довольно значительным. Тринадцати разрядов должно было хватить для точности в 10 разрядов, с одним разрядом для переполнения или переноса и двумя разрядами защиты. Слово можно было отображать либо в виде мантиссы с двумя цифрами экспоненты, либо в виде результата переменной длины с фиксированной точкой. У продукта должен был быть арифметический чип и чип регистров, схемы контроля и хронометража, и несколько чипов ROM. Как часто человеку выпадает шанс разработать набор микроинструкций?
Fairchild решили, что не будут делать специальную схему на заказ для НР, поэтому мы вместе с управляющим отделом Томом Уитни и директором лаборатории Полом Стофтом отправились к Биллу Хьюлетту, надеясь, что он обрадуется нашей комбинации из технологии и архитектуры, способной разместиться в его кармане. Мы рассказали ему, что нам нужно будет заказать разработку нескольких новых чипов pMOS. И итоговая стоимость продукта точно будет гораздо большей, чем $100, за которые тогда продавались калькуляторы с четырьмя функциями. Хьюлетт не был уверен, что получит хороший отклик от разработки стоимостью в миллион долларов, поэтому мы использовали существующий бюджет отдела исследований и разработок, а Хьюлетт связался с центром аналитических разработок SRI, чтобы поручить им независимое исследование рынка. SRI работал много месяцев, изучал различные фокус-группы, и т.п., и выдал ответ: то, что задумала НР, «не представляется возможным оценить».
Первичными целями при создании НР-35 были:
- Калькулятор размером с карман рубашки.
- Возможность подсчёта трансцендентных функций (тригонометрических, логарифмических, экспоненциальных) и даже (простого) квадратного корня.
- Выполнение указанных операций в промежутке двухсот степеней десятки, что позволяло представлять числа от 10-99 до 9,999999999 x 1099.
- Дисплей должен состоять из 15 семисегментных светодиодных числовых индикаторов с подходящим положением для десятичной точки, которые должно быть видно при солнечном свете.
- У калькулятора должно быть пять регистров для хранения констант и результатов, четыре из которых составляли операционный стек — такая возможность в то время была не у всех компьютеров.
- Четыре часа работы на перезаряжаемых батареях.
- Цена, доступная инженерам и учёным.
Как должен был выглядеть НР-35? Он должен был быть размером с карман — а значит, лёгким и простым в переноске. Какие ему нужны были кнопки, как они все разместятся при таком ограничении размера? Примут ли пользователи кнопки префикса и суффикса? Как разместить кнопки так, чтобы ими было удобно пользоваться? Можно ли избежать случайного нажатия соседних кнопок? Батарея должна была работать по нескольку часов без перезарядок. Дисплей должен был быть читаемым на расстоянии вытянутой руки и при ярком солнечном свете.
Промышленная разработка НР-35 была в новинку не только для Hewlett Packard, но и для всей индустрии электроники в целом. Обычно механические и электрические компоненты продукта определялись до того, как разрабатывался его внешний вид; НР-35 пошёл по противоположному пути.
Поскольку калькулятор должен был умещаться в кармане рубашки, размер был доминирующим ограничением разработки. Сразу же было установлено ещё несколько параметров. Калькулятору потребуются три батареи для достижения заявленного времени работы, с высокоэффективным преобразователем постоянного тока на предполагаемом напряжении полупроводников и с соответствующими требованиями к питанию. На основе разработок предыдущих, настольных калькуляторов, у НР-35 решено было сделать 35 клавиш (очевидно, не так ли, что название калькулятору придумали после разработки?), а также пятнадцатизначный светодиодный дисплей с экспоненциальной записью, десятичной точкой и знаками для мантиссы и экспоненты.
Промышленное проектирование началось с исследования клавиатуры, корпуса, общей концепции формы. При помощи скетчей и трёхмерных моделей было изучено несколько основных форм-факторов, что позволило хорошо оценить рассматриваемые формы и размеры. С точки зрения инженерной психологии самым критичным моментом была клавиатура. Проблема была в том, как разместить 35 клавиш на площади размером 6,5 см х 11,5 см, сохраняя возможность работать с клавишами, не нажимая более одной за раз. Стало очевидно, что от промышленного стандарта в 19 мм между центрами клавиш придётся отказаться.
Успешным компромиссом стало использование расстояния в 17 мм между центрами цифровых клавиш, и 13 мм для остальных. Это стало возможным после уменьшения размеров клавиш, что увеличило расстояние между ними. Клавиши поделены на группы согласно функциям. Группы разделены по размеру, контрасту, цвету и расположению. Цифровые клавиши, как наиболее часто используемые, сделаны более крупными и у них наибольший контраст. Их обозначения нанесены непосредственно на них самих. Следующая группа клавиш по частоте использования выделена голубым цветом. Клавиша ввода и арифметические клавиши выделены в этой группе тем, что их обозначения нанесены на сами клавиши. Наименее часто используемые клавиши имеют наименьший контраст, а их обозначения нанесены на панели над клавишами.
Требования к клавиатуре НР-35 были особенно сложными. Она должна была быть надёжной, недорогой, с невысокими клавишами, приятная на ощупь. Решение было основано на том факте, что у изогнутых металлических полосок, закреплённых на концах, могут быть два стабильных состояния. При нажатии клавиши выдавали тактильную обратную связь, похожую на ту, что была у детской игрушки-сверчка [по-видимому, какая-то известная среди детей в США того времени игрушка / прим. перев.]. В НР был разработан особый пружинный контакт высотой в 3 мм. Тактильное ощущение клавиш давало чёткое понимание момента, в который происходил контакт.
Корпус НР-35 был разработан с учётом инженерной психологии и важности внешнего вида. Края калькулятора особой формы позволяют удобно держать его в одной руке. Также они позволяют ему легко входить в карман. Клавиатура и дисплей отклонены вверх, чтобы их проще было видеть при настольном использовании. Верхняя часть корпуса светлее нижней — из-за этого продукт кажется тоньше, чем он есть на самом деле. Кажется, будто он парит, когда смотришь на него при обычном настольном использовании. Использование дополняющих друг друга текстур сильно повлияло на его общий элегантный вид. Текстура корпуса даёт нескользящую поверхность, что важно, когда его держат в руке. Команда промышленного дизайна под руководством Эда Лильенвола проделала выдающуюся работу, ничего не зная о начинке продукта.
В то время об электронной начинке калькулятора существовали лишь общие сведения. Разработка и упаковка всех необходимых электрических и механических компонентов в крохотный продукт стала титанической задачей для разработчиков электроники и механических частей и промышленных дизайнеров. НР-35 не появился бы на свет без потрясающих рабочих взаимоотношений между лабораторией разработки, командами промышленного дизайна, производства и инструментальной оснастки. У всех работавших над проектом была общая цель сохранить изначальный размер и форму, в результате чего было придумано множество инженерных инноваций. Многие проблемы, встреченные при разработке, можно было бы легко решить привычными способами, но тогда главные цели не были бы достигнуты, и продукт был бы менее привлекательным.
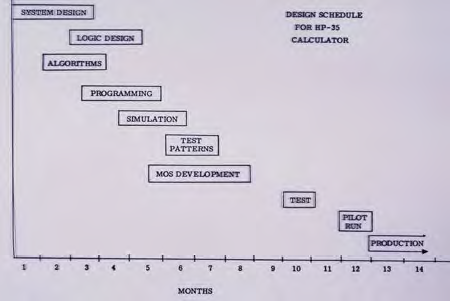
График разработки НР-35
На ранних этапах планирования НР-35 было очевидно, что для него потребуются новые дисплейные технологии. Существовавшие тогда светодиоды потребляли слишком много энергии и слишком много стоили. В НР разработали пятизначное табло, экономящее энергию и стоимость благодаря встроенным пластиковым сферическим линзам напротив каждой цифры. Эффективность светодиодов повышается при использовании малого коэффициента заполнения вместо постоянного тока. В НР-35 энергия хранится в индукторах и подаётся на светодиоды. Такая технология позволяла активно использовать мультиплексирование; цифры сканировались по одной, один сегмент за другим. Обширные проверки на надёжность показали незначительное изменение интенсивности после нескольких годов пульсации тока с коэффициентом заполнения в 0,1%. Читаемость дисплея даже на ярком солнце была настолько важна, что отдельные сегменты немного изменили, добавив небольшие засечки с левого края верхней и нижней полос. Каждый сегмент также изменили так, чтобы периметр был сопоставим с отношением площадей, чтобы добиться однородной визуальной интенсивности.
Дисплей НР-35 был устроен аналогично десятизначным дисплеям настольных калькуляторов НР. Он состоял из 15 семисегментных знаков и десятичных точек. Результаты в промежутке от 1010 до 10-2 всегда демонстрировались в виде чисел с плавающей точкой, каковая была соответствующим образом размещена на дисплее, а степенное поле оставалось пустым. Вне этого промежутка НР-35 показывал результат в экспоненциальной записи с десятичной точкой справа от первой значимой цифры и соответствующей степенью 10, расположенной с правого края дисплея. Для повышения читаемости для десятичной точки был выделен собственный сегмент.
В НР-35 было пять схем MOS/LSI (metal-oxide semiconductor/large-scale integration; МОП на большой интегральной схеме): ROM, арифметическая схема, схема регистров (A&R), управляющая схема и схема хронометража (C&T). Логическую схему разработали Фрэнс Роуд и Чан Тан из HP Laboratories, а электронные схемы разрабатывали и изготавливали два сторонних производителя. Три сделанных на заказ биполярных схемы также были разработаны в HP Laboratories и изготовлены подразделением компании в Санта-Кларе — двухфазный формирователь тактовых импульсов, генератор тактовых импульсов и анодного напряжения для светодиодов, и катодный драйвер светодиодов. НР-35 собирался на двух печатных платах. Верхняя содержала дисплей, формирователи и клавиатуру. Нижняя, более мелкая, содержала всю логику на МОП, формирователь тактовых импульсов и источник питания.

Системная архитектура НР-35
Выбор батареи и разработка источника питания были нетривиальными задачами; для увеличения эффективности преобразователя постоянного тока был использован стек из трёх батарей. Эффективность однотранзисторного преобразователя была выше 80%, что обеспечивало задачу работы от батареи в течение четырёх часов. Как и в остальных аспектах дизайна, в этой разработке участвовали лучшие люди; Чу Йен, доктор наук, работавший в HP Laboratories, добился такой великолепной эффективности, даже несмотря на необходимость подачи различных напряжений (+7,5 В, +6 В и -12 В, необходимые для работы МОП и биполярных схем калькулятора). Схожие концепции использовались для сетевого адаптера/зарядного устройства.
Данные в калькуляторе организованы на последовательной архитектуре. Такая организация минимизирует количество контактов каждой схемы и между схемами, что экономит место и стоимость, увеличивая надёжность. Каждое слово состоит из 14 двоично-десятичных цифр, или 56 бит. Десять из 14 цифр отводятся мантиссе, одна — знаку мантиссы или для переполнения во время вычислений, две экспоненте, и одна — знаку экспоненты. Три последних также выполняют дополнительную функцию разрядов защиты.
Три основных шины соединяют МОП-схемы. По одной идёт сигнал синхронизации по словам (SYNC), создаваемый счётчиком, имеющим 56 состояний, на чипе контроля и хронометража. По другой шине инструкции (Is) последовательно передаются из ROM в чип управления и хронометража или в чип арифметики и регистров. Третий сигнал шины, выбор слов (WS), служит селекторным сигналом, создаваемым чипом C&T или ROM. Он выдаёт арифметическому модулю часть слова, благодаря чему существует возможность проводить операции только над одной частью числа, например, над мантиссой или экспонентой. Схема C&T выполняет основные неарифметические или вспомогательные функции в калькуляторе. Среди них — опрос клавиатуры, отслеживание статуса системы, синхронизация, изменения адресов инструкций.
Клавиши расположены в пять столбцов и восемь рядов. C&T чип её постоянно опрашивает. Когда между рядом и столбцом появляется контакт, соответствующий код передаётся в ROM. Этот код — начальный адрес программы, находящейся в ROM, обслуживающей эту клавишу. Ложные повторные нажатия и отключение клавиши реализованы через программируемые задержки.
Во всех цифровых системах используются биты состояния, или флаги, отслеживающие произошедшие события. В НР-35 есть 12 битов состояния, расположенных на чипе C&T. Их можно установить, сбросить, и опросить при помощи микроинструкций. Адреса ROM обновляются на чипе C&T и последовательно отправляются в ROM. Во время выполнения ветвящейся инструкции проверяется соответствующий сигнал — арифметический перенос или бит состояния — чтобы определить, нужно ли следующим шагом выбирать увеличивающийся адрес или адрес ветвления.
Одной из самых главных особенностей последовательной работы была возможность работать над единственной цифрой или над несколькими цифрами числа, пока они побитово проходили через арифметический модуль. Этот уникальный дизайн свёл до минимума архитектуру, что позволило вообще создать НР-35 в то время. При этом получилось совместить элементарные процедуры сложения и сформировать чрезвычайно мощные подпрограммы, способные полностью выполняться менее, чем за секунду.
В качестве аналогии можно представить себе лошадиные бега. Допустим, мимо трибун в единицу времени пробегает только одна «лошадь», то есть бит. Тогда после прохождения каждых четырёх лошадей, или битов, происходят подсчёты, связанные с этой цифрой. Сигнал выбора слова соответствует количеству цифр, или групп лошадей, в последовательности, или временному промежутку, за который проходит полный цикл работы над словом.
Заранее запрограммированные математические функции хранятся в трёх чипах ROM, каждый из которых содержит 256 инструкций по 10 бит каждая. В любой момент времени используется только один из этих чипов, а остальные чипы отключаются.
Схемы для арифметики и регистров выполняют инструкции последовательно по битам. Большая часть арифметических инструкций включается по сигналу выбора слова. Данные, которые необходимо вывести, отправляются на формирователи сигнала светодиодов, а несущая линия передаёт информацию обратно в чип C&T. Двоично-десятичный вывод двунаправленный, и способен передавать цифры в чип A&R, и из него. Схема A&R разделена на пять областей: хранение инструкций и схемы расшифровки, хронометрическая схема, семь 56-битных регистров, сумматор/вычитатель, и декодер дисплея. Три регистра — рабочие. Один из них и три из оставшихся четырёх регистров формируют стек из четырёх регистров. Седьмой регистр независимый, служит для хранения констант. Между регистрами есть множество связей, позволяющих выполнять такие инструкции, как обмен, передача, ротация стека, и т.п.
Преимущество последовательной по битам структуры в том, что для внутренних связей достаточно одного шлюза на линию. Передача данных в/из стека или в/из регистра константы всегда осуществляется целыми словами. Все остальные арифметические инструкции управляются по сигналу выбора слова. Поэтому возможно, например, обмениваться полями степени двух регистров, или складывать две любые соответствующие цифры двух десятичных чисел. Сумматор/вычитатель вычисляет сумму или разницу между двумя десятичными числами. У него есть два входа для данных, место для хранения положительного или отрицательного переноса, и для суммы и вывода переносов.
В трёх первых тактах сложение чисто двоичное. На четвёртом такте проверяется двоичная сумма, и если ответ превышает 1001 (девять), тогда сумма подправляется до десятичной добавлением 0110 (шесть). Потом результат добавляется в четыре последних бита принимающего регистра, и перенос сохраняется. Похожая коррекция проводится для вычитания. Информация о переносе всегда передаётся, но записывается чипом управления и хронометража только во время передачи последнего бита в сигнале выбора слова.
При разработке таких сложных интегральных схем, как C&T, A&R и чипы ROM, нужно с самого начала ответить на два вопроса: как проверять дизайн, и как проверять полученную интегральную схему. На первый вопрос есть два ответа. Один — сделать макетную плату и сравнить её работу с нужной операцией, второй — провести компьютерную симуляцию схемы.
При разработке МОП-схем для НР-35 был выбран подход компьютерной симуляции. Было решено, что реальная макетная плата не станет точной моделью конечных схем, а при помощи компьютерной симуляции можно сэкономить 2-3 месяца разработки, поскольку люди смогут работать параллельно, а не последовательно, как в случае с макетом.
Программу для произвольных симуляций как раз разработал Джим Дьюли из НР. Её использовали для проверки каждого шлюза, каждой схемы, каждого чипа, и, наконец, всех чипов вместе. Для вывода каждого шлюза было написано алгебраическое уравнение, как функция от его ввода. В результате на каждый такт необходимо было вычислять большой набор алгебраических уравнений. Инженерам была доступна распечатка результатов, чтобы можно было наблюдать за работой любого шлюза или отложенными выводами, так, как это делается с осциллоскопом. В этом смысле компьютерная симуляция была гораздо лучше реального макета.
Из-за большого количества уравнений, которые требовалось решать каждый такт, проверочная программа общего назначения была слишком медленной, и не справлялась с проверкой алгоритмов, разработанных для НР-35. Для этого использовалась симуляция более высокого уровня, и в ней нужно было задавать только функции ввода/вывода каждой подсистемы. Это было достаточно быстро для проверки всех алгоритмов, даже для трансцендентных функций. Если что-то шло не так, всегда можно было остановить выполнение программы и пройти по шагам, пока проблема не была найдена. Проблему можно было решить, просто изменив парочку перфокарт — преимущество, отсутствовавшее у макетной платы.
Использование симуляции оказалось очень успешным. Оно сэкономило кучу времени не только на разработку логики, но и на создание проверочных последовательностей, используемых для тестирования итоговых интегральных схем. После того, как симуляция работает без сбоев, для каждого ввода задаётся последовательность действий, причём таким образом, чтобы задействовать практически все элементы схемы. Запустив программу и записав весь ввод и вывод, можно получить полную проверочную последовательность, готовую для итоговой проверки интегральной схемы.
В это время были сделаны оценки времени выполнения программ, и стало ясно, что с использованием структуры, последовательной по битам, можно создать такой набор схем, который сможет выполнять все вычисления за требуемое время, не превышающее секунды. Более того, адрес команды и слово команды тоже могут быть последовательными по битам.
Сложность алгоритмов привела к необходимости многоуровневого программирования. Это означало, что у калькулятора должна была быть возможность исполнения подпрограмм, а также особые флаги, обозначающие состояние и разделение различных программ. В НР-35 опрос и ветвление битов флага или при арифметическом переносе осуществляется отдельной инструкцией, и не включается в качестве части в каждую инструкцию. Это позволяет сильно понизить длину слова инструкции, совсем немного уступив в скорости.
Для генерации трансцендентной функции, например, arctanh(x) — ареакотангенса — требовалось написать несколько уровней подпрограмм. Однако вызов подпрограмм осуществлялся через установку флагов, поэтому первостепенную важность имели блок-схемы и система управления. Крис Клэр позже описал эту систему как алгоритмический автомат (Algorithmic State Machine, ASM). Даже простые функции синуса или косинуса используют подпрограмму вычисления тангенса, а затем подсчитывают синус через тригонометрические процедуры. Такие сложные манипуляции были необходимыми для минимизации количества уникальных программ и их шагов, и для того, чтобы остаться в пределах трёх ROM-чипов на 750 слов.
Набор арифметических инструкций был разработан специально для десятичного калькулятора с трансцендентными функциями. Основные операции осуществляются сумматором/вычитателем с обратным кодом, у которого есть каналы передачи данных к трём регистрам, использующимся для хранения.
Определение точности НР-35 по сложности сравнимо с его алгоритмами. У калькулятора есть внутренний округлитель для 11-го разряда. При сложении, вычитании, умножении, делении и взятии корня точность равна половине итога в 10-м разряде. При подсчёте трансцендентных функций многие из этих элементарных подсчётов осуществляются с накоплением ошибок округления. При вычислении синуса предварительно производится деление, умножение и вычитание, а потом ещё два деления, умножение, сложение и извлечение квадратного корня. Ошибки округления в этих вычислениях накапливаются, что добавляет общую ошибку в основной алгоритм.
Точность и разрешение иногда конфликтуют друг с другом. К примеру, вычитание из 1,0 числа 0,9999999999 даёт только одну значащую цифру. Это становится очень важным, к примеру, при вычислении косинусов углов, близких к 90°. Косинус 89,9° можно было бы посчитать более точно, найдя синус 0,1°. Точно так же синус 1010 тратит все десять значимых цифр для описания угла, поскольку все целые круги отбрасываются.
Разработка НР-35 была «мечтой». Это был идеальный момент совпадения — только появились технологии изготовления кремния высокой плотности, у меня были все алгоритмы для HP-9100, а у клиентов — запрос на портативные вычисления. Физическое воплощение проекта рождалось на чертёжной доске многие месяцы. Когда я увидел архитектуру «лошадиных бегов», разработанную на pMOS, я сразу понял, что она нам подойдёт. Fairchild Semiconductor активно рекламировала её для калькуляторов с четырьмя функциями и фиксированной точкой. И хотя она не совсем идеально подходила для нужных мне алгоритмов, я мог заставить её работать. Когда Fairchild решила не исправлять схему и не налаживать производство для НР, я сказал Тому Уитни, что мы сможем сделать всё сами, отдав редизайн в AMI и Mostek. Том убедил Пола Стофта и отслеживал проект до конца.
Я очень радовался возможности разработать свой собственный набор инструкций, настоящий компьютер с сокращённым набором команд (reduced instruction-set computer, RISC), поскольку в 1970-м на чипе невозможно было разместить достаточно кремния. Каждая инструкция должна была активировать какую-то комбинаторную логику, только то, что необходимо для работы. Необходимым злом были инструкции, выполняемые по нажатию клавиши, поскольку они использовались только один раз на каждую функцию. Сначала существовало две ветвящиеся инструкции, одна — условный переход, выполняющаяся после операции, которая могла выдать перенос или привести к изменению флага, другая — безусловный переход. Поскольку они увеличивали ширину слова в ROM, я решил использовать только условный переход, что гарантировало, что по умолчанию я никогда не буду использовать её вслед за операцией назначения условия. Это уменьшило размер ROM на 10%.
Известно, что когда мы пришли к Хьюлетту и рассказали ему, что мы можем это сделать, он решил подстраховаться и заказать у SRI маркетинговое исследование. Для оплаты разработки в $1 млн он использовал деньги лаборатории.
В процессе прототипирования мы устраивали несколько конкурсов по «подбору ребёнку имени», но Хьюлетт назвал калькулятор «НР-35» по количеству клавиш. В конце 1971 мы собрали несколько прототипов калькулятора и раздали их известным учёным. Одним из первых был декан инженерной школы Стэнфорда, Фред Терман, человек, ответственный за сотрудничество Билла Хьюлетта и Дэйва Пакарда. Он был поражён, и всё искал пуповину, которая должна была соединять калькулятор с большим компьютером, выполнявшим все эти вычисления. И что бы вы думали — именно он нашёл первый баг. Он ввёл угол в 90 градусов и нажал клавишу TAN. Модуль начал мигать, поскольку алгоритм попытался выполнить деление на ноль. Мне пришлось ввести специальную процедуру, которая показывала на экране 1099, обозначавшую бесконечность. А лауреат нобелевской премии Чарлз Таунс был так впечатлён, что назвал калькулятор «восьмым чудом света».
НР-35 был представлен без особой шумихи и продавался по $395 по обычным каналам продаж. Но о нём начали говорить, и заказы быстро превысили предложение. Говорили, что некоторые покупатели готовы были накинуть $100, лишь бы ускорить выполнение их заказа. Открылись и другие каналы продаж — продукцию НР, которую обычно продавали технические представители, начали распространять через универмаги. Было невероятно странно видеть выстроившиеся в ряд НР-35 на прилавке магазина Macy’s. Первая партия в 100 000 штук должна была растянуться на полгода; через несколько месяцев план увеличили вдвое. Но даже после начала производства Билл Хьюлетт не был уверен, что проект станет успешным. Однажды за обедом я упомянул, что мы получили от General Electric запрос о цене на 100 000 штук. Он сказал: «Это, наверное, ошибка, зачем им столько?» Я ответил: «Может, они покупают по штуке для каждого из их инженеров». Билл ответил: «Им нужно просто купить несколько штук, и пусть их инженеры одалживают калькуляторы друг у друга».
Тщательное внимание к деталям в каждом аспекте НР-35, от времени жизни батареи, формы семисегментного дисплея до расположения клавиш, окупило себя. Можно было предвидеть, что НР-35 станет успешным, поскольку его хотели приобрести все инженеры. Компания Dietzgen, производившая логарифмические линейки, закрылась примерно через год после появления карманного научного калькулятора. В школах всего мира начали задавать вопросы о том, можно ли приносить НР-35 на урок? Многих учителей он ставил перед дилеммой — позволить ли ученикам, которые могут потратить на калькулятор $395, приносить его? А как же контрольные работы? Некоторые школы запретили пользоваться калькуляторами во время тестов, другие их выдавали. Вскоре на многих курсах калькуляторы стали обязательными, поскольку учитель теперь мог задавать «реальные задачи» — такие, ответ на которые не был целочисленным.
И мир изменился навсегда.
Источник


