Авторы — Кынев С.М., Гончаров Р.К., Иванова А.Е., Самсонов Э.О
Научные сотрудники ООО «СМАРТС-Кванттелеком»
«Генерация случайных чисел слишком важна, чтобы оставлять её на волю случая».
Роберт Кавью
Случайные числа являются важнейшим ресурсом в большом числе практических приложений. Последовательности случайных чисел применяются в системах безопасности, криптографии (в том числе в квантовой криптографии), в научных исследованиях (статистике, моделировании различных систем и процессов), а также в играх.

Генераторы случайных чисел (ГСЧ) можно формально разделить на две категории: псевдослучайные и аппаратные. Генерация псевдослучайных чисел основана на математических алгоритмах, позволяющих получать каждое последующее число путем математического преобразования предыдущего числа согласно заданному алгоритму. Однако, зная предыдущие числа и математический алгоритм, можно предсказать всю последовательность. Алгоритмы генерации псевдослучайных чисел хорошо описаны в статье.
Аппаратные или физические ГСЧ, в свою очередь, можно разбить на две категории: классические и квантовые генераторы.
В классических ГСЧ источником энтропии служит процесс, который описывается законами классической физики. Детерминированность таких процессов дает потенциальную возможность злоумышленнику воспроизвести генерируемые классическим аппаратным ГСЧ последовательности. Квантовые генераторы случайных чисел (КГСЧ) в качестве физического источника энтропии используют квантовые процессы, которые сами по себе имеют вероятностную природу. Следовательно, КГСЧ может являться генератором истинно случайных числовых последовательностей, подходящих в том числе и для криптографических приложений.
Применение источников энтропии, построенных на основе эффектов квантовой
оптики, является одним из наиболее перспективных подходов к построению генераторов последовательностей недетерминированных случайных чисел, что
обеспечивается фундаментальной вероятностной природой квантовых процессов. На Хабре уже пытались собирать квантовый генератор случайных чисел. Вообще такие генераторы могут быть основаны на разных эффектах: регистрация фотонов в различных оптических модах, время обнаружения фотонов, счет фотонов в импульсе, фазовые шумы лазера, суперлюминесценция, рассеяние и т. д. Каждое такое устройство имеет как преимущества, так и недостатки.
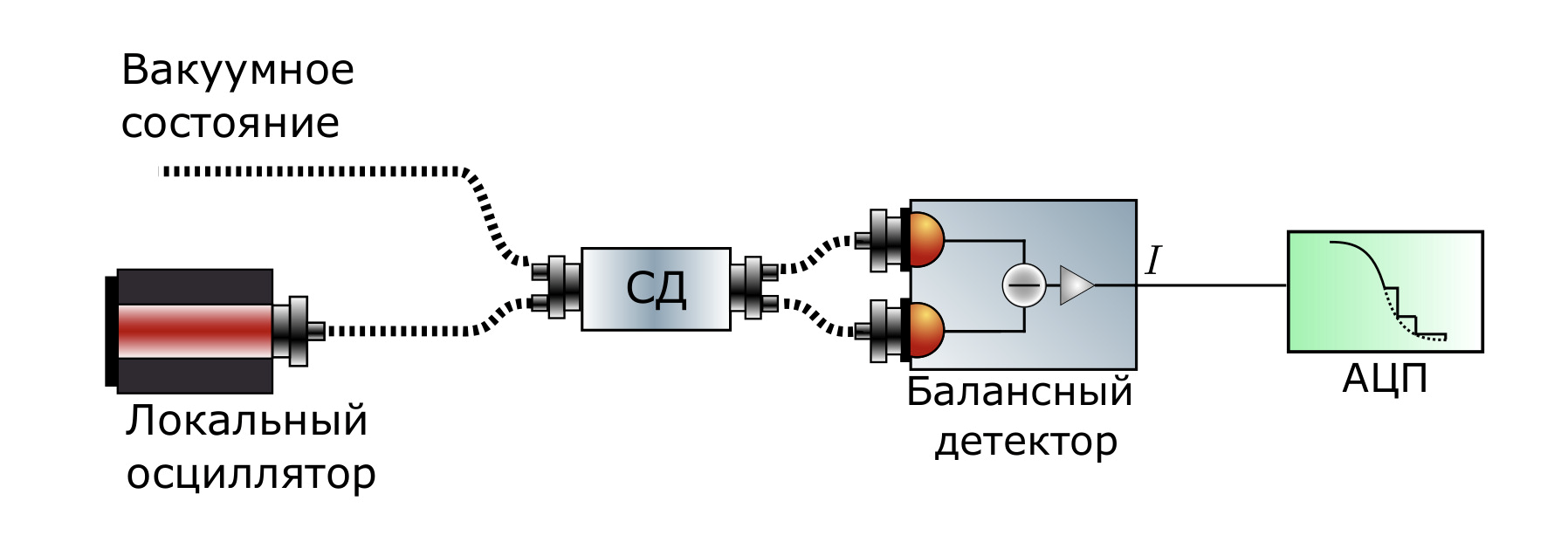
В нашей компании мы разрабатываем квантовый генератор случайных чисел, основанный на флуктуациях вакуума (Рисунок 2).

Принципом работы данного типа генераторов является извлечение случайности из квантового шума, получаемого после вычитания на балансном детекторе сигналов, полученных с выходов светоделителя (рисунок 3). На один из входов светоделителя при помощи локального осциллятора (лазера) подается когерентное состояние, а на второй — вакуум, на светоделителе (СД) эти сигналы смешиваются, а затем сигналы с его выходов поступают на балансный детектор (состоящий из фотодиодов с одинаковыми характеристиками и вычитающей схемы), где вычитаются друг из друга. Полученный при этом итоговый сигнал является квантовым шумом, который можно при помощи последующей обработки аналого-цифрового преобразователя (АЦП) превратить в случайную последовательность.
Максимальная случайность, которая может быть извлечена из последовательности, характеризуется минимальной энтропией (энтропия Реньи). Учитывая, что классическая составляющая шума может быть скомпрометирована, величина квантовой случайности характеризуется условной энтропией, которая учитывает возможность нарушителя использовать классический шум для управления генератором.
Энтропия Реньи с параметром а определяется выражением:

При a → 1 получаем случай энтропии Шеннона, при a → ∞ энтропия Реньи дает мин-энтропию, которая является наиболее консервативным способом оценки непредсказуемости:

С помощью мин-энтропии определяется количество равномерно распределенных бит, которые могут быть извлечены из конкретного распределения. При использовании такой оценки для практических устройств ГСЧ предполагается, что потенциальный нарушитель имеет максимальную вероятность угадать значение случайной величины.
Важным этапом работы любого физического генератора случайных чисел
является пост-обработка полученных экспериментально последовательностей. Блок постобработки получает на входе необработанную последовательность бит после АЦП и формирует из них более короткую последовательность, свободную от корреляций. Подобная операция называется экстракцией случайных бит. Экстракторы случайности — это функции (хэш-функции), которые преобразуют биты из необработанной последовательности в последовательность бит с сохранением части или всей случайности входной последовательности и имеющую распределение максимально близкое к равномерному. Существует большое количество экстракторов случайных бит. Компромисс выбора конкретной хэш-функции состоит в определении баланса между быстродействием и сохранением «случайности».
Одним из оптимальных экстракторов случайности является хэш-функция на основе матрицы Теплица, заключающееся в операции свертки исходной последовательности с некоторой последовательностью (ядром), состоящей из определенного конечного числа бит. Технически свертка реализуется умножением исходной последовательности на матрицу Теплица, составленную из выбранной последовательности бит. Размер матрицы определяется двумя параметрами: оценкой минимальной энтропии исходной последовательности и конечной требуемой скоростью генерации случайной последовательности бит.

Несмотря на то, что невозможно абсолютно точно оценить качество генерируемой случайной последовательности, есть методы обнаружения в ней корреляций, по которым можно отследить некорректную работу ГСЧ. Как правило, используются следующие наиболее известные батареи статистических тестов, которые применяются для оценки случайных последовательностей: DieHard и NIST. На хабре есть хорошая статья про то, как работают тесты NIST.
Таблица 1 – результаты прохождения статистических тестов NIST
|
№ |
Название теста |
Определяемый результат |
Результат |
|---|---|---|---|
|
1 |
Частотный тест |
Слишком много нулей или единиц |
Успешно |
|
2 |
Проверка кумулятивных сумм |
Слишком много нулей или единиц в начале последовательности |
Успешно |
|
3 |
Проверка «дырок» в подпоследовательностях |
Отклонение в распределении последовательностей единиц |
Успешно |
|
4 |
Проверка «дырок» |
Большое (малое) число подпоследовательностей нулей и единиц свидетельствует, что колебание потока бит слишком быстрое (медленное) |
Успешно |
|
5 |
Проверка рангов матриц |
Отклонение распределения рангов матриц от соответствующего распределения для истинно случайной последовательности, связанное с периодичностью последовательностей |
Успешно |
|
6 |
Спектральный тест |
Периодические свойства последовательности |
Успешно |
|
7 |
Проверка непересекающихся шаблонов |
Непериодические шаблоны встречаются слишком часто |
Успешно |
|
8 |
Проверка пересекающихся шаблонов |
Слишком часто встречаются m-битные последовательности единиц |
Успешно |
|
9 |
Универсальный статистический тест Маурера |
Сжимаемость (регулярность) последовательности |
Успешно |
|
10 |
Проверка случайных отклонений |
Отклонение от распределения числа появлений подпоследовательностей определённого вида |
Успешно |
|
11 |
Разновидность проверки случайных отклонений |
Отклонение от распределения числа появлений подпоследовательностей определённого вида |
Успешно |
|
12 |
Проверка аппроксимированной энтропии |
Неравномерность распределения m-битных слов. Малые значения означают высокую повторяемость |
Успешно |
|
13 |
Проверка серий |
Неравномерность распределения m-битных слов |
Успешно |
|
14 |
Сжатие при помощи алгоритма Лемпела-Зива |
Большая сжимаемость, чем истинно случайная последовательность |
Успешно |
|
15 |
Линейная сложность |
Отклонение от распределения линейной сложности для конечной длины подстроки |
Успешно |
Для разработанного ФГСЧ, включающего в качестве основных компонент (Рисунок 3):
• лазер c длиной волны 1550 нм и мощностью 5*10-3 Вт
• балансный детектор с симетричным светоделителем,
• АЦП 14 бит с частотой дискретизации 1 — 1.25 ГГц,
Мы получаем последовательность случайных чисел с минимальной энтропией 10-12 бит в зависимости от уровня шума входящих компонент. При этом, скорость генерации случайных чисел составляет порядка 500 Мбит/с. При этом батареи тестов будут успешно пройдены (Таблица 1).


