
Итак, вы программист. Зачем вам вообще могут понадобится полиномы? Например затем, что это хорошая геометрическая глина, из которой можно слепить разные вещи.
Из нашей статьи, объясняющей сущность математического анализа на примере python’а, крови и динамита, видно, что вы можете анализировать и синтезировать произвольные функции в качестве многочленов. Однако вовсе не обязательно работать именно с функциями. Иногда вам может понадобиться смоделировать сплайн из нескольких точек или свойств, вроде тангенсов кривых. Например, вам надо слепить какую-нибудь анимацию, или приятный видео эффект, или провести кривую, проходящую через определенные точки, или создать поверхность плоскую в одном месте и изогнутую в другом.
Многочлены, в том числе даже сплайновые, могут далеко не всегда оказаться лучшим инструментом для этой задачи, однако они обладают некоторыми чертами, которые программисты очень ценят. Они просты и универсальны по своей природе, а также, что особенно важно, очень эффективны с точки зрения производительности. Возьмем, например следующий полином:
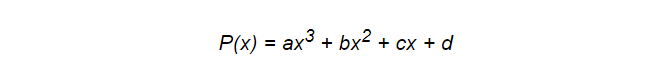
Для его вычисления требуется всего 6 действий умножения и 3 сложения. Это важно, поскольку ваша модель будет постоянно подвергаться вычислениям. Но и здесь мы можем произвести оптимизацию. В этом нам поможет схема Горнера. С ее помощью тот же самый многочлен можно записать в виде

А это уже всего 3 умножения и 3 сложения. Вот видите, мы только начали, а вы уже научились избавляться от одной трети вычислений.
Полиномиальная интерполяция
Задача адаптации многолчена n-ной степени под n+1 точку пространства называется полиномиальной интерполяцией. Существует несколько способов ее реализации. Вы можете воспользоваться интерполяционными формулами Ньютона или Лагранжа, однако самый простой способ получения интерполяционного многочлена — решение системы линейных уравнений.
Если многочлен проходит через точку, значит, мы, очевидно, можем утверждать, что P(xi) = yi. Допустим, мы хотим адаптировать полином под набор из трех точек. Это означает, что:

В общем случае, мы не можем провести прямую через три произвольные точки. И потому нам придется искривить ее, сформировав параболу. Или, иными словами, ввести многочлен второй степени, также известный как квадратичная функция.

Поскольку xs и ys известны, нам остается только решить систему и узнать коэффициенты a, b, c, и поскольку эта система из трех уравнений и трех переменных, мы как правило можем получить одно единственное решение.
Чтобы убедиться в этом попробуйте переместить положение трех точек на нижнем графике и посмотрите, что произойдет.

Этот график также очень полезен для мысленного анализа линейных систем. В общем случае, уместить прямую линию в трех точках нельзя, равно как и нельзя найти решение для системы из n уравнений при n-1 неизвестных переменных. Но иногда это возможно. Например, в случаях, когда некоторые из точек совпадают или все они намерено расположены на одной прямой.
Обратная ситуация еще интереснее. Мы можем провести бесконечное количество парабол через две заданные точки. Все они одинаково подходят в качестве решения задачи. И в то же время мы не можем получить некое однозначно лучшее решение для систем из n уравнений и n+1 переменных.
Но что если это все-таки возможно? Что если мы можем ввести некоторый дополнительный критерий для выбора наиболее подходящего варианта?
Синтез
Подобные вопросы ведут нас на территорию полиномиального синтеза. В нашем случает это нечто среднее между полиномиальными рядами и полиномиальной интерполяцией. С помощью рядов мы можем смоделировать функцию на основе ее производных в некоторой точке, а с помощью синтеза — воспользоваться как точками, так и производными (и не только ими, но об этом в другой раз).
Производная функции тесно связана с геометрическими свойствами ее графика. Первая производная определяет тангенс угла наклона касательной, а вторая — кривизну.
Допустим нам необходимо определить функцию, проходящую через две точки, зная ее тангенс в обоих точках. В таком случае мы можем легко синтезировать ее в виде многочлена.
Как и ранее, нам понадобится записать систему уравнений. Теперь нам нужны четыре условия, поэтому нам следует выбрать многочлен 3 степени, то есть кубическую функцию.
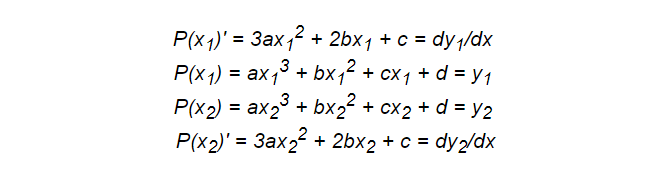
Некоторые из уравнения сформированы на основе точек, а другие — производных. Сюда также можно добавлять и интегралы для введения необходимых свойств целочисленности, что делает эту технику довольно эффективной.
Но мы продолжим рассматривать функцию, соединяющую две точки непрерывной плавной прямой с тангенциальными ограничениям в этих точках.


Феномен Рунге
У полиномиальной интерполяции есть неприятное свойство, проявляющееся в увеличении роста осцилляций на обоих концах интервала с ростом количества точек. Это явление получило название феномен Рунге. Он ограничивает возможности применения простых полиномиальных интерполяций.
Другой недостаток этого подхода — его глобальность, то есть изменение всей функции вместе с малейшим изменением положения хотя бы одной точки. В сочетании с осцилляциями получается самый что ни есть хаос.

Узлы Чебышева
Один из способов борьбы с хаосом заключается в выборе специальной сетки для интерполяции — узлов Чебышева. Это специальные значения x, которые получаются путем деления полукруга с радиусом 1 на равные фрагменты и их проецирования на ось x.
Вообще, в этом приеме кроется определенное математическое волшебство, но с прагматической точки зрения, он предназначен для минимизации феномена Рунге. И хотя он не позволяет сделать интерполяцию совершенно предсказуемой, на отрезке (-1:1) все работает стабильно.

Конечно, вы можете расширить интервал по оси X настолько, насколько нужно с помощью одномерного аффинного преобразования. Не обязательно придерживаться отрезка (-1; 1).
Но интерполяция при этом сохраняет свою повсеместность. Изменение первой точки по-прежнему влияет на работу функции возле последней, хотя и не настолько существенно.
Сплайны
Существует довольно много разновидностей сплайнов, но всех их объединяет один сценарий применения. Как только глобальная интерполяция по какой-либо причине перестает годиться для наших задач, мы можем разделить наш интервал на более малые фрагменты и определить отдельные функции для интерполяции на каждом из них.
Единственное, что нам нужно учесть, так это необходимость их соединения на концах для сохранения непрерывности. Если мы гарантируем непрерывность не только итоговой, кусочно-заданной функции, но и ее первой производной, то в таком случае тангенсы каждого ее отрезка будут совпадать, а ее график будет выглядеть плавно.
Существует определенная классификация сплайнов. Например, возьмем полиномиальный сплайн, состоящий из двух фрагментов. Если каждый его фрагмент определяется полиномом третьей степени, то он называется кубическим. Он может обладать, например, таким свойством, как непрерывность первой производной, поскольку тангенсы на стыке фрагментов совпадают. Его фрагменты имеют не равную ширину. Он не естественного происхождения, поскольку мы можем управлять производными на его концах. И конечно же это интерполяционный сплайн, поскольку он проходит точно через указанные нами точки сетки.

Заключение
Вероятность того, что вам когда-либо придется реализовывать на практике собственную интерполяцию крайне мала. Существует много готовых решений и в большинстве случаев вам надо будет просто выбрать правильный инструмент для работы. Эта область знаний не так сложна, но количество неизвестных слов и названий может оттолкнуть.
Целью этого путеводителя было предоставить вам базовое понимание идей, используемых для работы с полиномами и сплайнами. Он ни в коем случае не претендует на полноту изложения, ведь на самом деле, по каждой из небольших глав этого материала написаны целые книги. Но мы надеемся, по крайней мере, что интерактивный подход к изложению в этом материале будет полезен не только для краткого ознакомления, но, если такая потребность возникнет, поможет вам освоить и более продвинутые темы.
Источник



