Рациональные звёзды.
Для ответа на ранее заданные вопросы о рациональных числах нам снова понадобится небольшое отступление. Сначала вспомним, что в процессе деления «уголком» мы постоянно получаем остаток от деления некоторой части делимого числа на делитель. При этом целая часть деления записывается в результат, а остаток от деления домножается на основание системы счисления, после чего процедура деления с остатком повторяется до тех пор, пока не будет обнаружен период или же не сократятся все множители делителя и мы получим конечную дробь. Выглядит это так:
5 | 3 ------ 1.66(6) 3 20 18 20 18 2 ... Здесь остаток от вычитания 18 из 20 всегда равен двойке, которую потом домножаем на основание десятичной системы счисления.
Теперь подумаем, чем отличается деление 5 на 3 от, например, деления 1 на 3? Ответ простой — наличием целой части в результате. Но мы задались вопросом про период и ту часть, которая идёт перед периодом (называется — предпериод), но не входит в целую часть результата. Поэтому нам нет необходимости рассматривать целую часть. Значит в данном примере можно исключить из рассмотрения все числа, большие чем 3 или равные ему. И что ещё более интересно — закономерности деления во многом проявляются вообще без какого-либо другого числа, кроме единицы. То есть достаточно изучить деление единицы на ряд целых чисел, больших единицы, и мы с вами поймём, как ответить на все заданные вопросы, а заодно повстречаем весьма приличное количество новых звёзд.
А пока мы не приступили к серьёзному изучению предмета — немного фокусов. Вы знаете, что делить можно «наоборот»? Не так, как мы привыкли со школы, а начиная с конца. Покажем это на другом примере, в которм возьмём последний остаток и отталкиваясь от него вычислим период дроби. Вспомним, что остаток при делении 5 на 3 у нас был равен 2. Какое число мы вычитали последним, что бы получить двойку? Нам не нужно вспоминать, потому что мы знаем, что вычитаем числа всегда из домноженного на 10 предыдущего остатка, то есть последняя цифра уменьшаемого всегда равна 0. Это значит, что достаточно перебрать произведения тройки на числа от 1 до 9, =(3,6,9,12,15,18,21,24,27), что бы увидеть — среди них только одно оканчивается на 8 и в сумме с остатком 2 даёт ноль в последнем разряде уменьшаемого. Значит перед получением остатка 2 мы вычитали 18 из 20. Почему из 20? Потому что любое другое число с нулём в последнем разряде даст разность Х0-18 больше тройки или меньше нуля. Точно так же мы вычисляем и все остальные числа:
2 — известный остаток
18 — дополнение до числа с нулём, одновременно показывающее значение очередного разряда в результате — 6 (6*3=18)
20 — подходящее число с нулём
2 — число с нулём до домножения на 10 (=20/10)
18 — дополнение до числа с нулём
20 — подходящее число с нулём
…
В итоге мы получим строго ту же самую последовательность, что и при делении уголком, но «с другой стороны». Так можно вычислить «с конца» период любых периодических дробей. А что такое предпериод (и неактуальность его вычисления для данного случая показанным способом) мы увидим дальше. Целая же часть результата всегда равна нулю при использовании единицы в качестве делимого, поэтому мы опять лишены необходимости вычислять что-то ещё, кроме периода.
Теперь вспомним, как мы делим единицу на три: . Здесь всё просто, период короткий, предпериода нет, вроде бы ничего примечательного. Но давайте попробуем умножить результат деления снова на три: , то есть . А в начале было так: . Не замечаете разницу? На входе была единица, а после прямого и обратного действий, получаем… Как бы это попроще назвать? То есть если проследить всю цепочку девяток до бесконечности, то мы поймём, что перед нами единица, но всё же какая-то она не такая, вы не находите? Ну не похожа на оригинал, и всё тут. Математики скажут, что это всего лишь две формы записи одного и того же числа, но житейское понимание «одного и того же» немного восстаёт против таких определений. В принципе с математиками трудно не согласиться, ведь много девяток после запятой отличаются от единицы чем-то совсем эфемерным, бесконечно малым и в пределе стремящимся к нулю. Но вот конкретно вы можете охватить мыслью весь этот набор бесконечностей? Бесконечное количество девяток, бесконечно малое отличие, стремящееся к нулю при движении вдоль ряда девяток в бесконечность. И теперь сравним это с такой записью — 1. Один знак — и нам всё ясно. А сколько знаков было в рассуждениях про равенство бесконечного количества девяток единице? То есть разница всё же есть? Или ваш мозг легко игнорирует такие мелочи в наборе отличий? Но если мы не дойдём мысленным взором до бесконечности в списке девяток, то на том месте, на котором мы остановимся, сразу возникнет отличие, которое даже математики признают существенным — если не видеть все остальные девятки, то перед нами совсем не единица. Поэтому возникает вопрос — а можете ли вы видеть на глубину всей бесконечности? В общем — вы как хотите, а математики приказали считать данное явление одним и тем же числом. Поэтому рассмотрев и эту звезду (с прямо скажем — странным свечением), перейдём к следущей.
Из факта обнаружения бесконечного количества девяток следует занимательный вывод — если делитель единицы является простым числом, большим чем 3, то получившийся период всегда делится на 9, ну и разумеется на 3, а так же при его длине более одного знака — на 11, а при ещё большем количестве знаков — на 13, 37, 101 и так далее. И это всё независимо от делителя единицы, лишь бы он был простым и больше тройки. Можете сами проверить, например, поделите период 1/7, равный 142857 на 3, 9, 11, 13, 37.
Ну и до кучм зададимся простым вопросом — а можно ли самому сконструировать период? Да, можно. Например, мы хотим получить период 0123456789, можно найти делимое и делитель, дающие нечто подобное? Можно! Но без цифры 8. Тогда это будет 1/81. А что бы и цифра 8 появилась на своём законном месте, нам нужно будет добавить к числу 81 довольно много цифр после запятой, либо без запятой, но тогда в периоде будут присутствовать много нулей.
Ещё законономерность — для некоторых делителей единицы мы можем вообще не вычислять период, а просто сдвинуть его циклически при домножении делимого (единицы) на любое число. Например — 1/7=0.(142857), а 2/7=0.(285714), 5/7=0.(714285), 3/7=0.(428571) и так далее. Если делимое будет больше 7, то целая часть результата деления уйдёт в часть перед запятой, а период по прежнему будет состоять из тех же шести цифр, но опять циклически сдвинутых — 25/7=3.(571428), 86/7=12.(285714) и т.д. Как вам такое? Любое число при делении на 7 даёт набор одних и тех же цифр! Любое! Абсолютно любое. И да, этих «любых чисел» — бесконечное количество. А результат всегда включает 6 одних и тех же цифр. Далее вы поймёте, почему мир чисел так устроен, а пока заметим, что при делении единицы на 7 мы неявно получили абсолютно всю необходимую информацию для вычисления периода из результата денения любых других чисел на семь, ведь мы теперь знаем, что достаточно просто циклически сдвинуть один единственный результат деления. То есть ещё раз подтверждается, что нет необходимости заниматься делением любых чисел, кроме единицы, на выбранное для исследования число. Правда может возникнуть необходимость домножения на некоторые числа и запоминание промежуточных результатов, но об этом — дальше.
Теперь для получения более общего представления покажем «карту боя». Карта рисуется для деления единицы на исследуемое число, при этом деление производится во всех системах счисления с основанием меньше исследуемого числа. Карта не включает результат деления, то есть период рассматриваемой дроби, но вместо него на карте представлены остатки, получаемые на каждом этапе деления «уголком». Вот так это выглядит:
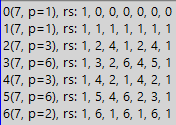
В приведённой таблице вы видите строки, от 0 и до 6. 0 — это тоже основание для системы счисления. Вы не согласны? Попробуем переубедить. Что такое система счисления? Это основание, домножаемое на некое значение, а потом складываемое с результатом, который в самом начале равен нулю. Так получаются все числа, например, в десятичной системе счисления. А если основание равно нулю? Тогда все домноженные на ноль слагаемые тоже будут равны нулю. Но что это меняет? Разве мы при этом нарушили правило построения чисел в выбранной системе счисления? Поэтому для общности картины на карте боя мы и используем все системы счисления, от 0 до 6 в случае исследования числа 7. Но помимо общности у строки с нулями будет и дополнительное предназначение.
Но что означают все эти строки? Каждая строка показывает нам последовательность остатков при делении единицы на число семь в той системе счисления, которая подписана в крайнем левом столбце. То есть при делении 1/7 в системе с основанием 0 имеем начальный остаток 1 (та единица, которую делим). Далее, как мы это всегда делали при делении уголком, домножаем первый остаток на основание системы счисления. Получаем ноль. Теперь ноль является текущим остатком. Обычно при вычислении частного после получения остатка, равного нулю, и при отсутствии в делимом числе дополнительных цифр, деление прекращают (поскольку результат получен). Но в нашем случае мы заполняем таблицу, которая не терпит пустоты, а кроме нетерпения она обладает дополнительными свойствами, которые так же требуют наличия каких-либо чисел во всех клетках. Поэтому мы продолжаем деление и делим остаток 0 на 7. Обычно, пока остаток меньше делителя, его домножают на основание системы счисления, но домножать на ноль много раз — бесполезно, поэтому просто запишем, что после домножения на ноль остаток опять стал равен нулю, и теперь занесём его в таблицу в следующую клетку. Потом повторим процедуру. И так заполним нулями все клетки в первой строке. А потом заполним вторую строку. Но она уже имеет другое основание системы счисления — единицу. После деления 1 на 7 мы имеем первый остаток — единицу. Потом домножаем на основание системы счисления, то есть на единицу. Получаем опять 1. Пишем в соотвествующую клетку. Снова домножаем на 1, снова получаем 1, снова пишем. И так до заполнения второй строки. А вот после этих двух замечательных во всех отношениях строк, мы наконец доходим до более осмысленного деления — в двоичной системе (а смысл первых двух систем станет ясен позже). Сначала у нас есть всё та же единица. Запишем единицу в третью строку. Затем умножаем на основание системы счисления (на 2). Получаем 2. 2 меньше семёрки, вычесть пока не можем, поэтому запишем остаток 2 в таблицу. Снова умножаем на 2, получаем 4, которая опять меньше 7, значит опять без изменений идёт в таблицу. А вот на следующем шаге получаем 8, которая больше 7, значит надо вычитать. Результат — 1. Пишем в таблицу. Но ранее у нас уже была единица, поэтому все остальные шаги будут теми же самыми — так мы допишем третью строку до конца. И точно так же допишем остальные строки, но не забывая, что домножать нужно уже на другое основание системы счисления.
Итак, когда мы наконец получили заполненную таблицу, можно сделать некоторые выводы. Сначала обратим внимание на повторы. Для двоичной системы имеем 1,2,4,1,2,4,1, то есть два раза по 1,2,4 и потом ещё один раз 1. Здесь список 1,2,4 соответствует периоду получившейся двоичной дроби. То есть период будет длиной 3. И хотя мы использовали остатки вместо цифр из периода, но длина от этого никак не пострадала, а потому вся информация сохранена. И даже больше — в таблице остатков информации реально больше. Но об этом чуть позже, а пока заметим, что все строки сделаны одинаковой длины для простоты изучения и из-за наличия у такого представления ряда полезных свойств. Так строки начинаются и заканчиваются единицами, что хорошо выделяет свойства числа 7. А если бы мы сокращали строки до длины периода, то не смогли бы насладиться такой красотой симметричного отображения сути числа 7.
Теперь о информации. Остатки однозначно задают цифру в соответствующей позиции периода, поэтому информация в таком представлении не теряется, но поскольку остатки могут быть больше, например, максимума одной десятичной позиции (то есть 9), то информация с их участием становится наиболее полной, ведь одна позиция в системе счисления не может рассказать нам, что остаток был, например, 19, а вот остаток 19 однозначно расскажет, какая цифра стоит в периоде и из какого предыдущего остатка мы вычитали произведение делимого (вспоминаем фокус с делением «с конца»). И к тому же мы сразу замечаем одну простую вещь — остатков не может быть больше, чем , где — исследуемое число, на которое мы делим единицу. Это очень важный момент. Кроме того можно легко доказать, что если при делении уголком повторяется ранее встречавшийся остаток, то далее будет повтор всей последовательности остатков, которая следовала ранее за повторившимся значением. Значит нам не нужно более считать, раз период найден. Если же мы записываем только цифры из периода, то повтор цифры в периоде не означает завершения вычисления. Поэтому остатки важнее цифр из периода. Но самое интересное — остатков всего , а потому периодов длиннее быть не может. Вот так вот просто мы нашли верхнюю границу количества цифр в периоде, перейдя от собственно цифр периода к остаткам. Как говорится, лёгкое движение руки и никакого мошенничества. Так проявляется польза более полной информации. Ну и поэтому ширина нашей «карты боя» для 7-ки составляет 6+1 столбец, то есть 6 столбцов под все возможные остатки и 1 столбец — для обнаружения симметрии из единиц, которая отнюдь не является обязательной для всех чисел, а потому её не стоит скрывать, экономя место под один столбец.
Ну а теперь взглянем на приведённую выше «карту» с точки зрения её полезности. Сразу можно заметить набор простых закономерностей. Каждая строка начинается с единицы, и ею же заканчивается. Вторая позиция каждой строки указывает основание системы счисления, ну а середина каждой строки содержит либо N-1, либо 1. Заметим — мы не предпринимали никаких усилий для выстраивания чисел в таблице в указанном порядке, кроме простой фиксации результатов деления в таблице. Но не смотря на игнорирование нами какого-либо порядка (кроме последовательности шагов деления), порядок сам возник из ниоткуда и нарисовал нам букву П из единиц, надел на неё кепку из нулей (с козырьком из единицы), разделил таблицу средним столбцом из единиц и её дополнения до числа 7 (по формуле 7-1=6). Кроме того, порядок сам расставил номера систем счисления во втором столбце. Сравните его с числами в самом первом слева столбце, они как раз добавлены намеренно, что бы мы точно знали, где какая система счисления. Ну а период получающихся дробей мы легко можем посчитать сами, хотя для удобства он указан в столбце со значениями вида р=Х.
На самом деле перед вами нечто вроде таблицы Менделеева, но не для химии, а для теории чисел. Точно так же, как и Менделеев, вы можете просто разглядывая таблицу обнаружить некую закономерность, а потом, точно так же, как было после Менделеева, наличие этой закономерности можно обосновать и доказать, что она повторяется для всех чисел, удовлетворяющих некому набору условий. И это — самое важно в подобных таблицах. Просто разглядывая и наблюдая закономерности можно открывать законы, например — теории чисел. Ну а для более вдумчивых читателей здесь открывается дорога к полному циклу — найдя закономерность далее нужно доказать (или опровергнуть) её актуальность для всех чисел, либо для чисел определённого класса.
Как было замечено, в данной таблице содержится полная информация о простом числе 7. Но из этой информации мы можем вывести гипотезы относительно всех простых чисел. И даже некоторые из таких гипотез уже доказаны до нас, так что нам лишь остаётся проверить чужие выводы. Доказательства давали такие известные люди, как, например, Ферма и Эйлер. Ферма дал нам такую формулу (здесь операция mod берёт остаток от деления значения слева на значение справа, в программировании она обычно обозначается значком %), то есть остаток от деления на p всегда равен единице для всех простых чисел (именно простых, это важно). Но число 7 тоже простое. А каждый остаток в каждой строке можно посчитать по такой формуле: . Здесь b — основание системы счисления (от английского base), i — номер позиции в строке (от английского index), начиная с нуля для первой позиции, N — исследуемое число (в данном случае — 7), r — остаток (от английского reminder), образующийся на i-ом шаге деления уголком и содержащийся в i-ом столбце таблицы. Сравним формулу Ферма и формулу для вычисления заданного индексом i остатка. Они идентичны для последнего члена всех последовательностей остатков. И в полном соответствии с формулой Ферма, для каждого остатка в позиции имеем равенство единице. То есть наблюдаемая невооружённым глазом закономерность в виде столбца из единиц подтверждена и доказана ещё во времена Ферма (хотя Ферма не баловал нас доказательствами, но обычно все его утверждения были верными). Эйлер добавил к формуле Ферма возможность использовать её не только для простых чисел, но и для составных чисел. Правда при этом нужно знать все делители числа, но для малых чисел это не проблема. Так во второй таблице (ниже) мы видим последовательности остатков для числа 21, которое является составным. Эйлер доказал, что остаток от деления произвольного числа в степени, равной количеству чисел, меньших и не имеющих общих делителей с N, так же равен единице. И именно этот факт мы и наблюдаем в таблице для числа 21, для которого из 20 меньших чисел 8 имеют общий с 21 делитель, а 12 — не имеют. Поэтому мы и наблюдаем в 12-м столбце (при индексации с нуля) много единиц. И единицы эти не в конце строк, потому что часть чисел, которые меньше 21, имеют с 21 общие делители. А вот для простых чисел ни одно меньшее число не имеет с ними общих делителей, поэтому количество чисел без общих делителей у простых всегда больше, чем у составных. И потому единичные остатки в таблице у простых — дальше, чем у составных. Но обратите внимание — не все значения в 12-м столбце таблицы для 21 равны единице. Неужели Эйлер ошибся? Нет, просто он не предполагал использовать свою формулу для работы с числами, которые можно сократить, и как раз в строках, которые кратны 3 и 7 (делители числа 21) мы имеем расхождение с формулой Эйлера. В целом получается, что Ферма с Эйлером дали нам годные формулы, полезные для понимания проблем делимости чисел, а приведённые таблицы во всей красе подтверждают результаты Эйлера и Ферма.

Хотя стоит заметить, что ни Ферма, ни Эйлер про приведённую таблицу не знали. А если знали, то никому о ней не рассказывали. Хотя с другой стороны — в их времена альтернативные десятичной системы счисления были несколько менее популярны, нежели в наше время. Тогда даже про десятичную систему не все знали, а считали разве что на пальцах. И потому выведенная Ферма, а затем расширенная Эйлером формула для связи основания и степени, не дают нам объяснения других закономерностей данной таблицы. Поэтому нас ждут ещё звёзды, а потом период условного открытия электронных оболочек атомов, с помощью которых химики наконец объяснили магические предсказательные свойства таблицы Менделеева. Но начнём с магии.
От звёзд к магии.
Любителям головоломок известны так называемые «магические квадраты». Это таблицы, в которых нужно расположить числа таким образом, что бы суммы по вертикалям, горизонталям и двум диагоналям были бы одинаковыми. Много людей долго и упорно ломали голову над укладыванием чисел в прокрустово ложе ограничений по суммам, и даже сумели заполнить довольно большие квадраты. Но сегодня мы познакомились с гораздо более мощной магией. Да, таблица Мендеелева для теории чисел содержит в себе на много больше ограничений, а заполнить её может даже первокласник, который научится делить «уголком». Вдумайтесь — умнейшие люди заполняли магические квадраты, но так и не нашли ни общего метода заполнения, ни продвинулись в размерах даже до жалкой сотни столбцов. А первокласник вполне справится хоть с миллиардом, лишь бы у него было в наличии достаточное время. Вот такая галактика, набитая звёздами под завязку, ждёт нас в числовых квадратах.
Начнём перечислять очевидные закономерности.
Умножение. Любой ряд таблицы можно умножить на любой другой. Результатом при этом будет ряд, номер которого вычисляется как произведение номеров умножаемых рядов, делённое с остатком на исследуемое число. То есть если мы умножим ряд 2 из таблицы для 7 на ряд 3, то получим ряд 6. А если умножим ряд ряд 4 на ряд 6, то получим 24 mod 7 = 3, то есть третий ряд. А само свойство деления по модулю (то есть с остатком) делает ненужными все системы счисления, больше изучаемого числа. Так нам не нужна система счисления с основанием 24, поскольку значения остатков в ней будут точно такими же, как и в системе с основанием 3. В какой бы системе счисления мы не вычисляли остатки от деления 1/7, мы всегда получим результат, который уже есть в таблице. Занимательно? И это лишь начало.
Симметрия. Каждый второй столбец содержит верхюю и нижнюю части, которые являются отражением друг друга. А оставшиеся столбцы содержат значения, равные дополнению до N отражённого остатка. То есть во втором столбце таблицы для числа 7 число 1 дополняет 6 до 7, 2 дополняет 5 и 3 дополняет 4. В результате рассматривавшаяся выше формула дополняется следующей системой:
, для нечётных столбцов
, для чётных столбцов
Здесь N — исследуемое число (например 7), b — основание системы счисления, i — индекс столбца, начиная с нуля, r — значение остатка в заданной b и i клетке.
По горизонтали симметрия выражается упоминавшимися ранее крайними столбцами из единиц и средним столбцом из единицы и её дополнений до N. Это работает в точности только для простых чисел, а для составных бывают отклонения. Кроме того (опять только для простых чисел, но иногда и для составных) разделительный средний столбец всегда либо начинает с единицы повтор имевшего место периода остатков, либо даёт справа ряд дополнений до N для левой половины ряда. То есть если в среднем столбце единица — далее идёт повтор левой части. Если там дополнение до N, то далее идёт та же левая часть, но после вычитания из N. Таким образом из всей таблицы (для простых чисел) можно оставить лишь верхний левый квадрат со стороной (без нулевого ряда), а все остальные значения остатков однозначно выводятся на основании информации из такого квадрата. Хотя не стоит забывать, что вообще вся таблица выводится из знания одного единственного числа — делителя, при этом делимое — константа, равная 1.
Теперь суммы. В основном для простых, но иногда и для составных соблюдаются далее показанные правила. Сумма по горизонтали (без добавленного для наглядности последнего столбца) всегда кратна исследуемому числу. Сумма по вертикали так же всегда кратна исследуемому числу. Суммы остатков в пределах периода от единицы до единицы (период может быть меньше ширины таблицы) тоже кратны либо равны исследуемому числу.
Далее делимость. Ряды остатков между единицами (периоды остатков) могут быть различной длины, но все длины рядов для простых чисел всегда делят общую длину таблицы на целое число. То есть если хотя бы один ряд между единицами не делит общую длину таблицы нацело, значит перед вами составное число (сравните таблицы для 21 и 7).
Длина и уникальность. Каждый ряд чётной длины и короче, чем ширина таблицы, состоит из двух частей — ряда остатков до середины, а за ним ряд дополнений до N для начального ряда остатков. При этом все значения в рамках периода уникальны, то есть повторяются лишь с повторением периода, но в рамках периода — не повторяются никогда.
Домножение. Если каждую клетку таблицы домножить на целое число, то получим либо циклический сдвиг остатков в случае длины периода, равной ширине таблицы, либо новый ряд в тех случаях, когда период короче чем ширина таблицы. При этом в случае коротких периодов все значения в новых рядах будут уникальными, то есть ни одного из них нет в рядах, полученных делением единицы на исследуемое число, а так же в рядах, полученных домножением на другие числа и в том исходном ряде, который мы домножали на константу. Суммарно количество уникальных периодов равно ширине таблицы, делённой на длину периода (для простых чисел). А для составных во всех возможных периодах отсутствуют «запрещённые» остатки, которые при домножении на ряды, кратные делителям исследуемого числа, дают в остатке ноль, но об этом чуть позже.
В результате домножения ряда можно получить либо циклический сдвиг периода, либо новый период. Новый период так же можно циклически сдвигать, домножая его на другие значения. Общее правило для выбора сдвига или нового периода простое — если в периоде остатков есть число, на которое домножаем, то мы получим циклический сдвиг, а если такого числа нет — мы получим новый ряд. И конечно, это напрямую относится и к периодическим дробям, точнее к их периодам (следует отличать периоды из остатков от периодов из цифр в записи дроби, хотя обычно различие ясно из контекста). Так на ранее показанном примере числа 7 мы видели, что как ни домножай результат деления на 7, всегда получим один и тот же набор цифр в периоде, но циклически сдвинутых относительно эталонного деления 1/7. В случае числа 7 мы имеем период (в десятичной системе счисления) с длиной, совпадающей с шириной таблицы, поэтому никаких других цифр в нём и не может получиться (нет более остатков в наличии), но возможны только циклические сдвиги. Но есть ещё один момент — делили мы в десятичной системе, а в таблице такой строки нет. Это значит, что для её нахождения нам нужно поделить 10 на 7 и получить остаток — 3. Именно система счисления с основанием 3 полностью повторяет поведение десятичной системы в отношении остатков, поэтому именно в третьем ряду мы видим полный период, то есть с длиной, равной ширине таблицы. А что бы по остаткам получить период в десятичном выражении, можно взять любой остаток и начать делить его уголком, тогда в результате будут все цифры периода дроби. Сдвиг же периода при домножении определяется нахождением остатка от деления множителя на N в ряду остатков. Сдвиг будет равен индексу найденного остатка, то есть нам всегда нужно циклически сдвинуть период справа налево на число разрядов, равное индексу найденного остатка.
И немного зависимостей между различными исследуемыми числами:

Здесь мы видим ряды для чисел от 2 до 39 в двоичной системе. Обратите внимание на нижний ряд. От него вверх идут столбцы из чисел 1,2,4,8,16,32. После числа 32 мы видим столбец из увеличивающихся на единицу значений (25,26,27,…). В следующем столбце значения возрастают на тройку. Потом на 6, 13, 26 и т.д. Возрастание «переключается» после достижения значения, которое больше исследуемого числа (столбец слева в скобках, перед длиной периода). Так рост на единицу переключается на рост на двойку, потом на тройку и т.д. В целом все такие столбцы начинаются с , где i — индекс столбца. Ниже значение не меняется, а выше меняется в соответствии с формулой , где j — приращение при сдвиге на ряд вверх (больше нуля). То есть пока номер ряда находится между и , приращение равно j. После пересечения границы , приращение станет равным , потом границей будет , после неё приращение будет и т.д. Точно такая же закономерность характерна для любых оснований систем счисления, то есть все строки можно заменить на ряды системы счисления 10 (а на изображении мы видим результаты для двоичной системы), или любую другую, и при этом закономерность сохранится, но с заменой 2 в формуле на другое основание системы счисления.
Выше приведён не полный список закономерностей, но любителям головоломок скорее всего уже достаточно, что бы попробовать заполнить аналогичный квадрат, например, для простых чисел 11, 13, 17. Попробуйте, но не используйте метод деления уголком или возведения в степень. Вдруг вы откроете ещё какую-то закономерность, по которой формируются такие квадраты!
Предсказания.
Владельцы хрустальных шаров имеют обыкновение предсказывать будущее, ну а мы по нашим таблицам тоже можем кое что предсказать. Вы наверное уже заметили — ровные последние столбцы из единиц бывают только у простых чисел. То есть одного взгляда на таблицу достаточно, что бы понять — простое перед нами число или нет. Это первое предсказание по нашему хрустальному шару. Второе предсказание — период дроби в системе счисления (здесь k — любое целое число, больше нуля) всегда равен 2. Период дроби в системе счисления всегда равен 1 и все значения в нём тоже равны 1. Например для исследуемого числа N=11 при k=1 имеем , то есть в десятичной системе счисления , здесь длина периода равна 2, как и предсказано выше.
Теперь предскажем дополнение к формулам Эйлера и Ферма. Сначала напомним, что каждый остаток можно вычислить, имея номер его позиции и основание системы счисления по формуле , где b — основание системы счисления, i — позиция, начиная с нуля, N — исследуемое число. Эта формула соответствует формулам Ферма и Эйлера, если в ней принять позицию равной значениям, предложенным Ферма и Эйлером. Но помимо закономерности , данной нам Ферма, закономерность среднего столбца даёт нам похожую формулу — , то есть любое число в степени из простого числа, минус один, делённого на 2, даст нам либо единицу, либо p-1, где p — простое число. Формулу можно расширить на случай, когда количество периодов от единицы до единицы в пределах всей таблицы нечётное, а длина периода чётная. Тогда , где k — любое целое число, p — простое число. Эта формула отражает закономерность повторения второй части периода чётной длины, но с вычитанием из исследуемого числа, о такой зависимости было рассказано немного выше. Для чётного количества периодов чётной длины так же можно выразить формулой зависимость остатков из правой половины периода от остатков из левой половины.
А сейчас предскажем, как найти все делители числа по такой таблице. Для этого посмотрим ещё раз на таблицу для числа 21:

Сразу видно, что очень мало рядов заканчивается единицей, это говорит о составном характере числа. Как показал Эйлер в своей формуле сравнения степени составного числа с остатком 1, показатель степени в таком случае не может быть равным составному числу минус один (то есть такому значению, которое в таблице определяет крайне правую позицию), поэтому в случае числа 21 мы видим большинство рядов без единицы в конце. Но тем не менее мы так же видим несколько рядов с единицами. Почему же для них не выполняется формула Эйлера? Обратите внимание на их период, он равен 2 либо 1. То есть, как это характерно для множества формул, формула Эйлера даёт нам одно решение из множества, и в этом наборе гарантировано присутствуют единицы именно на позициях, указываемых формулой, то есть ранее последнего места в таблице, но поскольку период короткий, то он, повторяясь много раз, иногда удачно укладывается в общую ширину таблицы и мы получаем в конце некоторых рядов единицу. Такая ситуация характерна для целого набора чисел, которые названы псевдопростыми, ведь они выдают себя за простые, выставляя в некоторых рядах единицы справа. Но это не мешает нам увидеть те ряды, в которых нет единицы в конце, а потому эта ситуация никак не влияет на принципиальную возможность определять простоту или составной характер числа по предлагаемой таблице. Хотя в реальности принципы часто встречаются с ограничениями наших возможностей, но об этом позже.
Теперь делители числа 21. У них периоды начинаются и заканчиваются не единицами, а самими делителями. Это же относится и ко всем рядам на позициях, кратных делителям. Так для делителя 3 мы видим, что в строке №3 период начинается тройкой и ею же заканчивается. То же самое для ряда №7 (не смотря на то, что длина периода там равна единице). И точно так же ведут себя все кратные тройке и семёрке номера рядов. То есть отсутствие единицы в периодах есть признак обнаружения делителя исследуемого числа, либо значения, кратного делителю. Ну а единица в самом начале таких рядов рассказывает нам о длине предпериода. Для составного числа предпериод существует только в системах счисления, кратных делителям числа. Значит если вам встретилась дробь с предпериодом, знайте — она получена после деления составного числа. Длина предпериода равна количеству остатков в начале ряда, не включенных в период остатков. При делении единицы на исследуемое число предпериод всегда будет состоять из нулей. Если же домножить результат деления на другое число (или, что эквивалентно, поделить множитель на N), то получим всё тот же период, правила описания которого даны выше, плюс ушедшая старшими разрядами в предпериод часть результата умножения множителя на период. Если умножаемое число больше N, то часть старших разрядов уйдёт в целую часть результата, а предпериод останется всё той же длины.
Заметим, что если всю таблицу для составного числа домножать на число, кратное любому делителю исследуемого числа, мы получим вырождение таблицы, когда она станет почти копией таблицы другого числа, полученного после сокращения исследуемого на его делитель. Так ниже приведена таблица для числа 21, умноженного на 3, а под ней — таблица для числа 7, умноженного на 3. Если их сравнить, то становится очевидно, что мы имеем почти копию таблицы для семёрки, но раздутую в три раза по ширине и высоте. Полной копии не получится, потому что в таблице для 21 допустимы числа, которые больше 7, а в таблице для 7 такие числа не допустимы. Но если мы учтём это обстоятельство и разделим с остатком значения в таблице для 21 на число 7, то таблицы сойдутся. Хотя на примере этой почти-копии можно убедиться, что за пределами подтаблицы для 7, внутри таблицы для 21, находятся, как и было указано ранее, полные копии, которые имеет смысл просто удалить для облегчения восприятия.


Кроме того, обратите внимание на ряды нулей с строках №7 и №14. Они наглядно говорят нам о делимости числа 21, ведь мы домножили результат деления 1/21 на 3, которая сокращается и даёт результат 1/7, ну а ряд №7 в данном случае показывает результат деления 7/7, где все остатки равны 0. Ряд №14 — результат деления 14/7, и там остатки равны нулю.
Так же напомним, что до умножения таблицы на 3 в рядах №7 и 14 стояли значения, кратные 7, что даёт при умножении на них любых значений, содержащих в качестве делителя тройку, результат, кратный 21. Но как мы помним, в такой таблице можно перемножать ряды, а это означает, что любой ряд, содержащий в себе остаток, кратный 3, будучи умноженным на ряд №7 или 14, даст в соответствующей клетке ноль. Но наличие нуля в таблице означает делимость числа на основание системы счисления, в ряду которой обнаружен ноль. Поскольку 21 делится только на 3 и 7, в рядах, не кратных 3 и 7 нулей быть не должно. Именно поэтому во всех рядах, кроме кратных 3, мы не найдём остатков, кратных 3. То есть если бы такие остатки встретились, то перемножив ряд с таким остатком на ряд №7 или 14, мы получим ряд, не совпадающий с нулевым рядом, но содержащий нули. Только ряды, кратные 3 совпадут с нулевым рядом после умножения на ряды 7 или 14. Но нулевой ряд в таблице один. Как совместить один нулевой ряд и нулевые остатки при умножении на тройку рядов 7 и 14? Очень просто — нужно запретить появление кратных 3 чисел во всех рядах, кроме кратных 3. Но это правило мы придумали только что, а закономерности таблицы остатков соблюдались всегда. То есть всегда, неким занимательным образом, природа сама убирала (и убирает) запрещённые числа из неположенных для них рядов. Вот такое у нас получилось логическое предсказание алгоритма действий природы. Или лишь нашей логики? Над этим стоит подумать.
Немного о пользе.
Для чего можно применить описанные таблицы? Например, они дают нам возможность генерировать псевдослучайные последовательности. И эти последовательности имеют ряд полезных свойств. Так в каждой последовательности остатков нет повторений. Если же нам нужны повторения (для более полного имитирования случайности), то в нашем распоряжении есть значения из периода дроби, которые могут часто повторяться. Распределение остатков из полного набора последовательностей для простых чисел всегда идеально равномерное. Значения ряда остатков автоматически удерживаются в диапазоне [1,N-1]. Для получения последовательностей у нас есть бесконечное количество простых чисел, что делает количество последовательностей неограниченным. Максимальная длина последовательности не превышает значения простого числа, что даёт простой способ предсказания этого важного параметра. Наличие же нескольких последовательностей, при периоде меньшем чем N, гарантирует нам отсутствие пересечений последовательностей при их параллельной генерации, то есть загружая все ядра процессора можно вообще не думать о блокировках, синхронизациях, проверках вхождения и тому подобном, что очень сильно повышает скорость параллельной генерации. К тому же алгоритм генерации (деление уголком) доступен школьникам младших классов, а так же крайне легко реализуется программно.
Так же можно подумать о шифровании. Предсказать последовательность остатков можно зная делитель единицы, выбранную систему счисления и какое-либо значение из ряда, шифрующего данные (ведь шифровать можно пропуская сколько-то остатков). Даже при вскрытии какими-либо методами некоторых значений из шифрующей последовательности, шифроаналитик по прежнему должен будет угадывать выбранное число и основание системы счисления. Если выбирать два параметра из простых порядка десятка-другого миллиардов (а для них, в следствии скромности размера, очень просто построить таблицу их периодов, что позволит мгновенно менять шифр хоть каждую секунду), то методом грубой силы такой шифр можно будет взломать лишь перебрав не менее чем 10^18 вариантов пар. Но если даже взломают один набор данных, то через некоторый интервал (например — для каждого сообщения своя пара) шифрующая пара поменяется и всё надо начинать сначала, что может не получиться из-за отсутствия возможности получать значение из шифрующей последовательности для каждого сообщения (или даже части сообщения, при смене ключа через сколько-то байт). Для обычного компьютера это однозначно неразрешимая задача. Хотя и здесь всё упирается в открытие достаточной для таких целей теории делимости (как и в случае распространённого асимметричного шифрования).
В следующей серии поговорим и о теории делимости, и о призах, ожидающих заинтересовавшихся читателей.
Источник


