Проектируем космическую ракету с нуля. Часть 5 — Первый закон Кеплера

Содержание

Часть 1 — Задача двух тел
Часть 2 — Полу-решение задачи двух тел
Часть 3 — Ужепочти-решение задачи двух тел
Часть 4 — Второй закон Кеплера

Привет всем читателям! Сразу приступим к продолжению без лишних разглагольствований. В прошлый раз остановились на:

Это дифференциальное уравнение второго порядка, где в качестве неизвестной функции — длина радиуса вектора, зависящего от времени. Здесь $$ как мы помним, может равняться нулю в случае прямолинейного движения вдоль радиус-вектора. Этот случай слишком прост, его даже рассматривать не будем, а кто хочет может приравнять в уравнении к нулю и дальше его решить.

Здесь попытаемся решать для $$ Первым что приходит в голову (в мою пришло, когда я впервые увидел это уравнение) то, что здесь нет $$, ну, конечно, и $$ А в таких случаях (специальных) можно проводить дальнейшую замену, которая понижает порядок уравнения до первого.

В общем случае уравнение второго порядка может быть записано в виде:

У нас же — уравнение попроще, когда:

А в таких случаях можно сделать замену, которая снизит порядок уравнения:

где $$ — новая неизвестная функция, но которая зависит не напрямую от времени, а от $$ Тогда:

Здесь продифференцировали как сложную функцию, а потом штрихом обозначили производную $$ по $$ Теперь всё готово, и можно подставить:

Уравнение первого порядка, но относительно $$ вместо времени. Причём с разделяющимися переменными:

Проинтегрировать не составляет труда:

Ну добавили пол константы, какая разница? Зато потом жить проще:

Пришло время вспомнить что такое $$:

И извлечь корень:

Уравнение опять с разделяющимися переменными, и даже интеграл вроде как берётся в элементарных функциях:

И всё бы хорошо, но проблема в том, что если мы и решим, то получим обратную зависимость, то есть времени от радиуса:

А хотелось бы наоборот:

Да еще и этот $$ — думать какую ветвь выбирать. Но это не самое страшное, нужно будет рассматривать разные случаи соотношений постоянных величин под корнем: $$
Можно, конечно, и в wolframalpha вбить и прикинуть, что будет:

Это просто страх и ужас, а найти обратную элементарную функцию можно и не мечтать. А ведь нам еще нужно и угол искать:

Слишком муторное дело. И даже умение считать интегралы от обратных функций нас не спасет скорее всего.

Кстати, можно заметить некоторое свойство для угла $$ вот из этого равенства:

$$ тоже всегда больше либо меньше нуля, либо ноль. Ведь это постоянная величина (кстати, когда ноль — тогда угол постоянен и движение вдоль радиуса вектора, еще раз убедились). А это значит, что производная угла постоянна по знаку на протяжении всего движения:

в зависимости от знака $$.

Иными словами сам угол $$ — строго монотонная функция. Кто не помнит как это, вот наглядная картинка: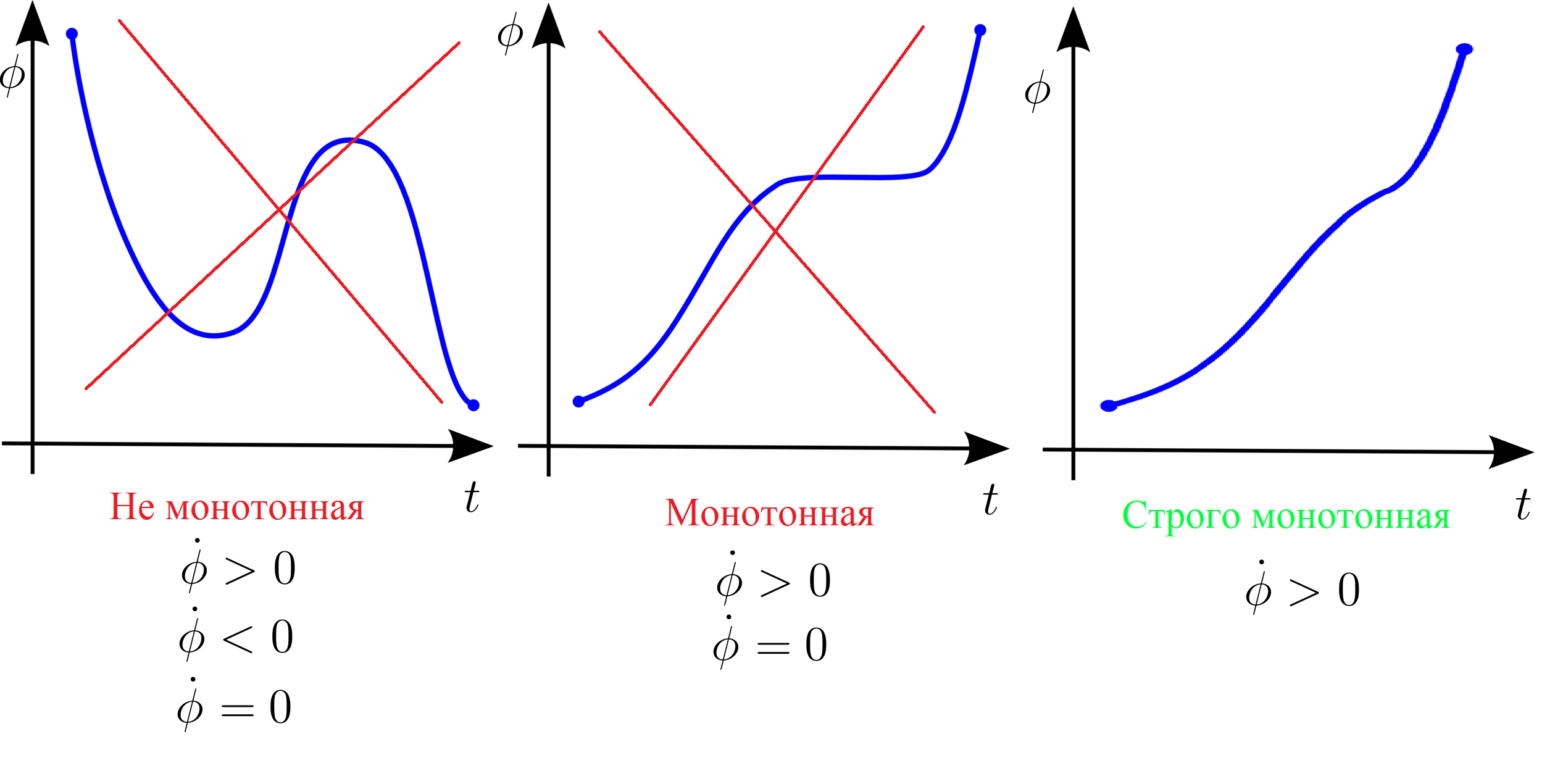

Монотонная и немонотонная функция

Этот факт подтверждает то, что мы видели при численном моделировании. Тело всегда движется в одном направлении. Никогда не останавливается (производная равна нулю) и не начинает крутиться в обратном направлении (производная изменила знак).

Соответственно траектории могут и не могут быть такими:

Синие — возможные траектории, красные — невозможные (в полярных координатах)

Ну и анимации лишними не бывают:

Производная $$ меняет знак. Таких решений у нас точно не будет.

Кстати, а эллипсы, гиперболы и параболы (сечения конуса плоскостью) — очень даже возможны. Мы это в прошлый раз видели, численно посчитав.

Я хотел сделать свой ликбез по коническим сечениям, но сегодня мне стало лень, а статью хочется уже опубликовать. Возможно сделаю когда нибудь в будущем. А пока можно ограничиться этим: шары Данделена — вот откуда у эллипсов фокусы растут.

В полярных координатах коники можно задать так (с центром в одном из фокусов и нулевым направлением вдоль главной оси):

где $$ обозначает эксцентриситет, а $$ фокальный параметр.

И о чудо, все три вида коник задаются одним уравнением, и лишь эксцентриситет определяет кем сегодня коника станет.

Эллипс ($$):

Эллипс

Парабола ($$):

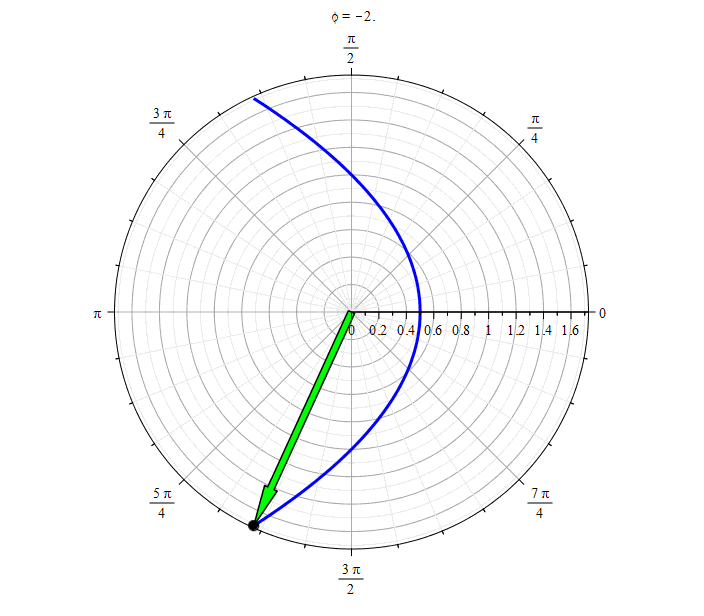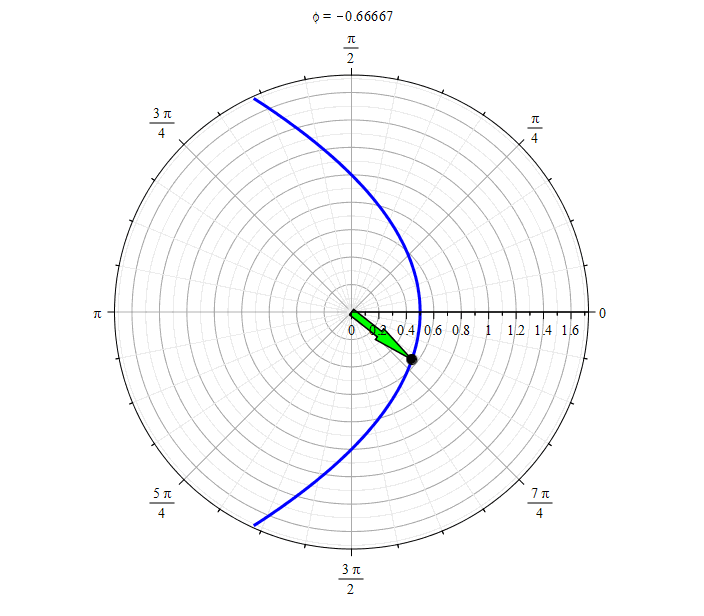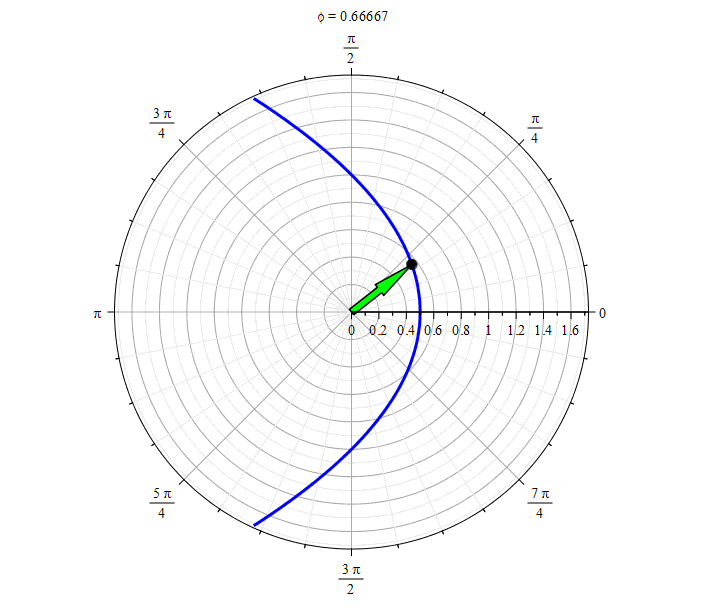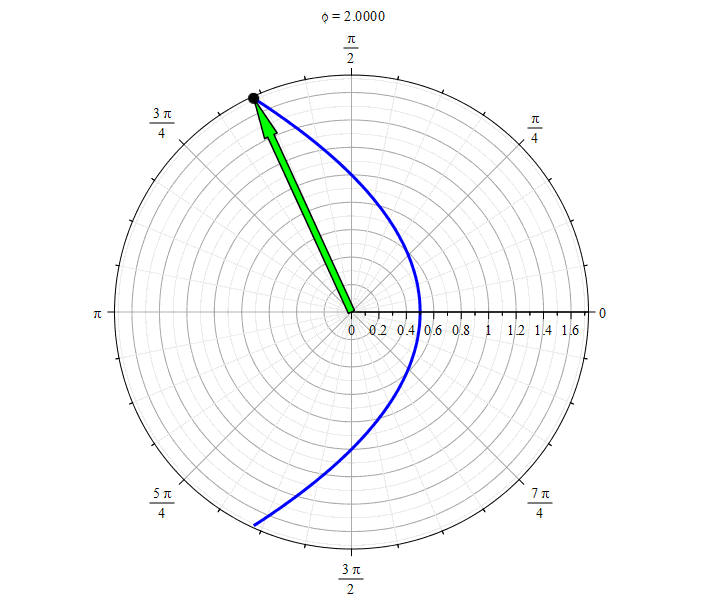
Парабола

Гипербола ($$

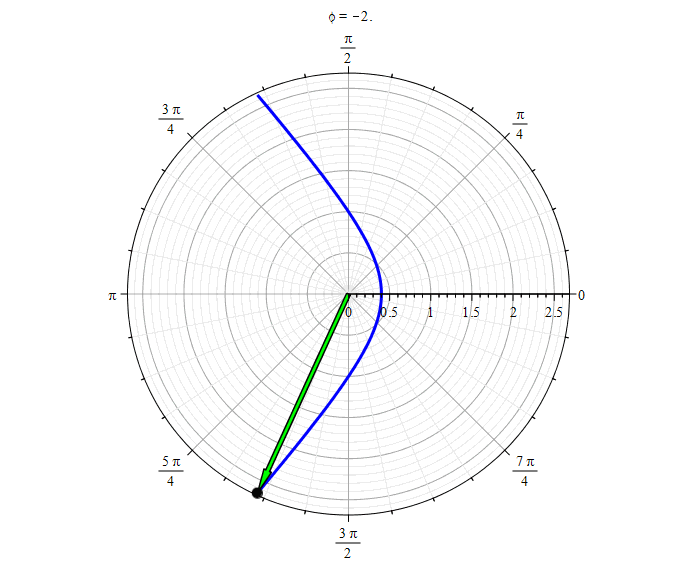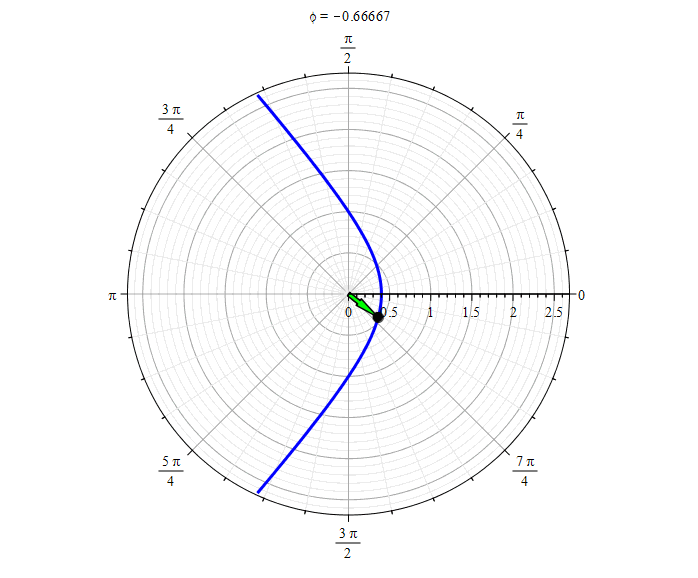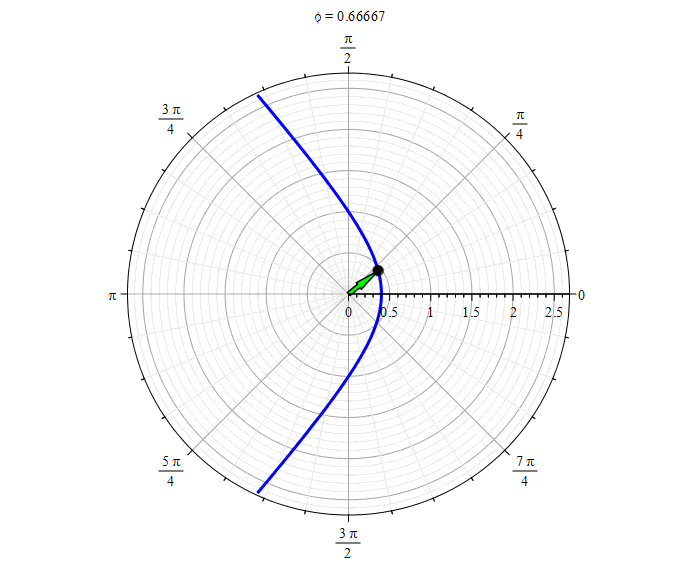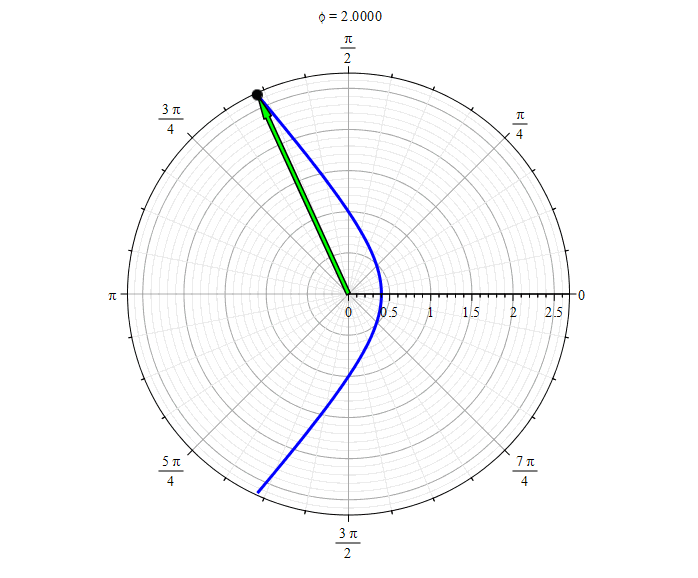
Гипербола

Очень всё похоже на траектории движения спутника, полученные численным моделированием…

Как видим, здесь $$ — радиус как функция от угла. И выражения довольно таки простые. Так может имеет смысл найти сначала зависимость радиуса от угла, а потом угла как функции времени? Можно попробовать и проверить нашу гипотезу, что решения являются кониками.

Вспомним что у нас есть:
begin{equation*}
begin{cases}
dot{phi} = dfrac{h}{rho^{2}},
\
dot{rho} = pmdfrac{sqrt{Crho^{2} + 2murho — h^{2}}}{rho}.
end{cases}
end{equation*}
Поделив одно на другое, можно избавиться от $$:

Но опять неудобно получается, наоборот:

Этот интеграл конечно можно взять и даже, скорее всего, потом найти обратную функцию труда не составит. Но есть способ попроще найти зависимость $$

Мы предполагаем, что решение будет иметь такой вид:

Вот этого уравнения:

Но производная по времени, всё же. А нам бы по углу. Ничего не мешает просто сделать сложную функцию:

и дальше продифференцировать пару раз, при этом используя уже полученные нами факты ($$).

Но перед этим само уравнение и предполагаемое решение само просится сделать такую замену:

Тогда сама функция $$ будет такой:

А это решения вот таких элементарных диффуров:

То есть сделав последовательную замену:

Можно надеяться, что уравнение будет сведено к очень простенькому.

Приступим:

Подставляя в исходное будет так:

И продолжим, пусть теперь:

Да, немножко поднапрячься нужно, чтобы всё продифференцировать и не ошибиться, но всё-таки дифференцировать это не интегрировать. Да и вообще, всё можно машине поручить, она правильно возьмет производную. Машины, конечно, могут и интегрировать, но не всегда. А вот дифференцировать всё что угодно. Интегрирование всё-таки — это творчество и всегда ним останется IMHO (Ломать — не строить).

В итоге, что у нас есть:

Ну что, будем решать это уравнение?

Это линейное дифф. уравнение второго порядка (вторая производная) неоднородное (справа не ноль). Но неоднородность слишком не усложняет нам процесс решения, так как справа константа, еще и больше нуля всегда (h не равно нулю, кто хотел тот рассмотрел этот случай еще в самом начале, и для этого не нужно было всё выше написанное проделывать).

Стандартный метод решения, но для красивости, всё запишем, ничего не пропустим:

А значит решение будет иметь вид:

Общее решение будет как сумма однородного и частного. Частное можно искать в виде константы:

Тогда общее решение:

Дифференцируя два раза и подставляя в исходное уравнение, находим константу частного решения:

Ну вот, так совпало, что константа это и есть правая часть нашего уравнения. В итоге:

Здесь у нас две произвольные константы (уравнение всё таки второго порядка), которые определяются из начальных условий. Но проблема в том, что мы предполагали найти в таком виде решение (эллипсы, гиперболы, параболы):

Так же? Ну ничего страшного, кто хорошо знаком с тригонометрией, тот легко всё запишет как пожелает (известный трюк):

где $$ — две произвольные константы, выраженные через старые $$ несложным образом. И нам вообще это неважно, ибо это константы.

Таким образом имеем решение, в более-менее ожидаемом виде:

А неизвестные постоянные находятся тоже ожидаемо, для этого нам нужно значение функции в начальной точке, а также производная:
begin{equation*}
begin{cases}
u(0) = u_{0},
\
u^{‘}(0) = u^{‘}_{0}.
end{cases}
end{equation*}
Не стоит также забывать, что зависимость здесь от угла, а не от времени:

Нужна производная, пожалуйста:

И система для нахождения произвольных констант:
begin{equation*}
begin{cases}
dfrac{mu}{h^{2}} + Acos(0 — omega) = u_{0},
\
-Asin(0 — omega) = u^{‘}_{0}.
end{cases}
end{equation*}
begin{equation*}
begin{cases}
Acos(omega) = u_{0} — dfrac{mu}{h^{2}} = a,
\
Asin(omega) = u^{‘}_{0} = b.
end{cases}
end{equation*}
Для удобства обозначили за a и b правые части. Теперь легко найти $$ возведя в квадраты равенства и сложив их:

Вероятно нужно будет выбрать +, ведь $$ — это эксцентриситет. Ну да Бог с ним, потом если что и пере-обозначить можно будет в $$.
Начальный угол $$ можно найти поделив одно уравнение на другое:

Вроде всё нашли, но теперь бы распутать клубок с $$:
begin{equation*}
begin{cases}
a = u_{0} — dfrac{mu}{h^{2}},
\
b = u^{‘}_{0}.
end{cases}
end{equation*}
Разберем и вспомним что здесь кто:

Чтобы остальное найти, нужно определиться с начальными условиями в полярной системе, они будут такие (здесь уже в начальный момент времени $$):
begin{equation*}
begin{cases}
rho(0) = rho_{0},
\
dot{rho}(0) = dot{rho}_{0},
\
phi(0) = phi_{0},
\
dot{phi}(0) = dot{phi}_{0}. \
end{cases}
end{equation*}
Тогда в любой момент времени:

В частности нулевой момент позволит определить постоянную $$:

Момент импульса в нулевой момент времени (игра слов).

И наконец:

А с производной нужно немноооожко повозиться:

То что нам нужно:

Вроде бы разобрались. Но мы то начинали не с полярной системы координат. Не с неё… Еще возни немного будет.

Как мы в полярную попали. Так:
begin{equation*}
begin{cases}
x = rhocos(phi),
\
y = rhosin(phi).
end{cases}
end{equation*}
Обратно как? Так (сразу в нулевой момент):
begin{equation*}
begin{cases}
rho_{0} = sqrt{x^{2}_{0} + y^{2}_{0}},
\
phi_{0} = arctan(dfrac{y_{0}}{x_{0}}).
end{cases}
end{equation*}
Но если кто помнит, мы в прошлые разы направили ось $$ вдоль $$, а потому должно быть так:

Соответственно:

Ну и не зря же мы до этого начальный угол брали ноль, в смысле здесь $$

Со скоростями тоже всё просто (копируем формулы с прошлой статьи):
begin{equation*}
begin{cases}
dot{x} = dot{rho}cos(phi) — rhosin(phi)dot{phi}
\
dot{y} = dot{rho}sin(phi) + rhocos(phi)dot{phi}
end{cases}
end{equation*}
Правда нужно наоборот, тут линейная система уравнений, решаем:
begin{equation*}
begin{cases}
dot{rho} = dot{x}cos(phi) + dot{y}sin(phi)
\
dot{phi} = dfrac{dot{y}cos(phi) — dot{x}sin(phi)}{rho}
end{cases}
end{equation*}
Этим можно пользоваться даже когда начальный угол не ноль, но в нашем случае:
begin{equation*}
begin{cases}
dot{rho}_{0} = dot{x}_{0}
\
dot{phi}_{0} = dfrac{dot{y}_{0}}{rho_{0}}
end{cases}
end{equation*}
Ну а дальше я не стану расписывать как из начальных данных $$ (мы ведь с этого начинали) вычислить $$. Скажу лишь что следующий шаг будет применение обратной матрицы преобразования, она где то в прошлых статьях затерялась. И таким образом мы обратно выйдем из плоскости в трехмерное пространство. Как ни уютно было в двумерном, но мы живем в трехмерном…

На сегодня всё. Продолжение следует…