После долгого полёта в глубины космоса вы с другом попадаете в плен к загадочным существам. Вам предложен выбор: остаться пленниками или победить их в игре и стать свободными. Решение принято, и вы оба садитесь за игровой стол вместе с одним из чужаков. Инопланетянин раздаёт мешочки с черными и белыми камнями. Каждый игрок, не показывая другим, достаёт из своего мешка камень задуманного цвета, а затем все трое кладут их на стол. Победителем становится тот, кто выберет камень иного цвета, чем у двух других. Черный против двух белых или наоборот. Выигравший получает монетку и кладёт на свою сторону стола. В конечном итоге победит тот, у кого окажется больше монет.
Помимо правил, в самом начале с вами поделились интересной информацией. Вероятность того, что инопланетянин достанет чёрный камень — всегда 50%. За несколько секунд до начала игры друг шепнул вам о стратегии, которой нужно придерживаться. И в результате, после бесконечного числа партий, вы оба стали победителями. Просто подфартило? Или сработала стратегия партнера?

Прелюдия
Маловероятно, что вы окажетесь в подобной ситуации. Однако игру с инопланетянами можно экстраполировать и на более реальную обстановку. Ежедневно мы сталкиваемся с необходимостью выбора. А решения принимаем как сознательно, так и на уровне инстинкта. Они могут зависеть как от чужого вмешательства, так и от событий, нам не подвластных. Как правило, мы предпочитаем поступать рационально и не полагаться на волю случая. Стремление извлечь из ситуации максимальную пользу определяет наш выбор. При этом от обстоятельств зависит и стратегия. В этой статье мы рассмотрим взаимосвязь между применяемой стратегией и последующим результатом, а также теорию игр.
Теория игр 101
Фильм «Игры разума» об известном математике Джоне Нэше, вероятно, видели все. А также слышали о многочисленных Нобелевских премиях, присуждаемых теоретикам игр. Теория игр — весьма интересная область математики, находящая применение и в реальной жизни. В ней математически моделируются стратегии взаимодействий между субъектами. Затем на основе этих моделей составляются прогнозы, что способствует более глубокому пониманию конкретного процесса. Модели могут быть либо очень сложными, либо представлять собой простой набор уравнений. Всё зависит от типа взаимодействий или количества игроков. В любом случае заглянуть краем глаза в мир теории игр будет не только интересно, но и полезно.
К коварным пришельцам мы ещё вернёмся, а пока разберём более простую игру. Подошёл вечер пятницы, и вы ломаете голову, что предложить друзьям к столу. Образовались две группы — одни хотят пиццу, другие — гамбургеры. Пицца будет доставлена за 30 минут, гамбургеры — за 15. Рассмотрим возможные сценарии:
-
Для обеих групп заказывается пицца. Но в этом случае одна из них будет недовольна.
-
Для обеих групп заказываются гамбургеры. Теперь другая смотрит косо.
-
Одной группе заказывается пицца, а другой — гамбургеры. За стол, как правило, садятся все вместе, а не челночным образом. Но тогда к прибытию пиццы гамбургеры остынут и придется их любителям есть еду холодной
Назовём одну группу — А (пицца), а другую — Б (гамбургеры). Представим эти сценарии в виде матрицы:
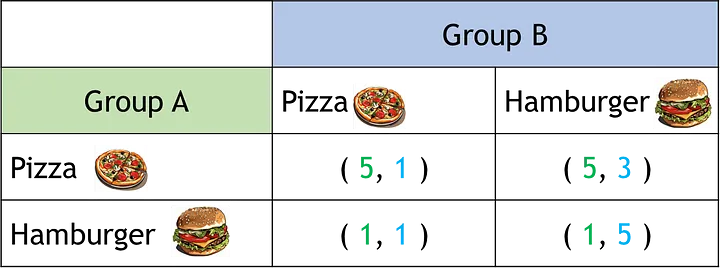
Числа в каждом сценарии называются выигрышами и представляют собой возможные варианты для каждой комбинации. Первое число — выигрыш для группы А, а второе — для группы В. Расчет выигрышей — очень важная часть аналитики в теории игр, и далеко не всегда прост. Выигрыши могут определяться несколькими составляющими. В данном случае мы задаём условное число, означающее степень удовлетворённости каждой группы. Оно является оценкой выбора гамбургеров или пиццы по пятибалльной шкале. Максимально осчастливить одновременно обе группы невозможно. Поскольку пицца будет доставлена позже, группа Б будет есть свои гамбургеры холодными. Но это же не настолько плохо, как остаться совсем без них! Такая комбинация представляет собой решение, к которому в итоге приходят обе группы. Оно получило название равновесие Нэша.
В рамках равновесия Нэша никто не может увеличить ожидаемый выигрыш, меняя собственную стратегию, в то время как другие игроки оставляют её неизменной. Предыдущий пример представляет собой такое равновесие по следующим причинам. Группа A уже достигла максимального выигрыша и не может его увеличить, в то время как группа B, отказавшись от гамбургеров, его может только уменьшить. Ещё одним классическим примером, иллюстрирующим равновесие Нэша, является знаменитая дилемма заключенного.
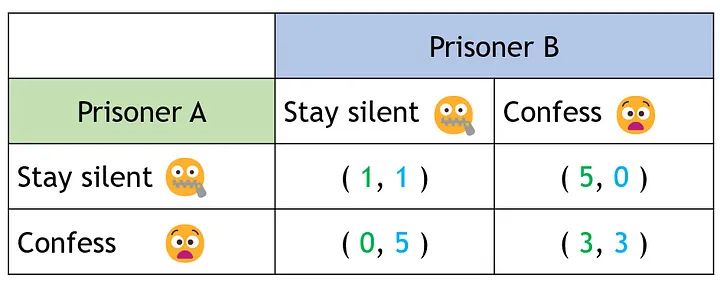
Двое заключенных допрашиваются полицией. За ними выбор – признаться в преступлении, переложив всю вину на другого, или промолчать. Выигрыш, соответствующий каждой стратегии, варьируется согласно таблице 2. В данном случае он равен количеству лет, которые им предстоит провести в тюрьме. Чем меньше число, тем значительнее выигрыш. Вот тут и возникает каверзная ситуация. Так как ни один из заключенных не знает о выборе другого, равновесие соответствует сценарию, при котором в преступлении признаются оба. На первый взгляд, исходя из таблицы выигрышей, можно сделать вывод, что хранить молчание для них, как для подельников, станет лучшей стратегией. Однако каждый из заключённых не знает, как поступит другой. Но даже при уверенности, что партнер будет молчать, лучшей стратегией с индивидуальной точки зрения всё равно будет признание. Оно может сократить тюремный срок с одного года до нуля. Таким образом у дилеммы заключенного есть только одно равновесие Нэша — стратегия, при которой оба сознаются.
Прежде чем вернуться к инопланетянам и их игре, следует отметить, что некоторые виды взаимодействий могут иметь более одного равновесия Нэша, в то время как в других случаях оно может и вовсе отсутствовать. Но это лишь тогда, когда рассматриваются чистые стратегии. Чистые стратегии предполагают наличие единственного определённого замысла. Целенаправленность в молчании или признании, в покупке пиццы либо гамбургеров. С другой стороны, смешанные стратегии в каждом плане предусматривают определенную вероятность. Можно сказать, что у заключенного есть 75% шансов промолчать и, соответственно, 25% шансов признаться. В любой конечной игре мы можем быть уверены, в наличии, по крайней мере, одного равновесия Нэша. Оно может быть в форме чистой или смешанной стратегии, либо их комбинации. Теперь, когда мы это знаем, самое время сесть за стол с инопланетянами.
Вернёмся в космос
Рисунок 1 иллюстрирует выигрыши и стратегии игры. Не трудно догадаться, что это всего лишь модифицированная версия классической игры в орлянку. Существует 8 возможных вариантов, и в двух из них никто не выигрывает, если всем трём игрокам выпадает один и тот же цвет. В остальных же случаях выигрыши очевидны. Чёрный — против двух белых, либо белый — против двух чёрных. В этой игре отсутствует чистая стратегия равновесия Нэша. Нет ни одной, которая удовлетворяла бы всех игроков. Зато в ней явно просматривается равновесие Нэша со смешанной стратегией. Для начала произведём некоторые расчёты, а затем вернёмся к исходной задаче.
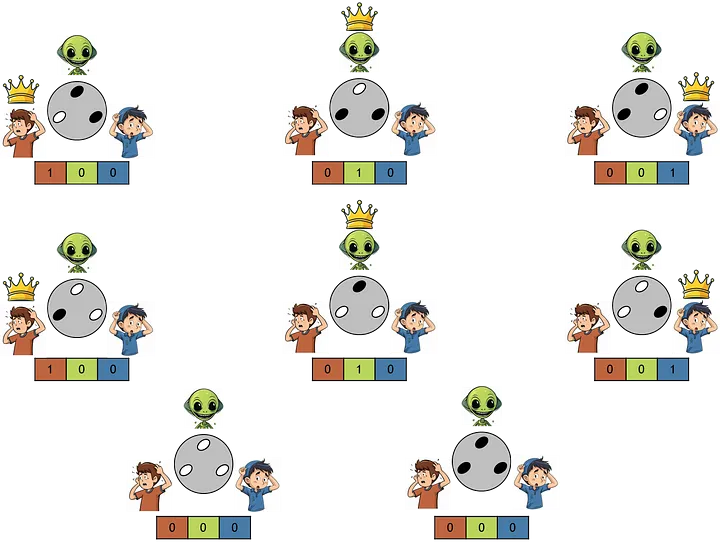
Определимся с вероятностями в каждой стратегии, а затем продолжим расчёты. Буквы на рисунке 2 обозначают вероятность игры черными или белыми для каждого игрока.

Начнём с инопланетянина. Его стратегия, при которой не имеет значения, чёрными играть или белыми, предполагает вероятности r и q. При этом игра чёрными или белыми приведёт к одинаковому результату. Это можно выразить следующим уравнением:

Применив аналогичный подход ко всем игрокам, в итоге получаем группу уравнений. В них выведены вероятности, представляющие собой равновесие Нэша при смешанной стратегии. В данном случае p=q=r=0,5. Можно взглянуть на это и по-другому. Если цвет камня для всех трёх игроков будет выпадать с вероятностью 50%, то после бесконечного числа игр их ожидает ничья. Прогнозируемое значение выигрыша для всех одинаково. Перейдя по ссылке на Jupyter Notebook, вы можете многократно моделировать эту игру, меняя вероятности для каждого участника.
В данном конкретном случае мы не заинтересованы в нахождении равновесия Нэша между тремя игроками. Напротив, нам нужна стратегия, гарантирующая победу над пришельцем. И полученная информация о нём приведёт нас к успеху. Поскольку мы знаем, что он всегда будет играть чёрными или белыми с вероятностью 50%, то один из нас может играть белыми, в то время как другой чёрными. Это и будет гарантией того, что один из нас выиграет каждую игру. После бесконечного количества попыток у инопланетянина останется ноль монет, а между нами разделятся остальные. Таблица 3 представляет собой матрицу выигрышей для двух игроков, при условии, что инопланетянин будет всегда играть черными с вероятностью 50%. Обратите внимание на то, что присутствуют два равновесия Нэша, в которых либо Том, либо Майк получают выигрыш 1, используя противоположные стратегии.
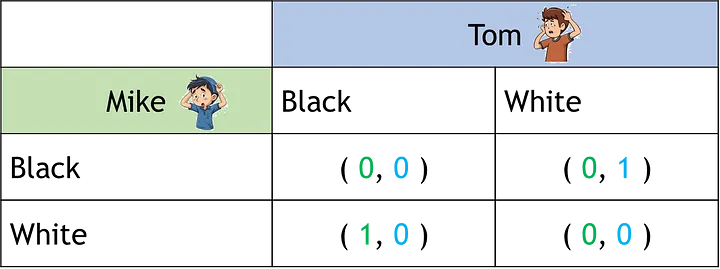
Пришелец был побеждён в его собственной игре! Сообщив, что всегда играет чёрными или белыми с вероятностью 50%, он обрёк себя на поражение. Стратегия, по которой один друг играет чёрными, а другой белыми (или наоборот) позволила выигрывать каждую партию. Однако без предварительной информации о стратегии пришельца лучшим вариантом было бы сыграть чёрными или белыми с вероятностью 50%.
Теория игр, без возможности применять её в жизненных ситуациях, не была бы настолько привлекательной. Перенесёмся из гипотетических в более реалистичные сценарии. Давайте рассмотрим другой пример.
Трюк с дополнительной гарантией
Уже долгое время вы мечтаете о покупке телевизора за 1000 долларов. Весь год откладываете деньги и в Чёрную пятницу решаете сделать себе этот подарок. При оплате кассир предлагает вам воспользоваться дополнительной гарантией на ремонтные расходы (назовём её PP) «всего за 175 долларов». Она покроет все возможные технические издержки, связанные с телевизором, в течение следующих 4 лет. Брать или не брать — вот в чём вопрос.
Для ответа на него проанализируем проблему, как игру для двух игроков. Один из них — компания, продающая телевизор, другой — покупатель. Предположим, что средняя стоимость ремонта телевизора составляет 500 долларов. Тогда матрица выигрышей будет выглядеть следующим образом:
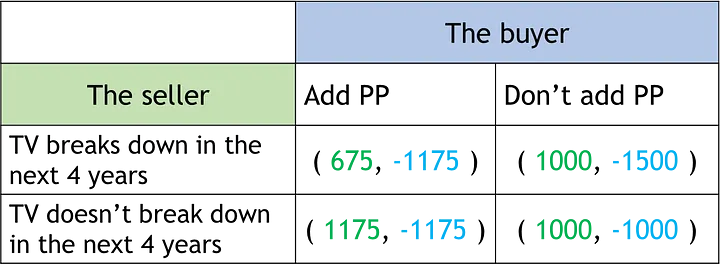
Первое число в матрице соответствует выигрышу компании, второе — выигрышу покупателя. Значения рассчитывались следующим образом.
Покупатель берёт дополнительную гарантию.
Если телевизор ломается:
-
Выигрыш (покупатель): стоимость ТВ + стоимость РР: -1000-175 = -1175
-
Выигрыш (компания): выручка от ТВ + выручка от РР — стоимость ремонта = 1000+175-500=675
Если телевизор не ломается:
-
Выигрыш (покупатель): стоимость ТВ + стоимость РР: -1000-175 = -1175
-
Выигрыш (компания): выручка от TV + выручка от PP = 1000+175 = 1175
Покупатель не берёт дополнительную гарантию.
Если телевизор ломается:
-
Выигрыш (покупатель): стоимость телевизора + стоимость ремонта: -1000-500 = -1500
-
Выигрыш (компания): выручка от TV = 1000
Если телевизор не ломается:
-
Выигрыш (покупатель): стоимость ТВ: -1000
-
Выигрыш (компания): выручка от TV = 1000
В случае, когда покупатель не берёт дополнительной гарантии (РР) и телевизор не выходит из строя, наблюдается чистая стратегия равновесия Нэша (нижний правый квадрат в Таблице 4). И это понятно, поскольку, если не оплачивать PP, лучшим сценарием окажется тот, при котором телевизор будет работать без необходимости его ремонта. Продавец же при этом заработает одну и ту же сумму независимо от того, сломается телевизор или нет.
Для понимания этого сценария важно определить чистую стратегию равновесия Нэша. Но наш первоначальный вопрос пока остаётся без ответа. Нам придётся учесть вероятность поломки телевизора в первые 4 года. Предположим, что q представляет собой эту вероятность. С её учётом ожидаемая стоимость для покупателя будет такой:

Обратите внимание на то, как мы рассчитываем ожидаемую стоимость в каждом случае покупки телевизора — с оплатой РР, и при отказе от дополнительной гарантии. В худшем случае, при абсолютной уверенности, что телевизор сломается (q=1), покупатель заплатит 1175 долларов, если возьмёт РР, и 1500 долларов, если этого не сделает. В обоих вариантах коэффициент вероятности q=0.35. Значения q показаны на рисунке 3. По нему видно, что если вероятность поломки телевизора меньше 0,35, то дополнительную гарантию лучше не оплачивать.
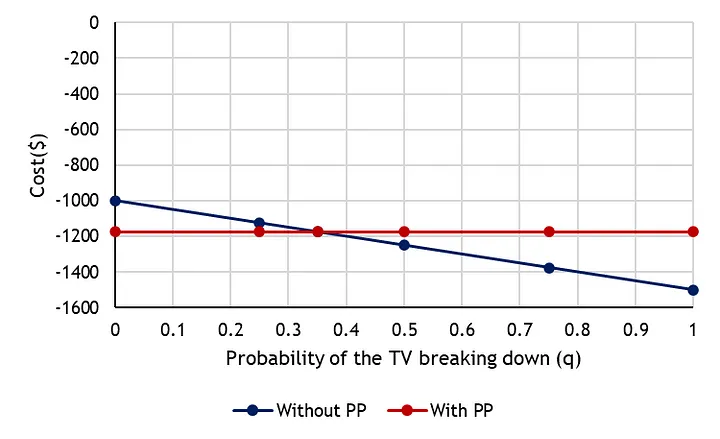
Учтите, что коэффициент 0,35 рассчитывается из значений затрат, приведённых в примере. Фактически значение q зависит только от стоимости дополнительной гарантии и стоимости ремонта.

Если ремонт телевизора обойдётся дороже, то вероятность поломки телевизора, выше которой лучше оплатить дополнительную гарантию, снижается. С другой стороны, увеличение цены самой дополнительной гарантии приведет к увеличению q. Нужно также учесть, что чем больше стоимость гарантии приближается к стоимости ремонта, тем меньше её рекомендуется покупать вне зависимости от вероятности поломки телевизора. В Jupyter Notebook вы можете рассчитать ожидаемую стоимость при изменении любой из переменных.
Эту ситуацию можно рассмотреть и с точки зрения продавца. «Зная, что вероятность поломки телевизора в первые 4 года равна Х, какой должна быть цена дополнительной гарантии, чтобы мне было безразлично, возьмут её или нет?» Можно рассчитать ожидаемые значения для обоих случаев, но на этот раз с выигрышем продавца:

Примечательно то, как правая часть уравнения соотносится с ценой телевизора. При поломке телевизора с вероятностью 0,35, ожидаемая стоимость для продавца будет одинаковой (1000 долларов) независимо от решения покупателя. Какова вероятность того, что телевизор сломается в первые 4 года? Сложный вопрос, поскольку каждый телевизор индивидуален. Однако быстрый поиск в Google выдаёт значение около 4% (0,04). Тогда стоимость дополнительной гарантии для наших значений составит 0,04 x 500 = 20 долларов. То есть, установив свою цену на неё на уровне 175 долларов, продавец получит в итоге 1155 долларов, если уговорит покупателя, и 1000 долларов, если этого не сделает! Не слабая сделка!

Таким образом, становится понятно, как продавец или компания могут использовать теорию игр для определения лучшей цены за свою услугу, чтобы в итоге остаться при максимальном выигрыше. В Jupyter вы можете поиграться и с этим примером.
Вывод
Наша жизнь наполнена решениями, которые влекут за собой совершенно разные последствия. Неважно, вымышленные это сценарии, такие как встречи с инопланетянами, или просто покупки в магазинах. Последствия эти зависят как от нас самих, так и от решений других людей. Цепочка может продолжаться бесконечно. Очень трудно контролировать действия других, но мы можем научиться подходить к каждой проблеме, как к игре. Со всеми её игроками, стратегиями и выигрышами. Для этого и предназначена теория игр, а применять её можно повсюду. Столкнувшись с трудным выбором, вспомните о ней! Возможно это поможет сэкономить вам несколько долларов или скостить несколько лет тюрьмы!


