Постпятничные клеточные автоматы: альтернативные окрестности и HROT

👾, Хабр!

В прошлой статье о циклических КА мы мельком затронули тему альтернативных окрестностей, рассмотрев несколько примеров. Несмотря на то, что ранее мы использовали только окрестности Мура и фон Неймана, существует ещё множество прочих именованных окрестностей, а потенциал для создания новых ограничен лишь нашей фантазией.

Сегодняшний обзор мы совместим с ещё одним расширением: в статье об LtL было упомянуто, что параметры рождения и выживания клетки могут поддерживать множество значений и диапазонов в некоторых прочих конфигурациях. В первую очередь речь шла, конечно, о HROT (Higher-Range Outer-Totalistic) – обобщении LtL конфигурации, на котором и будут наши сегодняшние примеры.

Тема альтернативных окрестностей крайне слабо исследована сообществом. Энтузиасты КА больше сконцентрированы на рассмотрении уже известных правил, редко отходя от общепризнанных конфигураций. И это вполне объяснимо – даже простейшая B/S конфигурация содержит огромное количество правил и паттернов, с любым отдельно взятым расширением представляя чуть ли не бесконечный потенциал для исследования. Мы же движемся как раз «в ширину», рассматривая не столько частные случаи, сколько вариативность всей области.

❯ 1. Окрестность Мура

Для порядка стоит упомянуть все именованные окрестности, и начнём со всем знакомого примера.

^{Вид окрестности на радиусах 1-4}

В нотации данная окрестность всегда обозначается как NM. Если в правиле не указано иное, принимается окрестность Мура в качестве стандартного значения.

В дальнейшем мы будем обозначать логическое правило составления окрестности на основе x и y координат, с центральной клеткой (0, 0). Для окрестности Мура же мы просто берём все значения [-R, R].

Центральная (рассматриваемая) клетка никогда не задаётся окрестностью. Принято не включать eё в подсчёт соседей, а для явного включения используется параметр M1 в правиле. Данное дополнение было введено в LtL конфигурации, и, что несколько странно, HROT обобщение этот пункт в классической нотации опускает, хотя нам, конечно, ничто не мешает использовать и его.

Каждую окрестность будем сопровождать примерами с, как минимум, одним орнаментным видом и одним случайным. Некоторые примеры подобраны специально, для соответствия окрестности, но не стоит забывать, что окрестность не является определяющим параметром для финального вида, а является только частью правила.

^{24с., 200×200, 4×100% | R2/G40/M0/S8-24/B1,3,5,7,9/NM}

:h Нотация
R – радиус поиска соседей. Регулирует окрестность.
G – количество состояний клеток. Минимум – 2 (жива/мертва), бо́льшие значения отвечают за длительность «старения» клетки, когда она уже не считается живым соседом для прочих клеток, но ещё не освободила клетку для рождения новой. Если совсем правильно, в HROT и LtL принято использовать C (Count of states).
M – булевый параметр, учитывается ли собственное состояние клетки при подсчёте соседей. В HROT данный параметр отсутствует (=всегда принимается за 0), но мы сохраним возможность использования этого параметра.
S – значения и/или диапазоны количества соседей, необходимых для выживания клетки. Диапазоны записываются через дефис (если учитывать обратную совместимость с LtL, может быть использовано двое- и троеточие или t), значения и диапазоны отделяются друг от друга запятыми.
B – полностью аналогично S, но отвечает за количество соседей, необходимых для рождения новой клетки.
N – обозначение используемой окрестности. Как раз об этом мы сегодня и говорим.
/ – разделитель между параметрами правила. В правильной нотации используются «,» (да, и между параметрами, и между диапазонами/значениями), но также встречается и вариант вовсе без разделителей между параметрами.

Характеристики примера – длительность анимации; [ускорение анимации от 100мс. на фрейм, если есть]; размер поля; размер и процент центрального заполнения на старте.

^{23с., 200×200, 100×10% | R2/G5/S2,4/B4/NM}

❯ 2. Окрестность фон Неймана

Вторая по популярности, также известная нам окрестность, строится по «Манхэттенскому расстоянию» или «метрике городских кварталов», где учитываются только смежные клетки, а диагональные достигаются за два шага.

Обозначение: NN
Правило: abs(y) + abs(x) <= R
^{38с., 200×200, 100×100% | R2/G5/S2,5-9/B3-4,10/NN}

^{30с., 200×200, 100×50% | R3/G6/S3-5/B4/NN}

Ещё немного интересных кораблей

^{30с., 200×200, 100×50% | R3/G6/S3-5/B4/NN}

^{25с., 400×400, 50×30% | R5/G8/M1/S4-6/B5/NN}

Мерцание

^{19с., 300×300, 10×100% | R3/G2/S1,3,5,7,9,11,13,15,17,19,21,23/B1,3,5,7,9,11,13,15,17,19,21,23/NN}

^{35с., 200×200, 30×100% | R1/G2/M1/S2,4/B1,3/NN}

❯ 3. Евклидово расстояние

Первая незнакомая нам окрестность немного скругляет окрестность фон Неймана всем знакомыми штанами. Для наглядности, новые, по сравнению с прошлой окрестностью, клетки отмечены синим.

Обозначение: N2
Правило: (y**2 + x**2) ** 0.5 <= R
^{21с., 200×200, 80×100% | R2/G25/S4-8/B4,6-10/N2}

^{45с., 200×200, 70×50% | R3/G4/S10-15,19/B8-15,21-28/N2}

^{25с., 200×200, 150×50% | R3/G2/S5-8,17-18,21,24,26-27/B7-8,17,19,22-28/N2}

❯ 4. Круг

Ещё большего скругления мы можем достичь, если добавим клетки, вписанные окружности которых имеют какую-либо площадь пересечения с окружностью от (0, 0) с радиусом R.

Обозначение: NC
Правило: ((y**2 + x**2) ** 0.5 <= R) | ((R**2 — 0.25 + y**2 + x**2) / (R * 2 * (y**2 + x**2)**0.5) <= 1 Надеюсь, в комментариях подскажут, как привести это правило к более простому виду. Здесь же мы, в первой части, взяли клетки, подходящие под Евклидово расстояние, и дополнили частью одной из формул () площади пересечения окружностей. Так как нам не нужно вычислять саму площадь, а достаточно удостовериться, что пересечение существует, то просто проверяем, что acos корректен.

^{25с., 550×550, 10×100% | R2/G5/S2-6/B1-2/NC}

1024×1024; G3

^{27с., 1024×1024, 10×100% | R2/G3/S2-6/B1-2/NC}

^{33с., 200×200, 100×50% | R6/G2/S37-64/B38-51/NC}

❯ 5. Шахматная доска

Пожалуй, самая недооценённая окрестность, с массой интереснейших правил.

Обозначение: NB
Правило: (y + x) % 2

^{14с., 400×400, 400×100% | R3/G2/S0-5,8,11-22,24/B6,16/NB}

^{15с., «Rivers», 200×200, 180×50% | R3/G3/S0-5,8,11-22,24/B6,16/NB}

Бонус

^{2мин., 10 запусков, 200×200, 100×50% | R10/G2/S25-28/B72-133/NB}

^{35с., 200×200, 100×50% | R2/G5/S2-3/B3,8/NB}

❯ 6. Шахматная доска: инверсия

Данная вариация куда интереснее, чем может показаться. Инверсия в данном случае вносит одно ма-а-аленькое, но очень важное изменение – рассматриваемая клетка и все её соседи по окрестности оказываются одной «чётности», чего не было в обычном шахматном виде. Это приводит к тому, что у нас на поле одновременно сосуществуют два независимых друг от друга вида, что даёт интересные результаты на некоторых правилах.

Инвертированный вид не имеет устоявшегося обозначения в нотации. Полагаю, добавление «i» – наиболее логичный вариант.

Обозначение: NBi
Правило: (y + x) % 2 == 0

^{20с., 200×200, 10×100% | R5/G13/S9-33/B16-24/NBi}

^{33с., частичное заполнение, 200×200, 150×50% | R1/G2/S1-10/B2-10/NBi}

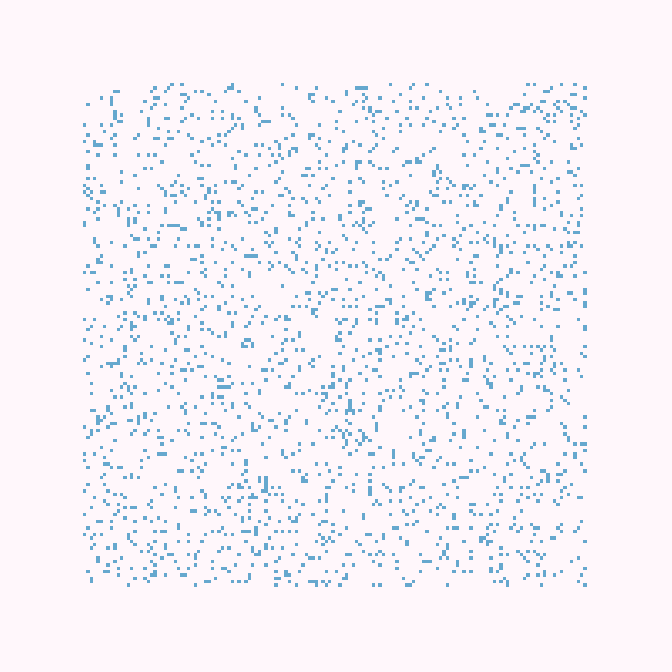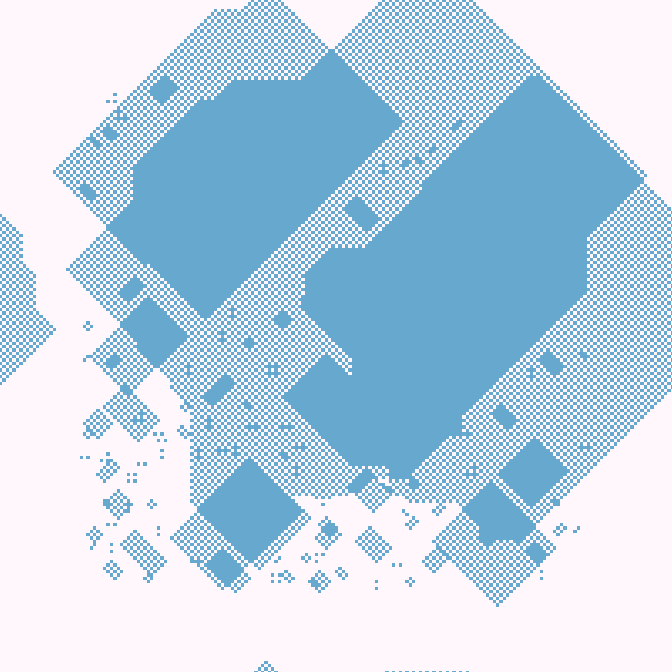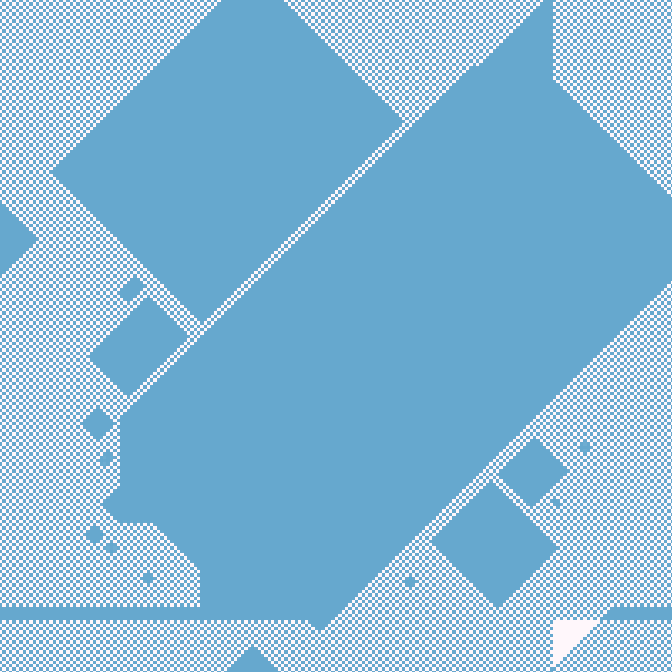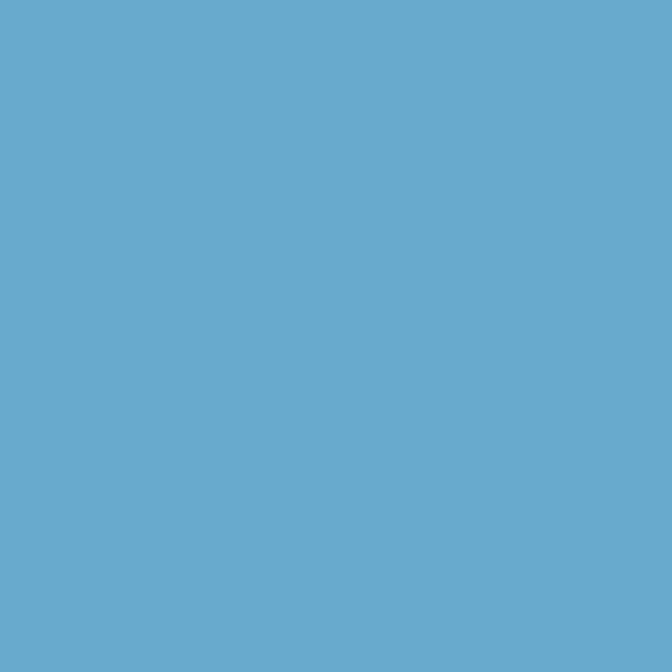
^{35с., полное заполнение, 200×200, 150×50% | R1/G2/S1-10/B2-10/NBi}

❯ 7. Решётка

Обозначение: N#
Правило: (abs(y) == 1) | (abs(x) == 1)

^{25с., 672×672, 1×100% | R2/G3/S2-4,6-9/B1/N#}

^{54с., 200×200, 100×15% | R2/G2/S4-6,12-16/B5-6,14/N#}

❯ 8. Крест

Обозначение: N+
Правило: (y == 0) | (x == 0)

^{40с., скорость ×3, 200×200, 7×100% | R4/G2/S3,6-12/B4/N+}

Спустя 10.000 итераций

^{Это финальный вид. Остались только небольшие мигалки.}

^{38с., скорость ×2, 200×200, 7×100% | R3/G2/S5-9/B3/N+}

^{24с., скорость ×1.5, 200×200, 100×70% | R3/G2/S5-9/B3/N+}

❯ 9. Андреевский крест

Ещё одна окрестность с единой «чётностью».

Названия последних двух окрестностей – прямые переводы оригинальных английских названий «cross» _{(не jebus)} и «saltire», хотя в адаптации, вероятно, ближе были бы «плюс» и «[диагональный] крест», соответственно.

Обозначение: NX
Правило: abs(y) == abs(x)

^{27с., скорость ×2, 400×400, 8×100% | R3/G2/S6-10/B3,8/NX}

Продолжение

Продолжение…

Финал

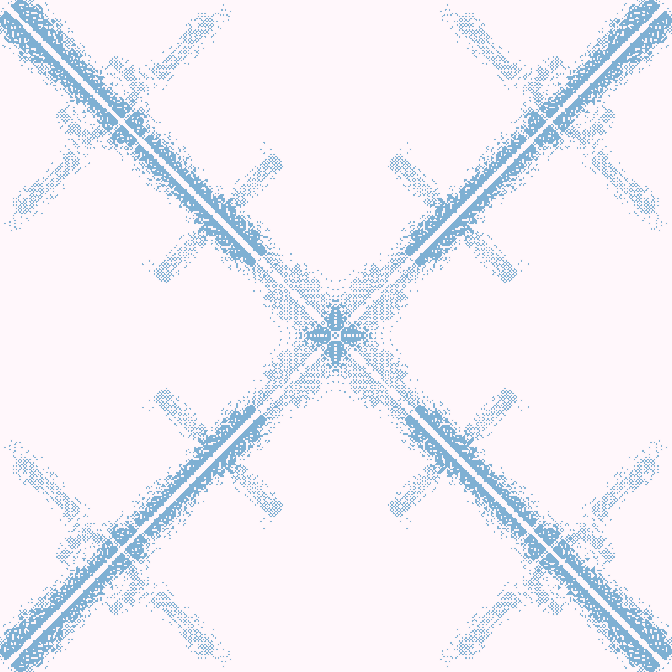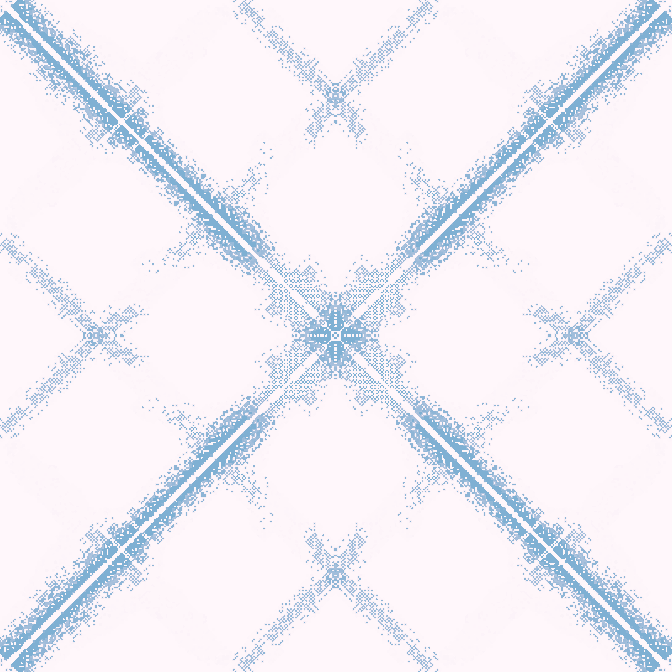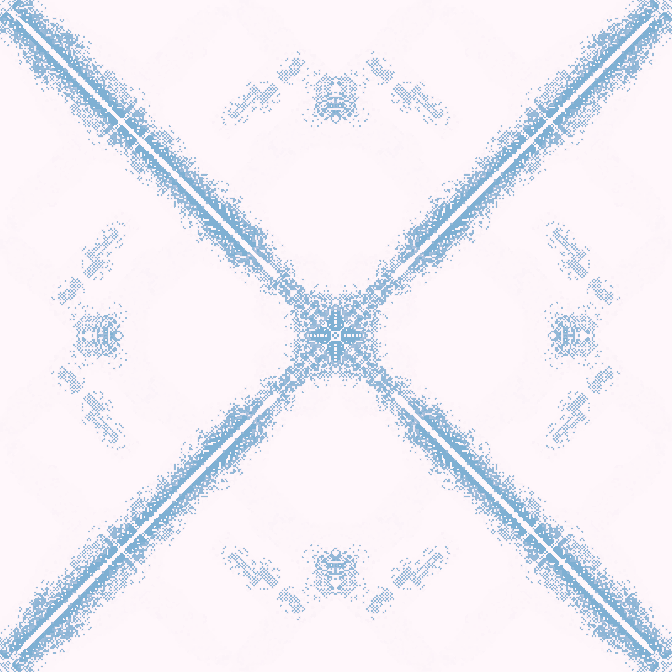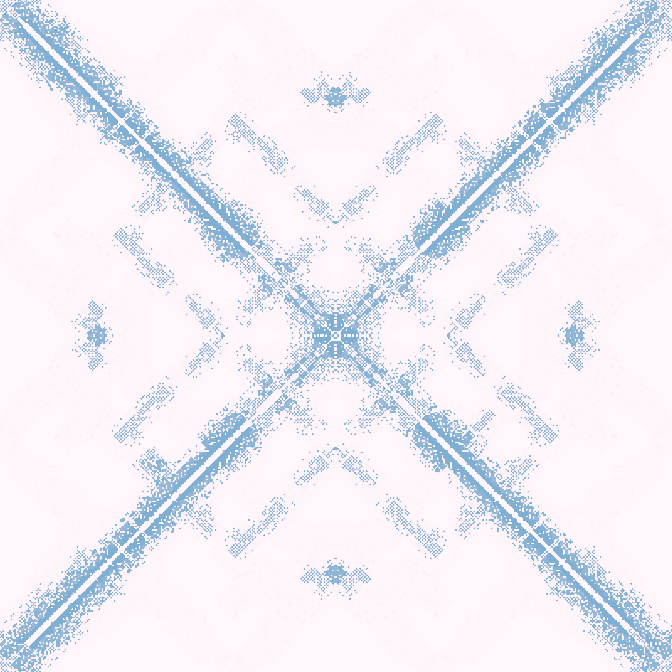
^{30с., скорость ×2, 400×400, 200×50% | R3/G2/S6-10/B3,8/NX}

❯ 10. Звезда

Объединение двух прошлых «крестов».

Обозначение: N*
Правило: (abs(y) == abs(x)) | (y == 0) | (x == 0)

^{15с., 250×250, 10×100% | R2/G12/S2-15/B1-3,6-12/N*}

^{40с., «Ледоколы», 200×200, 200×10% | R2/G3/S0-2,4-8/B6-7/N*}

---

Как упоминалось в начале, тема окрестностей довольно слабо исследована, и даже список «признанных» окрестностей с устоявшимися обозначениями заканчивается на десятом номере.

Несмотря на это, существуют ещё окрестности для прочих сеток, множество пользовательских окрестностей, а также несколько крайне занимательных частностей.

Обо всём ещё поговорим. Не переключайтесь.

Читайте также
О клеточных автоматах:

1. Базовая «life-like» конфигурация
2. Старение клеток: параметр поколений
3. Нотация Хенселя: учёт расположения соседей
4. LtL: расширенный радиус поиска соседей
5. Циклические клеточные автоматы
6. Альтернативные окрестности и HROT (вы здесь)

• Моделирование лесных пожаров: теория, клеточный автомат на Python
• Сегрегация общества: модель Шеллинга и распределение этнических групп в городах Израиля

Прочее:

• 🟢 История моделирования лесных пожаров
• 🟠 REcollapse: фаззинг с использованием unicode-нормализации
• 🔵 Хватит использовать [a-zа-яё]: правильная работа с символами и категориями Unicode в регулярных выражениях
• 🟢 Краткая история календаря и фантазии о шестидневной неделе
• 🟢 Пройти LeetCode за год: экскурсия по сайту и roadmap

← Предыдущая часть | Следующая часть (TBA) →

 

Источник