
Пьер де Ферма́, 1637

Александр Вапник, 2022
В самом начале 2016-го обилие свободного времени пробудило спавший во мне интерес к загадочным околонаучным вопросам, среди которых, конечно же, оказалась и Великая теорема Ферма. Вспомнилось, как давным-давно, году эдак в 1992-ом, школьный учитель – аккуратная пожилая женщина с мягким голосом, рассказывая о связи сторон в прямоугольном треугольнике, не прошла мимо загадочной теоремы:
– Всемирную известность получит тот, кто сможет её доказать… – размеренно завершила она, с мечтательно-печальными нотками в голосе. Быть может, она провела не одну ночь в тщетных поисках ниточки к распутыванию загадочного трёхвекового клубка. Тогдашнее впечатление от её рассказа хранилось в голове многие годы, но не более того.
Упоминаний по данной теме на просторах интернет – великое множество, однако, несмотря на обилие ферматистов в недавнем прошлом, доходчивые и конкретные примеры доказательств упорно не встречались. Месяц самостоятельных изысканий привёл меня к парадоксу, намекавшему на криволинейные поверхности, в чём я не был силён, мягко говоря. Помимо того, нашлась ещё более занимательная и, теперь уже, практически полезная задачка, заставившая почти на пять лет залипнуть в поисках её эффективного решения. Мой «ферматизм» надолго канул в лету, но вдруг, на фоне иных творческих успехов, одним нескучным вечером снова вернулся – 11-го Февраля 2022-го.

— Оно и у Ферма было, ведь юристы не бросают слов на ветер…
Итак, теорема утверждает, что не существует таких целых чисел a,b,c в натуральной степени n больше двух, которые приведут к равенству левой и правой части
Примечание
Из теоремы о представлении числа в виде разности двух квадратов заключим, что правая часть равенства состоит из множителя меньше a и множителя больше a.

Начиная со второго порядка, c – b меньше a (так же c – a меньше b). Аксиому легко проверить, представив, что в равенстве, например
500 = 1000 – 500 все числа – кубы. Тогда их первые степени (приближённо)
7,9 > 10,0 – 7,9. Это остаётся справедливым при любой комбинации значений. С увеличением порядка данное отличие будет только расти.
Таким образом, равенство может выполняться только при большем множителе, равном c + b
Получили свидетельство тому, что больший множитель альтернативного разложения квадрата (перед примечанием) может существовать только при заключительном условии.
Эквивалентный более длинный путь
Противоречие
Одновременно a = c и a = b.
Равенство верно при a,b,c = 1, но тогда неверно исходное: 1 + 1 = 1
Отметим, что тот самый больший множитель не подвергался преобразованиям, а значит, при разложении разности более высоких порядков нет необходимости приводить его в явном виде. То есть, общий случай теоремы доказывается аналогичным образом.
ПОЛУЧЕНО ОБЯЗАТЕЛЬНОЕ УСЛОВИЕ. ТЕОРЕМА ДОКАЗАНА.
ЭПИТАФИЯ
Нет сомнений, что великолепный Месьё де ФеГрма воздержался поместить на полях Арифметики Диофанта именно такую выкладку. Более того, формулировка теоремы следует, как раз, из выведенного условия. Иначе откуда мог произойти домысел об отсутствии решений в любых других степенях?
Нет сомнений, также, что многие пытливые умы за эти годы вплотную подходили к этой простой интерпретации, но кто-то не рассмотрел находку, а кто-то не рассказал о ней.
После пяти лет безуспешных изысканий над «RSA factoring challenge», где различные достижения Пьера Ферма играют весомую роль, непостижимая теорема оказалась сущим пустяком. Адаптировать под отрицательные числа – лень 😉
Суть обоснования в «Примечании», может быть не сразу ясная, берёт своё начало в основной теореме арифметики (об уникальности набора множителей составного числа) и сводится к тому, что если один из множителей является разностью x–y, то другой обязательно будет x+y (приведу на днях доказательство получше, чем в вики). Для лучшего понимания предмета стоит изучить «разность степеней» и поиграть с разложением составных чисел, например 144, как в примечании, а лучше – нечётных, чтобы разобраться в том, как множители числа соотносятся с его квадратным корнем. В Теории Чисел это называют методом Ферма, а я называю естественным методом факторизации.
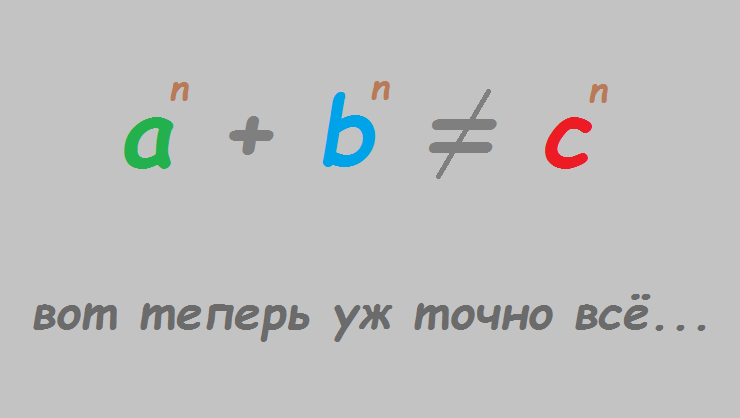
Рукожописи 🙂
P.S. Намалёванные здесь нейронные сети никак не связаны с доказательством – просто уже были на листе.


