На самом деле, эллиптические кривые — супер простая штука. Алгоритм цифровой подписи, который основан на их свойствах (ECDSA) — ещё более простая штука. ECDSA является ключевым элементом практически всех блокчейнов (включая Bitcoin, Ethereum, …). Но несмотря на то, что это очень простая штука, крайне сложно найти годное объяснение в интернете, и собрать все кусочки пазла вместе. В данной статье мы это сделаем. Вы даже не поверите, насколько всё просто!
Мы пробежимся абсолютно по всем концепциям, необходимым чтобы понять и реализовать данный алгоритм с нуля. В конце этой статьи будет полностью рабочая реализация, использующая только концепции и формулы, рассмотренные в самой статье. Без внешних зависимостей.
Мы сможем получить публичный ключ из приватного ключа, подписать сообщение приватным ключом, и проверить, что подпись корректна, используя публичный ключ. И займёт это всего лишь 100 строк кода. Кроме того, в конце будет демо в CodeSandbox, с которым можно будет поиграться.
В первую очередь статья нацелена на разработчиков, как и я сам, желающих наконец-то полностью понять, как устроена криптография на эллиптических кривых, и демистифицировать эти непонятные сочетания слов: эллиптические кривые, алгоритм цифровой подписи на эллиптических кривых, ECDSA, secp256k1, … Но статья будет полезна также и всем остальным. Она не потребует ничего большего, чем знание школьной математики.
Я рекомендую читать её часть за частью. Также я рекомендую взять листок бумаги и карандаш, и повторить все шаги, описанные в ней. Так будет ещё круче! Если вы программист — я также рекомендую написать код самостоятельно. Если нет, ничего страшного!
Статья состоит из 6 частей. Каждая часть использует концепции предыдущих (исключение: Часть II):
-
Часть I: Что нужно знать об эллиптических кривых
-
Часть II: Что нужно знать о конечных полях
-
Часть III: Эллиптические кривые на конечных полях
-
Часть IV: Практическое применение: алгоритм цифровой подписи
-
Часть V: Реализация
-
Часть VI: Live Demo
Начинаем!
Часть I. Что нужно знать об эллиптических кривых
Скорее всего, мы все так или иначе знакомы с графиками на координатных плоскостях, где переменная y каким-то образом зависит от переменной x. Например, y = x , y = x², и так далее. Скорее всего, мы все имели какой-то опыт с ними. Вот они:

Уравнение эллиптической кривой не сильно отличается!
Оно имеет форму y² = x³ + ax + b. Что такое a и b? Любые произвольные константы. Например, в эллптической кривой биткойна используются a = 0, b = 7:

Эллиптические кривые имеют 3 супер важных свойства, на которых всё работает:
На этом этапе всё может выглядеть как какая-то бессмыслица. Будет сложно ответить на вопрос “почему?”. Но прошу довериться мне ненадолго, и вы увидите, что это работает!
-
Эллиптические кривые симметричны относительно оси x.
Это означает, что для каждой точки A, лежащей на эллиптической кривой, мы можем получить её отражение, которое мы назовём -A:
-
Любая прямая линия (кроме вертикальной) пересекает эллиптическую кривую ровно в 3 точках.
Если провести прямую линию через любые две точки A и B, лежащие на кривой, мы всегда получим пересечение в третей точке. Исключение: вертикальная линия.Мы назовём третью точку —C. В соответствии с предыдущим свойством, нам нужно её отразить, чтобы получить C:

Ещё один пример:

Мы назовём точку C суммой A и B. Таким образом, C = A + B
-
Касательная к любой точке A на кривой, пересекает кривую ровно в ещё одной точке.
Мы назовём эту точку -2A. Мы уже знаем, как получить 2A:
Легче всего представлять, что касательная к точке A на самом деле пересекает точку A дважды на бесконечно малом расстоянии. Таким образом всё выглядит очень логично: прямая пересекает точки A, A и -2A, как в предыдущем свойстве.
Готово! Мы определили 3 свойства эллиптических кривых, на которых всё строится: умножение точки на -1, сложение двух разных точек, умножение точки на 2.
Пока что ничего не понятно, но здесь всё начинает работать!
У нас есть вот такая картина с точками A, 2A, -2A:

Начертим прямую линию между точками A и 2A. То, что мы получим (в соответствии с правилами выше): -3A. А дальше мы просто отразим -3A, чтобы получить 3A:

Я уверен, что всё ещё не понятно, зачем мы всё это делаем. Просто посмотрите на ещё один шаг. Что, если мы начертим прямую линию между 3A и -2A?

Видите магию? Мы получили точку -A, которая является отражением нашей точки A, с которой мы начинали. 3A + (-2A) = A.
Всё это — “алгебра” эллиптических кривых.
Просто постарайтесь осознать мощь этих трёх операций: фактически, сейчас мы можем оперировать точками на эллиптической кривой так, будто они не точки, а просто числа!
Что мы можем делать с точками на эллиптической кривой:
-
Сложение двух точек A+B
-
Вычитание двух точек. A-B, что по своей сути A + (-B)
-
Сложение двух одинаковых точек (умножение на два): A+A = 2A
-
Умножение на любое целое число (комбинируя предыдущие операции вместе, мы можем легко получить любое целое число * точку).
Что мы не можем делать с точками на эллиптической кривой:
-
Умножение двух точек друг на друга
-
Деление точки на точку
-
Деление точки на число
Посмотрим, как умножить точку на любое целое число.
Например, чтобы получить 10A:
2A = A + A
4A = 2A + 2A
8A = 4A + 4A
10A = 8A + 2A
Хорошо также заметить, что мы можем вычислить любое число * точку за логарифмическое количество операций. Примерное количество операций чтобы вычислить n * точку = log2(n)
В итоге мы можем умножить любое целое число на точку, но не существует способа получить число назад! Именно поэтому эллиптические кривые хороши для криптографии!
Небольшое неудобство на данный момент: необходимость чертить графики. Конечно же, существуют формулы для вычисления -1 * точку, для сложения точек, и для умножения точки на 2:
-
Умножение точки A на -1.
Если у нас есть точка A(x, y), мы можем легко вычислить -A путём умножения её координаты y на -1. -A(x, -y).
Примеры:
1) -1 * A(2, 2) → -A(2, -2)
2) -1 * A(1, -1) → -A(1, 1)
3) -1 * A(5, 8) → -A(5, -8)
4) -1 * A(5, -8) → -A(5, 8) -
Сложение точек A + B.
Мы можем легко сложить две точки при одном условии: они не должны лежать на вертикальной линии. То есть их координаты x не должны быть одинаковыми. Вот формула для сложения двух точек A + B = C:

-
Сложение двух одинаковых точек (умножение точки A на 2).
Операция очень похожа на предыдущую:

Готово! Время практики:
Попробуем сложить точки A(3.096, 6.055) и B(-1.650, 1.581) с данного графика:

Используем точность в 3 знака после запятой. В соответствии с формулой для сложения двух разных точек (пункт 2 выше):

Теперь найдем точку C графически:

Это работает! Да, с небольшой неточностью из-за округления, но это работает! Можете попробовать сами!
Это было всё, что нам нужно знать про эллиптические кривые и операции над ними!
Всё отлично, но пока что для построения криптографической системы не хватает пары важных свойств.
Часть II. Что нужно знать о конечных полях
Понятное дело, мы не собираемся полностью изучать теорию конечных полей. Всё, что нам нужно — это знать несколько важных свойств, и научиться работать со своего рода “алгеброй” конечных полей, чтобы двигаться дальше.
Если очень упростить, то конечные поля — это когда у нас есть конечное число элементов, которые можно складывать, умножать, делить, и алгебра продолжит работать должным образом. То есть предсказуемо, воспроизводимо и логично.
Скорее всего, вы знакомы с операцией деления с остатком. В языках программирования она выполняется оператором % (или mod). Вот как она работает:
2 mod 11 = 2
10 mod 11 = 10
11 mod 11 = 0
13 mod 11 = 2
25 mod 11 = 3Например, если посчитать числа от 0 до 33 mod 11, вот что получится: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0
Числа повторяются по кругу как на часах.
Мы назовём это конечным полем порядка 11.Нам нужно знать всего 4 важных свойства:
-
Порядок умножения не имеет значения.
a * b * c mod n это то же самое, что и (a mod n) * (b mod n) * (c mod n) mod n, что то же самое, что и (a * b mod n) * c mod n или a * (b * c mod n) mod n
Пример:
6 * 7 * 8 mod 11 = 336 mod 11 = 6, то же самое, что и:
(6 * 7 mod 11) * 8 mod 11 = (42 mod 11) * 9 mod 11 = 9 * 8 mod 11 = 72 mod 11 = 6 -
Отрицательное число mod n это то же самое, что и
n — (|отрицательное число| mod n)Примеры:
1) -4 mod 11 = 11 — (4 mod 11) = 11–4 = 7
2) -7 mod 11 = 11 — (7 mod 11) = 11–7 = 4
3) -9 mod 11 = 11 — (9 mod 11) = 11–9 = 2
4) 2 mod 11 = 11 — (2 mod 11) = 11–2 = 9
5) -13 mod 11 = 11 — (13 mod 11) = 11–2 = 9 -
“Обратное число”: для любого числа a есть такое целое число b-1, что a * b mod n = 1.
Если a * b mod 11 = 1, b называется обратным числом к a по модулю n, и наоборот: a называется обратным числом к b по модулю n.
Примеры:
1) 5 * x mod 11 = 1. Если мы попробуем подобрать x одним за другим, мы найдем x = 9. Таким образом, 9 — обратное число к 5 по модулю 11. Почему? 5 * 9 = 45, 45 mod 11 = 1.
2) 7 * x mod 11 = 1. Попробуем снова подобрать x перебором и найдем x = 8.
8 — обратное число к 7 по модулю 11. (7*8 = 56, 56 mod 11 = 1)
3) 10 * x mod 11 = 1. x = 10. Таким образом, 10 — обратное число к 10 по модулю 11. (10 * 10 = 100, 100 mod 11 = 1)Обычно обратное число находится с помощью расширенного алгоритма Евклида. Но т.к. это тема для отдельной статьи, пока что мы будем использовать грубый перебор.
Также, обратное число можно найти только когда n — простое число.
-
Деление — это то же самое, что умножение на обратное число.

Так что, когда нам нужно поделить числа по модулю, мы можем запросто сделать это. Посмотрим на пример:

Важный момент: т.к. обратное число существует только когда n — простое число, деление существует тоже только когда n — простое число.
Готово! Теперь мы знаем, как работать с “алгеброй” конечного поля порядка n!
Часть III. Эллиптические кривые на конечных полях
На этом этапе всё начинает выглядеть чуть менее очевидным и становится чуть сложнее для понимания. Но! Это — ровно то, как эллиптические кривые используются в криптографии! Нужно сделать ровно то, что сказано в названии: поместить эллиптическую кривую на конечное поле.
Вот так поменяется формула:

Всё ровно так же, как в “оригинальной” эллиптической кривой, но теперь обе части уравнения под модулем p.
Будем использовать эллиптическую кривую с таким “конфигом”:
-
a = 0
-
b = 7
-
p = 11
Найдём все существующие точки на данной кривой с помощью кода:
const a = 0; const b = 7; const p = 11; for (let x = 0; x <= p; x ++) { for (let y = 0; y <= p; y ++) { if (y**2 % p === (x**3 + a * x + b) % p) { console.log(`(${x}, ${y})`); } } }Это JavaScript, так что его можно выполнить даже в браузере. Но не обязательно.
Вот результат: (2, 2), (2, 9), (3, 1), (3, 10), (4, 4), (4, 7), (5, 0), (5,11), (6, 5), (6, 6), (7, 3), (7, 8)
Отобразим на координатной плоскости:

Теперь попробуем a=0, b=7, p=23:

Выглядит как что-то бессмысленное, правда? Никакой знакомой формы!
Но! Оказывается, что на данной эллиптической кривой сохраняются все свойства и формулы “оригинальной” эллиптической кривой!
Так что сейчас у нас есть эллиптическая кривая, которая не выглядит как эллиптическая кривая. Но! Теперь у неё конечный набор точек, и, что самое главное, она работает как эллиптическая кривая!
Только нужно только немного привести формулы в соответствие с mod p:
-
Умножение точки A на -1:
Если у нас есть точка A(x, y), мы можем легко вычислить -A путём умножения её координаты y на -1 mod p. -A(x, -y mod p).
Примеры:
1) -1 * A(2, 2) → -A(2, -2 mod 11) = -A(2, 9)
2) -1 * A(2, 9) → -A(2, -9 mod 11) = -A(2, 2)
3) -1 * A(6, 5) → -A(6, -5 mod 11) = -A(6, 6)
4) -1 * A(6, 6) → -A(6, -6 mod 11) = -A(6, 5)Как вычислить модуль отрицательного числа, смотрите в пункте 2 предыдущей части.
-
Сложение двух точек A + B:

-
Сложение двух одинаковых точек (умножение точки A на 2):

Готово! Пора попробовать в деле!
Для всех примеров ниже мы будем использовать эллиптическую кривую со следующим “конфигом”: a=0, b=7, и порядок p=11.
Выберем точку C(7, 8) и посчитаем 2C:

Дальше мы можем легко посчитать 4C:

Попробуем посчитать 4C - C, что по своей сути 4C + (-C) = 3C. Поэтому сначала вычислим -C, затем сложим 4C и -C:

А теперь попробуем сложить C + 2C, должна получиться та же точка 3C:

Алгебра эллиптических кривых на конечных полях идеально работает!
-
Одно ОЧЕНЬ важное свойство: у точек на кривой есть свой порядок n!
Это работает как модуль. Tсли порядок n точки C = 12, это означает, что 12 * C = 0 (точка не существует), 13*C = C, 16*C = 4C, 27*C = 3C. Порядок предопределен для точки. На него нельзя повлиять, его можно только вычислить.
Я рекомендую попрактиковаться самостоятельно и убедиться, что это работает
Порядок n точки C(7, 8) на самом деле равен 12. Я предлагаю небольшую задачу для практики: попробуйте вычислить 8*C путём сложения 4C + 4C. Затем попробуйте сложить 8C + 8C. Вы получите точку 16C, которая будет равняться 4C!
Это работает буквально как часы. Посмотрите сами:

На данном этапе мы знаем абсолютно всё необходимое, чтобы использовать эллиптические кривые в криптографии!
Небольшое резюме:
-
Все формулы эллиптических кривых идеально работают и на конечных полях. Мы всё ещё можем вычислить любое целое число x * точку. Нам всё ещё нужно выполнить примерно log2(x) операций!
-
Эллиптические кривые теперь имеют конечный набор точек.
-
Теперь у точек есть их собственный порядок n, который начинает работать как модуль или как часы.
-
Чтобы определить эллиптическую кривую, теперь нам нужны три переменные заместо двух: a, b, и p. p называется порядком эллиптической кривой (не путать с порядком n у точек!)
Откуда мы знаем, какие a, b и p использовать? Это определено в стандартах. Стандартов много.
Что используют Bitcoin и Ethereum?
Они использую стандартизованную эллиптическую кривую, которая называется secp256k1. Вот её переменные:
-
a=0
-
b=7
-
p=115792089237316195423570985008687907853269984665640564039457584007908834671663
Довольно большое число! Я думаю, вы начинаете догадываться, почему эллиптические кривые настолько хороши в криптографии.
Пора использовать эллиптические кривые и их свойства на практике!
Часть IV. Практическое применение: алгоритм цифровой подписи (ECDSA)
Алгоритм цифровой подписи на эллиптических кривых (Elliptic Curves Digital Signature Algorithm) работает в точности на этой “алгебре” эллиптических кривых, которую мы рассмотрели в предыдущей части.
Данный алгоритм позволяет кому угодно подписать сообщение, используя Приватный ключ, а кто угодно другой может проверить, что подпись действительно принадлежит подписавшему, зная также Публичный ключ и оригинальное сообщение.
Это ровно то, что происходит в блокчейнах:
У вас есть пара ключей Приватный ключ — Публичный ключ. Все знают ваш Публичный ключ, но никто кроме вас не знает ваш Приватный ключ.
Вы создаёте сообщение по типу “хочу отправить X количество криптовалюты на адрес Y”, дальше вы подписываете его вашим Приватным ключом (используя алгоритм, описанный в этой части), и отправляете в сеть (в случае биткойна, майнерам). Все остальные участники сети (например, майнеры) могут проверить, что сообщение действительно подписали вы, зная ваш Публичный ключ.
Как это работает?
Всё крутится вокруг одной предопределённой точки GP (generator point), лежащей на предопределённой эллиптической кривой. Точка и кривая определены стандартом и их знают все.
Мы можем сгенерировать любое больше рандомное число, и это будет нашим Приватным ключом (PrivateKey)!
Если мы умножим наш PrivateKey на точку GP, мы получим Публичный ключ (PublicKey)!
Итак, PublicKey = PrivateKey * GP:

Да, публичный ключ — это всего лишь точка на кривой.
Как мы уже знаем, мы не можем поделить точку на точку или точку на число. Все возможные операции перечислены в конце Части I.
Итак, не существует эффективного способа вычислить PrivateKey из PublicKey, несмотря на то, что мы знаем точку GP!
Операции деления точки на число не существует! Грубый перебор теоретически может сработать. Но когда у нас по-настоящему огромное количество возможных точек, например, настолько (почти как атомов во вселенной):
115792089237316195423570985008687907852837564279074904382605163141518161494337
Даже если кто-то использует все существующие вычислительные ресурсы на планете, это займёт миллиарды миллиардов лет!
Пройдёмся по необходимым для алгоритма переменным:
Вот список “глобальных” переменных, определённых стандартом:
-
Конфиг эллиптической кривой (числа a, b, p)
-
Точка GP, которая лежит на этой кривой (её x и y координаты)
-
Вычисленный порядок n точки GP. Как мы уже знаем, n — свойство точки GP, такое, что GP*(n+1) = GP, GP*(n+2) = GP, и так далее. Как модуль.
Переменные, которые принадлежат кому-то конкретному:
-
PrivateKey (приватный ключ) - любое большое рандомное число. Держится в секрете его владельцем.
-
PublicKey (публичный ключ) = GP * PrivateKey. Известен всем.
Переменные, которые используются при подписи сообщения:
-
Message (сообщение) — любое целое число, не превышающее n. Обычно используется хэш от строки. Но для простоты пока что ограничим себя целым числом.
-
K - случайное целое число, которое генерируется для одной подписи сообщения. Держится в секрете тем, кто подписывает сообщение. Если кто-то его узнает — с лёгкостью вычислит приватный ключ из подписи!
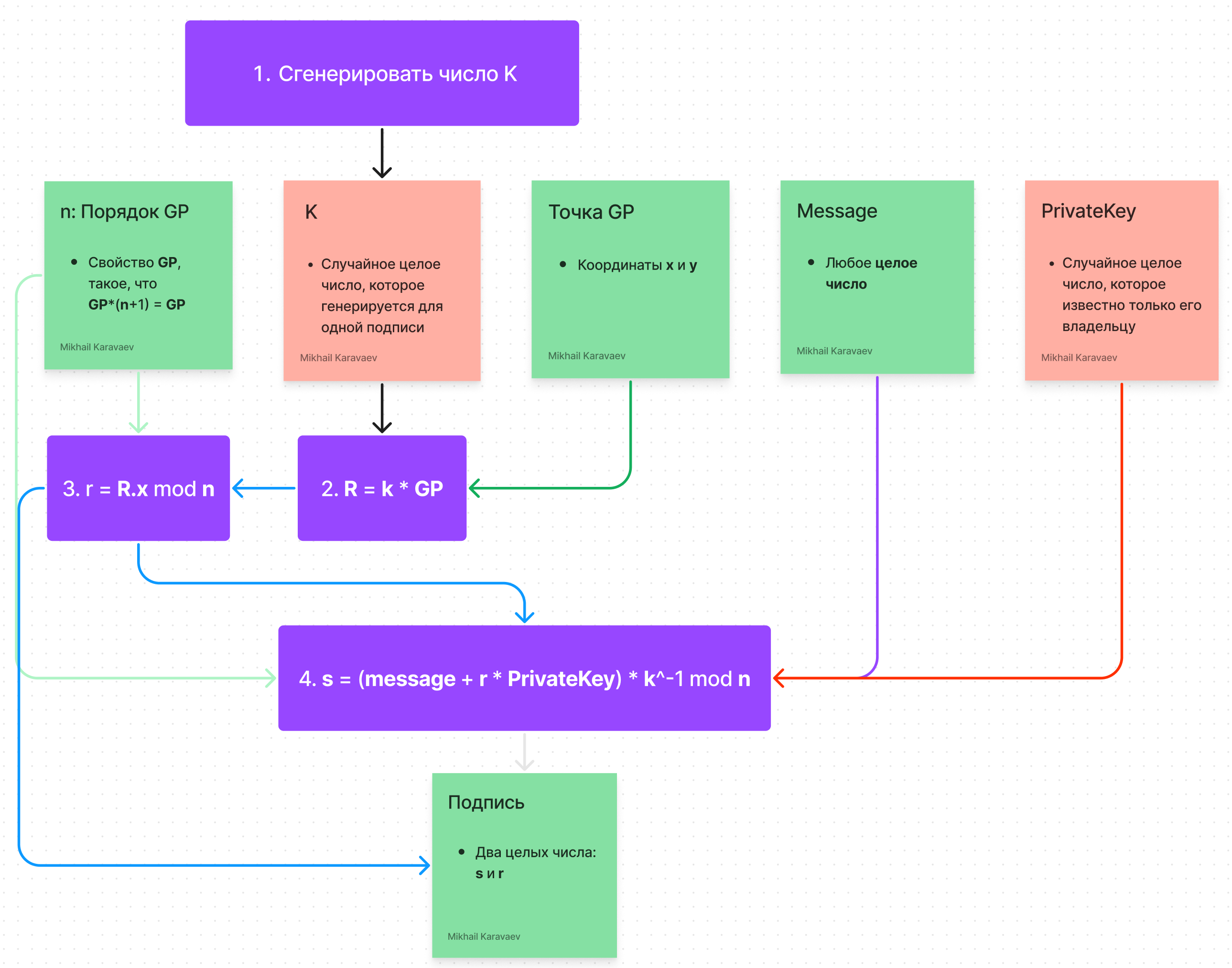
Вот полная картина. Зелёными стикерами обозначены переменные, которые известны всем, а красными — секретные.

Очень много переменных! Хочу обрадовать: это был исчерпывающий список.
Теперь сами алгоритмы подписи и верификации:
Алгоритм подписи сообщения
У нас есть приватный ключ (PrivateKey) и сообщение (message). Чтобы подписать сообщение, нужно:
-
Сгенерировать случайное целое число k. Это должно быть больше число [1, n-1]
-
Вычислить точку R = GP * k.
-
Вычислить число r:

-
Вычислить число s:

Готово! Подпись — это пара чисел (r, s)!
Получается вот такая картина:
Алгоритм верификации подписи
У нас есть публичный ключ (PublicKey) подписавшего, сообщение (message) и подпись (r, s). Чтобы проверить, что подпись верна, нужно:
-
Вычислить число U:

-
Вычислить число V:

-
Вычислить точку C = U * GP + V * PublicKey
-
Если x координата точки C mod n равняется r (C.x mod n == r), тогда подпись корректна. Некорректна иначе.
Вот так всё выглядит:

Совершенно неочевидно.
На самом деле, это небольшой математический трюк.
Немного поиграем с формулами и докажем, что это работает:
В шаге 3 алгоритма верификации мы вычисляем точку C:

Заменим переменные U, V, PublicKey на их определения:


Заметим, что часть GP * s-1 повторяется. Вынесем за скобки:

Посмотрим на определение переменной s в шаге 4 алгоритма подписи и определим s-1:

Подставим в формулу:

Упростим эту часть:

Вот что получилось:

Таким образом, если подпись корректна, то x координата точки C == r (которая по своему определению — та же самая x координата точки GP * k). Все операции под mod n.
Все переменные стандарта secp256k1:
Для эллиптической кривой:
-
a=
0 -
b=
7 -
p=
115792089237316195423570985008687907853269984665640564039457584007908834671663
Для точки GP:
-
x =
55066263022277343669578718895168534326250603453777594175500187360389116729240 -
y =
32670510020758816978083085130507043184471273380659243275938904335757337482424 -
Порядок n =
115792089237316195423570985008687907852837564279074904382605163141518161494337
Готово! Теперь мы знаем АБСОЛЮТНО всё необходимое об ECDSA!
Следующая часть будет самой простой для программистов. Но она не обязательна для всех остальных. Если вы не связаны с программированием, рекомендую сразу перелистать к части VI: Live Demo.
Часть V. Реализация
Небольшие проблемы, которые нужно решить:
-
Необходимо уметь производить базовые арифметические операции на огромных числах. В программировании мы можем очень легко этого достичь, используя длинную арифметику. Наш язык программирования должен поддерживать длинную арифметику, или мы должны использовать какую-нибудь внешнюю зависимость для работы с длинными числами. В примерах этой части для простоты я буду использовать Python, который поддерживает длинную арифметику из коробки. В демо (следующая часть) я буду использовать JavaScript с пакетом BigNumber.js.
-
Следующая проблема — нахождение обратного числа по модулю для огромного числа. Очевидно, что грубый перебор не сработает. Обратное число можно легко найти с помощью расширенного алгоритма Евклида, который имеет сложность O(log2(n)). Python (3.8+) умеет делать это из коробки с помощью встроенной функции pow:
def find_inverse(number, modulus):
return pow(number, -1, modulus)Но если вам нужна реализация с нуля, вы можете её найти в моём Live Demo!
Начинаем писать код!
Нам нужна всего одна простая вещь, связанная с эллиптической кривой: точка. Определим класс Point. В конструкторе сделаем проверку, лежит ли указанная точка на заданной эллиптической кривой:
class Point:
def __init__(self, x, y, curve_config):
a = curve_config['a']
b = curve_config['b']
p = curve_config['p']
if (y ** 2) % p != (x ** 3 + a * x + b) % p:
raise Exception("The point is not on the curve")
self.x = x
self.y = y
self.curve_config = curve_configНам нужно выполнять 3 операции над точками: сравнивать две точки, складывать две точки, умножать точку на любое целое число. Определим метод для проверки равенства двух точек:
def is_equal_to(self, point):
return self.x == point.x & self.y == point.yТеперь определим метод для сложения двух точек, который возвращает точку - результат сложения:
def add(self, point):
p = self.curve_config['p']
if self.is_equal_to(point):
slope = (3 * point.x ** 2) * find_inverse(2 * point.y, p) % p
else:
slope = (point.y - self.y) * find_inverse(point.x - self.x, p) % p
x = (slope ** 2 - point.x - self.x) % p
y = (slope * (self.x - x) - self.y) % p
return Point(x, y, self.curve_config)Напомню, что все формулы перечислены в Части III!
Теперь нужно определить метод для умножения точки на число.
Вот самая прямолинейная реализация:
def multiply(self, times):
point = self
for i in range(times - 1):
point = point.add(self)
return pointНо давайте представим, что нам нужно умножить точку на большое число, например вот это: 115792089237316195. Даже имея скорость в 1 миллиард сложений в секунду, это заняло бы 3.6 года.
И это даже не большое число для нас! Вот большое число:
115792089237316195423570985008687907852837564279074904382605163141518161494337
Вычисление такого умножения данным алгоритмом заняло бы миллиарды миллиардов лет!
Мы можем определить эффективность данного алгоритма как O(n), что совершенно неприемлемо для наших целей. Если вы помните, существует очень простой способ достичь эффективности O(log2(n)), с помощью последовательного удвоения точек:
2P = P+P
4P = 2P + 2P
8P = 4P + 4P
16P = 8P + 8P
32P= 16P + 16P
64P = 32P + 32P
Таким образом, log2(115792089237316195) = 56
log2(115792089237316195423570985008687907852837564279074904382605163141518161494337) = 256
Итак, нам не нужно миллиардов миллиардов лет, чтобы вычислить настолько огромную точку. Нам нужно всего лишь 256 операций сложения!
Один нюанс: чтобы эффективно умножать точку на числа, которые не являются степенями двойки, имеет смысл сохранять все промежуточные точки, чтобы потом скомбинировать их вместе.
Например, чтобы добраться до точки 100P в примере выше, мы больше не можем умножать точку 64P на 2. Точно также мы не можем начать добавлять точку за точкой, поскольку на больших числах это точно так же заняло бы миллиарды миллиардов лет. Вот что имеет смысл сделать:
96P = 64P + 32P
100P = 96P + 4P
Для этих целей, нужно хранить все предыдущие точки, а когда мы больше не можем умножить точку на 2 — по одной находить наибольшие подходящие точки, чтобы как можно скорее добраться до требуемой точки.
Эффективная реализация:
def multiply(self, times):
current_point = self
current_coefficient = 1
pervious_points = []
while current_coefficient < times:
# сохраняем текущую точку в листе предыдущих точек
pervious_points.append((current_coefficient, current_point))
# если можем умножить текущую точку на 2, умножаем
if 2 * current_coefficient <= times:
current_point = current_point.add(current_point)
current_coefficient = 2 * current_coefficient
# если не можем умножить на 2, находим наибольшую подходящую точку, и складываем текущую точку с ней
else:
next_point = self
next_coefficient = 1
for (previous_coefficient, previous_point) in pervious_points:
if previous_coefficient + current_coefficient <= times:
if previous_point.x != current_point.x:
next_coefficient = previous_coefficient
next_point = previous_point
current_point = current_point.add(next_point)
current_coefficient = current_coefficient + next_coefficient
return current_pointНа данный момент мы написали код для всего, что описано до части IV. Теперь реализуем сам алгоритм цифровой подписи из части IV:
Определим переменные стандарта secp256k1:
secp256k1_curve_config = {
'a': 0,
'b': 7,
'p': 115792089237316195423570985008687907853269984665640564039457584007908834671663
}
x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
n = 115792089237316195423570985008687907852837564279074904382605163141518161494337
gp_point = Point(x, y, secp256k1_curve_config)Я использую числа в десятичной системе счисления для простоты восприятия.
Алгоритм для подписи сообщения приватным ключом:
def sign_message(message, private_key):
k = random.randint(1, n)
r_point = gp_point.multiply(k)
r = r_point.x % n
if r == 0:
return sign_message(message, private_key)
k_inverse = find_inverse(k, n)
s = k_inverse * (message + r * private_key) % n
return r, sАлгоритм для проверки подписи:
def verify_signature(signature, message, public_key):
(r, s) = signature
s_inverse = find_inverse(s, n)
u = message * s_inverse % n
v = r * s_inverse % n
c_point = gp_point.multiply(u).add(public_key.multiply(v))
return c_point.x == rВыберем какое-нибудь произвольное число для PrivateKey: 123456789012345
Пусть message будет 12345
Помните, как вычислить публичный ключ из приватного?
private_key = 123456789012345 # любое рандомное число
message = 12345 # любое целое число
public_key = gp_point.multiply(private_key)А теперь попробуем подписать сообщение и проверить:
signature = sign_message(message, private_key)
print('Signature: ', signature)
print('Is valid: ', verify_signature(signature, message, public_key))Работает! Попробуйте сами руками подменить подпись, оригинальное сообщение или ключи, и убедитесь, что алгоритм работает корректно!
Полный код:
import random
def find_inverse(number, modulus):
return pow(number, -1, modulus)
class Point:
def __init__(self, x, y, curve_config):
a = curve_config['a']
b = curve_config['b']
p = curve_config['p']
if (y ** 2) % p != (x ** 3 + a * x + b) % p:
raise Exception("The point is not on the curve")
self.x = x
self.y = y
self.curve_config = curve_config
def is_equal_to(self, point):
return self.x == point.x and self.y == point.y
def add(self, point):
p = self.curve_config['p']
if self.is_equal_to(point):
slope = (3 * point.x ** 2) * find_inverse(2 * point.y, p) % p
else:
slope = (point.y - self.y) * find_inverse(point.x - self.x, p) % p
x = (slope ** 2 - point.x - self.x) % p
y = (slope * (self.x - x) - self.y) % p
return Point(x, y, self.curve_config)
def multiply(self, times):
current_point = self
current_coefficient = 1
pervious_points = []
while current_coefficient < times:
# сохраняем текущую точку в листе предыдущих точек
pervious_points.append((current_coefficient, current_point))
# если можем умножить текущую точку на 2, умножаем
if 2 * current_coefficient <= times:
current_point = current_point.add(current_point)
current_coefficient = 2 * current_coefficient
# если не можем умножить на 2, находим наибольшую подходящую точку, и складываем текущую точку с ней
else:
next_point = self
next_coefficient = 1
for (previous_coefficient, previous_point) in pervious_points:
if previous_coefficient + current_coefficient <= times:
if previous_point.x != current_point.x:
next_coefficient = previous_coefficient
next_point = previous_point
current_point = current_point.add(next_point)
current_coefficient = current_coefficient + next_coefficient
return current_point
secp256k1_curve_config = {
'a': 0,
'b': 7,
'p': 115792089237316195423570985008687907853269984665640564039457584007908834671663
}
x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
n = 115792089237316195423570985008687907852837564279074904382605163141518161494337
gp_point = Point(x, y, secp256k1_curve_config)
def sign_message(message, private_key):
k = random.randint(1, n)
r_point = gp_point.multiply(k)
r = r_point.x % n
if r == 0:
return sign_message(message, private_key)
k_inverse = find_inverse(k, n)
s = k_inverse * (message + r * private_key) % n
return r, s
def verify_signature(signature, message, public_key):
(r, s) = signature
s_inverse = find_inverse(s, n)
u = message * s_inverse % n
v = r * s_inverse % n
c_point = gp_point.multiply(u).add(public_key.multiply(v))
return c_point.x == r
# Тесты начинаются здесь
private_key = 123456789012345 # любое рандомное число
message = 12345 # любое целое число
public_key = gp_point.multiply(private_key)
signature = sign_message(message, private_key)
print('Signature: ', signature)
print('Is valid: ', verify_signature(signature, message, public_key))Итак, полная реализация алгоритма ECDSA с полного нуля заняла всего 100 строк кода. И это абсолютно тот же алгоритм, который является ключевой частью Bitcoin и других блокчейнов!
Часть VI. Live Demo
Как и обещал в начале статьи, публикую Live Demo, использующее только формулы и концепции, рассмотренные в самой статье. Пара заметок:
-
Изначально сообщения могут быть только целыми числами. Но это скучно. Поэтому в демо вы можете по желанию использовать хэш от строки (sha256) в качестве сообщения. Везде используется именно эта схема. Но можете использовать и целое число, как в оригинале.
-
Bitcoin использует слегка другие форматы публичных ключей и подписей.
-
Никогда не используйте ничего из этого в продакшене! Это не безопасно. Базовое правило в криптографии: никогда не реализуй ничего своими руками для прода. Куда проще и безопаснее использовать проверенные решения.
В заключение
Надеюсь, статья была достаточно полезной для вас. По крайней мере я сделал всё, чтобы сделать её полезной. Делитесь ей с друзьями и используйте любые её части где угодно. Только пожалуйста оставьте ссылку на саму статью.
Также есть английская версия.


