Пирамиды не на Марсе: изучение формы нанокристаллических кластеров под слоем графена

Очень многие свойства, а следовательно и способы применения чего-либо зависят от формы этого объекта. Все очень просто и столько же логично: круглые колеса будут катиться лучше, чем квадратные, а крылья самолета имеют определенную форму, улучшающую аэродинамику. Даже обыкновенные карандаши имеют форму шестиугольника, чтоб было удобнее держать в руке при письме и не искать его по всей квартире под всеми диванами и шкафами в позе человека, впервые запустившего Dark Souls. Изменение формы может привести к изменению свойств, а если эти изменения контролировать, то можно получить определенные, нужные вам, свойства. Именно этим и занялись ученые в рассматриваемом нами сегодня исследовании. Они создали модель «постоянная эластичность» для нанокристаллических кластеров меди под графеновой мембраной. Как и зачем ученые «намазали» медь графеном, какие результаты показали практические эксперименты, сходятся ли они с предварительными расчетами и что этот «бутерброд» в нанометровом масштабе значит для науки? Ответы на эти вопросы ждут нас в докладе исследовательской группы. Поехали.

Основа исследования

Как заявляют сами ученые, нет ничего важнее структуры и формы функциональных кристаллов (у ученых свои жизненные приоритеты, придираться не будем). Во время синтеза этих маленьких объектов возможны некие отклонения от равновесной структуры, что может быть как очень малоприятным минусом или же большим плюсом. Если понять саму суть равновесной структуры, можно научиться лучше понимать эти структуры, а в следствии и манипулировать ими.

Важную роль в этом играют нанокристаллы (НК), которые делятся на несколько классов: неподдерживаемые трехмерные НК, получаемые путем жидкофазного синтеза, и поддерживаемые трех- и двухмерные НК, получаемые осаждением на поверхности подложки.

Если к этому всему подключить наше любимое слово «квантовая», то мы узнаем следующее: для квантовых точек, т.е. поддерживаемых трехмерных НК, сформированных посредством несоответствия решетки внутри гетероэпитаксии*, крайне важную роль в управлении формой играет деформация.

Гетероэпитаксия* — вид эпитаксии (нарастание одного кристаллического материала поверх другого при низких температурах), когда растущий слой отличается от подложки по химическому составу.

В данном исследовании ученые рассматривают новый тип трехмерных нанокристаллов (кластеров), которые располагаются под слоистым материалом. Таким образом эти НК сжимаются под одним или несколькими монослоями (сверху) и совокупностью полубесконечных слоев (снизу).

Зачем это делают ученые, спросите вы. Они ответят: целью сего исследования является разработка и анализ модели постоянной эластичности (ПЭ), которая соединяет в себе энергию деформации верхнего графенового слоя, адгезию и поверхностные энергии Cu (меди), графена и графита, что позволяет контролировать равновесную форму участков поверхность/инкапсулированные кластеры.

Ученым удалось создать такую модель, после чего они проверили ее жизнеспособность не на бумаге, а в реальности. Какие результаты показал анализ, и какие расхождения наблюдались между теорией и практикой рассмотрим далее.

Подготовка к исследованию

В самом начале необходимо было подготовить графит для взаимодействия с нанокластерами меди. Для этого на его поверхности были созданы дефекты с помощью бомбардировки Ar+. После этого атомы Cu сталкивались с поверхностью графита, проникая через некоторые дефекты и оказывались уже под поверхностью графита. Во время сего действа графитовая подложка нагрета до 600-800 К. Такой температурный режим выбран не просто так: островки (кластеры) Cu на поверхности графита начинают грубеть при температуре 550-600 К, посему разрыв связи Cu-Cu должен быть легко достигнут при 600 К и выше. В результате острова меди сформировались в данном исследовании при температуре 800 К.

Изображение №1

На снимке СТМ 1а мы видим не пирамиды на поверхности красной планеты, а те самые островки меди, СТМ профиль которых показан на 1а’.

Ученые направляют наше внимание на форму этого медного острова: шестиугольник с плоской вершиной. Сплющенность вершины и, соответственно, дна говорит об ограниченности центральной части острова слоем подложки (снизу) и слоем графена (сверху). Также мы видим склоны, формирующие кольцо вокруг плоской вершины. По данным наблюдений толщина углеродного слоя на данных островах может составлять несколько монослоев графена, до трех.

Далее ученые провели анализ формы данного острова (1b). Стало понятно, что высота (h) масштабируется практически идентично с шириной кольца (a). При этом склоны (h/a), то есть уклон сторон, постоянны при разных размерах. А вот диаметр, в отличие от ширины кольца, масштабируется с высотой плохо, то есть соотношение сторон d/h не является постоянным. На графике 1с показано соотношение высоты и ширины кольца, а на графике 1d — высоты и ширины верхушки острова. При этом суммарно было проанализировано порядка 140 островов меди.

Как реально обстоят дела с нанообразованиями меди под слоем графена нам теперь понятно. После этих наблюдений ученые перешли к созданию своей модели постоянной эластичности (ПЭ).

Модель ПЭ

В процессе моделирования ученые решили применить аппроксимацию (приближение) формы острова меди, посему использовалась не гексагональная пирамида, а цилиндрическая. Медный цилиндр растет между мембраной из одного/нескольких монослоев графена и графитовой подложкой.

Предполагается, что графитовая подложка жесткая, а покрывающий слой (над островами меди) подвергается упругим деформациям растяжения и сгибания, что позволяет подстроиться под растущий остров.

Небольшое уточнение терминов: в дальнейшем в своем труде ученые именуют островами совокупность кластера Cu, деформированной графеновой мембраны и графитовой подложки, а кластерами — лишь центральную металлическую часть.

Важным элементом формы островов являются наклоны сторон. Эти склоны значительно меньше, чем у низкоиндексных (111) или (100) Cu-плоскостей, которые естественным образом примыкают к верхней грани (111) для поддерживаемого кластера Cu. Из этого следует вывод, что кольцевое пространство, заполненное медью, не является энергетически жизнеспособной конфигурацией из-за поверхности с высоким индексом и поверхностной энергией Cu.

Следующей важной особенностью является наличие складок кольца, одну из которых можно увидеть в нижнем левом углу на 1а. Подобные деформации говорят о том, что мембрана (покрывающий слой) не поддается влиянию растяжения нижележащего материала, что ограничивает его складывание.

Энергия системы (Π) может быть смоделирована как сумма энергий упругой деформации искаженной графеновой пленки (U_e) и совокупности переменных, представляющих интерфейсные и поверхностные (IS — interface/surface) компоненты общей энергии системы. К интерфейсам и поверхностям относятся: чистая медь, графен – графит (GnGt), медь – графен и медь – графит (обозначение для обоих — CuG). Вышеперечисленному соответствуют следующие IS энергии:

• затраты энергии, связанные с поверхностной энергией Cu, U_Cu и потерей адгезии Gn – Gt, U_GnGt;
• снижение энергии, связанное с адгезией Cu – Gn и Cu – Gt, U_GnGt.

В совокупности они будут именоваться общим термином — U_IS. Ниже представлена формула общей энергии:

Π = U_Cu + U_GnGt + U_CuG + U_e

Равновесная форма была получена путем минимизации Π для фиксированного объема (V) кластера Cu.

Далее были рассчитаны U_IS, то есть интерфейсные и поверхностные компоненты общей энергии системы. Каждый такой компонент можно выразить в виде суммы продуктов поверхностной энергии (γ) или энергии адгезии (β), умноженной на соответствующую площадь.

Таблица №1: формулы вычисления U_IS (слева) и вводные данные (справа).

Значения γ и β были получены посредством теории функционала плотности. А (111) ориентация кластера Cu была получена из экспериментальных данных.

Далее ученые вывели значение U_e посредством расчетной модели SLBT (блистерный тест с цилиндрическим стержнем с плоской вершиной), в которой цилиндрический стержень движется вверх через отверстие в твердой поверхности, прижимаясь к упругой мембране и деформируя ее.

Мембрана подвергается деформации растяжения и сгибания. В модели SLBT эти два типа деформации аппроксимируются как независимые вклады. Расчеты показали, что деформация сгибания достаточно мала при учете размеров экспериментальной структуры, потому моделирование общей энергии упругости мембраны (U_e) возможно было только с учетом деформации растяжения.

На рост острова кольцевое пространство может реагировать без ограничений, однако адгезия между частью графена на вершине острова и медью может препятствовать боковому растяжению графена. Если же растяжение протекает свободно, то эта часть может также свободно деформироваться поверх вершины острова.

Учитывая данное утверждение была выведена формула U_e (№5 в таблице 1). По ней мы можем понять, что значение U_e зависит от коэффициента Пуассона (v), модуля продольной упругости (Y) и толщины графена (t). Значение v было 0.165, Y — 1.1 ТПа, поскольку это соответствует экспериментальным значениям плотности дефектов (7.3 ± 0.4)х10³ мкм^-2.

Касательно толщины графена мы с вами уже знаем, что графен поверх островов может быть толщиной более одного монослоя. Это позволяет вычислить толщину верхнего слоя изучаемой структуры по формуле t = L·t_GML, где L это количество слоев графена, а t_GML равен 0.34 нм (межслоевое расстояние в кристаллическом графите).

Результаты исследования

И так. С данными наблюдений разобрались, с расчетной частью тоже, пора приступить к результатам анализа всего этого в совокупности.

Учитывая формулы U_IS и U_e, а также данные из таблицы 1 (справа), Π становится функцией только трех независимых параметров — a, h, и d. Эту проблему можно решить путем точного установления значения объема кластера V = πhd²/4, что позволяет ликвидировать либо h, либо d. Таким образом получится только два параметра, а не три: Π = Π(a, h) или Π = Π(a, d). Для демонстрации ученые использовали Π(a, h), а объем кластера был взят из используемых данных — 〈V_exp〉 = 4х10⁴ нм³ (изображение №2).

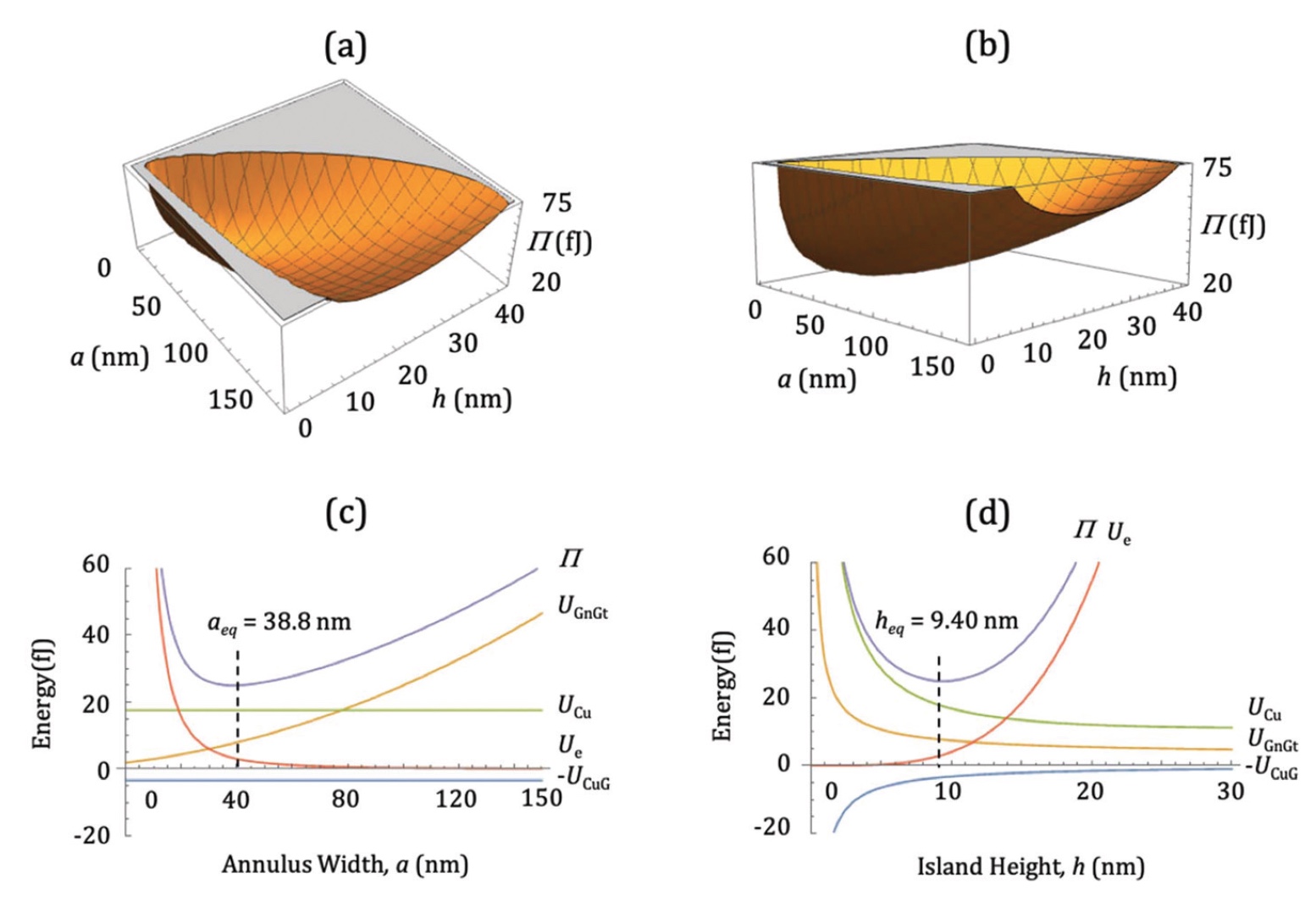
Изображение №2

Ученые отмечают крайне важный момент: существует определенное минимальное значение Π, что является состоянием равновесия. При таком минимуме модель постоянной эластичности предсказывает следующие значения: a_eq = 38.8 нм, h_eq = 9.4 нм и d_eq = 73.6 нм. В экспериментах острова, которые были близки по показателям к 〈V_exp〉, имели следующие параметры: 〈a_exp〉 = 31 ± 11 нм, 〈h_exp〉 = 7.3 ± 2.6 нм и 〈d_exp〉 = 88 ± 21 нм. Как мы видим, данные теоретические и практические очень хорошо согласуются.

Графики 2с и 2d показывают два ортогональных разреза через Π(a, h), каждый из которых проходит через глобальный минимум.

Вышеописанные процессы можно повторить во всем диапазоне экспериментально наблюдаемых объемов кластеров (1.8х10³ нм³ ≤ V ≤ 6.9х10⁵ нм³). Посему можно провести сравнение размеров островов, прогнозированных моделью и наблюдаемых в экспериментах. Для более простого сравнения модели и эксперимента используется соотношение размеров островов и значения h (изображение №3).

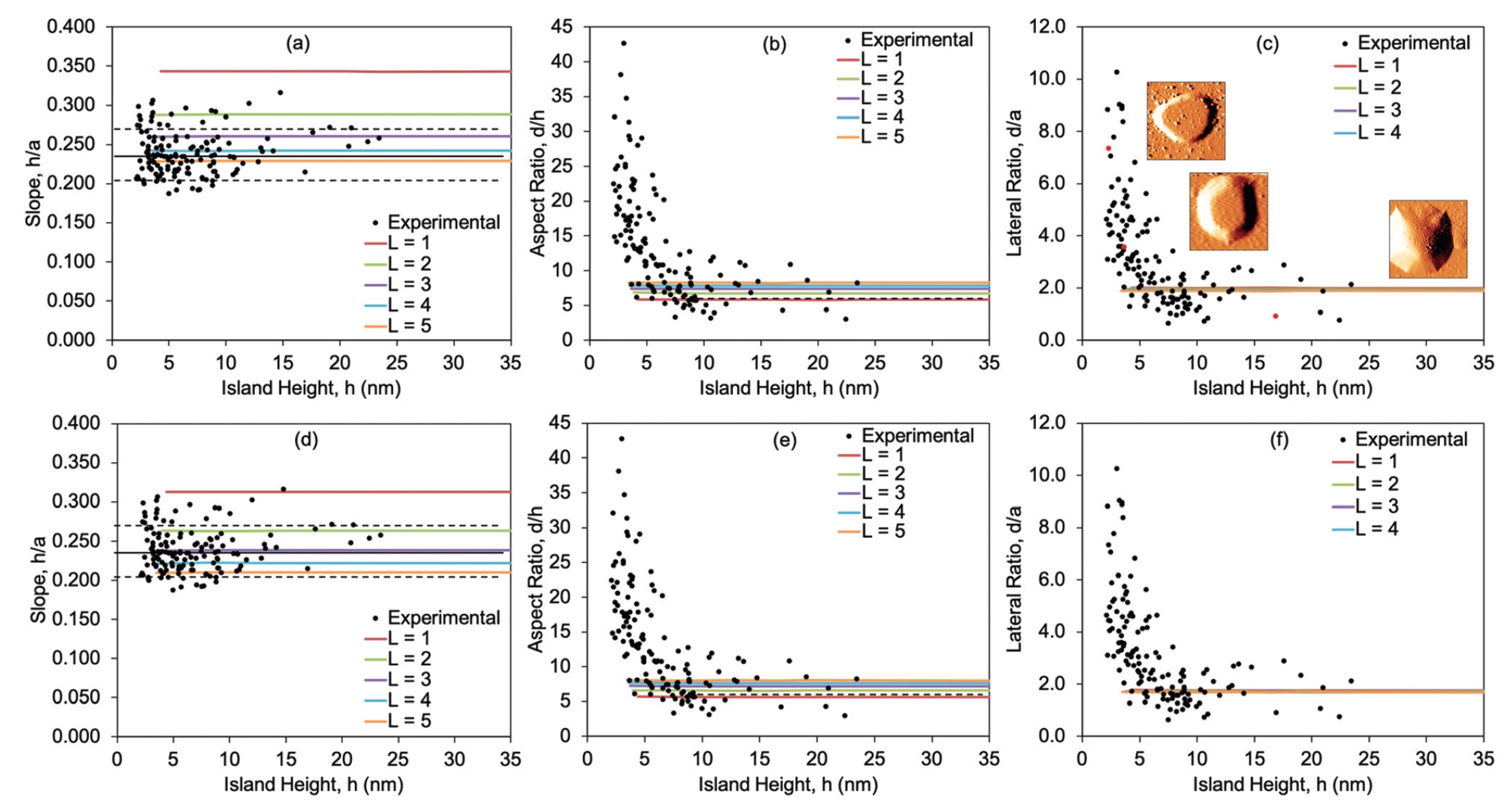
Изображение №3

На графиках выше показаны значение h/a, d/h и d/a как для модели, так и для эксперимента. Графики 3а—3с это сравнение экспериментальных данных и модели SLBT, в которой расширение мембраны протекает без ограничений, а 3d—3f это уже экспериментальные данные и модель с ограниченным расширением.

Значение h/a в экспериментах постоянно и равняется 0,24 ± 0,03 во всем диапазоне размеров островков. В теории использовался объем кластеров 1 ≤ L ≤ 5, а лучшее согласование показателей теории и практики было обнаружено при L = 4.

В значении d/h (и параллельно d/a) наблюдаются необычные изменения. Как видно с графика 3b экспериментальное значение d/h начинается с 40, но потом начинает резко снижаться с увеличением значения h. Когда h достигает ≈ 10 нм, значение d/h выравнивается до 7,3 ± 2,8 (горизонтальная пунктирная линия на 3b). Теоретическая же модель показала значения d/h в диапазоне от 5,6 до 8,0 для L = 1…5.

С фиксированной моделью SLBT показатели очень схожи со свободной моделью SLBT. Единственное значимое отличие заключается в том, что при каком-либо значении L соотношение h/a в фиксированной модели немного меньше, чем в свободной модели. Таким образом, наилучшее согласование теории и практики в случае фиксированной модели SLBT проявляется при L = 3.

Для более детального ознакомления с исследованием настоятельно рекомендую заглянуть в доклад исследовательской группы.

Эпилог

Что мы имеем в совокупности? Ученые создали теоретическую модель, которая отлично согласуется с экспериментальными данными. Данная модель демонстрирует, что форма нанокристаллических кластеров меди сохраняется, по крайней мере в случае масштабов, когда деформация сгибания не очень сильна. Также исследователи выяснили, что расслаивание в кольцевом пространстве является реакцией на смещение мембраны (покрывающего слоя) вверх исключительно в центральной области (внутренней окружности кольца) и отражает свойства графена/графита, а не самой меди.

Помимо этого было установлено, что подобные вышеописанные наблюдения реальны для систем, в которых металлический кластер встроен вблизи поверхности слоистого трехмерного материала или под поддерживаемой двумерной мембраной, но лишь при условии равновесной формы. В таком случае, необходимо (и возможно, как показали результаты) использовать механические свойства мембраны, адгезию и поверхностные энергии для прогнозирования равновесной формы инкапсулированного тела, то есть металлических кластеров (в данном труде медных). Этот принцип работает и в обратном направлении — можно узнать энергетические и механические свойства посредством измерений размеров кластеров. Ученые приводят короткий пример: измерив h и а и зная механические свойства мембраны, можно установить энергию адгезии мембрана-подложка.

Наилучшим образом данный труд может быть использован в современных технологиях, которые опираются на слоистые материалы — графит или его производные, как графен. А если учесть, что тенденция к уменьшению физических размеров электронных устройств пока еще не идет на спад, то такие исследования имеют большую цену, а потому будем ждать новых шокирующих открытий и удивительных экспериментов.

Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята!

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас оформив заказ или порекомендовав знакомым, 30% скидка для пользователей Хабра на уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps от $20 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps до лета бесплатно при оплате на срок от полугода, заказать можно тут.

Dell R730xd в 2 раза дешевле? Только у нас 2 х Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 ТВ от $249 в Нидерландах и США! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?