
Выполнение бочки никак не помогает гражданскому самолету довезти своих пассажиров до места назначения или истребителю в бою, но требует, при правильном выполнении, задействовать все органы управления самолетом: элероны, руль высоты и руль направления.
В данной публикации изложено описание процесса поворота самолета на 360 градусов вокруг продольной оси без снижения с точки зрения такой науки, как динамика полета, и приведено описание того, как можно заставить ваш самолет сделать бочку правильно.
Введение
После завершения активной фазы очередного проекта у меня с коллегой по беспилотной деятельности возник вопрос, чем заняться пока новые проекты не заняли все свободное время. В ответ на вопрос, заданный пустоте, мы получили очень конкретный ответ «сделай бочку (do a barrel roll)». И правда: бочка это машина Голдберга в авиации, одновременно сложная, практически (в воздушном бою) бесполезная и приносящая исключительно эстетическое удовольствие фигура пилотажа. Так почему бы не научить авиамодель делать бочку в автоматическом режиме, даже Google её делает.
Прежде чем начать практическую реализацию мы решили изучить это процесс с привлечением компьютерных моделей, и вот что из этого получилось.
Немного теории
Для начала немного о том, почему самолеты летают и о том, как положение самолета описывается относительно поля тяготения. Самолет держит в воздухе подъемная сила, назовем ее Y, которая создается на крыле, но вот какая штука, эта сила появляется только при обдуве крыла набегающим потоком воздуха, соответственно, нужно самолет разогнать. Можно, конечно «разбежавшись прыгнуть со скалы», потратить часть потенциальной энергии поля тяготения земли на разгон и даже зависнуть на мгновенье, но неразрывно с подъемной силой возникает аэродинамическое сопротивление, назовем эту силу X, которое будет самолет тормозить, и подъемная сила будет падать, а вместе с ней и мы. Падать мы будем под действием силы тяжести G. Для противодействия силе сопротивления у всех нормальных самолетов есть двигатель, он создает силу тяги P, которую можно использовать для преодоления силы сопротивления. Простейшая кинематическая модель самолета описывает его движение как перемещение материальной точки в поле тяготения земли. В горизонтальном полете с постоянной скоростью сила тяжести уравновешена подъемной силой крыла Y = G, а сила сопротивления — тягой двигателя X = P.
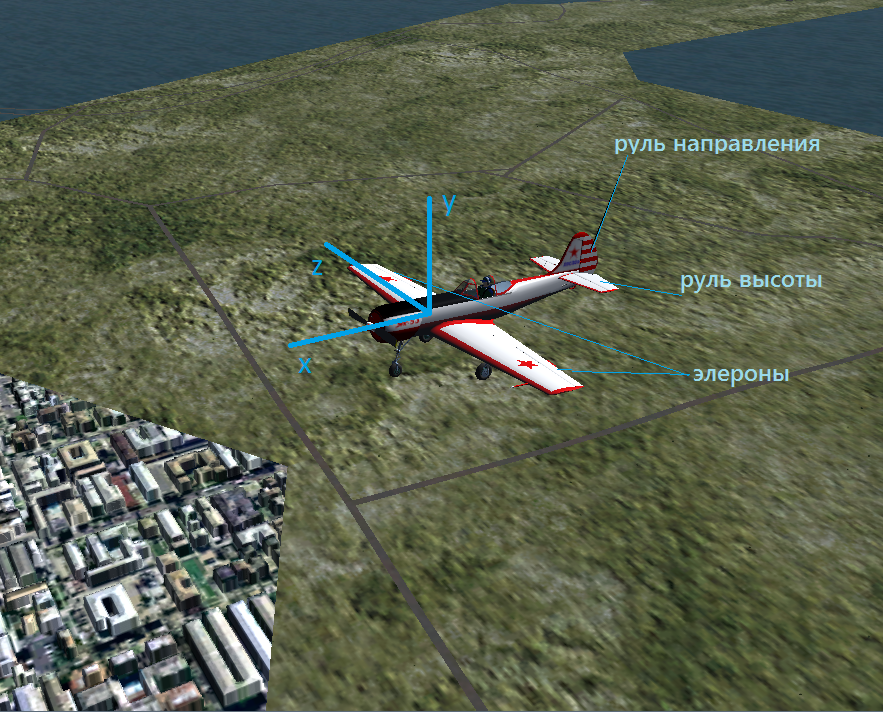
Если посмотреть на материальную точку под микроскопом, она превратится в материальное тело. Оно и к лучшему: мы можем разглядеть у самолета фюзеляж, крыло, хвостовое оперение, которое состоит из горизонтального стабилизатора и вертикального киля. На левой и правой консолях крыла расположены элероны, на горизонтальном хвостовом оперении — руль высоты, на вертикальном — руль направления. Если всем этим усиленно вертеть, аппарат начнет маневрировать, и задача сделать бочку сведется к тому, по какому закону изменять положение органов управления для достижения необходимой траектории движения аппарата в пространстве и относительно его собственных осей.
Движение аппарата в пространстве невозможно описать только при помощи связанной с самолетом системой координат, ведь нам интересно положение аппарата относительно земли. Для этого вводится система координат, которая называется «местная земная система координат». Ось X этой системы находится в горизонтальной плоскости и направлена на географический север. Oсь Y направлена вертикально вверх. Ось Z дополняет их до правой тройки векторов. Расположение связанной системы координат относительно местной земной системы определяется углами крена, тангажа и рыскания. Угол между продольной осью самолета (в нашем случае ось x связанной СК) и горизонтальной плоскостью XZ называется углом тангажа, он изменяется при отклонении руля высоты. Угол между осью z связанной СК и осью Z местной земной СК, повёрнутой так, что угол рыскания равен нулю, называется углом крена, он изменяется при отклонении элеронов. Угол между осью X местной земной СК и проекцией оси x связанной СК на горизонтальную плоскость XZ называется углом рыскания, отсчитывается против часовой стрелки от оси X местной земной СК. Такой формализации нам должно быть достаточно для описания движения самолета при выполнении бочки, и пусть, мы не воспользуемся далее буквенными обозначениями осей, всегда полезно повторить основы.
Инструментарий
Для моделирования движения аппарата мы используем инструментарий, который предоставляет программа для моделирования динамики летательных аппаратов с открытым исходным кодом JSBSim. Вывод графиков доверим gnuplot, а визуализацию маневров самолета FlightGear. В качестве базовой динамической модели возьмем истребитель North American P-51 Mustang: его маневренности будет достаточно для выполнения бочки. Для визуализации будем использовать менее агрессивный, спортивный самолет ЯК-53.
fgfs --native-fdm=socket,in,60,,5500,tcp --fdm=external --timeofday=noon --aircraft=Yak-53 --disable-sound --disable-real-weather-fetch --disable-clouds3d --disable-cloudsВ этой строке первые параметры указывают внешний источник данных о динамике самолета при запуске симулятора. Параметр aircraft задает требуемую модель аппарата. Остальные параметры не обязательны, их значения можно найти здесь. Полезные сочетания клавиш:
«V»-изменить вид модели
Shift+Esc – перезапуск FlightGear с сохранением параметров командной строки
Ctrl+«R» — запуск записи полета для повторения того, что получилось.
Вот собственно и все, что нам понадобится в симуляторе FlightGear. Вернемся к программе моделирования динамики JSBSim. В каталоге JSBSimaircraft находятся динамические модели самолетов. В каталоге JSBSimengine находятся динамические модели двигателей и винтов. Динамические модели самолетов хранятся в отдельных каталогах в файлах вида name*.xml. В конце каждого файла есть секция, отвечающая за вид выходных данных при моделировании. Если мы хотим, чтобы вывод был в виде, подходящем для визуализации во FlightGear, то она должна выглядеть так:
Если же мы хотим сохранять данные в файл, то так:
Запускать процесс моделирования удобно при помощи пакетного файла, расположенного в корневой папке JSBSim, строкой
JSBtest.bat *имя_скриптас содержанием
rem Remove the old result file del /Q aircraftp51dResults%1.csv rem Run the test DebugJSBSim --script=aircraftp51dscripts%1.xml --outputlogfile=aircraftp51dResults%1.csv>JSBSim.out --realtime rem Generate gnuplot to the screen gnuplot aircraftp51dplots%1.p Данный файл удаляет предыдущие результаты моделирования, запускает скрипт, расположенный по адресу JSBSimaircraftp51dscripts, а затем запускает отрисовку полученных данных при помощи gnuplot. Параметр realtime необходимо указывать в случае, когда данные из JSBSim хочется получать в режиме реального времени, например, при визуализации во FlightGear.
Посмотрим на содержание файла скрипта:
sim-time-sec ge 0.0 sim-time-sec ge 0.5 sim-time-sec ge 2.95 Для правильного запуска в третьей строке указывается модель самолета, который будет смоделирован, и путь к инициализационному файлу с содержанием
-1 325.0 210.0 42.3769 -70.9993 Осталось только рассмотреть содержание файла для построения графиков через gnuplot:
set autoscale # scale axes automatically unset log # remove any log-scaling unset label # remove any previous labels set xtic auto # set xtics automatically set ytic auto # set ytics automatically set tics font "Arial, 16" set key font "Arial, 16" set xlabel font "Arial, 16" set ylabel font "Arial, 16" # If you have graphical capabilities, you can plot on your screen # if none of the other terminals is specificed. # This is how to output the plot in PostScript format #set terminal postscript portrait enhanced color lw 1 "Helvetica" 14 size 8.5,11 # This is how to output the plot in PNG format #set terminal png size 1280,960 #set output "aircraft/p51d/results/plot.png" # This is how to output the plot in PDF format. (Not available on Mac) #set terminal pdfcairo color size 8.5,11 #set output " aircraft/p51d/results/plot.pdf" set multiplot title "" set size 1,0.30 set lmargin 10 set xrange [0:4] set ytic auto set origin 0.0,0.00 set xlabel "Время,с" set ylabel "Высота, м" plot "aircraft/p51d/results/trim-cruisep51d.csv" using 1:($43*0.3048) title "" with lines set origin 0.0,0.33 set ylabel "Угол тангажа, °" set xlabel "" plot "aircraft/p51d/results/trim-cruisep51d.csv" using 1:33 title "" with lines set origin 0.0,0.66 set ylabel "Угол крена, °" set xlabel "" set yrange [-180:180] set ytics 60 plot "aircraft/p51d/results/trim-cruisep51d.csv" using 1:32 title "" with lines unset multiplot # exit multiplot mode pause -1 "Press ENTER to continue" Данный файл формирует и выводит изображение на экран трех графиков: угла крена, тангажа и высоты от времени. Данные для построения берутся из файла *имя_скрипта.csv. Попутно, имперские единицы переводятся в привычные нам, метрические. Можно изменить файл для вывода в форматах PostScript, PNG или PDF, раскомментировав соответствующие строки.
Вот, в общем-то, и весь процесс подготовки инструментов для самостоятельного моделирования и отображения движения самолета.
Моделирование и результаты
Если вообразить «сферический», а точнее идеальный самолет, у которого оси связанной системы координат совпадают с главными осями эллипсоида инерции и органы управления создают моменты каждый относительно только одной из осей, можно на качественном уровне понять, как аппарат будет двигаться при отклонении органов управления. Допустим, самолет летит в горизонтальном полете; отклоняя элероны в противоположные стороны, мы изменяем величину подъемной силы на консолях крыла, что приводит к возникновению момента сил относительно оси x, и аппарат начнет вращаться вокруг этой оси. Для выполнения бочки это как раз, то что нам нужно. Составляем скрипт, в котором элероны максимально отклонены в течение 2.45 секунд, а затем возвращаются в исходное положение:
sim-time-sec ge 0.0 sim-time-sec ge 0.5 sim-time-sec ge 2.95 
Результаты моделирования приведены на графике:
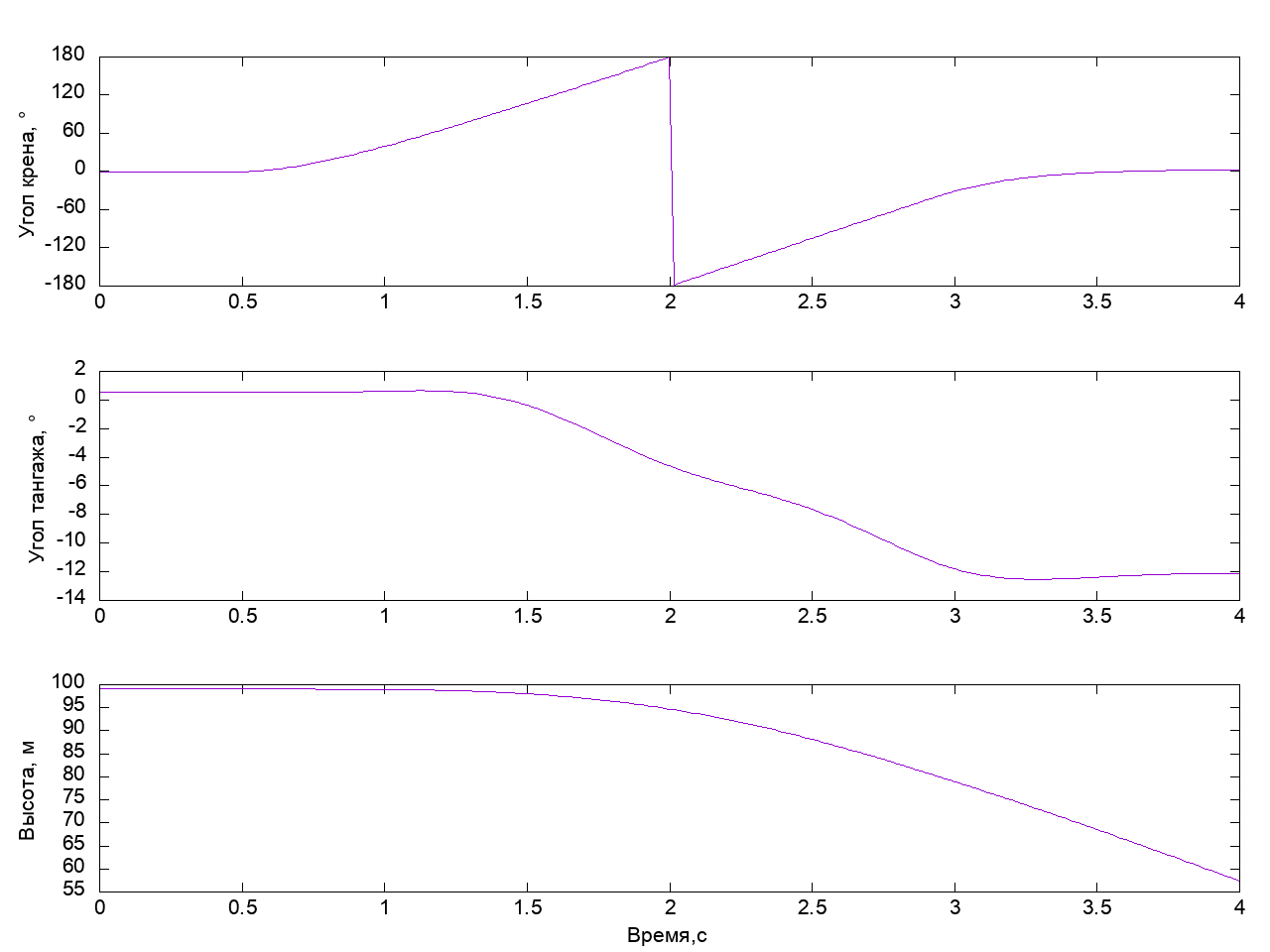
Видно, что самолет повернулся на 360 градусов по крену, однако, сделал этот маневр со снижением в 40 метров и наклонил нос на 14 градусов — это пример совсем не годной бочки.
И правда, если вспомнить, что самолет издалека это материальная точка, то при вращении проекция подъемной силы на направление силы тяжести уменьшается и самолет начинает снижение, а нам этого совсем не нужно, ведь мы хотим выполнить красивую бочку без снижения. Для этого, до того, как мы начали отклонять элероны, нужно создать запас вертикальной скорости. Берем штурвал на себя — отклоняется руль высоты — возникает момент силы относительно оси z. Нос самолета поднимается, и мы начинаем набирать высоту — в этот момент пора начинать вращение. Добавляем в скрипт отклонение руля высоты на 40 процентов за 0.4 секунды до начала отклонения элеронов и возвращаем его в нейтральное положение. За 0.2 секунды до окончания вращения берем штурвал полностью на себя, чтобы устранить опускание носа самолета:
sim-time-sec ge 0.0 sim-time-sec ge 0.1 sim-time-sec ge 0.5 sim-time-sec ge 2.75 sim-time-sec ge 2.95 
Смотрим, что получилось:
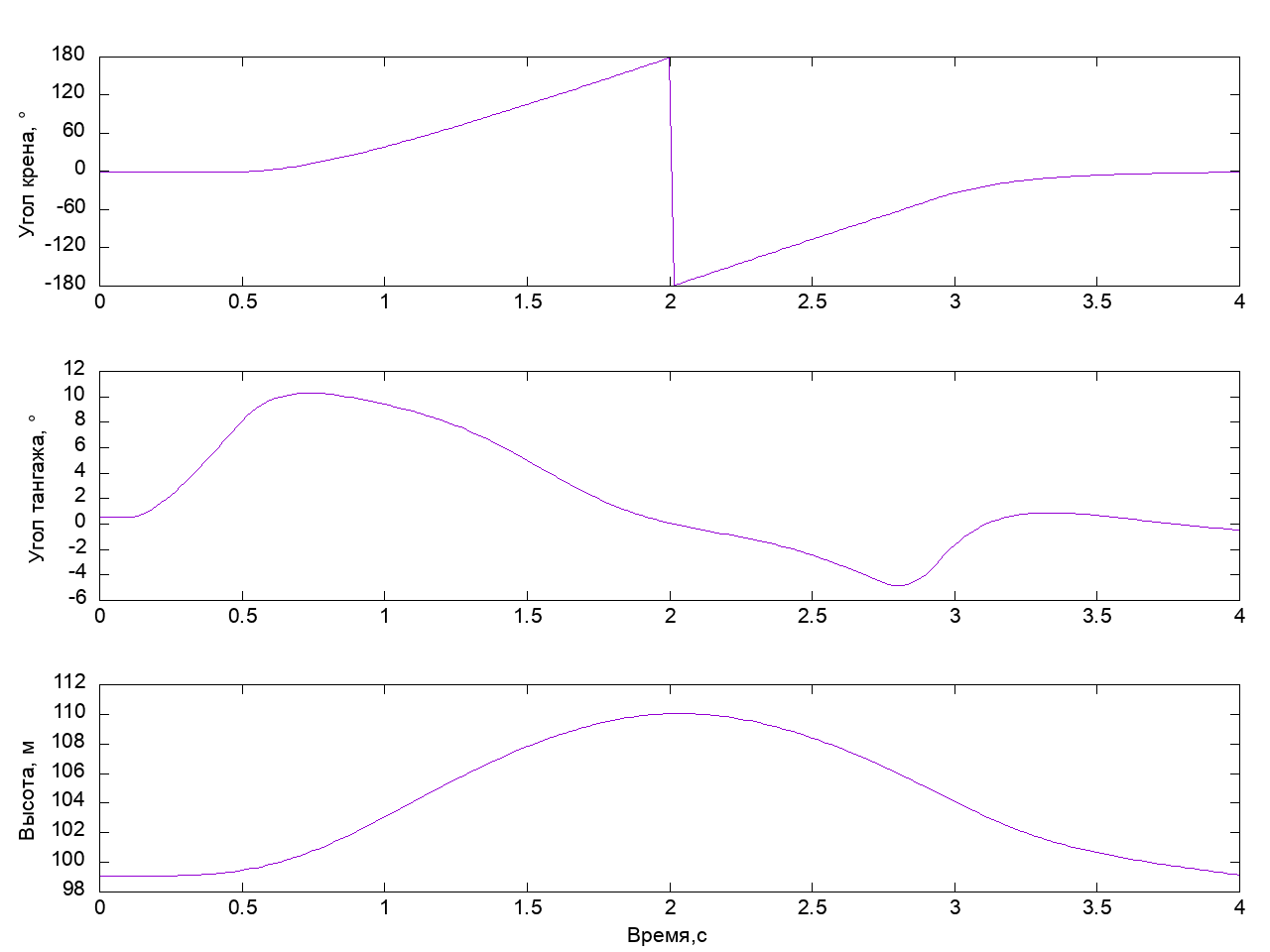
Вот она — вполне приличная, быстрая бочка. Если бы мы вернули руль высоты в нейтральное положение немного позже, аппарат набрал бы небольшую высоту и после отклонения элеронов пошел бы в разворот. Комбинация «штурвал на себя» и «отклонение элеронов» приводит к тому, что подъемная сила крыла при наклоне аппарата начинает действовать по нормали к текущей траектории аппарата и искривляет её тем сильнее, чем более отклонен руль высоты. Можете попробовать сами и убедиться в этом.
Предыдущая бочка была выполнена без снижения, угол тангажа на выходе из бочки не сильно отличался от исходного. Однако, высота в процессе выполнения изменялась на 12 метров. Попробуем более активно применить органы управления, чтобы минимизировать заброс по высоте в процессе выполнения фигуры. Чтобы не вертеть органами управления самолетом абы как, заглянем в Википедию и посмотрим, как нам рекомендуют делать бочку. Основная мысль выполнения идеальной бочки состоит в том, что нужно сохранить продольную ось самолета в горизонтальной плоскости. Для этого попеременно используются руль высоты и руль направления. В начале бочки, как обычно, мы используем руль высоты, чтобы набрать вертикальную скорость. Отклоняем элероны – начинаем вращение. Когда самолет поворачивается вокруг продольной оси руль высоты и руль направления меняются местами. По достижению величины угла крена около 90 градусов отклонение руля направления приведет к поднятию или опусканию носа самолета в вертикальной плоскости. В связи с этим, отклоняем руль направления так, чтобы предотвратить опускание носа. Далее, когда угол крена достигает 180 градусов, нужно отклонить руль направления от себя чтобы в перевернутом полете удержать нос самолета в горизонтальной плоскости. При дальнейшем повороте повторяем отклонения руля направления с противоположным знаком при угле крена вблизи – 90 градусов и завершаем бочку небольшим отклонением руля высоты «на себя». Все эти этапы выражены в скрипте, приведенном ниже:
sim-time-sec ge 0.0 sim-time-sec ge 0.0 sim-time-sec ge 0.5 sim-time-sec ge 0.6 sim-time-sec ge 1.4 sim-time-sec ge 1.6 sim-time-sec ge 1.65 sim-time-sec ge 2.35 sim-time-sec ge 2.6 sim-time-sec ge 2.8 sim-time-sec ge 2.75 sim-time-sec ge 2.95 sim-time-sec ge 3.0 
Запускаем и смотрим, что получилось:
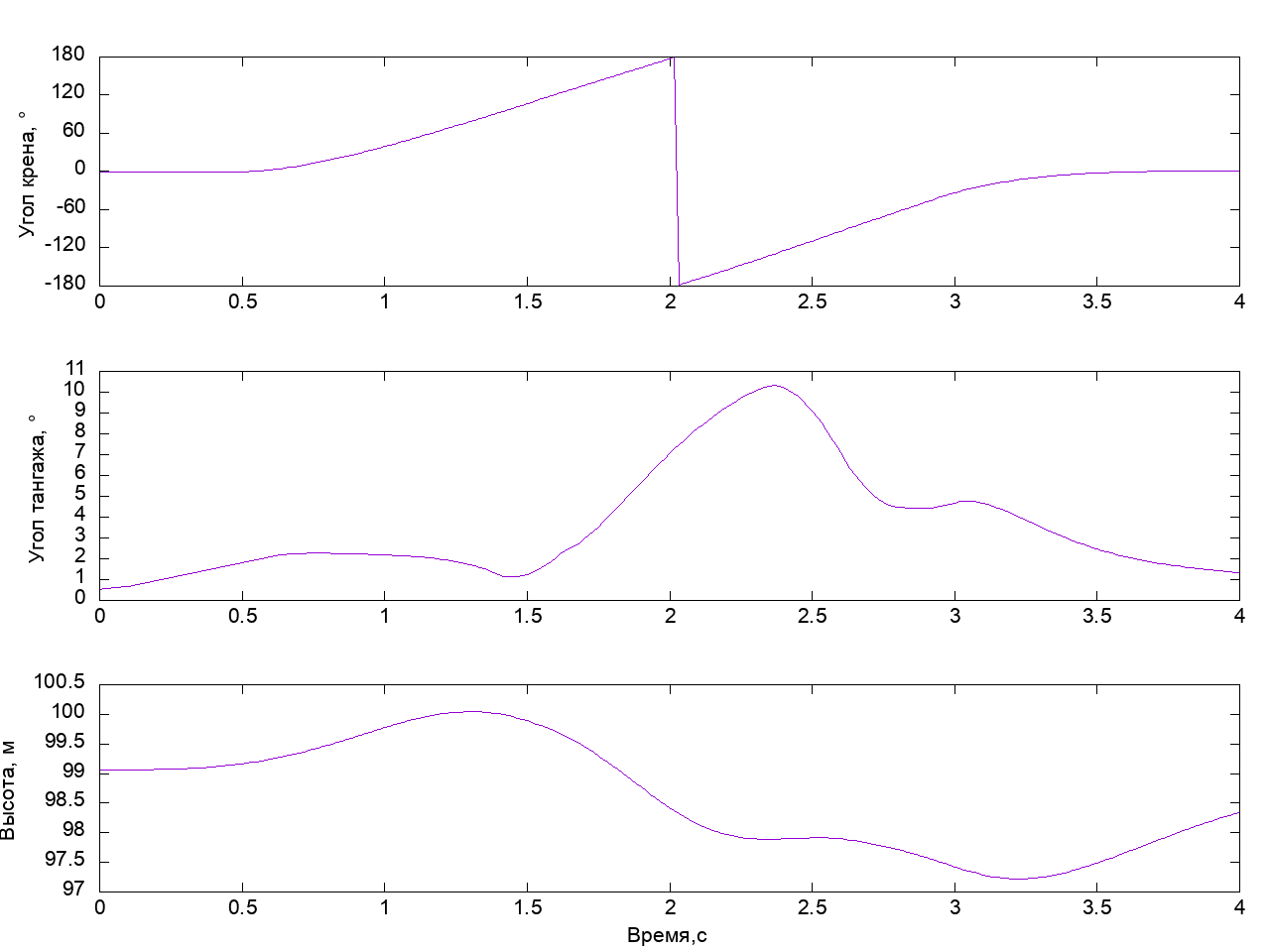
По крену аппарат повернулся на 180 градусов, при этом общий размах изменения высоты составил около 2.5 м — это в пять раз меньше, чем в предыдущем случае. Можно сказать, у нас получилась почти идеальная бочка.
Вместо заключения
Итак, мы рассмотрели некоторые принципы выполнения фигуры высшего пилотажа бочка и убедились, что, действуя разумно, мы можем на симуляторе выполнить неплохую по качеству бочку. Хорошо бы перейти к практике, и вот с помощью чего мы предполагаем это сделать — авиамодель + stm32f103 + mpu9250. Все эти элементы легко доступны и дешевы, так что любой желающий сможет попробовать сделать это сам. Результаты проб, ошибок и инструкция для повторения — тема следующих публикаций.
Источник


