![[Перевод] «Тетрис» в роли принтера [Перевод] «Тетрис» в роли принтера](https://habrastorage.org/webt/sa/az/2c/saaz2chpnuatbjn-rdg3zcryjwo.png)
Поворачивая, переставляя и опуская вниз заранее заданную последовательность фигур, Tetris Printer Algorithm использует механику «Тетриса» для генерации произвольных битовых изображений.
Описание алгоритма
Алгоритм построчно преобразует пиксели исходного изображения в квадраты поля «Тетриса», двигаясь снизу вверх. Для генерации отдельного квадрата алгоритм собирает структуру, состоящую из прямоугольной области, полностью опирающейся на один квадрат под ней. После завершения сборки прямоугольной области её строки очищаются, оставляя под собой один квадрат. Вот три примера такого поведения.



Как показано ниже, алгоритм также может генерировать одной структурой несколько квадратов.

В процессе построения строки все квадраты, созданные данным способом, должны на что-то опираться. На показанных выше изображениях сгенерированные квадраты стоят на полу игрового поля. Однако если произвольная строка содержит дырки, то она не сможет обеспечить опору, необходимую для построения строки над ней. Алгоритм решает эту проблему, создавая поверх строки с дырками плоскую платформу. В показанной ниже анимации построенная поверх строки платформа состоит из одного красного квадрата. Платформа — это временная структура, и вставка последней фигуры удаляет её.

Показанная ниже строка из 5 красных квадратов расположена поверх строки из 3 красных квадратов. Это реализовано построением плоской платформы поверх нижней строки. Платформа обеспечивает опору, необходимую для генерации 5 красных квадратов. В конце платформа удаляется при помощи вставки последней фигуры, а новая строка попадает на своё место. Заметьте, что если алгоритму нужно генерировать строки в обратном порядке (строка из 3 красных квадратов над строкой из 5 красных квадратов), то платформа будет не нужна.

Паттерны создания одного квадрата
Для справки приведу названия 7 тетрамино (игровых фигур).
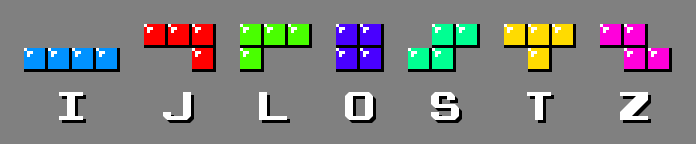
Представленная в статье версия Tetris Printer Algorithm разработана специально для рендеринга спрайтов из старых видеоигр. Эти игры упаковывали графику в тайлы 8×8, а на каждый пиксель выделялось 2 байта. Следовательно спрайты обычно содержали только 3 цвета плюс прозрачные области и чаще всего имели размер 16×16 или 16×32 пикселя.
В анимации ниже показаны все паттерны, используемые для создания отдельных квадратов. В каждом паттерне применяются взаимозаменяемые тетрамино J, T и L, создающие единственный квадрат внизу. Алгоритм назначает этим тетрамино один из 3 цветов, присутствующих в спрайте. Остальным тетрамино присваиваются произвольные цвета. На протяжении игрового процесса все цвета остаются постоянными.

Из-за формы трёх тетрамино невозможно создать квадрат из всех трёх цветов в первых двух и последних двух столбцах. Следовательно минимальная ширина игрового поля для рендеринга спрайта шириной 16 пикселей составляет 2 + 16 + 2 = 20 квадратов. Однако выяснилось, что 20 — это слишком мало.
Как показано ниже, область над единственным нижним квадратом не может состоять только из одной строки, потому что единственные фигуры, которые в него могут поместиться (тетрамино I), не имеют опоры.

При двух строках единственный способ растягивания целого игрового поля таким образом, чтобы оно имело опору — использование тетрамино S и Z. Но в таком случае в верхней строке будут оставаться дырки.
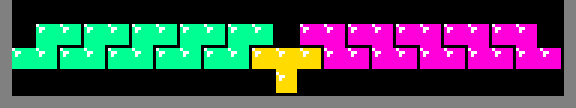
Минимальное количество строк, необходимых над нижним квадратом, равно 3, и как несколько раз показывалось выше, такие паттерны существуют. 20 квадратов — это минимальная ширина, необходимая для размещения спрайта шириной 16 пикселей. Но 20 × 3 + 1 = 61, а это число не делится на 4, а значит, не может быть построено из тетрамино. Однако ширина 21 даёт нам 21 × 3 + 1 = 64, и его можно построить из 16 тетрамино. На самом деле такая ширина позволяет алгоритму рендерить спрайты шириной до 17 пикселей.
Игровое поле оригинального «Тетриса» имеет размер 10×20 квадратов (соотношение 1:2). В данной версии алгоритма сохраняется это соотношение — игровое поле имеет размер 21×42 квадратов.
Так как тетрамино J, T и L взаимозаменяемы при создании одного квадрата, а 3 квадрата из этих тетрамино участвуют в создании строки над ним, существует 21 − 3 = 18 паттернов создания единственного квадрата. Однако из-за зеркальной симметрии, на самом деле их только 9. Очистка 3 строк срабатывает для большинства из этих 9. Однако тщательное компьютерное исследование показало, что двум паттернам нужно больше. Следующий возможный вариант — это 7 строк, потому что 21 × 7 + 1 = 148, для чего требуется 37 тетрамино. Как показано на изображениях ниже, такие паттерны существуют.


Паттерны создания нескольких квадратов
Паттерны создания нескольких квадратов ограничены теми же тремя цветами, создаваемыми паттернами единственного квадрата. Получаемые квадраты создаются из тетрамино J, T и L, каждое из которых занимает 3 квадрата в строке над строкой создания. Максимальное количество квадратов, которое потенциально можно создать одним паттерном, равно 21 / 3 = 7. Однако для спрайтов с шириной 16 пикселей самое правое тетрамино не может создать квадрат. Даже в случае спрайтов шириной 17 пикселей оно сможет создать квадрат только одного цвета. Поэтому паттерн создания из 7 квадратов используется редко.

Количество паттернов создания произвольного количества квадратов можно определить при помощи комбинаторики перечислений. Рассмотрим показанный ниже паттерн, представляющий строку над создаваемой из трёх квадратов строки. Каждый блок из трёх смежных белых квадратов обозначает часть тетрамино; создаваемые квадраты не показаны.

Три тетрамино создают 4 пустоты. Существует 21 − 3 × 3 = 12 тёмных квадратов, которые можно произвольно вставить в эти пустоты для образования конкретного паттерна. Количество способов распределения этих тёмных квадратов можно подсчитать, помещая их в строку, в которой единичные белые квадраты рассматриваются как разделители.

Итак, задача свелась к вычислению значения коэффициента многочлена. Взглянув на эти белые квадраты, можно понять, что это вопрос количества способов выбора 3 из 15. 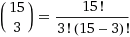 = 455.
= 455.
В общем случае, при n оно равно 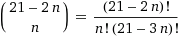 . Но из-за зеркальной симметрии на самом деле их оно вдвое меньше; если количество нечётно, то разделив на два, мы округляем до ближайшего целого, чтобы включить в него идеально симметричный паттерн, который должен существовать в этом множестве, как, например, показанный ниже для случая с 455.
. Но из-за зеркальной симметрии на самом деле их оно вдвое меньше; если количество нечётно, то разделив на два, мы округляем до ближайшего целого, чтобы включить в него идеально симметричный паттерн, который должен существовать в этом множестве, как, например, показанный ниже для случая с 455.

Применив эту формулу к 7 тетрамино, мы подтвердим очевидное: существует только один паттерн создания 7 квадратов.
Паттерн создания 6 квадратов можно построить двумя способами: двумя заполненными строками (2 × 21 + 6 = 48) и шестью заполненными строками (6 × 21 + 6 = 132), для чего требуются 12 и 33 тетрамино. Приведённая выше формула показывает, что существует 84 паттернов создания 6 квадратов, но только 35 из них можно построить из 2 полных строк. Для 49 паттернов требуется 6 строк. Числа нечётные из-за симметричных паттернов, которые показаны ниже.


Стоит также заметить, что здесь возможны 2 строки, потому что в отличие от паттерна создания одного квадрата, требовавшего тетрамино S и Z, в этих паттернах используются 6 фигур.
В таблице ниже показано количество создаваемых каждым типом паттернов квадратов, количество полных строк, количество используемых тетрамино и количество паттернов.
| Создаваемые квадраты | Полные строки | Тетрамино | Паттерны |
|---|---|---|---|
| 1 | 7 и 3 | 37 и 16 | 19 (4 и 15) |
| 2 | 6 | 32 | 136 |
| 3 | 5 | 27 | 455 |
| 4 | 4 | 22 | 715 |
| 5 | 3 | 17 | 462 |
| 6 | 2 и 6 | 12 и 33 | 84 (35 и 49) |
| 7 | 1 | 7 | 1 |
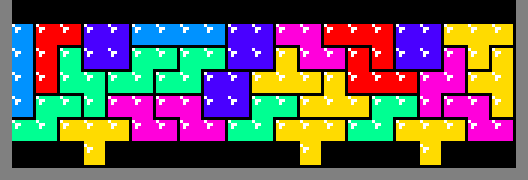
Примеры паттернов.



Платформы
Перед построением строки алгоритм исследует строку под ней. Если нижняя строка не может обеспечить опору для всех располагаемых над нею квадратов, то необходима временная платформа. Когда платформа удаляется, новая строка опускается вниз, и из-за того, как реализована гравитация в оригинальном «Тетрисе», некоторые квадраты остаются висеть в воздухе.
На иллюстрации ниже показаны 10 паттернов платформ. Построение платформы начинается с опускания тетрамино T поверх одного из квадратов последней сгенерированной строки. Остальные тетрамино опираются на эту первую T. То есть, если предыдущая сгенерированная строка содержиn как минимум 1 квадрат, как например красный квадрат на изображении ниже, мы можем создать над ним плоскую платформу для генерации следующей строки.

Посередине построения платформы нижняя строка завершается и удаляется, оставляя над собой три строки. Последняя тетрамино J или L, которая удалит эти строки, не вставляется, пока паттерны создания не сгенерируют следующую строку спрайта поверх платформы. Эта последняя фигура предотвращает создание квадратов в первых и последних двух строках. Но, как сказано выше, из-за геометрии используемых в этом процессе тетрамино J, T и L, паттерны создания квадратов ограничены 17 внутренними столбцами.
Кроме того, из 19 возможных способов построения платформ поверх тетрамино T, существуют только 10 показанных выше.
Упакованные матрицы
Как сказано выше, одно подмножество паттернов создания 6 квадратов включает очистку только двух строк. Все остальные паттерны требуют 6 строк. Чтобы понять, почему это так, рассмотрим показанный ниже паттерн.

Эти тетрамино взаимозаменяемы с тетрамино J и L, и каждое из них добавляет в общую строку 3 смежных квадрата. Строки, которые нужно завершить, представлены показанной ниже матрицей.
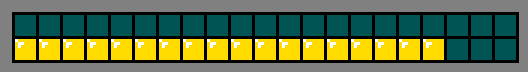
Теперь всё дело заключается в упаковке пустого пространства при помощи тетрамино. Начиная слева, единственный вариант — использовать последовательность тетрамино I.

Единственный способ заполнения оставшегося места — использовать J и O или I и L. Оба варианта показаны ниже.


К сожалению, в показанных выше матрицах тетрамино O и L не имеют опоры. Для этого паттерна создания 6 квадратов требуется матрица побольше.
Похожая проблема возникает у двух паттернов создания одного квадрата. Рассмотрим показанную ниже матрицу:

Единственный способ заполнения нижней строки справа — цепочка последовательности Z.

Аналогичным образом, единственный способ получения 3 пустых квадратов слева внизу требует тетрамино S.

В средней строке есть пустой квадрат между S и Z и единственный способ заполнить его — использовать тетрамино J, T или L, как показано на рисунках ниже.



Вставка любой из этих фигур разделяет пустое пространство. Пустая область слева содержит соответственно 5, 6 и 7 пустот. Так как ни одно из этих значений не делится на 4, продолжать невозможно. Для этого паттерна создания одного квадрата требуется матрица побольше.
То же самое относится к другому паттерну создания одного квадрата, показанного в матрице внизу.

После использования тетрамино S и Z для заполнения большей части нижней строки между ними остаётся пустое пространство в средней строке.

Как показано на изображениях ниже, вставка дыр разделяет пустое пространство, и пустая область слева содержит соответственно 9, 10 или 11 квадратов; ни одно из чисел не делится на 4.



Но упаковка матриц — не единственный способ генерации паттерна создания квадратов. Например, взгляните на показанный ниже создатель 4 квадратов.

Ниже показана попытка рендеринга паттерна как множества упакованных тетрамино.

Последняя L пропущена, потому что пространство для неё образуется только после завершения и удаления третьей строки.
Но после тщательного поиска было обнаружено, что эта техника не обеспечивает вышеупомянутым паттернам одного квадрата возможности работать только с 3 строками. Кроме того, не позволяет она и реализовать никаких новых паттернов 6 квадратов в двух строках. Нет никакой необходимости искать оставшиеся паттерны за пределами упакованных матриц, потому что они уже используют наименьшее возможное количество тетрамино. И ограничившись упакованными матрицами, мы гораздо быстрее найдём все необходимые паттерны.
Поиск паттернов
Чтобы упростить вывод данных, Tetris Printer Algorithm ограничивается созданием тетрамино в верхней центральной точке игрового поля, их поворотом, перемещением по горизонтали и опусканием. Ему никогда не приходится сдвигать фигуру по горизонтали после прохождения какого-то расстояния. Это ограничение сильно уменьшает пространство поиска, потому что не позволяет образовывать зазоры под добавляемыми в матрицу фигурами. Для примера давайте рассмотрим следующую матрицу создания 3 квадратов.

Если бросить J в центр матрицы, как показано выше, то мы получим зазор из 2 пустых квадратов, которые невозможно будет заполнить последующими фигурами. Следовательно, поиск не будет следовать по этому пути.

Так как накрытые зазоры не допускаются, каждый столбец в матрице можно рассматривать как стопку заполненных квадратов и высота этих стопок полностью описывает содержимое всей матрицы. Вне зависимости от количества строк, для описания двухмерной матрицы будет достаточно одномерного целочисленного массива с 21 элементом.
При падении фигуры в матрицу увеличиваются высоты стопок соответствующих столбцов. Для ускорения этого процесса все тетрамино анализируются заранее. Существует 19 поворотов тетрамино, и поиск считает каждый из них уникальной фигурой.
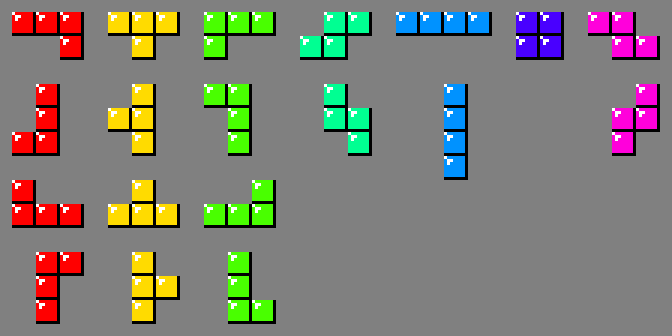
Тетрамино J в верхнем левом углу изображения занимает 3 столбца. При опускании на матрицу высоты 3 смежных стопок увеличиваются соответственно на 1, 1 и 2 квадрата. Но перед тем, как можно будет опустить фигуру, нижний профиль фигуры должен соответствовать верхнему профилю соответствующих стопок. Если бы эта J лежала на полу игрового поля, под каждым из этих столбцов должны были существовать зазоры в 1, 1 и 0 пустых квадратов. Так как зазоры запрещены, относительные высоты 3 стопок должны будут полностью соответствовать паттерну.
Ещё одним последствием отсутствия зазоров стало то, что при падении фигур в матрицу строки заполняются снизу вверх. Невозможно заполнить строку в середине матрицы, ранее или одновременно не завершив все строки под ней. В процессе заполнения матрицы её нижняя граница фактически продвигается наверх. Следовательно, стопка столбца матрицы способна обеспечить опору, только если её высота минус количество завершённых строк больше 0. Когда в матрицу добавляется фигура, по крайней мере один из соответствующих столбцов должен обеспечить опору.
Поиск хранит второй одномерный массив, содержащий количество заполненных квадратов в каждой строке. Вышеупомянутая J содержит в соответствующих строках 3 и 1 квадрат. При вставке её в матрицу эти значения прибавляются к соответствующим элементам массива. Количество завершённых строк — это количество элементов со значением 21.
Как сказано в предыдущем разделе, если добавленная фигура разделяет матрицу, то размеры получающихся областей должны делиться на 4. Например, на изображении ниже прибавление I создаёт 2 области, в каждой из которых содержится 46 пустых квадратов. Так как 46 не делится на 4, больше нет никакой возможности заполнения остатка матрицы.
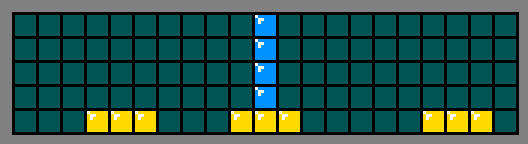
Разделение появляется, когда высота стопки равна высоте матрицы. После вставки фигуры инкрементом высот соответствующих стопок размеры всех разделённых областей пустого пространства можно определить сканированием массива высот и сложением оставшегося в каждой стопке пространства. Это число проверяется и сбрасывается при обнаружении разделения.
Поиск, используемый для генерации всех паттернов, применяет рандомизированное инкрементное построение (randomized incremental construction) — алгоритм с возвратом назад, систематически проверяющий все комбинации в случайном порядке. Инкрементное построение решения случайной вставкой фигур заставляет его расти подобно кристаллу. Случайность обеспечивает неравномерность, содержащую ломаные грани, служащие основанием для последующих добавляемых фигур. БОльшая часть матрицы очень быстро упаковывается случайным образом, а когда пустое пространство становится дефицитным, в дело вступает возврат назад (backtracking).
Перед выполнением поиска совершаются случайные перестановки 371 способов добавления фигуры в матрицу. Ниже показан псевдокод функции поиска.
private Result search(Matrix matrix, int remaining) {
if (remaining == 0) {
return SOLUTION
}
attempts := attempts + 1
if (attempts >= MAX_ATTEMPTS) {
return TIMEOUT
}
if (внизу матрицы есть место для S или Z) {
попытаться случайным образом добавить в это пространство S или Z
if (фигура вставлена успешно) {
Result result := search(matrix, remaining - 1)
if (result == SOLUTION) {
return SOLUTION
}
удалить последнюю добавленную фигуру из матрицы
if (result == TIMEOUT) {
return TIMEOUT
}
}
}
случайным образом выбираем перестановку способов вставки фигуры в матрицу
for(каждого способа вставки фигуры, упорядоченного по выбранной перестановке) {
попытаться добавить фигуру в матрицу
if (фигура была вставлена успешно) {
Result result := search(matrix, remaining - 1)
if (result == SOLUTION) {
return SOLUTION
}
удалить последнюю добавленную фигуру из матрицы
if (result == TIMEOUT) {
return TIMEOUT
}
}
}
return NO_SOLUTION
}
Исходная матрица, передаваемая функции поиска, пуста, за исключением нижней строки, содержащей блоки из 3 соседних квадратов. Она передаётся вместе с количеством оставшихся фигур, которые нужно добавить. Если remaining равно 0, то матрица содержит решение и функция выполняет возврат. Каждый рекурсивный вызов совершает инкремент глобального количества попыток attempts. Если оно превышает MAX_ATTEMPTS, имеющее значение 1000, то поиск начинается заново.
Третий оператор if пытается добавить в низ матрицы тетрамино S или Z, если это позволяет пространство. Смысл этого заключается в том, чтобы избегать ситуаций наподобие показанной ниже, когда алгоритм тратит время на заполнение части матрицы, не имея возможности заполнить остальное из-за нехватки опоры.

Благодаря оператору if он быстро образует платформу, на которой можно выполнять строительство:

Для выполнения попытки добавления в матрицу фигуры требуются описанные выше проверки. Алгоритм проверяет, будет ли фигура иметь опору, учитывая завершённые строки. Также он проверяет, делится ли на 4 размер каждого отдельного пустого пространства, создаваемого вставкой фигуры.
Преобразование изображений
Tetris Printer Algorithm преобразует каждую строку битового изображения в последовательность проходов. Двигаясь слева направо, каждый проход «жадным» образом вставляет тетрамино J, T и L туда, куда они помещаются. Например, на изображении ниже показана строка из 16 пикселей битового изображения.

На изображении ниже показаны 5 проходов, требуемые для покрытия этих 16 пикселей.





Последовательность фигур, которые алгоритм пытается вставить, определяется цветами пикселей. Чтобы фигуры не накладывались друг на друга, используется одномерный массив булевых значений. Для вставки фигуры в массиве должны присутствовать 3 нулевых элемента. При успешной вставке фигуры 3 соответствующих элемента массива принимают значение 1.
Для отслеживания завершённых пикселей между несколькими проходами используется второй одномерный массив булевых значений. Когда каждый элемент равен 1, строка завершена.
В конце каждого прохода преобразователь изображений выполняет поиск в таблице всех паттернов создания одного и нескольких квадратов. На выход он передаёт соответствующий паттерн со вставленными внизу тетрамино J, T и L. Например показанный выше первый проход выводится как следующий паттерн создания 5 квадратов:

Поиск в реальном времени
Описанный в предыдущем разделе преобразователь изображений чрезвычайно быстр, потому что использует постоянную таблицу, содержащую все паттерны создания квадратов, а не выполняет их поиск в реальном времени. Однако поиск в реальном времени может воспользоваться паттернами, отсутствующими в таблице, а следовательно, сильно снизить количество тетрамино, необходимых для генерации изображения. Он пользуется квадратами, созданными в предыдущих проходах, применяя их в качестве дополнительных опор. Например, как говорилось выше, следующий паттерн создания одного квадрата требует 7 полных строк.

Но один красный квадрат, созданный в предыдущем проходе в левом нижнем углу на изображении ниже обеспечивает дополнительную опору, снижающую количество заполненных строк до 3.

Кроме того, поиск в реальном времени может покрыть 3 смежных пикселя одного цвета, перевернув тетрамино J, T или L.

На самом деле, он может комбинировать перевёрнутые и неперевёрнутые тетрамино, покрывая за один проход большое количество пикселей. Например, показанные выше 5 проходов, необходимых для покрытия 16 пикселей, можно свести к показанному ниже одному проходу.

Для получения этого паттерна преобразователь изображений начинает с жадной упаковки перевёрнутых тетрамино J, T и L.

Затем он жадно пытается добавить неперевёрнутые версии, и в данном случае ему удаётся добавить ещё одну J.

В принципе, в этом процессе можно также использовать предварительно вычисленную таблицу поиска, но огромный размер такой таблицы делает её неприменимой на практике.
В этом примере 8 квадратов в строке над создаваемой строкой добавляются в нижнюю строку пустой матрицы. Для n квадратов на игровом поле шириной 21 квадратов высота матрицы h — это наименьшее положительное целое число, такое, что 21h − n делится на 4. В данном случае требуется матрица высотой 4.

Поиск в реальном времени действует точно так же, как и описанный выше алгоритм поиска, но имеет незначительные усовершенствования. Как и раньше, стопка столбца матрицы обеспечивает опору, только если высота стопки минус количество завершённых строк больше нуля. Когда разность равна нулю, стопка столбца не должна обеспечивать опоры. Однако в этой версии при равенстве нулю она проверяет квадраты в создаваемой строке, сгенерированные предыдущими проходами. То есть любые квадраты в строке под нижней строкой матрицы обеспечивают опору для пустых столбцов.
Кроме того, поскольку поиск выполняется в реальном времени, непрактично будет делать его исчерпывающим. Если он не обнаружил решение после заданного количества попыток, то он добавляет ещё 4 строки сверху матрицы, а потом пробует снова. После этого, если он по-прежнему не нашёл решение после заданного количества попыток, то в текущем проходе возвращается к методике с заранее вычисленными таблицами поиска и преобразованием изображений, описанной в предыдущем разделе статьи.
Печать
Для печати необходимо выполнять на игровом поле «Тетриса» инструкции, выводимые преобразователем изображений. Принтер создаёт определённое тетрамино в верхней центральной точке игрового поля в стандартной ориентации. Затем принтер поворачивает его, сдвигает по горизонтали и опускает. Этот процесс показан в видео:
Исходный код
Исходный код проекта на Java 7 выложен здесь.
Алгоритмы поиска по заранее подготовленным таблицам и реального времени находятся в пакетах search.precomputed и search.realtime. Они используют некоторые общие классы, расположенные в пакете search. Результаты заранее вычисленного поиска хранятся в пакете patterns в виде последовательности текстовых файлов. Текстовые файлы хранят упакованные матрицы в виде символов ASCII, начиная с A. Например, первые 3 матрицы в emitters1.txt (множестве паттернов создания одного квадрата) выглядят так:
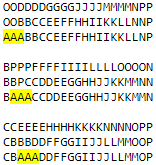
Как многократно говорилось в статье, 3 смежных символа A в показанных выше матрицах можно заменить тетрамино J, T или L. Символы B, C, D и так далее представляют последовательность тетрамино, которые нужно создать.
Класс imageconverter.ImageConverter содержит метод main, получающий единственный аргумент командной строки: название спрайтового файла изображения. Изображение не может быть больше 17×32 пикселей и не может содержать более 3 непрозрачных цветов. Все остальные пиксели должны быть прозрачными.
Интересно, что в старых видеоиграх для получения дополнительного цвета разработчики часто использовали фон. Например, зрачки и рот Буба из Bubble bobble, зрачки Донки Конга из Donkey Kong и бровь с родинкой мисс Пэкмен из Ms. Pac-Man на самом деле прозрачные. Чёрный цвет получается из фона со сплошной заливкой.

Фон игрового поля «Тетриса» можно использовать аналогичным образом.
Выходные данные ImageConverter выглядят подобно этому фрагменту:

3 hex-значения в первой строке — это 3 непрозрачных цвета, извлечённых из спрайтового файла изображения. Они соответствуют цветам тетрамино J, T и L. Цвета других тетрамино никак не влияют на изображение. Остальные блоки — это упакованные паттерны, выполняемые на игровом поле (символы после Z и до a см. в таблице ASCII-символов). Выделенные жёлтым блоки составляют платформу. Первый блок добавляет платформу, второй — удаляет её.
Класс printer.Printer получает текстовый файл в этом формате и генерирует файл изображения, играя в «Тетрис».
Алгоритм принтера, использованный для генерации видео, напоминающего NES-версию «Тетриса», определяет каждый тип тетрамино в каждом блоке текстового файла. Затем он двигается в обратном порядке от начальной точки и исходной ориентации к углу поворота и координатам опускания фигуры, указанным в файле. Примечание: из-за чрезвычайно высокой скорости падения фигур, в реальной NES-версии «Тетриса» невозможно пройти дальше 30-го уровня. Предполагается, что принтер передаёт игровому полю все свои команды достаточно быстро. чтобы компенсировать это.
Для повторной генерации файлов паттернов воспользуйтесь search.precomputed.PatternSearcher. Его можно настраивать при помощи изменения констант в начале файла исходного кода.
public static final int MATRIX_WIDTH = 21;
public static final int MATRIX_HEIGHT = 4;
public static final int EMITTED_SQUARES = 4;
public static final int RANDOM_SETS = 100000;
public static final int MAX_ATTEMPTS = 1000;
RANDOM_SETS — это количество случайных перестановок 371 способа добавления фигуры в матрицу. При задании значения 100000 для инициализации перестановок при запуске требуется несколько секунд. Кроме того, для их хранения требуется более гигабайта памяти.
MAX_ATTEMPTS управляет временем выполнения поиска. Относительно небольшое значение 1000 позволяет поиску быстро отбрасывать случайные начала, которым не удаётся хорошо себя проявить. Однако чтобы доказать, что для конкретного размера матрицы и количества создаваемых квадратов нет решения необходимо целиком исследовать всё пространство поиска. Для этого можно присвоить MAX_ATTEMPTS значение Integer.MAX_VALUE.
Похожие константы встречаются в search.realtime.RealtimeSearcher, который используется преобразователем изображений. Как говорилось выше, большое значение RANDOM_SETS требует увеличения максимальной памяти и приводит к более долгому запуску. MAX_RETRIES управляет количеством попыток, после которого поиск в реальном времени сдаётся и возвращается к поиску с заранее вычисленной таблицей.
Учтите, что оба алгоритма поиска задействуют 100% ЦП, создавая множество параллельных потоков, равных по размеру доступному количеству процессоров.