[Перевод] Спросите Итана №106: где конкретно ошибся Ньютон?

Мы знаем, что общая теория относительности Эйнштейна заменила ньютоновскую теорию гравитации, но где именно ошибся Ньютон?

Для меня никогда не было более высокой чести или признания, чем те, что связаны с развитием науки.
— Исаак Ньютон

Каждую неделю вы присылаете мне ваши вопросы и предложения для еженедельной колонки «спросите Итана». Иногда это спекулятивные вопросы о будущем, иногда это вопросы о крупномасштабных структурах Вселенной или самых мелких частицах. Иногда это вопросы о космосе или границах нашего знания. На этой неделе меня заинтересовал вопрос Франсуа Зинсерлинга о дольше всех существовавшей физической теории и о её провале:

Эйнштейновская общая теория относительности стоит выше законов Ньютона. Это мы поняли. Что мне хотелось бы узнать: с подходом Ньютона получается несоответствие прецессии орбиты Меркурия. А что мы наблюдаем? Согласно Ньютону получается больше или меньше гравитации? Или проблема лежит где-то ещё?

Орбита каждой планеты в Солнечной системе проходит вокруг Солнца. Она представляет собой не идеальный круг, но эллипс, что Кеплер заметил почти за сто лет до Ньютона. Орбиты Венеры и Земли очень близки к круговым, а Марса и Меркурия – более эллиптические, их минимальное расстояние до Солнца сильно отличается от максимального.

Конкретно у Меркурия афелий (самая удалённая от Солнца точка) на 46% дальше, чем перигелий (самая ближайшая позиция к Солнцу). У Земли разница составляет всего 3,4%. Этот факт не имеет отношения к разным теориям гравитации; просто условия, в которых эти планеты сформировались, привели к таким свойствам их орбит.

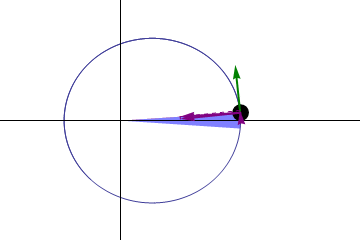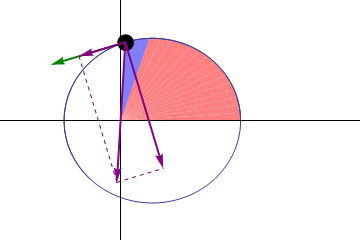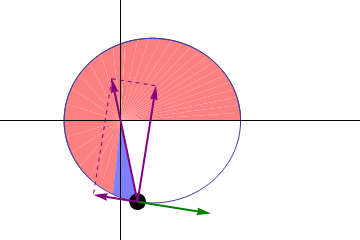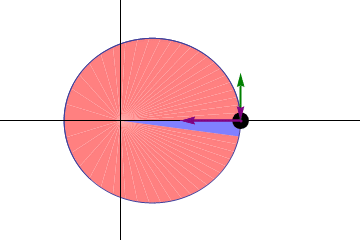
Но то, что эти орбиты отличаются от идеальных окружностей, означает, что из них можно узнать кое-что интересное. Если бы законы Кеплера были идеальны, тогда планета, вращающаяся вокруг Солнца, должна была возвращаться в одну и ту же точку после каждого оборота. Если мы в каком-либо году достигли перигелия, а затем отсчитали ровно год, мы тоже должны оказаться в перигелии, и можем ожидать от Земли, что она попадёт ровно в ту же точку пространства – относительно остальных звёзд и Солнца, что и в прошлом году.

Но законы Кеплера не могут быть идеальными, ибо они применимы к безмассовым телам, вращающимся вокруг массивного, в отсутствии остальных масс. Но эта ситуация вообще не описывает нашу Солнечную систему.

У нас есть куча массивных тел – планеты, луны, астероиды – кроме единственной планеты на орбите вокруг Солнца. Кроме того, сами по себе измеряемые планеты также обладают массой, поэтому они вращаются вокруг не центра Солнца, а общего центра масс системы планета/Солнце. И наконец, у Земли есть ещё одно неприятное свойство: прецессия оси, приводящая к наличию разницы между тем, как мы отмечаем год (тропический год, относящийся к сезонам и календарю) и возврат Земли на ту же позицию в космосе (звёздный год, относящийся к завершённой орбите).

И все эти особенности нужно принять во внимание, чтобы предсказывать изменения орбит других планет. Чего можно ожидать, получив все те знания, которые у нас есть, по Земле, Меркурию и всем остальным обнаруженным и измеренным нами массам?

К примеру, разница между звёздным и тропическим годами небольшая, но важная: звёздный год длиннее на 20 минут и 24 секунды. Это значит, что мы отмечаем сезоны, равноденствия и солнцестояния на годовом календаре, но наш перигелий относительно него постепенно сдвигается. Если круг состоит из 360°, то с 1 января одного года до 1 января следующего мы проходим всего лишь 359,98604°, а это значит, что перигелий каждой планеты сдвигается на 5025″ каждое столетие (в одном градусе 60′, угловых минут, а в одной минуте – 60″, угловых секунд). И этот сдвиг выглядит как продвижение по орбите вперёд.

Но необходимо учитывать ещё и планетарные массы.

Каждая планета влияет на движение другой планеты по-разному, в зависимости от расстояния между ними, их масс и близости орбит, а также от того, какая орбита находится внутри какой. Для Меркурия, самой внутренней из планет, расчёты проводить легче всего: все остальные планеты для него будут внешними, и поэтому все они приводят к продвижению перигелия вперёд. Вот результаты влияния этих планет, в порядке убывания важности:
• Венера: 277,9″ за столетие.
• Юпитер: 153,6″ за столетие.
• Земля: 90,0″ за столетие.
• Сатурн: 7,3″ за столетие.
• Марс: 2,5″ за столетие.
• Уран: 0,14″ за столетие.
• Нептун: 0,04″ за столетие.

Другие эффекты, включающие наличие массы у самого Меркурия, движение Солнца относительно центра масс Солнечной системы, вклад астероидов и объектов из пояса Койпера, несферичность Солнца и планет, вносят вклад, не превышающий 0,01″ за столетие, который можно проигнорировать.

Все эти эффекты вносят вклад в 523″ за столетие, и в сумме мы получаем 5557″ за столетие, добавив прецессию земной оси. Но если мы посмотрим на измерения того, что происходит на самом деле, мы получим продвижение перигелия на 5600″ за столетие. Это было известно уже в конце XIX века благодаря невероятным наблюдениям Тихо Браге, берущим своё начало аж в XVI веке! Такие небольшие отклонения можно увидеть, если вести наблюдения в течение 300 лет.

Прецессия превосходит предсказания Ньютона; вопрос в том, почему. Существует несколько намёков на ответ, если вы знаете, где их искать.

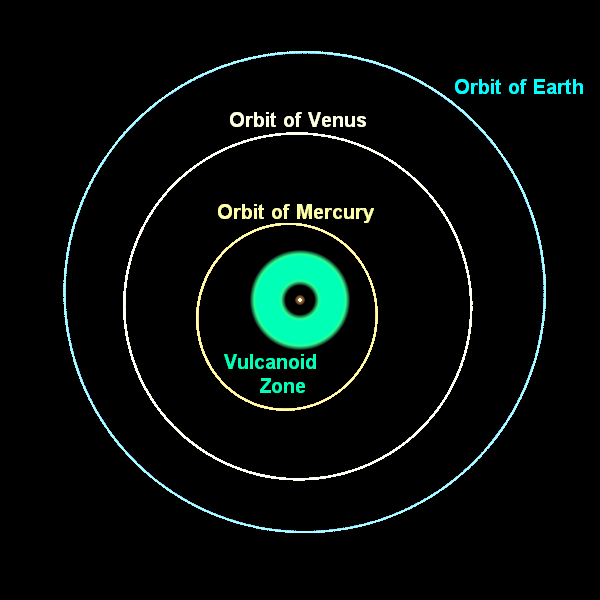
Сначала было решено, что внутри орбиты Меркурия есть ещё одна планета, и её характеристики приводят к такому эффекту – или же что солнечная корона очень массивная. Но корона Солнца оказалась не массивной, и никакой планеты Вулкан (а мы её искали) не существует – так что эти версии вычеркнули.

Вторую идею высказали двое учёных, Саймон Ньюкомб и Асаф Холл [Simon Newcomb and Asaph Hall], определившие, что если заменить закон обратных квадратов Ньютона, утверждающий, что гравитация с расстоянием убывает пропорционально его квадрату, на другой закон со степенью в 2,0000001612, то эта прецессия укладывается в подсчёты. Сегодня мы знаем, что такое предположение не соответствовало бы наблюдаемым орбитам Луны, Венеры, Земли – так что это тоже вычеркнули.

Третий намёк сделал Анри Пуанкаре, отметив, что если принять СТО Эйнштейна – учитывая, что Меркурий двигается вокруг Солнца со скоростью в 48 км/с, или с 0,016% скорости света – можно найти часть потерянной прецессии (но не всю её целиком).

Сочетание второй и третьей идей привело к общей теории относительности. Идею существования ткани пространства времени высказал один из бывших учителей Эйнштейна, Герман Минковский, и применение Пуанкаре этой концепции к задаче орбиты Меркурия стало важным шагом к нахождению решения. А идея Ньюкомба-Холла, пусть и неверная, показала, что если бы гравитация действительно была бы сильнее, чем её предсказывал Ньютон, это привело бы к недостающей прецессии.

Идея Эйнштейна была в том, что присутствие вещества/энергии приводит к искривлению пространства, и что чем ближе ты к более массивному объекту, тем сильнее ведёт себя гравитация. Кроме того, тем сильнее проявляются отклонения от ньютоновской гравитации.

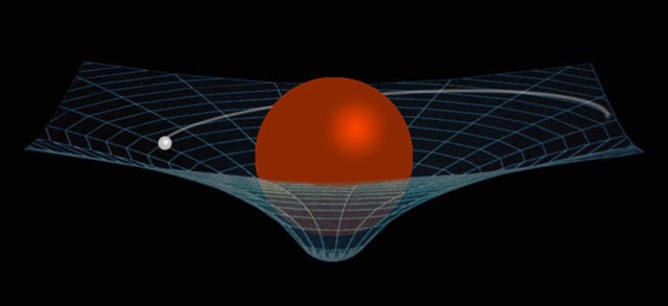
И вот он, ответ на вопрос Франсуа – но это ещё не конец истории. Когда Эйнштейн разработал свою теорию достаточно для того, чтобы предсказать дополнительную прецессию, результат его расчётов – дополнительные 43″ за столетие – сначала был признан чрезмерным. В то время ньютоновский вклад был неверно подсчитан и оценивался всего в 38″ за столетие. Этот аргумент использовали для оспаривания ОТО.

Для проверки того, какая из теорий верна, потребовалось предсказание искривления света, проходящего мимо массивного тела.

Теория Ньютона предсказывала, что звёздный свет вообще не отклоняется, проходя мимо Солнца, ибо он не имеет массы. Но если присвоить свету массу на основе эйнштейновского E=mc², или m=E/c², можно найти, что свет должен отклоняться на 0,87″ при проходе мимо внешнего края Солнца. А эйнштейновская теория предсказывала вдвое большее отклонение: 1,75″.

Цифры были невелики, но совместная экспедиция Артура Эддингтона и Эндрю Кроммелина [Arthur Eddington and Andrew Crommelin] во время затмения солнца 1919 года смогла провести измерения с нужной точностью. Они получили отклонение в 1,61″ ± 0,30″, что в пределах погрешности совпадало с эйнштейновскими предсказаниями, а не с ньютоновскими. Теория гравитации Ньютона провалилась.

Вот и вся история того, как заменили ньютоновскую гравитацию, и почему. С тех пор у ОТО было много побед (и никаких поражений), но во всех случаях, когда ньютоновская и эйнштейновская теории отличаются, победителем – с более сильными гравитационными эффектами вблизи массивных тел – выходит Эйнштейн. Наука шагает вперёд, но иногда шаги занимают очень много времени!