[Перевод] Специалисты по информатике идут нехожеными дорогами

Спустя десятилетия застоя, найдены новые короткие пути для задачи коммивояжёра

Не так давно команда исследователей из Стэнфорда и Университета Макгилла побили 35-летний рекорд по информатике на невообразимо малую величину – на четыре сотых триллионной триллионной триллионной доли процента. Прорыв – сделанный в классической для информатики задаче коммивояжёра – был слишком малым для какого бы то ни было практического значения, но он вдохнул новую жизнь в поиски улучшенных приближённых решений.

Задача формируется так: для набора городов, соединённых дорогами, необходимо найти кратчайший путь посещения каждого города с возвратом в точку старта. У решений задачи есть практические применения от сверления отверстий в печатных платах до управления расписанием задач на компьютере и упорядочивания свойств генома.

Задачу коммивояжёра легко сформулировать, и – в теории – легко решить, проверив все возможные замкнутые пути для поиска кратчайшего. Проблема с подходом грубой силы в том, что при росте количества городов соответствующее количество путей очень быстро начинает превышать возможности самых быстрых компьютеров. Для десяти городов существуют более 300 000 путей. Для 15 городов их количество возрастает до 87 миллиардов.

Алгоритм Кристофидеса

В раннюю компьютерную эру математики надеялись, что кто-нибудь найдёт удобный подход к задаче – некий алгоритм, позволяющий решать её за разумное время. Но хотя программисты достигли прогресса в конкретных случаях – определении кратчайшего пути для 49 городов в 1950-х, для 2392 городов в 1980-х и для 85900 городов в 2006 – никто не предложил алгоритм, эффективно решающий задачу в общем случае. Согласно примечательной работе 1972 года, возможно, что такого алгоритма вообще не существует. Специалист по информатике Ричард Карп из Калифорнийского университета в Беркли, показал, что задача коммивояжёра NP-полная, что означает, что эффективного алгоритма не существует (если только никто не докажет, что P = NP – но большинство учёных считают, что это не так).

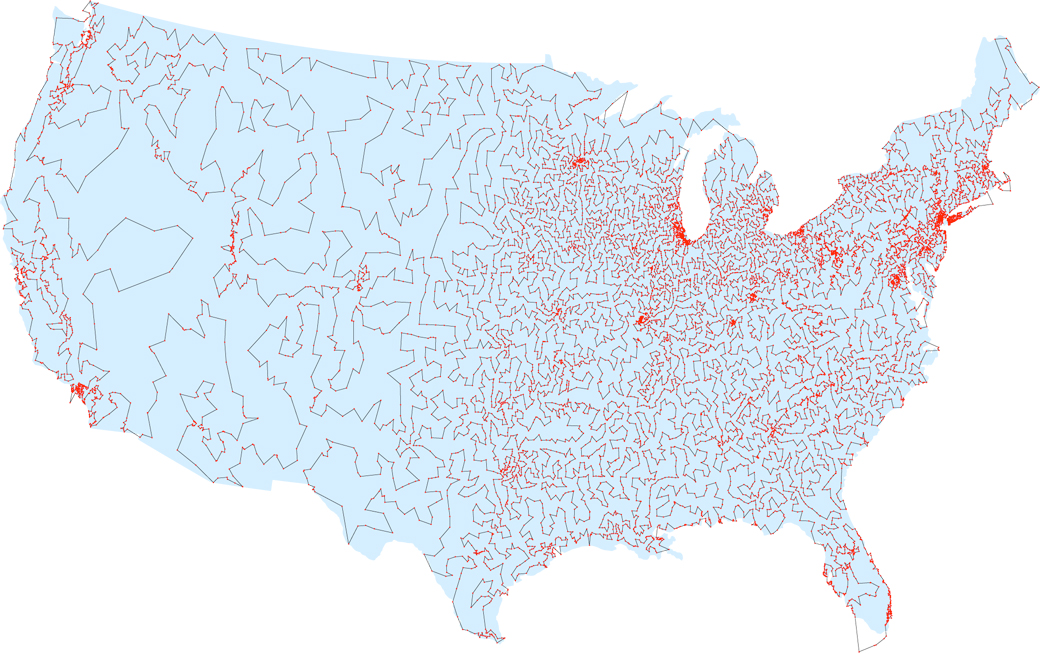
Самый короткий путь через все 13 509 городов США, население которых превышает 500 человек (по данным 1998 года)

После публикации работы Карпа многие специалисты по информатике занялись разработкой эффективного алгоритма поиска приблизительных решений задачи – замкнутых путей, чья длина ненамного превышает длину самого короткого. И здесь им повезло больше – в 1976 Никос Кристофидес, профессор в Имперском колледже Лондона, разработал алгоритм, выдающий пути, гарантированно не превышающие кратчайший путь более чем на 50%.

После его создания многие учёные решили, что этот алгоритм, достаточно простой для изучения студентами за час, станет промежуточным звеном, после которого будет найден более сложный, лучше аппроксимирующий истинное решение. Но десятилетия спустя таких алгоритмов так и не появилось.

«Почти все студенты, изучающие информатику, проводили недели или месяцы в попытках улучшить алгоритм Кристофидеса», говорит Санджеев Арора [Sanjeev Arora], учёный из Принстонского университета.

Наконец, в 2011 году команда Стэнфорда и Макгилла продвинулась за пределы 50% гарантии для определённых типов задач коммивояжёра и показала, что их решения будут превышать самый короткий путь не больше, чем на 49.99999999999999999999999999999999999999999999999996%.

С тех пор появился ряд улучшенных приближённых алгоритмов, благодаря свежему взгляду на задачу. И хотя эти приближения применимы лишь к определённым типам задач коммивояжёра, их подход довольно многообещающий, по словам Майкла Гоманса [Michel Goemans], специалиста по информатике из Массачусетского технологического института.

«Мы лишь слегка коснулись поверхности,- говорит он. – Я верю в то, что, может, лет через пять, мы достигнем более впечатляющих результатов».

Кратчайшее дерево

Мона Лиза как путь между 100 000 городами

Алгоритм Кристофидеса начинает не с поисков кратчайшего пути, а с поисков минимального остовного дерева – набора соединяющих города ветвей без замкнутых петель. В отличие от кратчайшего пути, минимальное остовное дерево довольно легко построить – нужно начать с поиска кратчайшего пути между двумя городами; это будет первая ветвь. Чтобы добавить следующую, нужно найти кратчайший путь между новым городом и одним из двух предыдущих – и так далее, пока не будут охвачены все города.

Результирующее дерево – это не одно из возможных решений задачи коммивояжёра, поскольку оно не даёт нам замкнутого пути. Но его можно превратить в такой путь, представив, что ветви – это стены, а затем прогулявшись по дереву так, чтобы ваш палец касался стены, пока вы не придёте к началу. Результирующая прогулка проходит через каждый город и возвращается назад, но обычно она далеко отстоит от кратчайшего пути, поскольку много раз проходит по одним и тем же отрезкам – каждую стену в дереве мы проходим дважды, по одному разу с каждой стороны.

Но полученный путь в худшем случае не длиннее кратчайшего пути вдвое. Добавив особым образом отбираемые ветви и применив несколько хитростей, Кристофидес показал, как урезать этот путь так, чтобы он не превышал кратчайший более чем на 50%.

Минимальное остовное дерево – естественная отправная точка для постройки короткого обходного пути. Но этот подход также стал отправным для исследователей, пытавшихся ужать 50%-ную гарантию Кристофидеса. Ведь хотя минимальное остовное дерево сначала выглядит эффективным, другие деревья могут подойти лучше для процесса преобразования деревьев в обходной путь – к примеру, к дереву без разветвлений нужно добавить лишь один отрезок пути, чтобы оно стало обходным путём.

Так что целью стал поиск дерева, соблюдающего баланс между длиной и простым преобразованием в обходной путь. Эффективных алгоритмов для поисков идеального дерева нет (если P=NP не истинно), но успешному приближённому алгоритму нужно найти только достаточно хорошее.

Дробное путешествие

Путь к «достаточно хорошему» дереву включал популярную, хотя и контринтуитивную, технику, признающую дробные решения для определённых задач. К примеру, дробный обходной путь может включать путешествие до половины пути между Миннеаполисом и Детройтом, и до половины пути между Кливлендом и Детройтом. С практической точки зрения такой путь не имеет смысла. Но его можно точно описать математически, и в отличие от классической задачи коммивояжёра, такую дробную версию можно решить эффективно.

Многие задачи аппроксимации в информатике можно решать, подсчитывая решения для дробной версии задачи, а затем по-умному округляя доли, чтобы получить примерное решение исходной задачи. Но до недавних пор никто ещё не придумал, как это можно сделать в случае задачи коммивояжёра.

В 2009 году Амин Сабери [Amin Saberi] из Стэнфордского университета и Араш Асадпур [Arash Asadpour], тогда ещё аспирант, разработали общую схему округления, использующую случайные числа для подбора целочисленного решения, сохраняющего как можно больше свойств дробного решения. Сабери считал, что эта схема напоминает «тяжёлый молоток в поисках гвоздя». И он подозревал, что подходящим гвоздём может оказаться задача коммивояжёра.

Через несколько месяцев Сабери, Асадпур, Гоманс, аспирант Стэнфорда Шайан Гаран [Shayan Gharan] и Александер Мадри [Aleksander Madry], ныне работающий в Федеральной политехнической школе Лозанны в Швейцарии, показал, что новая техника округления может дать хороший приближённый алгоритм для одного из вариантов задачи коммивояжёра, «асимметричного» случая. Через год Сабери, Гаран и Мохит Сингх [Mohit Singh] из Университета Макгилла использовали тот же подход для разработки нового приближённого алгоритма для обычной задачи коммивояжёра.

Крупнейшей решённой задачей коммивояжёра стал путь между 85 900 городами, подсчитанный в 2006 году. Расположение «городов» соответствует дизайну конкретного компьютерного чипа, созданного в лаборатории Белла, и решение является кратчайшим путём для лазера, его вырезающего

Получив карту городов и путей, новый алгоритм начинает с подсчёта точного дробного решения задачи коммивояжёра. Затем он округляет это решение до остовного дерева, которое теоретически должно близко подходить к балансу между длиной и простым преобразованием в обходной путь. Наконец, алгоритм включает это дерево – а не минимальное остовное дерево – в сеть Кристофидеса.

Новый алгоритм был «идеей, которую мы могли бы объяснить за пару часов, но её доказательство заняло около года», говорит Сабери.

После долгого анализа команда Стэнфорда/Макгилла смогли улучшить алгоритм Кристофидеса на небольшую долю для широкого подкласса задач коммивояжёра, «графических». Через несколько месяцев другие команды, вдохновлённые успехом, использовали другие схемы округления для получения алгоритмов для графического случая с лучшими приближениями. Текущий рекорд составляет 40%, что сильно лучше 50% Кристофидеса.

Графический случай «включает в себя много тех же трудностей, что встречаются и в общей проблеме», говорит Арора, добавляя, что схемы, работающие в графическом случае, могут пригодиться и для общей задачи коммивояжёра.

Тем не менее, говорит Сабери, решение общей приближённой задачи коммивояжёра, скорее всего, потребует новых идей. «Математическое открытие – как движение по тёмной комнате. Протягиваете руку и обнаруживаете стул, протягиваете руку и находите стол», говорит он, перефразируя математика Эндрю Уайлса. «В какой-то момент рука находит выключатель, и внезапно всё становится понятным. В случае задачи коммивояжёра даже после такого количества работ, нащупавших так много границ возможного, мне не кажется, что мы уже нашли этот выключатель».