![[Перевод] Интеллектуальный брутфорс: пишем головоломку и солвер для неё [Перевод] Интеллектуальный брутфорс: пишем головоломку и солвер для неё](https://habrastorage.org/webt/lr/rs/oi/lrrsoigqli7_jgtiwmzpbb21z_y.png)
Небольшое предисловие
В колледже я много играл в головоломки. В статье под головоломками я буду подразумевать очень узкое подмножество таких игр. Вот некоторые из примеров:
Также мне посчастливилось изучать структуры данных в Политехническом институте Ренсселера, где в то время студенты профессора Катлера (привет, Барб!) ежегодно участвовали в соревновании по написанию солвера головоломок. Каждый год игра менялась, и в мой год это была Ricochet Robots, которая по сути является головоломкой со скольжением по льду для нескольких игроков. Мне очень понравилось это задание (и я победил в соревновании!), после чего я продолжил участвовать в соревнованиях в качестве ассистента преподавателя.
Цель этой задачи заключалась в том, чтобы познакомить всех с рекурсией и поиском в глубину. Программе передавались исходное состояние игры, а также максимальная глубина рекурсии. Необходимо было вернуть или кратчайшее решение или все возможные решения минимальной длины. В соревнованиях игрокам могли или сообщать, или не сообщать предел глубины; кроме того, возможны были головоломки, не имеющие решения. Я многому научился и получил кучу удовольствия, так что, возможно, вам это тоже понравится.
Аннотация
В этой статье я представлю новую игру-головоломку и продемонстрирую техники, использованные мной для написания быстрого практичного солвера для неё. Рассматриваются следующие темы: поиск в ширину/поиск A*, мемоизация, оптимизация и стратегии, относящиеся к NP-трудным и NP-полным играм-головоломкам. Если вы найдёте какие-то проблемы или захотите предложить улучшения, то составьте issue или отправьте PR на GitHub. Я представлю бенчмарки, подтверждающие мои результаты. Процентные изменения могут быть относительно точными, а абсолютное время может варьироваться, потому что берётся в разные моменты с разной величиной базового шума.
Бенчмарки до и после изменений всегда выполняются один за другим, чтобы гарантировать, что они работают в одном окружении и демонстрируют точное процентное изменение.
Давайте сыграем в игру
Игра, в которую мы будем играть, называется «Anima». В ней используется сетка из тайлов, каждый из которых проходим или не проходим. Некоторые тайлы помечены маленьким цветным ромбом; эти тайлы являются конечными точками и чтобы решить головоломку, нам нужно одновременно закрыть все эти тайлы акторами того же цвета. Акторы — это блоки, на одном тайле может быть только один блок, который можно перемещать по сетке через проходимые тайлы. В каждый ход можно перемещать акторов в одном из четырёх направлений и все они движутся одновременно. Давайте посмотрим на пару примеров, чтобы понять принцип:
Управление
[Все примеры интерактивны в оригинале статьи.]
- Перемещение: WASD/клавиши со стрелками (десктоп), свайпы (мобильные устройства)
- Отмена: Space (десктоп), кнопка слева вверху
- Сброс: Shift + Space (десктоп), кнопка слева внизу
- Снять фокус: Escape (десктоп), щелчок или касание вне поля (мобильные устройства)
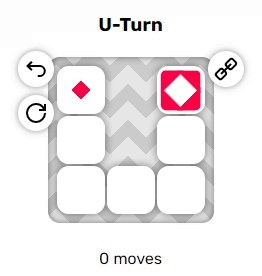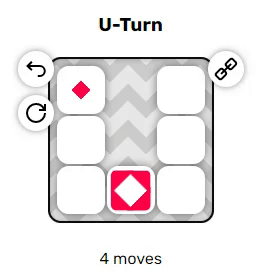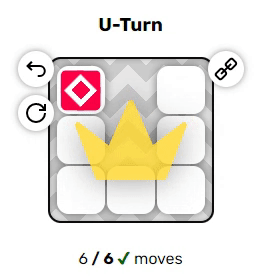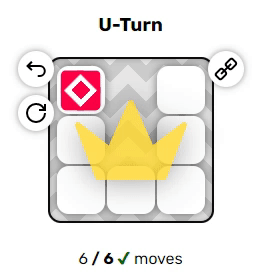
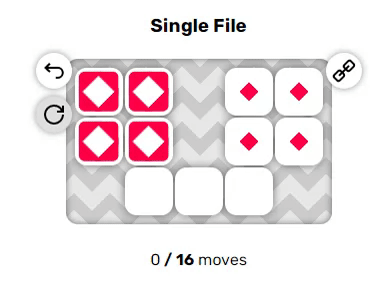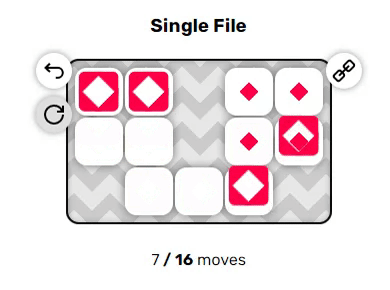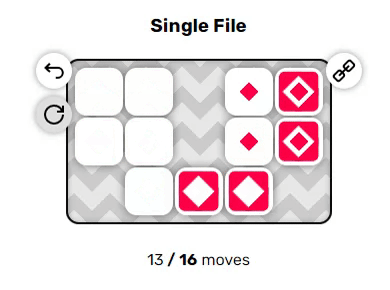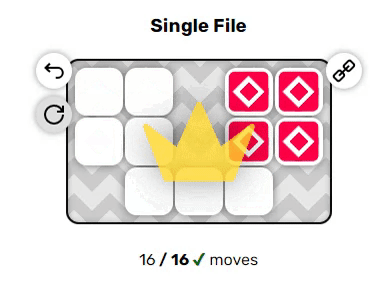
Эти два примера довольно просты, однако вы могли заметить пару неявных правил, из-за которых решение головоломок становится нетривиальным:
- Если актор пытается переместиться на непроходимый тайл, то он не движется.
- Если актор должен наложиться на другого актора, то он не движется.
Из-за этих побочных эффектов очень сложно (или невозможно?) предсказать, как будет вести себя система даже через один-два хода, что является отличительной особенностью задач с высокой NP-сложностью. Мы добавим ещё один неожиданный поворот, чтобы сделать игру немного интереснее:
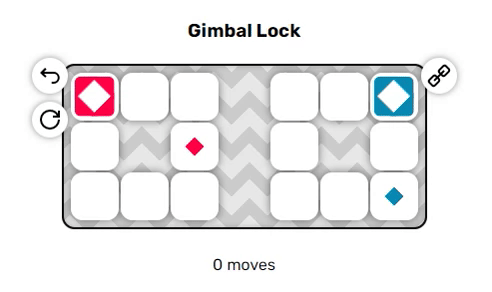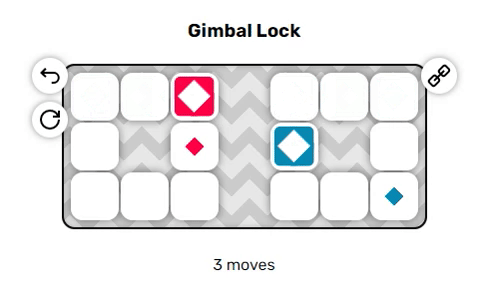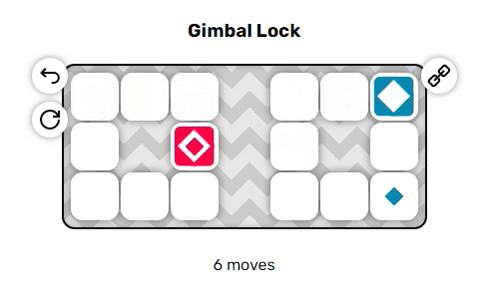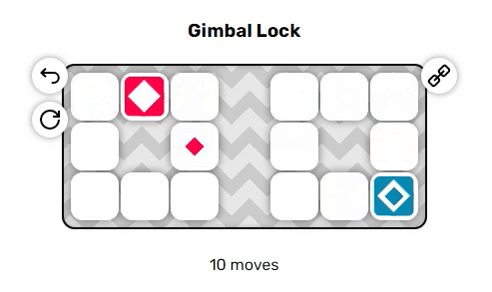
В отличие от красных акторов, синие акторы движутся в направлении, противоположном выбранному вами. Если вы нажмёте влево, синие акторы будут двигаться вправо, и наоборот. Это приводит к последнему неявному правилу:
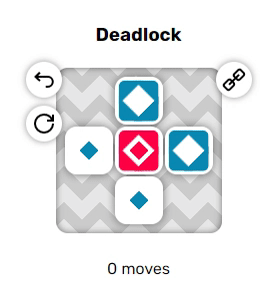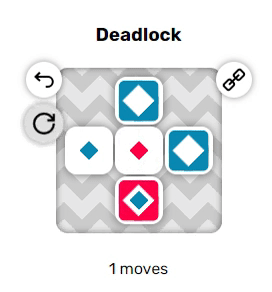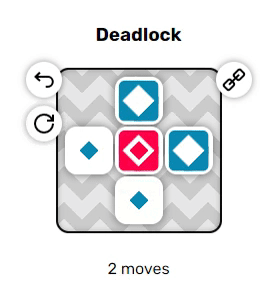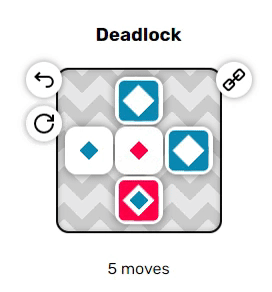
Когда они находятся рядом друг с другом, красные и синие акторы могут проходить проходить друг друга насквозь, меняясь местами. Однако если они разделены одним пустым тайлом, то они попытаются переместиться в одно пространство, а поэтому не вообще не позволят друг другу двигаться. Эта дополнительная трудность может сильно повысить сложность решения головоломок.
Прежде чем мы приступим к разбору, я рекомендую вам поиграть в несколько уровней, чтобы лучше ощутить высокоуровневые техники и лучше познакомиться с игрой. Не волнуйтесь, если не сможете пройти все, они могут быть очень сложными. Просто поиграйте, чтобы ощутить, что достаточно освоились.
Попрактиковаться в решении уровней можно здесь: Puzzles
А теперь мы приступим к написанию солвера. Вы можете следить за процессом при помощи метки start в репозитории GitHub, которая познакомит вас со всем бойлерплейтом:
git clone --branch start https://github.com/djkoloski/anima_solverПростейший солвер
Наша стратегия для простейшего солвера будет заключаться в том, что он, начав из исходного состояния, по одному ходу за раз станет исследование состояний, пока не найдёт решение. Я реализую это при помощи простого поиска в ширину, дополненного отслеживанием родителей:
pub fn solve(initial_state: State, data: &Data) -> Option> {
let mut parents = Vec::new();
let mut queue = VecDeque::new();
// Add transitions from initial state
for (action, transition) in initial_state.transitions(data) {
match transition {
Transition::Indeterminate(state) => {
parents.push((0, action));
queue.push_back(state);
}
Transition::Success => return Some(vec![action]),
}
}
// Pop states in order
let mut index = 0;
while let Some(parent_node) = queue.pop_front() {
index += 1;
for (action, transition) in parent_node.transitions(data) {
match transition {
Transition::Indeterminate(state) => {
parents.push((index, action));
queue.push_back(state);
}
Transition::Success => {
let mut result_actions = vec![action];
let mut current_index = index;
while current_index != 0 {
let (next_index, action) = parents.swap_remove(current_index - 1);
result_actions.push(action);
current_index = next_index;
}
result_actions.reverse();
return Some(result_actions);
}
}
}
}
None
} Я убрал большую часть бойлерплейта, так что вот самое важное:
- У нас есть структуры
StateиData; вStateнаходится вся информация, которая может меняться, а вData— вся статичная информация.State— это позиции акторов, аData— схема поля и позиции конечных точек. Они разделены, чтобы минимизировать объём памяти, используемыйqueue. - Метод
transitions()обрабатываетState, получает данные изDataи возвращает новые состояния, которых мы достигаем, выполняя каждый возможный ход. ПереходIndeterminateозначает, что достигнутое нами состояние нерешено, а переходSuccess— что решено.
parents здесь — это список из (usize, Direction), отслеживающий, из какого состояния он получился и в каком направлении перемещался для перехода. Добравшись до успешного перехода, мы вернёмся через вектор parents, чтобы пересобрать решение и вернуть его. Давайте проверим нашу программу!
Возьмём для этого простую головоломку:

$ cargo run -- puzzles/line_dance.txt
puzzles/line_dance.txt:
Parse: 0.000201900s
Solve: 0.000017600s
Found solution of length 2:
Right, RightЗдорово, и она нашла решение! Оно выглядит правильным. Давайте посмотрим, насколько оно быстрое в режиме релиза:
$ cargo run --release -- puzzles/line_dance.txt
puzzles/line_dance.txt:
Parse: 0.000122700s
Solve: 0.000009100s
Found solution of length 2:
Right, RightПримерно вдвое быстрее, отлично! В дальнейшем мы будем запускать программу только в режиме релиза. Теперь давайте шаг вперёд и попробуем головоломку посложнее:

$ cargo run --release -- puzzles/u_turn.txt
puzzles/u_turn.txt:
Parse: 0.005942000s
Solve: 0.001093200s
Found solution of length 6:
Down, Down, Left, Left, Up, UpПотрясающе, и её программа решила! Ещё одну, она практически такая же:

$ cargo run --release -- puzzles/spiral.txt
...Ой-ёй, похоже, быстро её мы не решим. А если программу не прибить, то и память может закончиться! Посмотрев на тайминги, мы поймём, почему:
puzzles/line_dance.txt
Solve: 0.000009100s
Found solution of length 2:
puzzles/u_turn.txt
Solve: 0.001093200s
Found solution of length 6:После добавления всего четырёх ходов к длине решения время выполнения увеличилось в 120 раз! Давайте посмотрим, сколько состояний мы исследуем:
println!("Explored {} states", parents.len());$ cargo run --release -- puzzles/line_dance.txt
Explored 3 states
$ cargo run --release -- puzzles/u_turn.txt
Explored 5364 states
Ого, вот и проблема. И это логично — каждое исследуемое нами состояние приводит к ещё четырём, поэтому следует ожидать, что для решения длиной n нужно будет исследовать не менее (4^n - 1) / 3 состояний. При решении в 6 ходов получается от 1365 до 5461 состояния, то есть мы попали как раз в этот интервал. Но что это означает для нашей пока нерешённой головоломки? Для её решения требуется 16 ходов, то есть стоит ожидать, что придётся исследовать от 1431655765 до 5726623061 состояния.
Ой-ёй.
Пришло время переработать и усовершенствовать наш солвер. Мы будем измерять улучшение длительностью решений уже имеющихся головоломок, а в дальнейшем будем создавать новые, более сложные. Наша цель — быстро решать все головоломки, которые можно создать.
Отслеживание состояний
Во-первых, мы должны заметить, что несмотря на то, что для U-Turn мы исследовали 5364, функционально существует всего 7 уникальных состояний: по одному для каждого из тайлов, на которых может находиться актор. То есть, получается, мы множество раз исследуем одно и то же состояние. Мы можем избежать этого, сохраняя исследованные состояния во множество хэшей и исследуя только дочернее состояние, если родительское состояние ещё не было посещено:
let mut states = HashSet::new();
...
while let Some(parent_node) = queue.pop_front() {
index += 1;
if !states.contains(&parent_node) {
...
states.insert(parent_node);
}
}Давайте посмотрим, как это повлияет на уже рассмотренные нами случаи:
$ cargo run --release -- puzzles/u_turn.txt
Explored 20 states
Solve: 0.000895100s
Found solution of length 6:
Down, Down, Left, Left, Up, UpВыглядит намного лучше! Может быть, теперь мы сможем решить нашу головоломку?
$ cargo run --release -- puzzles/spiral.txt
Explored 51 states
puzzles/spiral.txt:
Parse: 0.000212300s
Solve: 0.001049000s
Found solution of length 16:
Left, Left, Up, Up, Right, Right, Right, Right, Down, Down, Down, Down, Left, Left, Left, LeftТак гораздо лучше — количество исследуемых состояний снизилось с миллиарда с лишним до всего 51. Одной этой оптимизации оказалось достаточно, чтобы все наши примеры головоломок стало можно решать! Теперь мы можем проводить более комплексные бенчмарки солвера. В качестве бенчмарков выберем несколько представителей из примеров головоломок:
$ cargo bench
solve_square_dance time: [16.658 ms 16.888 ms 17.125 ms]
solve_fractal time: [44.606 ms 45.193 ms 45.806 ms]
solve_antiparticle time: [1.8001 s 1.8308 s 1.8640 s]Снижение энтропии
Простая оптимизация заключается в снижении энтропии состояний. Сейчас наше состояние головоломки выглядит так:
enum Color {
Red,
Blue,
}
pub struct Actor {
position: Vec2,
color: Color,
}
pub struct State {
actors: Vec,
} Представьте поле с несколькими красными акторами на нём. Допустим, их четыре, пометим их как A, B, C и D:

При наличии этих четырёх акторов существует 4! способов представления состояния, поскольку в векторе 4! перестановок акторов. Мы можем исправить это, отсортировав массив actors. При этом все перестановки акторов перестроятся в один канонический порядок. Мы можем довольно легко реализовать это при выполнении перехода между состояниями:
pub fn transition(&self, data: &Data, direction: &Direction) -> State {
let mut result = self.clone();
...
result.actors.sort();
result
}Можно рассматривать это как устранение из состояния ненужной энтропии. Давайте посмотрим, как это повлияет на бенчмарки:
$ cargo bench
solve_square_dance time: [4.4875 ms 4.5667 ms 4.6525 ms]
change: [-73.527% -72.960% -72.308%] (p = 0.00 < 0.05)
solve_fractal time: [19.518 ms 19.647 ms 19.776 ms]
change: [-57.178% -56.527% -55.885%] (p = 0.00 < 0.05)
solve_antiparticle time: [187.49 ms 190.53 ms 193.91 ms]
change: [-89.835% -89.593% -89.343%] (p = 0.00 < 0.05)Посмотрим, как при этом изменилось количество исследуемых состояний (и коэффициент ветвления BF):
| Головоломка | Длина решения | До (BF) | После (BF) | Изменение |
|---|---|---|---|---|
| Square Dance | 12 | 37268 (2.292) | 11401 (2.061) | -61.408% |
| Fractal | 13 | 86277 (2.294) | 46253 (2.179) | -46.390% |
| Antiparticle | 22 | 2514936 (1.888) | 315100 (1.708) | -87.471% |
Чаще всего мы будем стремиться получать подобные серьёзные улучшения при помощи небольших изменений. Здесь важно то, что снизив энтропию состояния, мы немного снизили коэффициент ветвления. Это небольшое изменение в экспоненциальных алгоритмах быстро накапливается, поэтому даже крошечное снижение может привести к очень крупным улучшениям.
Поиск A*
Помня об этом, мы можем сказать, что простым способом дальнейшего снижения коэффициента ветвления может стать использование более сложного алгоритма поиска. A* является очень распространённым усовершенствованием поиска в ширину, отдающим приоритет исследованию более многообещающих узлов. На практике это означает, что нам нужно задать эвристическую функцию, оценивающую минимальное количество ходов до завершения. Мы хотим, чтобы наша эвристическая функция как можно точнее оценивала оставшееся расстояние, но никогда не преувеличивала его. Преуменьшение нас устроит. Имея эту оценку количества оставшихся ходов, мы можем отдавать приоритет исследованию состояний, имеющих минимальный оценочный размер решения (сделанные ходы + оставшиеся ходы). Это позволит не исследовать состояния, которые очевидно являются тупиковыми, и отдавать приоритет состояниям, которые выглядят многообещающе.
Основная сложность с реализацией A* заключается в выборе хорошей эвристической функции. Хорошая эвристическая функция должна быть легко вычисляемой и возвращать максимально высокую оценку, но без преувеличения. Нам нужно полностью осознавать этот компромисс. В большинстве случаев результат будет положительным. Давайте подумаем об эвристике, которую можно вычислить для нашей головоломки:

Чтобы решить головоломку, на каждой конечной точке должен находиться актор соответствующего цвета. Так как все акторы движутся одновременно, мы можем использовать простой maxmin: находить ближайшего к каждой конечной точке актора и вычислять расстояние между ними, а затем брать максимальное значение от всех расстояний до конечных целей. Логически это можно воспринимать так, что мы вычисляем минимальное количество ходов, необходимое для перемещения выбранного актора к любой из конечных точек. Это крайне грубая оценка, но нам она подойдёт. При желании мы могли бы вместо этого вычислить назначения в узких местах, но это может потребовать много времени и отрицательно сказаться на производительности.
pub fn heuristic(&self, data: &Data) -> usize {
let mut max_distance = 0;
for goal in data.goals.iter() {
let mut min_distance = usize::MAX;
for actor in self.actors.iter().filter(|a| a.color == goal.color) {
let d = (goal.position - actor.position).abs();
min_distance = usize::min(min_distance, (d.x + d.y) as usize);
}
max_distance = usize::max(max_distance, min_distance);
}
max_distance
}
Код делает всё то, о чём я рассказал. Самым сложным было адаптировать написанную ранее функцию solve под приоритеты состояний и вычисление эвристики. Первым делом мы объединим в новую структуру всю информацию, необходимую при исследовании узла:
#[derive(Eq, PartialEq)]
struct Node {
state: State,
distance: usize,
estimate: usize,
index: usize,
}Именно это мы теперь будем вставлять в очередь. К слову о ней:
let mut queue = BinaryHeap::new();
BinaryHeap — это простая структура данных, которую можно использовать как очередь с приоритетом. Мы можем вставлять элементы и удалять максимальное значение за время log(N). Для этого достаточно задать упорядочивание узлов, присваивающее самым многообещающим узлам (с наименьшим расстоянием + эвристикой) наибольший приоритет:
impl PartialOrd for Node {
fn partial_cmp(&self, other: &Self) -> Option {
Some(self.cmp(other))
}
}
impl Ord for Node {
fn cmp(&self, other: &Self) -> Ordering {
other.estimate.cmp(&self.estimate)
}
}
Немного непонятно, но в целом этот код просто сообщает, что мы хотим выполнить сортировку в порядке, обратном estimate. Далее нам нужно изменить операцию push, чтобы учесть новые поля, которые необходимо заполнять в fill out в Node:
let estimate = state.heuristic(data) + (parent_node.distance + 1);
queue.push(Node {
state: state,
distance: parent_node.distance + 1,
estimate,
index: parents.len(),
});
Вместо подсчёта состояний сразу после их извлечения нам теперь нужно отслеживать, по какому индексу текущее состояние находится в списке parents. И на этом всё! У нас есть полнофункциональная реализация A*, готовая сделать наш солвер сверхбыстрым!
$ cargo bench
solve_square_dance time: [4.4051 ms 4.4276 ms 4.4524 ms]
change: [+3.7025% +4.6095% +5.4779%] (p = 0.00 < 0.05)
solve_fractal time: [7.7314 ms 7.7718 ms 7.8183 ms]
change: [-57.412% -57.044% -56.682%] (p = 0.00 < 0.05)
solve_antiparticle time: [201.26 ms 202.26 ms 203.36 ms]
change: [+14.570% +15.351% +16.121%] (p = 0.00 < 0.05)Хм, результат немного разочаровывает, по крайней мере, когда смотришь только на отдельные бенчмарки. Результат двух увеличился на 5-15%, а одного — снизился более чем на 50%. То есть хотя выигрыш оказался и ассиметричным, в целом он был нам на пользу. А если теперь нам каким-то образом удастся улучшить эвристическую функцию, то мы получим выигрыш и от неё. Давайте взглянем на исследуемые состояния (и на коэффициент ветвления):
| Головоломка | Длина решения | До (BF) | После (BF) | Разница |
|---|---|---|---|---|
| Square Dance | 12 | 11401 (2.061) | 9737 (2.031) | -14.595% |
| Fractal | 13 | 46253 (2.179) | 16593 (2.002) | -64.126% |
| Antiparticle | 22 | 315100 (1.708) | 269211 (1.695) | -14.563% |
Важно помнить, что выполнять бенчмаркинг нужно очень аккуратно, потому что хотя количество исследованных состояний для всех состояний снизилось, для двух из них увеличилось общее время выполнения. Кроме того, очень небольшое изменение в коэффициенте ветвления для Fractal привело к значительному снижению исследованных состояний. Среднее время выполнения снизилось достаточно неплохо.
Снижаем количество распределений
Первое правило высокопроизводительной оптимизации — снижение количества распределений. Давайте найдём места, в которых это можно сделать:
pub fn transitions(&self, data: &Data) -> Vec<(Direction, Transition)> {
...
}
Функция переходов возвращает Vec с данными, распределёнными в кучу, но мы знаем, что всегда будем возвращать четыре перехода. Поэтому мы можем сделать так, чтобы она возвращала массив:
pub fn transitions(&self, data: &Data) -> [(Direction, Transition); 4] {
...
} Давайте посмотрим, что это нам даст:
$ cargo bench
solve_square_dance time: [4.4052 ms 4.4415 ms 4.4867 ms]
change: [-7.0971% -6.1140% -4.9385%] (p = 0.00 < 0.05)
solve_fractal time: [7.6836 ms 7.7682 ms 7.8720 ms]
change: [-8.5312% -7.0938% -5.5943%] (p = 0.00 < 0.05)
solve_antiparticle time: [207.00 ms 207.71 ms 208.44 ms]
change: [-4.9600% -4.2495% -3.5907%] (p = 0.00 < 0.05)
Довольно скромный выигрыш, поэтому давайте продолжим. Далее мы можем использоват крейт arrayvec для снижения количества распределений в наших состояниях. По сути, это структура массива со встроенным распределением, поэтому мы не будем постоянно распределять память кучи, если можно ограничить сверху количество акторов в головоломках. Чтобы оставить пространство для манёвра, давайте ограничимся восемью:
pub struct State {
actors: ArrayVec,
} Посмотрим на результаты:
$ cargo bench
solve_square_dance time: [4.0299 ms 4.0567 ms 4.0854 ms]
change: [-9.7690% -8.6635% -7.6778%] (p = 0.00 < 0.05)
solve_fractal time: [7.4610 ms 7.5152 ms 7.5743 ms]
change: [-4.6656% -3.2571% -1.9086%] (p = 0.00 < 0.05)
solve_antiparticle time: [187.27 ms 188.29 ms 189.38 ms]
change: [-9.9536% -9.3494% -8.7499%] (p = 0.00 < 0.05)Отлично! Ещё немного скромных улучшений, но пригодится любая мелочь. Наконец, настало время выполнить…
Профилирование
Простые возможности для оптимизации исчерпаны, поэтому давайте перейдём к микрооптимизациям. Мы по-прежнему многое можем выиграть, и выяснится это при помощи профилирования. Запустив бенчмарки в Visual Studio, мы получим интересные наблюдения:

Вот они в текстовом виде:
| Функция | Общий % CPU |
|---|---|
anima_solver::puzzle::State::transitions |
24.40% |
hashbrown::map::HashMap::contains_key |
20.72% |
hashbrown::map::HashMap::insert |
19.83% |
alloc::collections::binary_heap::BinaryHeap::pop |
15.91% |
Сразу становится заметно, что мы тратим почти столько же времени в HashMap::contains_key, сколько и в HashMap::insert. Но ведь в нашем солвере нет hash maps. Или есть?
На самом деле есть. Мы используем HashSet для посещённых состояний, а он является замаскированным HashMap. Давайте взглянем на код:
let mut states = HashSet::new();
...
while let Some(parent_node) = queue.pop() {
if !states.contains(&parent_node.state) {
for (action, transition) in parent_node.state.transitions(data) {
...
}
states.insert(parent_node.state);
}
}
Вот в чём проблема, мы проверяем — содержит ли множество состояние, а затем получаем переходы и после этого вставляем состояние. Наверно, мы сможем использовать Entry API для проверки того, содержит ли множество состояние и для вставки его за одну операцию поиска, так? Ну-у-у… У HashSet пока нет entry API наподобие того, что есть у HashMap.
Ну, тогда мы можем использовать HashMap со значением (), так?
let mut states = HashMap::new();
...
while let Some(parent_node) = queue.pop() {
if let Entry::Vacant(entry) = states.entry(parent_node.state) {
for (action, transition) in entry.key().transitions(data) {
...
}
entry.insert(());
}
}Должно сработать. Давайте посмотрим, как это изменило время выполнения:
$ cargo bench
solve_square_dance time: [3.8785 ms 3.9364 ms 3.9998 ms]
change: [+0.9796% +2.8698% +4.8065%] (p = 0.00 < 0.05)
solve_fractal time: [6.7915 ms 6.8446 ms 6.9022 ms]
change: [-2.2994% -1.2597% -0.0914%] (p = 0.03 < 0.05)
solve_antiparticle time: [172.04 ms 172.76 ms 173.54 ms]
change: [-2.4655% -1.8303% -1.1884%] (p = 0.00 < 0.05)Печально, статистически изменения во времени выполнения отсутствуют. Предполагаю, что у entry API есть какие-то издержки, столь же затратные, как и поиск со вставкой. Если кто-то знает, почему суммарное время выполнения не изменилось, мне бы хотелось знать. Но в то же время это демонстрирует важность бенчмаркинга каждого шага. Даже самые очевидные улучшения в конечном итоге могут никак не повлиять на общую производительность, или даже повлиять отрицательно.
Предварительное задание размеров контейнеров
Мы почти добрались до дна бочки. Мы можем реализовать быструю и простую оптимизацию — заранее задать размер контейнеров. Это поможет нам не выполняют любую потенциальную работу по изменению размера контейнеров под рабочие нагрузки ниже некого минимального размера. Я выбрал относительно произвольные заданные размеры:
let mut states = HashMap::with_capacity(4 * 1024);
let mut parents = Vec::with_capacity(4 * 1024);
let mut queue = BinaryHeap::with_capacity(1024);Стоит ожидать, что они повлияют только на головоломки, не использующие память выше порога заданного размера. Так ли это?
$ cargo bench
solve_square_dance time: [3.7025 ms 3.7311 ms 3.7652 ms]
change: [-9.7612% -8.3409% -6.9754%] (p = 0.00 < 0.05)
solve_fractal time: [6.0512 ms 6.1010 ms 6.1584 ms]
change: [-15.633% -14.231% -12.778%] (p = 0.00 < 0.05)
solve_antiparticle time: [177.28 ms 178.40 ms 179.59 ms]
change: [-0.7913% +0.0458% +0.8882%] (p = 0.92 > 0.05)Именно это мы и видим. В головоломках попроще мы получаем очень хорошие дельты, но на бенчмарки с большими головоломками это совершенно не повлияло. Однако это всё равно снижает время среднестатистического случая, и это для нас важно. Наконец, мы можем перейти к последней стратегии оптимизации.
Встраивание
Один из последних инструментов в инструментарии увеличения производительности — это встраивание функций. Воздействие встраивания функций сильно разнится, нам нужно быть аккуратными и постоянно проверять код бенчмарками. Давайте посмотрим, есть ли подходящие кандидаты на встраивание. В идеале подходящая функция для встраивания должна быть или маленькой, или средней, и использоваться один или два раза. В нашем векторе есть много простых функций, а также присутствуют примитивы директив, которые мы можем встроить, и это немного нам поможет. Встраивание особенно активно использующейся функции transition для состояния головоломки также позволит устранить часть издержек.
Давайте посмотрим, как это влияет на производительность:
$ cargo bench
solve_square_dance time: [3.7629 ms 3.8005 ms 3.8413 ms]
change: [-10.293% -8.6516% -6.9645%] (p = 0.00 < 0.05)
solve_fractal time: [6.7174 ms 6.8059 ms 6.9033 ms]
change: [-10.243% -8.5148% -6.7086%] (p = 0.00 < 0.05)
solve_antiparticle time: [175.97 ms 176.63 ms 177.38 ms]
change: [-6.8481% -5.9110% -5.0767%] (p = 0.00 < 0.05)Наш надёжный набор улучшений готов! Всегда радостно видеть такое.
Подведём итоги
Мы успешно создали солвер головоломок, способный решать задачу при всех возможных входных данных, и оптимизировали его при помощи специализированных методик брутфорса, а также общих методик оптимизации.
Мы рассмотрели влияние различных методик на производительность и знаем теперь, чего ждать в будущем.
Наконец, мы научились не предполагать, что какая-то конкретная оптимизация равномерно повлияет на все случаи, или что она хотя бы повлияет положительно.
В будущем наибольшего выигрыша стоит ожидать от улучшения эвристической функции. Для этой относительно простой игры может и не существовать более качественной эвристики. Однако в более сложной игре мы часто можем использовать информацию из головоломки, чтобы создать гораздо более качественную функцию.
При написании солвера для Stephen's Sausage Roll, позволявшей получить более точную эвристику, выигрыш от эвристической функции был гораздо больше.
Кстати, вы прямо сейчас можете использовать написанный в статье солвер! Его можно включить на любой странице с головоломкой, добавив к URL строку &controls=true (например, здесь).
![[Перевод] Интеллектуальный брутфорс: пишем головоломку и солвер для неё [Перевод] Интеллектуальный брутфорс: пишем головоломку и солвер для неё](https://habrastorage.org/webt/lr/rs/oi/lrrsoigqli7_jgtiwmzpbb21z_y.png)


