![[Перевод] 1000-мерный куб: можно ли сегодня создать вычислительную модель человеческой памяти? [Перевод] 1000-мерный куб: можно ли сегодня создать вычислительную модель человеческой памяти?](https://habrastorage.org/webt/hm/bf/hq/hmbfhq9wergzhrrb1fskxsurpsk.png)
Сегодня утром на пути к кампусу Беркли я провёл пальцами по листьям ароматного куста, а затем вдохнул знакомый запах. Я делаю так каждый день, и каждый день первое слово, которое всплывает в голове и приветственно машет рукой — это шалфей (sage). Но я знаю, что это растение — не шалфей, а розмарин, поэтому я приказываю шалфею успокоиться. Но слишком поздно. После rosemary и sage я не могу помешать появлению на сцене петрушки (parsley) и чабреца (thyme), после чего в голове возникают первые ноты мелодии и лица на обложке альбома, и вот я уже снова оказался в середине 1960-х, одетый в рубашку с огурцами. Тем временем розмарин (rosemary) вызывает в памяти Роуз Мэри Вудс (Rosemary Woods) и 13-минутный пробел (хотя теперь, проконсультировавшись с коллективной памятью, я знаю, что это должны быть Роуз Мэри Вудс и пробел в 18 с половиной минут). От Уотергейта я перепрыгиваю к историям на главной странице. Потом я замечаю в ухоженном саду ещё одно растение с пушистыми серо-зелёными листями. Это тоже не шалфей, а чистец (lamb’s ear). Тем не менее, sage наконец получает свою минуту славы. От трав я переношусь к математическому ПО Sage, а потом к системе противовоздушной обороны 1950-х под названием SAGE, Semi-Automatic Ground Environment, которой управлял самый крупный из когда-либо построенных компьютеров.
В психологии и литературе подобные мыслительные блуждания называются потоком сознания (автор этой метафоры — Уильям Джеймс). Но я бы выбрал другую метафору. Моё сознание, насколько я ощущаю, не течёт плавно от одной темы к другой, а скорее порхает по ландшафту мыслей, больше похожее на бабочку, чем на реку, иногда прибиваясь к одному цветку, а затем к другому, иногда уносимая порывами ветка, иногда посещающая одно и то же место снова и снова.
Чтобы исследовать архитектуру собственной памяти я попытался провести более неспешный эксперимент со свободными ассоциациями. Я начал с того же флорального рецепта — петрушка, шалфей, розмарин и чабрец — но для этого упражнения не прогуливался по садам холмов Беркли; я сидел за столом и делал заметки. Показанная ниже схема представляет собой наилучшую попытку реконструкции полного хода моих размышлений.
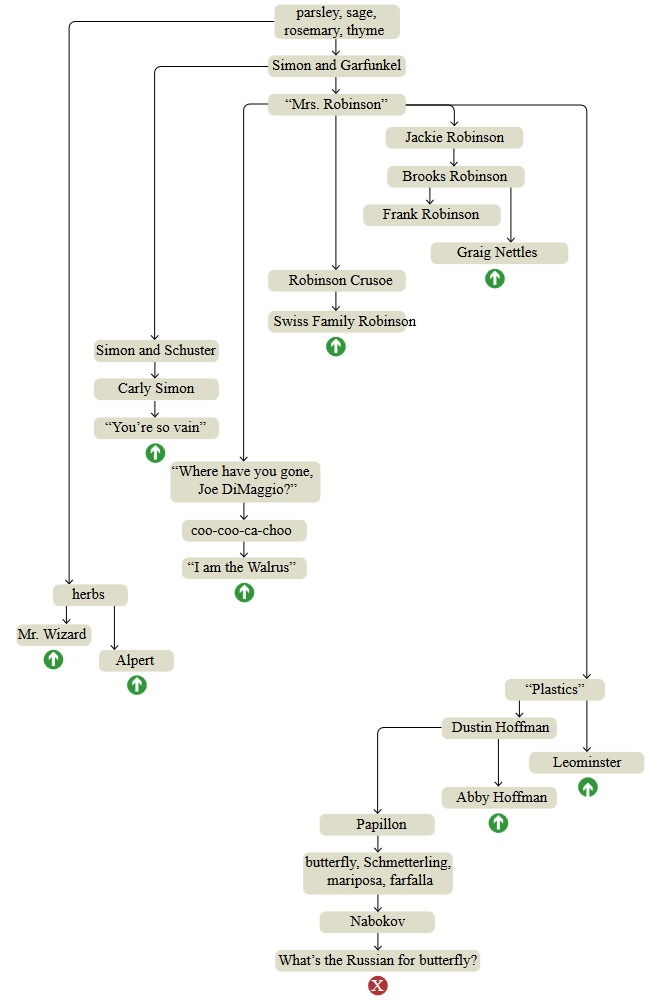
parsley, sage, rosemary, thyme — четыре травы, а также строчка из песни Simon and Garfunkel.
Simon and Garfunkel — Пол Саймон и Арт Гарфанкел, дуэт певцов в жанре фолк-рока 1960-х и 70-х.
Mrs. Robinson — песня Simon and Garfunkel, а также персонаж из фильма Майка Николса «The Graduate».
«Where have you gone, Joe DiMaggio?» — вопрос, задаваемый в «Mrs. Robinson».
Simon and Schuster — издательский дом, основанный в 1924 году Ричардом Саймоном и Максом Шустером (изначально для публикации кроссвордов).
Джеки Робинсон — легендарный игрок Brooklyn Dodgers.
Робинзон Крузо — роман Даниэля Дефо о потерпевшем кораблекрушение (1719 год).
Швейцарская семья Робинзонов — роман Йохана Дэвида Уайсса о потерпевших кораблекрушение (1812 год).
herbs (травы) — ароматные растения
Mr. Wizard — субботнее научное шоу 1950-х для детей, ведущий Дон Херберт.
Alpert — трубач Герб Алперт.
«Plastics» — совет по карьерному росту, предложенный в «The Graduate».
coo-coo-ca-choo — строчка из «Mrs. Robinson».
Фрэнк Робинсон — аутфилдер Baltimore Orioles в 1970-х.
Грэйг Неттлз — третий бейсмен New York Yankees в 1970-х.
Дастин Хоффман — актёр, игравший в «The Graduate».
Эбби Хоффман — «Yipee!»
Леоминстер — город в Массачусетсе, ставший колыбелью производства пластмасс в США.
Брукс Робинсон — третий бейсмен Baltimore Orioles в 1970-х.
Papillon («Мотылёк») — фильм 1973 года, в которой Дастин Хоффман исполнял второстепенную роль; «papillon» по-французски «бабочка».
Nabokov — Владимир Набоков, родившийся в России писатель и изучающий бабочек энтомолог.
butterfly, Schmetterling, mariposa, farfalla — «бабочка» на английском, немецком, испанском и итальянском; похоже, что все они (и французское слово тоже) имеют независимое происхождение.
Как по-русски называется бабочка — я не знаю. Или не знал, когда возник этот вопрос.
«I am the Walrus» — песня Beatles 1967 года, в которой тоже есть фраза «coo-coo-ca-choo».
Карли Саймон — певица. Никакой связи с Полом Саймоном, но является дочерью Ричарда Саймона.
«You’re so vain» — песня Карли Саймон.
График сверху вниз представляет собой темы в том порядке, котором они всплывали в мозгу, но связи между узлами не создают единую линейную последовательность. Структура напоминает дерево с короткими цепочками последовательных ассоциаций, заканчивающиеся резким возвратом к более раннему узлу, как будто меня утащило обратно растянувшейся резиновой лентой. Такие прерывания помечены на графике зелёными стрелками; красный крестик внизу — это место, на котором я решил завершить эксперимент.
Прощу прощения у тех, кто родился позже 1990 года, многие из упомянутых тем могут показаться вам устаревшими или загадочными. Под графиком представлены объяснения, однако не думаю, что они сделают ассоциации более понятными. В конце концов, воспоминания персональны, они живут внутри головы. Если вы хотите собрать коллекцию идей, соответствующих вашему собственному опыту, вам достаточно создать собственный график свободных ассоциаций. Крайне рекомендую сделать это: вы можете обнаружить что вы не знали, что знаете какие-то вещи.
Целью моей ежедневной прогулки вниз по холму в Беркли является Институт Саймонса и курс теории вычислений, в котором я участвую в длящейся один семестр программе, посвящённой мозгу и вычислениям. Такое окружение вызывает мысли о мыслях. Я начал размышлять: каким образом можно построить вычислительную модель процесса свободных ассоциаций? Среди различных задач, предлагаемых для решения искусственным интеллектом, эта выглядит довольно просто. Здесь нет необходимости в глубокой рационализации; всё, что нам нужно симулировать — это просто грёзы и витание в облаках — именно этим занимается мозг, когда он не нагружен. Похоже, что такую задачу решить легко, не правда ли?
Первая идея, которая приходит в голову (по крайней мере, в мою голову), относительно архитектуры такой вычислительной модели — это случайное движение по математическому графу или сети. Узлы сети — это хранящиеся в памяти элементы — идеи, факты, события — а связи — это различные виды ассоциаций между ними. Например, узел «бабочка» может быть связан с «мотыльком», «гусеницей», «монархом» и «перламутровкой», а ещё с переходами, упомянутыми в моём графике, и, возможно, иметь и менее очевидные связи, например «Australian crawl», «креветка», «Мохаммед Али», «пеллагра», «дроссель» и «страх сцены». Структура данных узла сети будет содержат список указателей на все эти связанные узлы. Указатели могут быть пронумерованы от 1 до n; программа будет генерировать псевдослучайное число в этом интервале и переходить к соответствующему узлу, в котором вся процедура будет начинаться заново.
Этот алгоритм отражает некоторые основные характеристики свободных ассоциаций, но многие из них не учитывает. Модель предполагает, что все целевые узлы равновероятны, что выглядит неправдоподобно. Чтобы учесть разницу вероятностей, мы можем задать каждому ребру вес , а затем сделать вероятности пропорциональными весам.
Ещё больше усложняет всё тот факт, что веса зависят от контекста — от недавней истории умственной активности человека. Если бы у меня не было сочетания Mrs. Robinson и Джеки Робинсона, то подумал ли бы я о Джо Ди Маджо? А сейчас, когда я пишу это, Joltin’ Joe (прозвище Ди Маджо) вызывает в памяти Мэрилин Монро, а затем Артура Миллера, и я снова не могу остановить ход размышлений. Для воспроизведения этого эффекта в компьютерной модели потребуется некий механизм динамической регуляции вероятностей целых категорий узлов в зависимости от того, какие другие узлы были посещены недавно.
Также следует учесть эффекты новизны другого вида. В модели должна найти место резиновая лента, постоянно притягивающая меня обратно к Simon and Garfunkel и Mrs. Robinson. Вероятно, каждый недавно посещённый узел необходимо добавить в список вариантов целей, даже если он никак не связан с текущим узлом. С другой стороны, привыкание — это тоже вероятность: слишком часто вспоминаемые мысли становятся скучными, поэтому должны подавляться в модели.
Ещё одно, последнее испытание: некоторые воспоминания являются не изолированными фактами или идеями, а частями истории. У них есть нарративная структура с событиями, разворачивающимися в хронологическом порядке. Для узлов таких эпизодических воспроминаний требуется ребро next, а возможно и previous. Такая цепочка рёбер объединяет всю нашу жизнь, включая в себя всё, что вы помните.
Может ли подобная вычислительная модель воспроизвести мои умственные блуждания? Сбор данных для такой модели окажется довольно долгим процессом, и это неудивительно, ведь мне понадобилась вся жизнь, чтобы заполнить свой череп переплетением трав, Гербов, Саймонов, Робинсонов и Хоффманов. Гораздо больше, чем объём данных, меня волнует кропотливость алгоритма обхода графа. Очень легко сказать: «выбери узел согласо множеству взвешенных вероятностей», но когда я смотрю на грязные подробности реализации этого действия, то с трудом могу представить, что нечто подобное происходит в мозге.
Вот простейший из известных мне алгоритм для случайного взвешенного выбора. (Это не самый эффективный из таких алгоритмов, но методы получше ещё более хаотичны. Кит Шварц написал отличный туториал и обзор по этой теме.) Предположим, что структура данных, имитирующая узел сети, включает в себя список связей с другими узлами и соответствующий список весов. Как показано на рисунке ниже, программа генерирует ряд накапливаемых сумм весов: . Следующий шаг заключается в нормализации этого ряда делением каждого числа на общую сумму весов. Теперь у нас есть ряд чисел , монотонно возрастающий от нуля до единицы. Далее программа выбирает случайное вещественное число из интервала ; должно находиться в одном из нормализованных интервалов , а это значение определяет следующий выбираемый узел.
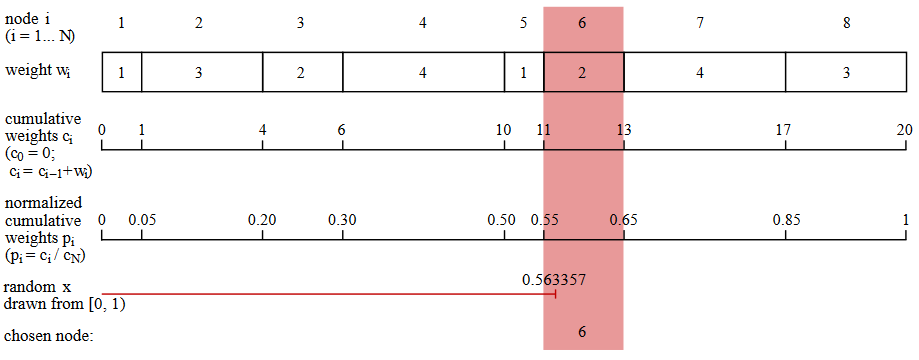
В коде на языке программирования Julia процедура выбора узла выглядит так:
function select_next(links, weights) total = sum(weights) cum_weights = cumsum(weights) probabilities = cum_weights / total x = rand() for i in 1:length(probabilities) if probabilities[i] >= x return i end end endЯ так медленно описываю эти скучные подробности накапливаемых сумм и псевдослучайных чисел, чтобы подчеркнуть таким образом, что этот алгоритм обхода графа не так прост, как выглядит на первый взгляд. И мы всё ещё пока не рассмотрели тему изменения вероятностей на лету, хотя наше внимание плавает от темы к теме.
Ещё сложнее постичь процесс обучения — добавления в сеть новых узлов и рёбер. Я закончил мой сеанс свободных ассоциаций, когда пришёл к вопросу, на который не мог ответить: как по-русски называется бабочка? Но теперь я могу на него ответить. В следующий раз, когда я буду играть в эту игру, я добавлю в список слово babochka. В вычислительной модели вставка узла для слова babochka — это довольно простая задача, но наш новый узел также должен быть связан со всеми уже существующими узлами о бабочках. Более того, babochka сама по себе добавляет новые рёбра. Она фонетически близка к babushka (бабушка) — одному из нескольких русских слов в моём словаре. Суффикс -ochka уменьшительный, поэтому его нужно ассоциировать с французским -ette и итальянским -ini. Буквальное значение слова babochka — «маленькая душа», что предполагает ещё большее количество ассоциаций. В конце концов, изучение единственного нового слова может потребовать полной переиндексации всего дерева знаний.
Давайте попробуем другой метод. Забудем о случайном обходе сети с её спагетти из указателей на узлы. Вместо этого давайте просто хранить все схожие вещи по соседству. С точки зрения банков памяти цифрового компьютера это значит, что схожие вещи будут храниться по соседним адресам. Вот гипотетический сегмент памяти, центрированный на концепции dog. Соседние места заняты другими словами, понятиями и категориями, которые скорее всего будут вызваны мыслью о собаке (dog): очевидные cat (кошка) и puppy (щенок), различные породы собак и несколько конкретных собак (Скиппи — это наш семейный пёс, который был у меня в детстве), а также, возможно, более сложные ассоциации. У каждого элемента есть цифровой адрес. Адрес не имеет какого-то глубинного значения, но важно то, что все ячейки памяти пронумерованы по порядку.
| адрес | содержимое |
|---|---|
| 19216805 | god |
| 19216806 | the dog that didn’t bark in the night |
| 19216807 | Skippy |
| 19216808 | Lassie |
| 19216809 | canine |
| 19216810 | cat |
| 19216811 | dog |
| 19216812 | puppy |
| 19216813 | wolf |
| 19216814 | cave canem |
| 19216815 | Basset Hound |
| 19216816 | Weimaraner |
| 19216817 | dogmatic |
Задача неторопливого блуждания по этому массиву в памяти может быть довольно простой. Она может выполнять случайный обход адресов памяти, но преимущество будет отдаваться небольшим шагам. Например, следующий посещаемый адрес может определяться сэмплированием из нормального распределения, центрированного относительно текущего места. Вот код на Julia. (Функция randn() возвращает случайное вещественное число, полученное из нормального распределения со средним значением и стандартным отклонением .)
function gaussian_ramble(addr, sigma) r = randn() * sigma return addr + round(Int, r) endУ такой схемы есть привлекательные черты. Нет необходимости сводить в таблицу все возможные целевые узлы, прежде чем выбирать один из них. Вероятности не хранятся как числа, а закодированы позицией в массиве, а также модулированы параметром , который определяет, насколько далеко процедура хочет перемещаться в массиве. Хотя программа всё равно выполняет арифметические действия для сэмлирования из нормального распределения, такая функция, вероятно, будет более простым решением.
Но всё-таки у этой процедуры есть ужасающий изъян. Окружив dog всеми его непосредственными ассоциациями, мы не оставили места для их ассоциаций. Собачьи термины хороши в своём собственном контексте, но как насчёт cat из списка? Куда нам поместить kitten, tiger, nine lives и Felix? В одномерном массиве нет никакой возможности встроить каждый элемент памяти в подходящее окружение.
Так что давайте перейдём в два измерения! Разделив адреса на два компонента, мы задаём две ортогональные оси. Первая половина каждого адреса становится координатой , а вторая — координатой . Теперь dog и cat по-прежнему остаются близкими соседями, но также у них появляются личные пространства, в которых они могут играть с собственными «друзьями».
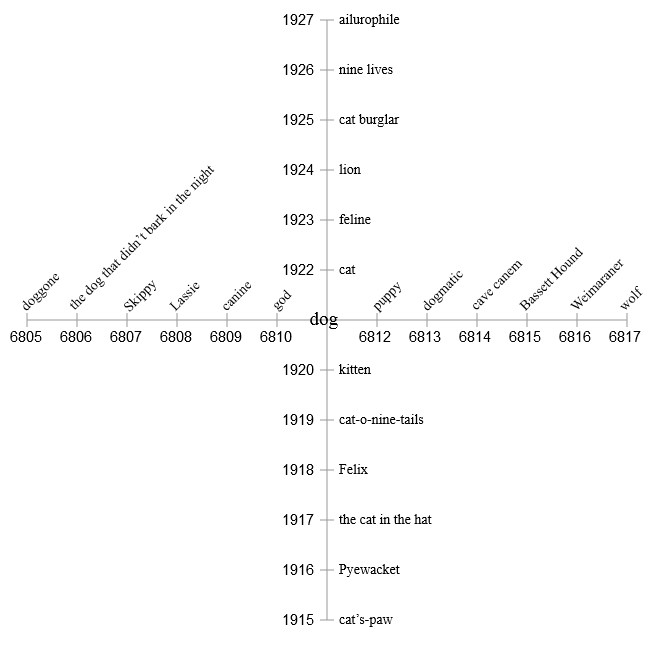
Однако двух измерений тоже недостаточно. Если мы попытаемся заполнить все элементы, связанные с The Cat in the Hat, они неизбежно начнут сталкиваться и конфликтовать с близкими элементами the dog that didn’t bark in the night. Очевидно, нам нужно больше измерений — намного больше.
Сейчас подходящий момент для того, чтобы признаться — я не первый, кто думал о том, как могут быть упорядочены воспоминания в памяти. Список моих предшественников можно начать с Платона, который сравнивал память с птицей; мы распознаём воспоминания по их оперению, но иногда нам трудно достать их, если они начинают порхать в клетке нашего черепа. Иезуит 16-го века Маттео Риччи писал о «дворце памяти», в котором мы блуждаем по различным комнатам и коридорам в поисках сокровищ прошлого. Современные теории памяти обычно менее образны, однако более подробны и нацелены на переход от метафоры к механизму. Лично мне больше всего нравится математическая модель, полученная в 1980-х Пентти Канерва, который сейчас работает в Редвудском центре теоретических нейронаук здесь, в Беркли. Он придумал идею разреженной распределённой памяти (sparse distributed memory), которую я буду называть SDM. В ней удачно применяется удивительная геометрия пространств высокой размерности.
Представьте куб в трёх измерениях. Если принять, что длина стороны равна единице измерения, то восемь векторов можно обозначить векторами из трёх двоичных цифр, начиная с и заканчивая . В любой из вершин изменение единственного бита вектора приводит нас к вершине, являющейся ближайшим соседом. Изменение двух битов перемещает нас к следующему по близости соседу, а замена всех трёх битов приводит к противоположному углу куба — к самой отдалённой вершине.
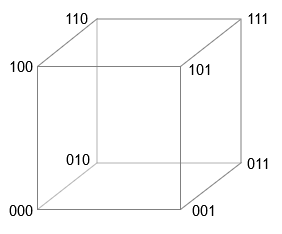
Четырёхмерный куб работает аналогичным образом — вершин обозначены векторами, содержащими все сочетания двоичных цифр, начиная и заканчивая . Это описание на самом деле обобщается до измерений, где каждая вершина имеет -битный вектор координат. Если мы будем измерять расстояние по манхэттанской метрике — всегда перемещаясь вдоль рёбер куба и никогда не срезая по диагонали — то расстояние между любыми двумя векторами будет количеством позиций, в которых отличаются два вектора координат (оно также известно как расстояние Хэмминга). (Для исключающего ИЛИ обычно используют символ ⊕, иногда называемый булочкой (bun). Он отображает операцию XOR как двоичное сложение по модулю 2. Канерва предпочитает ∗ или ⊗ на том основании, что роль XOR в высокоразмерных вычислениях больше похожа на умножение, чем на сложение. Я решил устраниться от этого противоречия, воспользовавшись символом ⊻ — альтернативным способом записи XOR, привычным в среде логиков. Это модификация ∨ — символа включающего ИЛИ. Удобно, что он также является символом XOR в программах на Julia.) Таким образом, единицей измерения расстояния является один бит, а вычисление расстояния — это задача для оператора двоичного исключающего ИЛИ (XOR, ⊻), который даёт нам для отличающихся битов значение , а для одинаковых пар — значение :
0 ⊻ 0 = 0 0 ⊻ 1 = 1 1 ⊻ 0 = 1 1 ⊻ 1 = 0Функция на Julia для измерения расстояния между вершинами применяет функцию XOR к двум векторам координат и возвращает в качестве результата количество .
function distance(u, v) w = u ⊻ v return count_ones(w) endКогда становится достаточно большим, проявляются некоторые любопытные свойства -куба. Рассмотрим -мерный куб, имеющий вершин. Если случайным образом выбрать две его вершины, то каким будет ожидаемое расстояние между ними? Хотя это и вопрос о расстоянии, но мы можем ответить на него, не углубляясь в геометрию — это всего лишь задача подсчёта позиций, в которых различаются два двоичных вектора. Для случайных векторов каждый бит может быть с равной вероятностью быть равным или , поэтому ожидается, что векторы будут различаться в половине битовых позиций. В случае -битного вектора стандартное расстояние равно битам. Такой результат нас не удивляет. Однако стоит заметить то, что все расстояния между векторами тесно скапливаются вокруг среднего значения в 500.
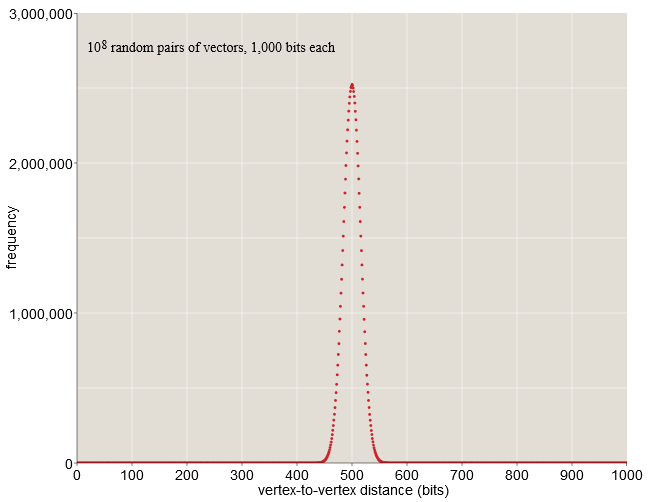
В случае -битных векторов почти все случайно выбранные пары находятся на расстоянии от до бит. В выборке из ста миллионов случайных пар (см. график выше) ни одна из них не ближе, чем бит или дальше, чем бит. Ничто в нашей жизни в пространстве низкого разрешения не готовило нас к такому скоплению вероятностей в среднем расстоянии. Здесь, на Земле, мы можем найти место, в котором будем совсем одни, когда почти все находятся в нескольких тысячах километров от нас; однако нет никакого способа перераспределить население планеты таким образом, чтобы каждый одновременно находится в таком состоянии. Но в -мерном пространстве ситуация именно такова.
Не стоит и говорить, что сложно представить себе -мерный куб, но мы можем приобрести небольшое интуитивное понимание геометрии хотя бы на примере пяти измерений. Ниже представлена таблица всех координат вершин в пятимерном кубе единичной размерности, выстроенных в соответствии с расстоянием Хэмминга от исходной точки . Большинство вершин (20 из 32) находится на средних расстояниях — два или три бита. Таблица имела бы одинаковую форму при любой другой вершине, взятой в качестве исходной точки.

Серьёзное возражение всем этим обсуждениям -мерных кубов заключается в том, что мы никогда не сможем построить нечто подобное; во Вселенной недостаточно атомов для структуры из частей. Но Канерва указывает на то, что нам нужны пространства для хранения только тех элементов, которые мы хотим хранить. Мы можем сконструировать оборудование для случайной выборки, например вершин (каждая из которых имеет -битный адрес) и оставить остальную часть куба призрачной, недостроенной инфраструктурой. Канерва называет такое подмножество вершин, существующее в «железе», твёрдыми ячейками (hard locations). Множество из случайных твёрдых ячеек всё равно будет демонстрировать то же сжатое распределение расстояний, что и полный куб; именно это и показано на графике выше.
Относительная изоляция каждой вершины в высокоразмером кубе даёт нам намёк на одно возможное преимущество разряжённой распределённой памяти: у хранящегося элемента есть достаточно простора и он может распределяться по обширной области, не мешая своим соседям. Это действительно выдающаяся характеристика SDM, но есть и кое-что ещё.
В традиционной компьютерной памяти адреса и хранимые элементы данных сопоставляются один к одному. Адреса — это порядковые целые числа фиксированного диапазона, допустим . Каждое целое число в этом диапазоне определяет единственное отдельное место в памяти, и каждое место связано ровно с одним адресом. Кроме того, в каждом месте одновременно хранится только одно значение; при записи нового значения старое переписывается.
SDM нарушает все эти правила. Она обладает огромным адресным пространством — не менее — но только крошечная, случайная доля этих мест существует как физические сущности; именно поэтому память называется разреженной. Отдельный элемент информации не хранится всего в одном месте памяти; множество копий распределено по области — поэтому она распределённая. Более того, в каждом отдельном адресе может одновременно храниться несколько элементов данных. То есть информация и размазана по широкой области, и втиснута в одну точку. Такая архитектура также размывает различия между адресами памяти и содержимым памяти; во многих случаях сохраняемый битовый паттерн используется в качестве собственного адреса. Наконец, память может отзываться на частичный или приблизительный адрес и с высокой вероятностью находить правильный элемент. В то время как традиционная память является «механизмом точного совпадения», SDM — это «механизм наилучшего совпадения», возвращающий элемент, наиболее схожий с запрошенным.
В своей книги 1988 года Канерва даёт подробный количественный анализ разреженной распределённой памяти с измерениями и твёрдых ячеек. Твёрдые ячейки выбираются случайным образом из всего пространства возможных векторов адресов. Каждая твёрдая ячейка имеет пространство для хранения множества -битных векторов. Память в целом рассчитана на хранение не менее уникальных паттернов. Ниже я буду рассматривать эту память как каноническую SDM-модель, несмотря на то, что по стандартам млекопитающих она маловата, и в более новой своей работе Канерва сделал упор на векторы не менее чем с измерений.
Вот как работает память в простой компьютерной реализации. Команда store(X) записывает в память вектор , считая его одновременно и адресом, и содержимым. Значение сохраняется во все твёрдые ячейки, находящиеся в пределах определённого расстояния до . В канонической модели это расстояние равно 451 битам. Оно задаёт «круг доступа», предназначенного для объединения в себе примерно твёрдых ячеек; иными словами, каждый вектор хранится примерно в -ной из миллиона твёрдых ячеек.
Важно также заметить, что хранимый элемент не обязательно выбирать из двоичных векторов, являющихся адресами твёрдых ячеек. Напротив. может быть любым из возможных двоичных паттернов.
Предположим, что в SDM уже записана тысяча копий , после чего поступает новый элемент , который тоже нужно сохранить в собственном множестве из тысячи твёрдых ячеек. Между двумя этими множествами может быть пересечение — места, в которых хранятся и , и . Новое значение не перезаписывает и не заменяет предыдущее; оба значения сохраняются. Когда память заполняется до своей ёмкости в , каждый из них сохранён раз, а в типичной твёрдой ячейке будут храниться копии уникальных паттернов.
Теперь вопрос заключается в следующем: как же нам воспользоваться этой перемешанной памятью? В частности, как нам получить правильное значение , не влияя на и на все остальные элементы, накопившиеся в одном месте хранения?
В алгоритме считывания будет использоваться свойство любопытного распределения расстояний в высокоразмерном пространстве. Даже если и являются ближайшими соседями из хранящихся паттернов, они скорее всего будут отличаться на 420 или 430 бит; поэтому количество твёрдых ячеек, в которых хранятся оба значения, достаточно мало — обычно четыре, пять или шесть. То же самое относится и ко всем другим паттернам, пересекающимся с . Их тысячи, но ни один из влияющих паттернов не присутствует более чем в нескольких копиях внутри круга доступа .
Команда fetch(X) должна возвращать значение, ранее записанное командой store(X). Первый этап в воссоздании значения — это сбор всей информации, хранящейся внутри 451-битного круга доступа, центрированного на . Поскольку ранее был записан во все эти места, мы можем быть уверены, что получим его копий. Мы также получим около копий других векторов, хранящихся в местах, в которых круги доступа пересекаются с с кругами . Но поскольку пересечения малы, каждый из этих векторов присутствует только в нескольких копиях. Тогда в целом каждый из их бит равновероятно может быть или . Если мы применим функцию принципа большинства ко всем данным, собранным в каждой битовой позиции, то в полученном результате будут доминировать копий . Вероятность получения отличающегося от результата примерно равна .
Процедура принципа большинства подробнее показана ниже на небольшом примере из пяти векторов данных по 20 битов каждый. Выходными данными будет являться другой вектор, каждый бит которого отражает большинство соответствующих битов в векторах данных. (Если количество векторов данных чётное, то «ничьи» разрешаются случайным выбором или .) Альтернативная схема записи и чтения, показанная ниже, отказывается от хранения всех паттернов по отдельности. Вместо этого она хранит итоговое количество битов и в каждой позиции. Твёрдая ячейка имеет -битный счётчик, инициализируемый всеми нулями. При записи паттерна в место каждый битовый счётчик увеличивается для или уменьшается для . Алгоритм считывания просто смотрит на знак каждого битового счётчика, возвращая для положительного значения, для отрицательного и случайное значение, когда бит счётчика равен .

Две эти схемы хранения дают идентичные результаты.
С точки зрения вычислительной техники эта версия разреженной распределённой памяти выглядит как тщательно продуманная шутка. Для запоминания элементов нам понадобится миллион твёрдых ячеек, в которых мы будем хранить тысячу избыточных копий каждого паттерна. Для извлечения всего одного элемента из памяти мы собираем данные по сохранённым паттернам и применяем для их распутывания механизм принципа большинства. И всё это выполняется с помощью кучи акробатических маневров только для получения вектора, который у нас и так уже есть. Традиционная память работает гораздо менее хаотично: и запись, и считывание получают доступ к одному месту.
Но SDM может делать то, на что неспособна традиционная память. В частности, она может извлекать информацию на основе частичных или приблизительных данных. Допустим, вектор является повреждённой версией , в котором изменились из векторов. Поскольку два вектора схожи, команда fetch(Z) посетит множество из тех же мест, в которых хранится . При расстоянии Хэмминга в 100 можно ожидать, что у и будут общими примерно 300 твёрдых ячеек. Благодаря этому большому пересечению вектор, возвращаемый fetch(Z) (назовём его ) будет ближе к , чем является . Теперь мы можем повторить этот процесс с командой fetch(Z′), который вернёт результат , ещё более близкий к . Всего через несколько итераций процедура достигнет самого .
Канерва показал, что сходящаяся последовательность рекурсивных операций считывания приведёт к успеху с почти полной уверенностью, если начальный паттерн не слишком далёк от целевого. Другими словами, существует критический радиус: любая проверка памяти, начиная с места внутри критического круга почти совершенно точно сойдётся к центру, и сделает это довольно быстро. Попытка восстановления элемента, хранящегося за пределами критического круга, закончится неудачей, поскольку рекурсивный процесс вспоминания будет отдаляться на среднее расстояние. В анализе Канерва показано, что для канонической SDM критический радиус равен 209 битам. Другими словами, если мы знаем приблизительно 80 процентов битов, то сможем воссоздать весь паттерн.
На иллюстрации ниже отслеживается эволюция последовательностей рекурсивных воспоминаний с помощью исходных сигналов, отличающихся от целевого на . В этом эксперименте все последовательности, начинающиеся с расстояния или менее, сходятся к за или менее итераций (синие следы). Все последовательности, начинающиеся при бОльшем исходном расстоянии, бесцельно блуждают по огромным пустым пространствам -мерного куба, оставаясь примерно в 500 битах от любого места.
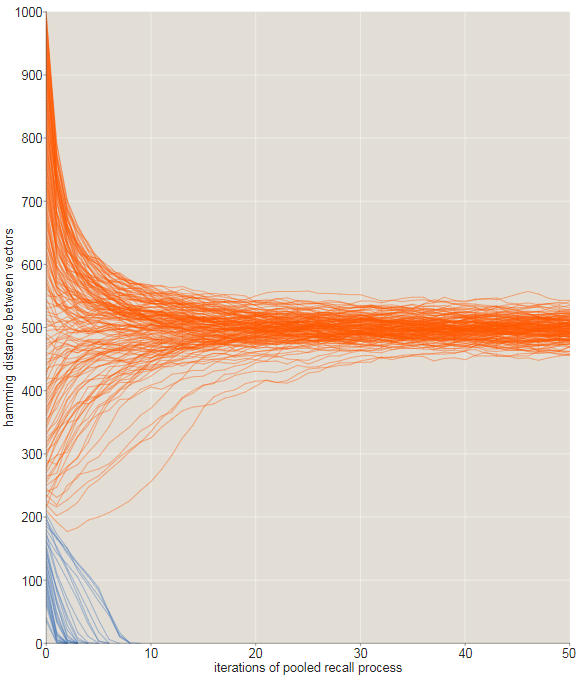
Переход от сходящихся к расходящимся траекториями не идеально чёток, и это заметно на показанном ниже растрёпанном графике. Здесь мы увеличили масштаб, чтобы посмотреть на судьбу траекторий, начинающихся со смещений в бит. Все начальные точки, находящиеся в пределах 209 бит от цели, обозначены синим; начинающиеся с бОльшего расстояния — оранжевые. Большинство из синих траекторий сходится, быстро переходя к нулевому расстоянию, а большинство оранжевых — нет. Однако вблизи от критического расстояния есть множество исключений.
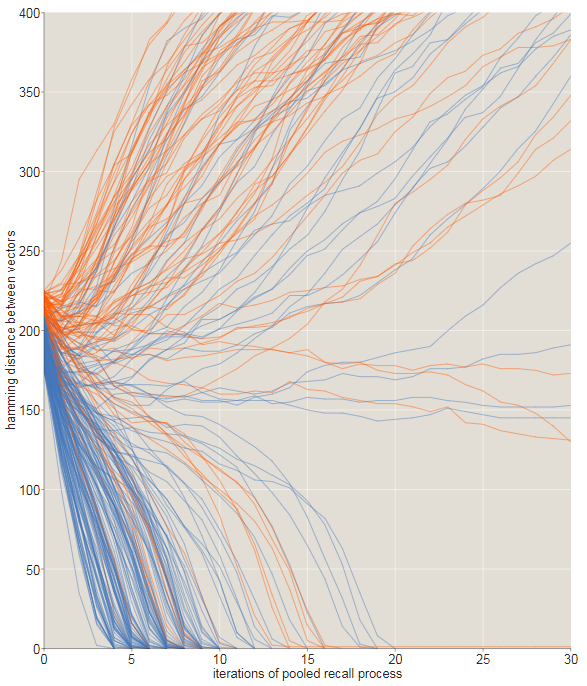
На показанном ниже графике изображён ещё один взгляд на то, как исходное расстояние от цели влияет на вероятность схождения к верному адресу памяти. При расстоянии в бит успехом оканчиваются почти все попытки; при почти все неудачны. Похоже, что точка пересечения (в которой успех и неудача равновероятны) лежит примерно в битах, немного ниже результата Канерва, равного . (В этом расхождении нет ничего загадочного. В вычислениях Канерва предполагается круг доступа ограничивающий ровно твёрдых ячеек. В мои эксперименты включены все твёрдые ячейки в пределах расстояния ; в среднем существует таких мест.)
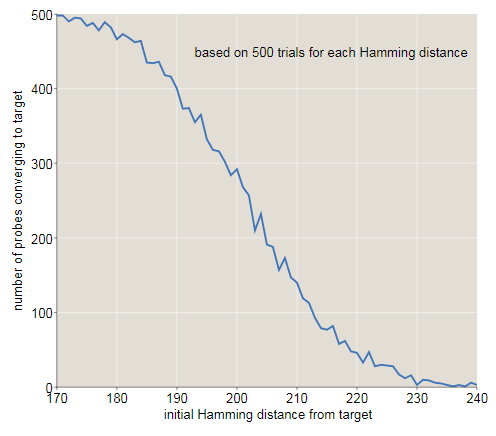
Способность воссоздания воспоминаний из частичной информации — знакомый всем элемент человеческой жизни. Вы замечаете актёра в телешоу, и понимаете, что видели его раньше, но не помните, где. Через несколько минут до вас доходит: это мистер Бейтс из «Аббатства Даунтон», но без костюма дворецкого. Встреча выпускников старшей школы: глядя плотного лысеющего джентльмена на другом конце комнаты, сможете ли вы узнать в нём друга, которого знали только как подростка в спортивных шортах? Иногда на заполнение пробелов требуются длительные усилия. Я уже писал о собственном необъяснимом «слепом пятне» в памяти о выращивании глициний, которые я смог назвать только после терпеливого перелистывания каталога поддельных запахов: гортензии, вербены, форзиции.
Может ли наше умение восстанавливать воспоминания из неполных или зашумлённых входных данных работать подобно рекурсивному процессу вспоминания высокоразмерных векторов? Это было бы привлекательной гипотезой, однако есть причины относиться к ней настороженно. Например, мозг, похоже, способен извлекать смысл из гораздо более скудных сигналов. Мне не нужно прослушивать четыре пятых «Пятой симфонии», чтобы опознать её, достаточно первых четырёх нот. Мелькнувший в деревьях цвет мгновенно заставляет вспомнить соответствующие виды птиц — кардинала, голубую сойку, щегла. Малейшее дуновение с запахом меловой пыли переносит меня обратно в усыпляющий душный класс, в котором я полдня рисовал за партой. Такие воспоминания вызываются крошечными долями представляющей их информации, гораздо меньшими, чем 80 процентов.
Канерва упоминает ещё одну особенность человеческой памяти, которую можно смоделировать при помощи SDM: феномен «вертится на кончике языка», суть которого в том, что вы знаете, что что-то знаете, хотя и не можете сразу же назвать это. Это ощущение довольно загадочно: если вы не можете найти то, что искали, как можно знать, что оно всё такие хранится в мозгу? Рекурсивный процесс вспоминания из SDM предлагает нам возможный ответ. Когда последовательные паттерны, извлекаемые из памяти, становится постоянно ближе друг к другу, мы резонно можем быть уверены в том, что они сойдутся к цели ещё до того, как они до неё добрались.
В попытках извлечения упорного факта из памяти многие люди обнаруживают, что постоянно стучать в одну и ту же дверь — не самая мудрая стратегия. Вместо того, чтобы требовать немедленных ответов — командовать своим мозгом — часто лучше отложить задачу в сторону, прогуляться, возможно, вздремнуть; ответ может прийти, как будто он был незванным. Можно ли объяснить это наблюдение SDM-моделью? Возможно, по крайней мере, частично. Если последовательность вспоминаемых паттернов не сходится, то дальнейшее её исследование может оказаться бесплодным. Если начать заново с соседней точки в пространстве памяти, то можно прийти к более хорошему результату. Но тут есть загадка: как найти новую отправную точку с более хорошими перспективами? Можно подумать, что достаточно просто случайным образом заменить несколько битов во входном паттерне и надеяться, что в результате он окажется ближе к цели, но вероятность этого мала. Если вектор находится в битах от цели, то битов уже верны (но мы не знаем, какие из бит); при любом случайном изменении мы имеем вероятность в не приблизиться, а уйти ещё дальше. Чтобы добиться прогресса, нужно знать, в каком направлении двигаться, а в -мерном пространстве это сложный вопрос.
Один из аспектов архитектуры SDM заключается в том, что она, похоже, соответствует эффекту повторения или повторного прослушивания для памяти. Если несколько раз повторить стихотворение или практиковаться в исполнении музыкального произведения, то можно ожидать, что в будущем вы запомните его легче. Вычислительная модель должна демонстрировать аналогичный эффект тренировки. Но в традиционной компьютерной памяти это невозможно: нет никаких преимуществ в перезаписи одного и того же значения несколько раз по одному и тому же адресу. В SDM же, напротив, каждое повторение паттерна добавляет ещё одну копию ко всем твёрдым ячейкам в пределах круга доступа паттерна. В результате возникает меньше влияния от пересекающихся паттернов, а критический радиус вспоминания увеличивается. Эффект оказывает значительное влияние: при записи в память единственной копии паттерна критический радиус увеличивается с примерно бит до более чем .
Аналогично, воспроизведение одного паттерна может усложнить восстановление остальных. Это напоминает забывание, когда активно запечатляемый паттерн заполняет своих соседей и захватывает часть их территории. Этот эффект тоже значительно влияет на SDM, настолько, что это даже кажется нереальным. Похоже, что вектор, сохранённый восемь или десять раз, монополизирует бОльшую часть памяти; он становится одержимостью, ответом на все вопросы.
Важное преимуещство разреженной распределённой памяти заключается в её устойчивости к аппаратным сбоям или ошибкам. Я был бы расстроен, если бы утеря единственного нейрона в моём мозгу оставляла дыру в памяти, и я не мог бы распознать букву g или вспомнить, как завязывать шнурки. SDM не страдает от подобной хрупкости. Когда у каждого хранящегося паттерна есть тысяча копий, ни одно место не является принципиальным. И в самом деле, можно стереть всю информацию, хранящуюся в 60 процентах твёрдых ячеек, и всё равно иметь идеальное вспоминание , если считать, что мы передаём в качестве сигнала абсолютно точный адрес. При частичных сигналах критический радиус сжимается при увеличении потерянных мест. После уничтожения 60 процентов мест критический радиус сжимается с бит до примерно бит. После уничтожения 80 процентов мест память оказывается серьёзно повреждена, но не уничтожена.
А как насчёт витания в облаках? Можем ли мы праздно блуждать по лугам разреженной распределённой памяти, по счастливой случайности перепрыгивая от одного хранимого паттерна к другому? Я вернусь к этому вопросу.
БОльшая часть изложенного выше написана несколько недель назад. В то время я читал о различных конкурирующих теориях памяти и обсуждал их достоинства с коллегами из Института Саймонса. Я записал свои мысли на эту тему, но отложил их публикацию из-за неотступных сомнений: правильно ли я понял математику разреженной распределённой памяти? Теперь я рад, что не торопился.
Программа «Мозг и вычисления» завершилась в мае. Её участники разъехались: я вернулся в Новую Англию, где шалфей и розмарин — это небольшие горшечные растения, а не нависающие над дорожками пышные кусты. Мои утренние прогулки к кампусу в Беркли, ежедневные возможности поразмыслить о природе памяти и обучения, стали «энграммами», хранящимися где-то в моей голове (однако я всё ещё не знаю, где их искать).
Однако я не отказался от своих поисков. После отъезда из Беркли я продолжил читать о теориях памяти. Также я писал программы для изучения разреженной распределённой памяти Пентти Канерва и его более пространных идей «гиперпространственных вычислений». Даже если этому проекту не удастся открыть мне секреты человеческой памяти, он определённо научит меня чему-то о математическом и вычислительном искусстве навигации в высокоразмерных пространствах.
На схеме ниже показан «правильный» способ реализации SDM, насколько я её понимаю. Основной элемент — это перекрёстная матрица, в которой строки соответствуют твёрдым ячейкам памяти, а столбцы переносят сигналы, имитирующие отдельные биты входного вектора. В канонической памяти миллион строк, каждой из которых случайным образом назначен -битный адрес, и столбцов; эта демонстрационная версия состоит из 20 строк и 8 столбцов.
![[Перевод] 1000-мерный куб: можно ли сегодня создать вычислительную модель человеческой памяти? [Перевод] 1000-мерный куб: можно ли сегодня создать вычислительную модель человеческой памяти?](https://habrastorage.org/webt/hm/bf/hq/hmbfhq9wergzhrrb1fskxsurpsk.png)
Проиллюстрированный на схеме процесс заключается в сохранении одного входного вектора в пустую память. Восемь входных битов одновременно сравниваются со всеми 20 адресами твёрдых ячеек. Когда входной бит и бит адреса совпадают — ноль с нулём или единица с единицей — мы ставим на пересечении столбца и строки точку. Затем мы считаем количество точек в каждой строке, и если количество равно или превышает пороговое значение, то мы записываем входной вектор в регистр, связанный с этой строкой (синие поля). В нашем примере пороговое значение равно 5, и в 8 из 20 адресов есть не менее 5 совпадений. В -битной памяти пороговое значение будет равно , а выбраны окажутся всего около одной тысячной всех регистров.
Волшебство этой архитектуры в том, что все сравнения битов — а в канонической модели их миллиард — происходят одновременно. Поэтому время доступа для чтения и записи не зависит от количества твёрдых ячеек и может быть очень малым. Такая компоновка общего типа, известная как ассоциативная память или память с адресацией по содержимому, используется в некоторых вычислительных областях, таких как включение детекторов частиц в Большом адронном коллайдере и передача пакетов через маршрутизаторы в Интернете. И схему цепи можно связать с определёнными структурами мозга. Канерва указывает на то, что на такую матрицу очень похож мозжечок. Строки — это плоские, веерообразные клетки Пуркинье, собранные наподобие страниц книги; столбцы — это параллельные волокна, протянувшиеся по всем клеткам Пуркинье. (Однако мозжечок — это не область мозга млекопитающих, где, как считается, находится когнитивная память.)
Было бы здорово построить SDM-симуляцию на основе этой перекрёстной архитектуры; к сожалению, я не знаю, как реализовать её на имеющемся в моём распоряжении компьютерном оборудовании. В традиционном процессоре нет способов для одновременного сравнения всех входных битов с битами твёрдых ячеек. Вместо этого мне приходится последовательно проходить по миллиону твёрдых ячеек, и в каждом месте сравнивать тысячи пар битов. Это составляет миллион сравнений битов для каждого элемента, сохраняемого или извлекаемого из памяти. Добавьте к этому время на запись или чтение миллиона бит (тысячи копий -битного вектора), и у вас получится довольно медленный процесс. Вот код для сохранения вектора:
function store(v::BitVector) for loc in SDM if hamming_distance(v, loc.address) <= r write_to_register!(loc.register, v) end end endЭтой реализации требуется около часа на инвентаризацию памяти с запомненными паттернами. (Полная программа в виде Jupyter notebook выложена на GitHub.)
Существует ли более хороший алгоритм для симуляции SDM на обычном «железе»? Одна из возможных стратегий позволяет избежать повторяющегося поиска набора твёрдых ячеек в пределах круга доступа заданного вектора; вместо этого, когда вектор впервые записывается в память, программа сохраняет указатель на каждое из тысячи или около того мест, в которых он хранится. В дальнейшем при любой ссылке на тот же вектор программа может проследовать по сохранённых указателей, а не сканировать весь массив из миллиона твёрдых ячеек. Цена этой схемы с кэшированием заключается в необходимости хранения всех этих указателей — в канонической SDM их миллионов. Это вполне реально, и может стоить того, если вы хотите хранить и извлекать только точные, известные значения. Но подумайте, что произойдёт в ответ на приблизительный запрос памяти с рекурсивным вспоминанием и и , и так далее. Ни одно из этих промежуточных значений не будет найдено в кэше, поэтому всё равно потребуется полное сканирование всех твёрдых ячеек.
Возможно, здесь есть и более хитрая возможность срезать путь. В недавней обзорной статье "Approximate Nearest Neighbor Search in High Dimensions" Александра Андони, Петра Индыка и Ильи Разенштейна упоминается интригующая техника под названием locality sensitive hashing (хэширование с учётом локальности), но пока я не совсем понимаю, как адаптировать её под задачу SDM.
Способность восстанавливать воспоминания по частичным сигналам — это до боли человеческая особенность вычислительной модели. Возможно, её можно расширить для получения правдоподобного механизма праздного блуждания по чертогам разума, при котором одна мысль приводит к следующей.
Сначала я думал, что знаю, как это может работать. Хранящийся в SDM паттерн создаёт вокруг себя область притяжения, в которой любое рекурсивное исследование памяти начиная с критического радиуса сойдётся к . При таких аттракторах я могу представить, как они разбивают пространство памяти на матрицу отдельных модулей наподобие высокоразмерной пены из мыльных пузырей. Область для каждого хранящегося элемента занимает отдельный объём, окружённый со всех сторон другими областями и упирающийся в них, с чёткими границами между соседними доменами. В поддержку такого суждения я могу заметить, что средний радиус области притяжения при добавлении в память нового содержимого сжимается, как если бы пузыри сжимались из-за скученности.
Такое видение процессов внутри SDM предполагает наличие простого способа перемещения от одного домена в другой: нужно случайным образом переключить достаточное количество бит вектора, чтобы переместить его из пределов текущей области притяжения в соседнюю, а затем применить алгоритм рекурсивного вспоминания. Повторение этой процедуры сгенерирует случайный обход множества тем, хранящихся в памяти.
Единственная проблема в том, что такой подход не работает. Если проверить его, то он и в самом деле будет бесцельно блуждать по мерной решётке, но мы никогда не найдём ничего, хранящегося там. Весь план основан на ошибочном интуитивном понимании геометрии SDM. Хранящиеся векторы с их областями притяжения не упакованы плотно подобно мыльным пузырям; напротив, они являются изолированными галактиками, висящими в обширной и свободной вселенной, разделённые огромными участками пустого пространства между ними. Краткие вычисления показывают нам истинную природу ситуации. В канонической модели определяющий область притяжения критический радиус приблизительно равен . Объём отдельной области, измеренный как количество находящихся внутри векторов, равен
что примерно равно . Поэтому все областей занимают объём . Это большое число, но оно всё равно является крошечной долей -мерного куба. Среди всех вершин куба только из лежит в пределах 200 бит сохранённого паттерна. Можно вечно блуждать, так и не наткнувшись ни на одну из этих областей.
(Вечно? Ох, ну да, может быть и не вечно. Поскольку гиперкуб — это конечная структура, любой путь через него рано или поздно обязан стать периодичным, или попав в фиксированную точку, из которой никогда никогда не выйдет, или заблудившись в повторяющемся цикле. Хранящиеся векторы являются фиксированными точками, кроме того, существует множество других фиксированных точек, не соответствующих никакому значимому паттерну. Как бы то ни было, во всех моих экспериментах с программами SDM мне ни разу не удавалось «случайно» попасть в сохранённый паттерн.)
Пытаясь спасти эту неудачную идею, я провёл ещё несколько экспериментов. В одном случае я произвольно сохранял несколько связанных концепций в соседние адреса («соседние», то есть
в пределах 200 или 300 бит). Возможно, в пределах этого кластера я смогу беззаботно перескакивать из точки в точку. Но на самом деле весь кластер сгущается в одну большую область притяжения для центрального паттерна, который становится чёрной дырой, всасывающей в себя всех своих компаньонов. Также я попробовал поиграться со значением (радиусом круга доступа для всех операций считывания и записи). В канонической модели . Я подумал, что запись в чуть меньший круг или считывание из чуть большего круга оставит достаточно пространства для случайности в результатах, но эта надежда тоже не оправдалась.
Все эти попытки основывались на неправильном понимании высокоразмерных пространств векторов. Попытка нахождения кластеров соседних значений в гиперкубе безнадёжна; хранимые паттерны слишком разнесены по объёму. Произвольное создание плотных кластеров тоже бессмысленно, потому что это разрушает само то свойство, делающее систему интересной — способность сходиться к хранящемуся элементу из любой точки окружающей его области притяжения. Если мы хотим создать алгоритм витания в облаках для SDM, то необходимо придумать какой-то другой способ.
В поисках альтернативного механизма потока сознания можно попробовать добавить в мир разреженной распределённой памяти немного теории графов. Тогда мы сможем сделать шаг назад, обратно к исходной идее умственных блужданий в виде случайного обхода графа или сети. Ключевой элемент для встраивания таких графов в SDM оказывается знакомым нам инструментом: оператором исключающего ИЛИ.
Как сказано выше, расстояние Хэмминга между двумя векторами вычисляется взятием их побитового XOR и подсчётом в получившемся результате единиц. Но операция XOR даёт не просто расстояние между двумя векторами, но и другую информацию; она также определяет ориентацию или направление соединяющей их линии. В частности, операция даёт вектор, перечисляющий биты, которые нужно изменить для преобразования в и наоборот. Также можно воспринимать и в векторе XOR как последовательность направлений, по которым нужно следовать для отслеживания пути от до .
XOR всегда была моей самой любимой из всех булевых функций. Это разностный оператор, но в отличие от вычитания, XOR симметричен: . Более того, XOR является своей собственной обратной функцией. Эту концепцию легко понять при помощи функций с единственным аргументом: является собственной обратной функцией, если , то есть после применения функции дважды мы можем вернуться к тому, с чего начали. Для функции с двумя аргументами, таких как XOR, ситуация сложнее, но по-прежнему истинно то, что выполнение одинакового действия дважды восстанавливает исходное состояние. В частности, если , то и . Три вектора — , и — создают крошечную замкнутую вселенную. К любой паре из них можно применить оператор XOR и получить третий элемент множества. Ниже показана моя попытка проиллюстрировать эту идею. Каждый квадрат имитирует -битный вектор, выстроенных как таблица 100 x 100 из светлых и тёмных пикселей. Три паттерна кажутся случайными и независимыми, но на самом деле каждая панель является XOR двух других. Например, в самом левом квадрате каждый красный пиксель соответствует или зелёному, или синему, но никогда обоим.

Свойство самоинвертируемости подсказывает нам новый способ упорядочивания информации в SDM. Допустим, слово butterfly и его французский аналог papillon хранятся в произвольных, случайных векторах. Они не будут близки друг к другу; расстояние между ними с большой вероятностью примерно равна 500 битам. Теперь мы вычисляем XOR этих векторов butterfly papillon; результатом является ещё один вектор, который также можно сохранить в SDM. Этот новый вектор кодирует связь английский-французский. Теперь у нас есть инструмент для перевода. Имея вектор для butterfly, мы выполняем для него XOR с вектором английский-французский и получаем papillon. Тот же трюк работает и в обратном направлении.
Эта пара слов и связь между ними формируют ядро семантической сети. Давайте немного увеличим её. Мы можем сохранить в произвольном адресе слово caterpillar, а затем вычислить butterfly caterpillar и назвать эту новую связь взрослый-юный. Как по-французски называется caterpillar? Гусеница по-французски — это chenille. Мы добавляем этот факт в сеть, сохраняя chenille по адресу caterpillar English-French. Теперь настало время волшебства: если мы возьмём papillon chenille, то узнаем, что эти слова связаны соотношением взрослый-юный, даже несмотря на то, что явным образом этого не указывали. Это ограничение накладывается самой геометрией конструкции.
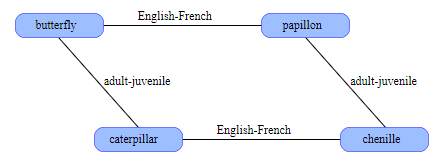
Граф можно расширять и дальше, добавляя больше англо-французских родственных слов (dog-chien, horse-cheval) или больше пар «взрослый-юный»: (dog-puppy, tree-sapling). Можно также исследовать множество других связей: синонимы, антонимы, сиблинги, причина-следствие, хищник-жертва и так далее. Существует также отличный способ соединения множества событий в хронологическую последовательность простым выполнением XOR для адресов предшественника и последователя узла.
Способ соединения концепций через XOR — это гибрид геометрии и теории графов. В математической теории обычных графов расстояния и направления несущественны; единственное, что важно — наличие или отсутствие соединяющих рёбер между узлами. С другой стороны, в SDM представляющее связь между узлами ребро является вектором конечной длины и направленности в -мерном пространстве. При заданном узле и связи операция XOR «привязывает» этот узел к конкретной позиции где-то в другом месте гиперкуба. Получающаяся структура абсолютно жёсткая — мы не можем переместить узел, не изменив все связи, в которых он участвует. В случае с бабочками и гусеницами конфигурация из четырёх узлов неизбежно оказывается параллелограммом, где пары на противоположных сторонах имеют одинаковую длину и направленность.
Ещё одной уникальной характеристикой связанного операцией XOR графа является то, что узлы и рёбра имеют абсолютно одинаковое представление. В большинстве компьютерных реализаций идей из теории графов, эти две сущности очень отличаются; узел может быть списком атрибутов, а ребро — парой указателей на соединяемые им узлы. В SDM и узлы, и рёбра являются просто высокоразмерными векторами, которые можно хранить в одинаковом формате.
При использовании в качестве модели человеческой памяти XOR-привязки даёт нам возможность соединения любых двух концепций через любую связь, которую мы можем придумать. Множество связей в реальном мире несимметрично; они не имеют свойства самоинвертируемости, которое есть у XOR. Вектор XOR может объявлять, что Эдвард и Виктория являются родителем и ребёнком, но не сообщает, кто из них кто. Хуже того, вектор XOR соединяет ровно два узла и никогда больше, поэтому родитель нескольких детей ставит нас в неприятное положение. Ещё одна сложность заключается в сохранении целостности всех ветвей большого графа друг с другом. Мы не можем просто произвольно добавлять узлы и рёбра; их необходимо присоединить к графу в правильном порядке. Вставка стадии куколки между бабочкой и гусеницей потребует переписывания большей части схемы; придётся переместить несколько узлов в новые места внутри гиперкуба и пересчитать соединяющие их векторы связей, при этом сделав так, чтобы каждое изменение на стороне английского языка правильно отразилось и на французской.
Некоторые из этих проблем решаются в другой технике на основе XOR, которую Канерва называет бандлингом (bundling). Идея заключается в создании некой базы данных для хранения пар «атрибут-значение». Запись для книги может иметь такие атрибуты, как author, title и publisher, каждое из которых спарено с соответствующим значением. Первый этап бандлинга данных заключается отдельном XOR каждой пары «атрибут-значение». Затем векторы, полученные из этих операций, комбинируются для создания единого суммарного вектора с помощью того же алгоритма, описанного выше для хранения нескольких векторов в твёрдой ячейке SDM. Выполняя XOR имени атрибута с этим комбинированным вектором, мы получаем аппроксимацию соответствующего значения, достаточно близкое для того, чтобы определить его методом рекурсивного вспоминания. В экспериментах с канонической моделью я выяснил, что -битный вектор может хранить шесть или семь пар «атрибут-значение» без особого риска путаницы.
Привязка и бандлинг не упоминаются в книге Канерва 1988 года, но он подробно рассказывает о них в более новых статьях. (См. ниже раздел «Дополнительное чтение».) Он указывает на то, что с этими двумя операторами множество высокоразмерных векторов приобретает структуру алгебраического поля, или, по крайней мере, приближения к полю. Канонический пример поля — это множество вещественных чисел вместо с операциями сложения и умножения, а также их обратных операторов. Вещественные числа создают под этими операциями замкнутое множество: сложение, вычитание, умножение или деление любых двух вещественных чисел даёт ещё одно вещественное число (за исключением деления на ноль, которое всегда является джокером в колоде). Аналогично, множество двоичных векторов является замкнутым для связывания и бандлинга, за исключением того, что иногда для восстановления члена множества результат, извлечённых из бандлинг-вектора нужно «очистить» процессом рекурсивного вспоминания.
Могут ли связывание и бандлинг помочь нам в получении алгоритма витания в облаках? Они дают нам базовые инструменты для навигации по семантическому графу, в том числе возможность выполнения случайного обхода. Начиная с любого узла в связанном XOR графе, алгоритм случайного обхода выбирает среди всех связей, имеющихся в этом ужле. Случайный выбор вектора связи и выполнение XOR этого вектора с адресом узла приводит нас к другому узлу, где процедуру можно повторить. Аналогичным образом, в парах «атрибут-значение» бандлинга случайно выбранный атрибут вызывает соответствующее значение, которое становится следующим исследуемым узлом.
Но как алгоритм узнаёт, какие связи или какие алгоритмы доступны для выбора? Связи и атрибуты представлены в форме векторов и хранятся в памяти как и любые другие объекты, поэтому не существует очевидных способов получения этих векторов, если только не знать, какие они на самом деле. Мы не можем сказать памяти «покажи мне все связи». Мы можем только показать паттерн и спросить «есть ли такой вектор? видела ли ты что-то подобное?»
В традиционной компьютерной памяти мы можем получить дамп памяти: пройтись по всем адресам и вывести значение, найденное в каждом месте. Но для распределённой памяти такой процедуры нет. Мне этот удручающий факт дался с трудом. При построении вычислительной модели SDM мне удалось добиться достаточно хорошей работы, чтобы получить возможность хранить в памяти несколько тысяч случайно сгенерированных паттернов. Но я не мог извлекать их, потому что не знал, что запрашивать. Решение заключалось в создании отдельного списка за пределами самой SDM, в который бы записывалось всё, что я сохраняю. Но предположение о том, что мозг хранил бы и память, и индекс этой памяти, кажется надуманным. Почему не использовать просто индекс, ведь это намного проще?
Ввиду этого ограничения похоже, что разреженная распределённая память оборудована для обслуживания чувств, но не воображения. Она может распознавать знакомые паттерны и сохранять новые, которые будут распознаваться при следующих встречах даже из частичных или повреждённых сигналов. Благодаря связыванию или бандлингу память также может отслеживать связи между парами сохранённых элементов. Но всё, что записывается в память, может быть извлечено только при передаче подходящего сигнала.

Когда я смотрю на постер «Выпускника», то вижу Дастина Хоффмана, смотрящего на ногу Энн Бэнкрофт в чулке. Этот визуальный стимул возбуждает подмножества нейронов в коре головного мозга, соответствующие моим воспоминаниям об актёрах, персонажах, сюжете, саундтреке и 1967 годе. Всю эту активность мозга можно объяснить архитектурой памяти SDM, если мы допустим, что подмножества нейронов можно представить в некой абстрактной форме как длинные случайные двоичные векторы. Но нельзя так же просто объяснить то, что я могу вызвать в мозгу все те же ощущения, не видя этой картинки. Как я извлекаю конкретно эти длинные случайные последовательности из огромного переплетения векторов, не зная точно, где они находятся?
На этом моё долгое путешествие заканчивается — нотой сомнения и разочарования. Вряд ли вас удивляет, что мне не удалось добраться до самой сути. Это очень сложная тема.
В самый первый день программы «Мозг и вычисления» в Институте Саймонса Джефф Лихтман, работающий над трассировкой схемы коммутаций в мозгу мышей, задал вопрос: достигли ли уже нейронауки момента Уотсона-Крика? В молекулярной генетике мы достигли точки, в которой смогли излечь из живой клетки цепь ДНК и считать многие из сообщений в ней. Мы даже можем записывать собственные сообщения и вставлять их обратно в организм. Аналогичной способностью в нейронауках было бы исследование ткани мозга и считывание хранящейся в ней информации — знаний, воспоминаний, взглядов на мир. Возможно, мы могли бы даже записывать информацию непосредственно в мозг.
Наука даже близко не подошла к достижению этой цели, к радости многих. В том числе и меня: я не хочу, чтобы мои мысли были высосаны из головы через электроды или пипетки и заменены на #fakenews. Однако, мне на самом деле хочется знать, как работает мозг.
Программа Института Саймонса ослепила меня недавними успехами нейронаук, но также дала мне понять, что один из самых серьёзных вопросов остаётся неотвеченным. Проекты Лихтманна и других по коннектомике создают подробную карту из миллионов нейронов и их связей. Новые техники записи позволяют нам слушать сигналы, испускаемые отдельными нейроцитами и следовать за волнами возбуждения по широким областям мозга. У нас есть достаточно всеобъемлющий каталог типов нейронов и мы многое знаем об их физиологии и биохимии. Всё это впечатляет, но загадки всё ещё есть. Мы можем записывать нейросигналы, но по большей части мы не знаем, что они означают. Мы не знаем, как кодируется и хранится информация в мозгу. Это похоже на попытки понять принципиальную схему цифрового компьютера без знания двоичной арифметики и булевой логики.
Модель разреженной распределённой памяти Пентти Канерва — одна из попыток заполнения некоторых таких пробелов. Это не единственная такая попытка. Более известной альтернативой является подход Джона Хопфилда — концепция нейронной сети как динамической системы, принимающей форму минимизирующего энергию аттрактора. У этих двух идей есть общие базовые принципы: информация рассеяна по огромному количеству нейронов и закодирована в форме, неочевидной для внешнего наблюдателя, даже он получит доступ ко всем нейронам и проходящим по ним сигналам. Подобные схемы, по сути являющиеся математическими и вычислительными, концептуально находятся посередине между высокоуровневой психологией и низкоуровневой нейронной инженерией. В этом слое располагается значение.
Дополнительное чтение
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences 79(8):2554–2558.
Kanerva, Pentti. 1988. Sparse Distributed Memory. Cambridge, Mass.: MIT Press.
Kanerva, Pentti. 1996. Binary spatter-coding of ordered K-tuples. In C. von der Malsburg, W. von Seelen, J. C. Vorbruggen and B. Sendhoff, eds. Artificial Neural Networks—ICANN 96 Proceedings, pp. 869–873. Berlin: Springer.
Kanerva, Pentti. 2000. Large patterns make great symbols: An example of learning from example. In S. Wermter and R. Sun, eds. Hybrid Neural Systems, pp. 194–203. Heidelberg: Springer. PDF
Kanerva, Pentti. 2009. Hyperdimensional computing: An introduction to computing in distributed representation with high-dimensional random vectors. Cognitive Computation 1(2):139–159. PDF
Kanerva, Pentti. 2010. What we mean when we say “What’s the Dollar of Mexico?”: Prototypes and mapping in concept space. Report FS-10-08-006, AAAI Fall Symposium on Quantum Informatics for Cognitive, Social, and Semantic Processes. PDF
Kanerva, Pentti. 2014. Computing with 10,000-bit words. Fifty-second Annual Allerton Conference, University of Illinois at Urbana-Champagne, October 2014. PDF
Plate, Tony. 1995. Holographic reduced representations. IEEE Transactions on Neural Networks 6(3):623–641. PDF
Plate, Tony A. 2003. Holographic Reduced Representation: Distributed Representation of Cognitive Structure. Stanford, CA: CSLI Publications.
Источник


