Понимаю, что тема избитая и очень неблагодарная, как поиски вечного двигателя и свободной энергии. Но всё-таки попробую ещё раз не судите строго.
Для того чтобы, начать движение нужно от чего оттолкнуться, это факт. Законы Ньютона знают все. Поэтому пока не разорвется связь между телами, движения не будет. На этом простом основании можно сказать, что получить безопорное движение на инерциоидах невозможно. Пока есть связь между телами жесткая или мягкая общая точка центра масс никуда не сдвинется. Поэтому двигаться можно только отбросив что-то (некое рабочее тело). разорвав с ним связь. Тогда остается только что-то отбросить, но в то же время вернуть «это» что-то обратно и снова от него оттолкнуться. Остается играть векторами. Решение есть. Здесь видео короткой лекции. Но это уже немного устаревшая информация. (Можно пропустить).
Следующим шагом я хочу предложить частный случай моей гипотезы. Заменить удары шариков об “углы” (см Видео выше) на круговое движение. Это гораздо проще, но принцип остается тот-же. Хотя с «углами» нагляднее и проще объяснять.
И так, мы имеем замкнутый объем в форме окружности. Внутри этого объема с постоянной скоростью V движется шар.
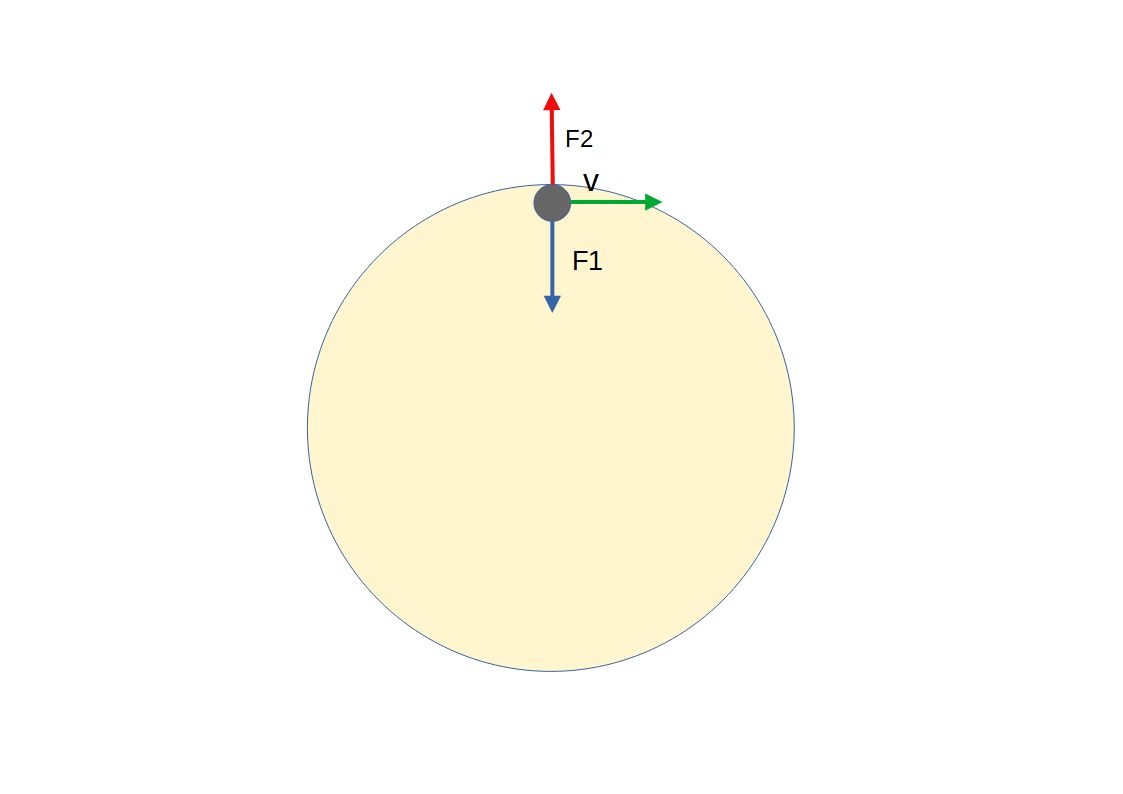
Согласно законам механики на шар действуют центростремительная сила F1 которая заставляет шар двигаться по окружности и равная, но противостоящая ей центробежная сила F2, это сила с которой шар давит на стенку. Рассмотрим эти силы во времени. Если бы шар двигался с постоянной скоростью, то эти силы оставались бы постоянными и естественно вся система оставалась бы в состоянии покоя. Мы имели бы такую картину
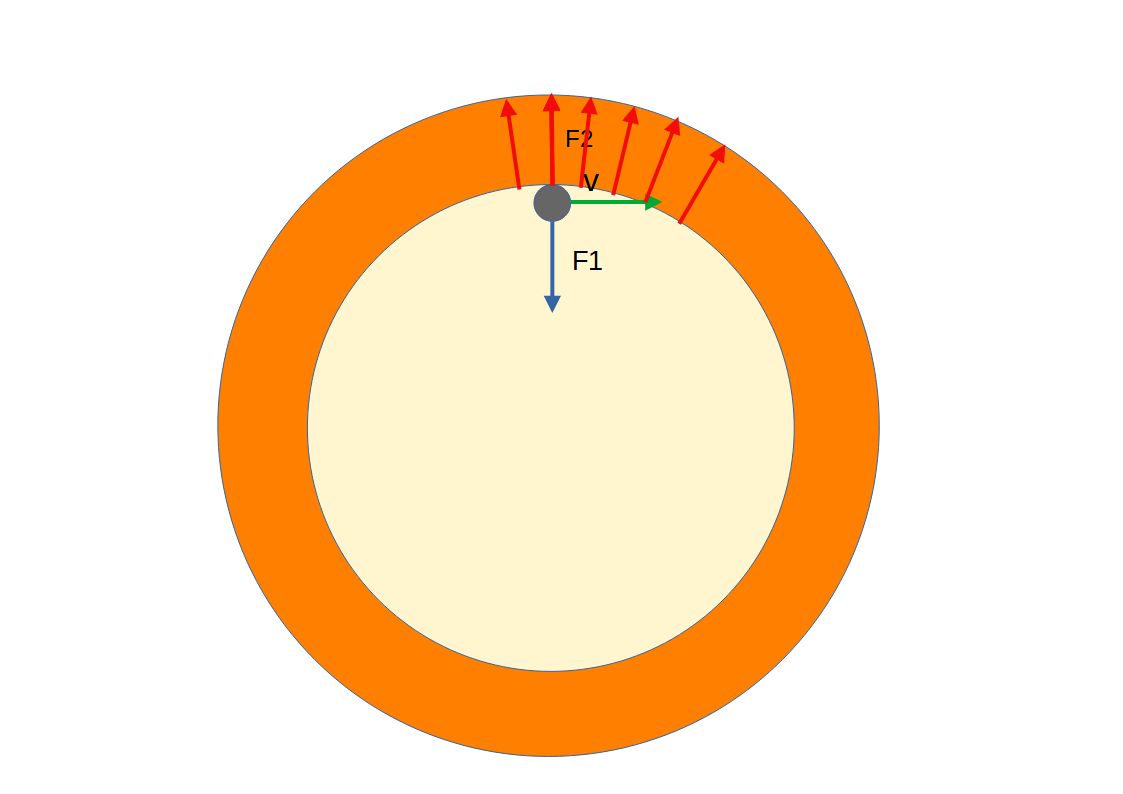
На рисунке показаны векторы, действующие на систему в каждый момент времени по мере движения шарика по своей траектории. Но так как шарик у нас катится по инерции, не получая не откуда дополнительных импульсов то учитывая силы трения качения он замедляется а, следовательно, теряет скорость и, следовательно, уменьшаются все силы F1 и F2 что нам очень полезно.
И мы получим такую картину векторов.
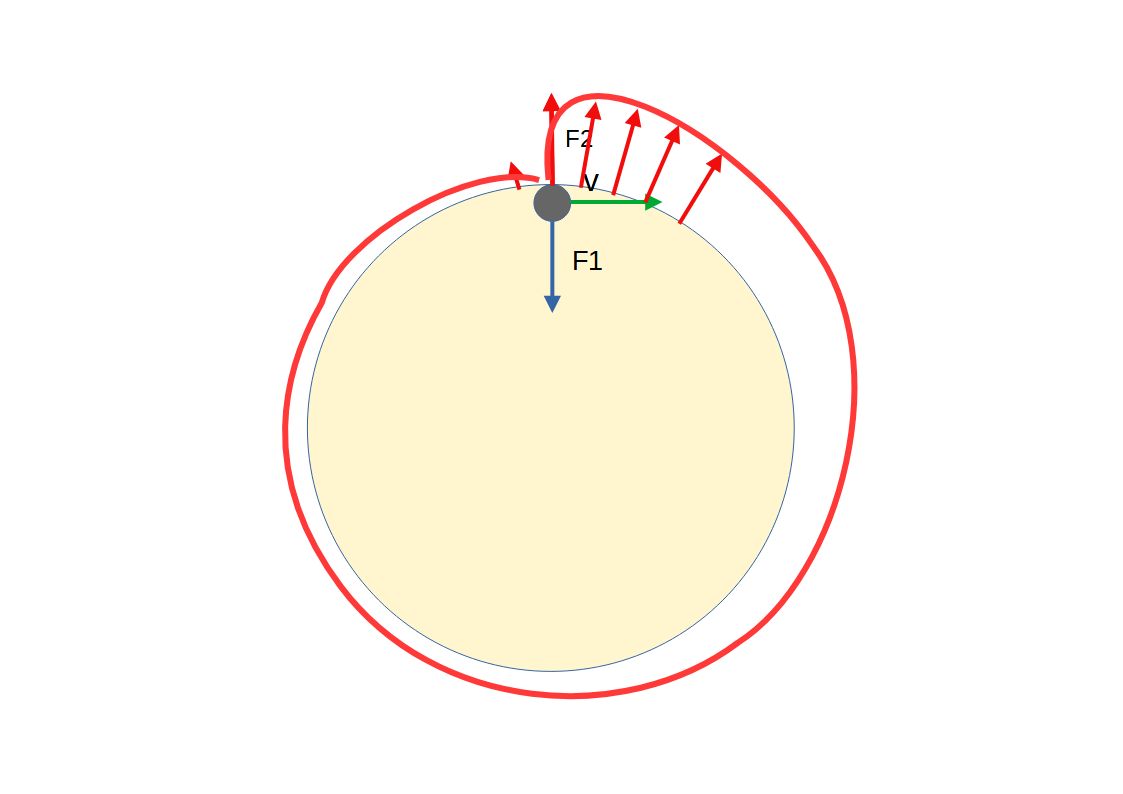
А теперь мы будем ускорять наш шарик каждый раз в тот момент времени, когда он будет проходить верхнюю точку. А так как мы рассматриваем замкнутую систему то мы говорим о том, что сама система отталкивается от шарика.
Тогда мы будем иметь такую картинку.

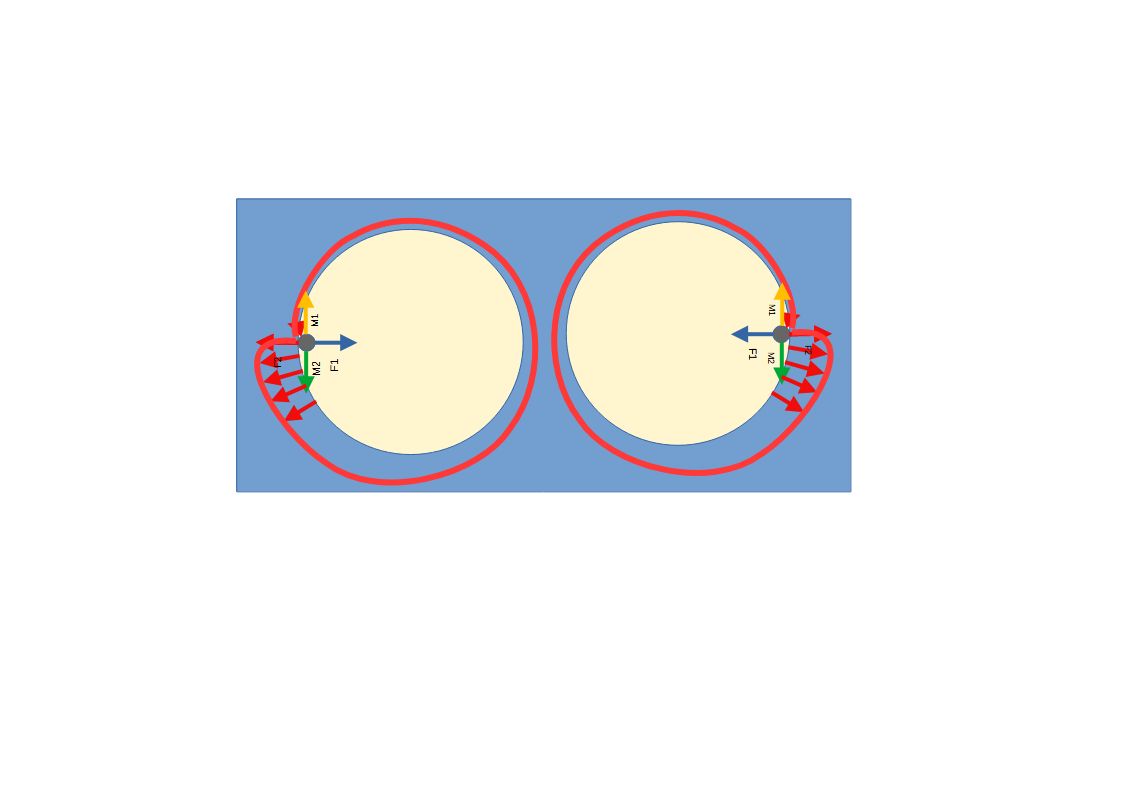
Импульс М1 получает сама система, а импульс М2 получает шарик. Отталкиваясь от шарика, система будет получать некоторый вращательный импульс что будет закручивать её в противоположную сторону. Чтобы уравновесить аппарат сделаем второй экземпляр системы в зеркальном отображении.
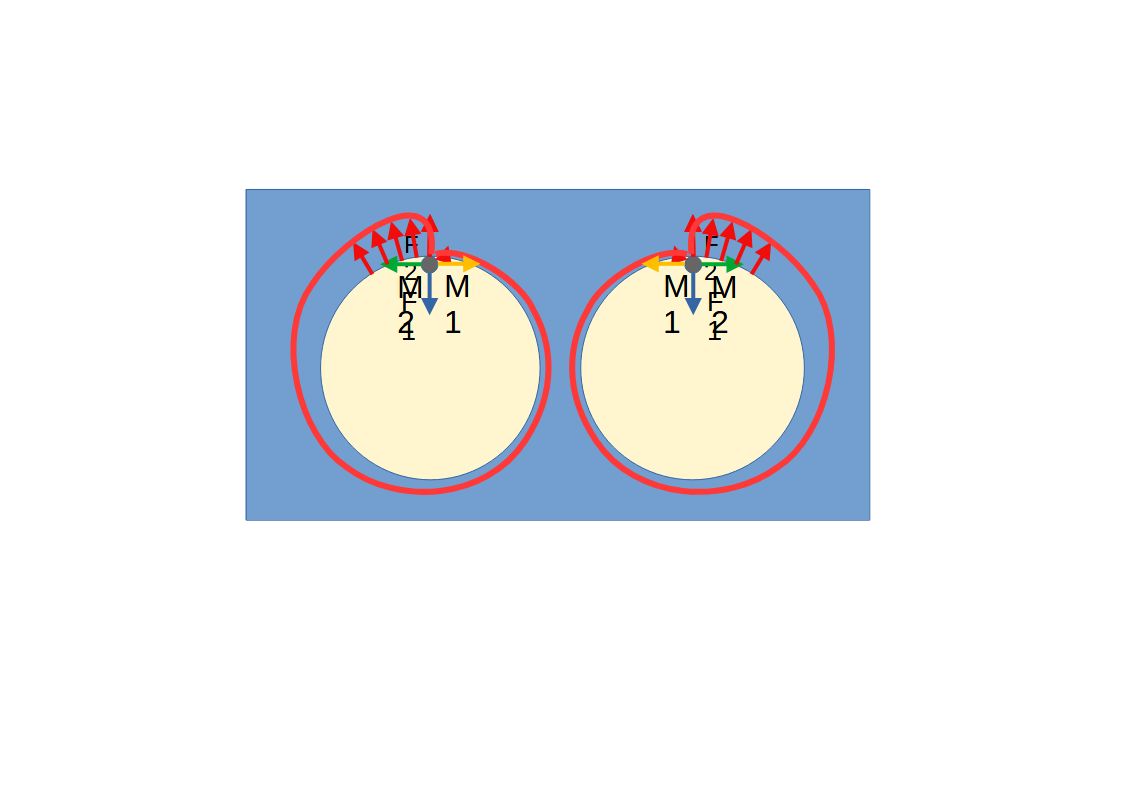
Таким образом импульсы М1 правый и левый будут скомпенсированы. А импульсы М2 будут действовать на шарики зеркально.
Рассмотрим все действующие на систему векторы.

Как видно из рисунка верхние векторы А1 и А2 будут несколько больше нижних B1 и B2, сумма верхних векторов будет вектор А3. Суммой нижних векторов будет вектор B3. Сложив векторы А3 и В3 в остатке мы получим вектор А4 который и будет действовать на систему и заставит её двигаться.
Я позволил себе сделать простенькую математическую модель в симуляторе Phun и модель действительно стала двигаться. Предлагаю видео.
Я так же делал модели так сказать в металле они были далеки от совершенства, но тогда я ещё делал с углами.
И кстати в симуляторе заработала даже такая схема
Мои предыдущие модели как-то слабо ползали. Но теперь после моделирования в симуляторе я понял, как надо делать и в ближайшее время хочу сделать уже реальную модель. Но только хотелось бы предупредить что, в симуляторе я делал в условиях невесомости. Для условий гравитации я буду «крутить» шарики в плоскости земли по понятным соображениям. Хотя может удастся получить вращение в вертикальной плоскости, тогда получится зафиксировать заветную потерю веса. Или, наоборот, увеличение веса (что проще).
Я не смог чисто физически просчитать в цифрах, но если брать симуляцию, то масса шариков составляла примерно четверть от массы всего аппарата. Но там очень низкая скорость движения шариков, зато большая мощность двигателя. Я полагаю если удастся запускать шарики (рабочее тело) с большей скоростью, в виде постоянного потока, то можно будет уменьшить их массу. Чисто теоретически так можно сделать аппарат, который смог бы подниматься в условиях земной гравитации, то тогда понадобиться рабочее тело гораздо большей массы почти в половину всего аппарата, и очень огромная мощность чтобы заставить такую массу двигаться внутри аппарата. Хотя если рабочее тело будет иметь достаточно большую скорость может его и меньше надо будет. К тому же я предлагаю только концепцию движения. Рабочим телом может быть всё что угодно. Например ртуть или поток другого вещества.
Ну и напоследок хотелось бы немного помечтать. Как такие движители позволили бы ускорять космические аппараты до огромных скоростей. Представляете, не нужно за собой таскать цистерны с горючим и окислителем, достаточно иметь ядерный реактор, получать электрическую энергию и разгонять космический аппарат. Путь до марса сократился бы с 8-ми месяцев до 2-х недель. Только начинать тормозить надо будет с полпути где-то. Думаю, что такой двигатель будет гораздо эффективнее какого-нибудь ионного разгонного или EmDrive.
А на современном этапе это могут быть небольшие маневровые двигатели для ориентации в космосе.
Всем успехов и добра! Дерзайте и вы добьетесь успеха.


