Конференции — важная часть науки. И так уж сложилось, что в области компьютерных наук — и в особенности в машинном обучении — они играют более важную роль, чем в остальных научных областях. Существует даже специальный рейтинг конференций, по важности сопоставимый с рейтингом научных журналов для учёных, занимающихся ИИ.
Среди лидеров этого списка (рейтинг A*) самой топовой с точки зрения цитирования по сей день остаётся конференция Neural Information Processing Systems или, сокращённо, NeurIPS, куда ежегодно стремятся попасть многие исследователи. Статьи и доклады проходят там жёсткий отбор — в 2023 году туда было принято лишь 26 процентов статей. Тем приятнее, что на NeurIPS 2023, который прошёл в декабре, учёными Института искусственного интеллекта AIRI было сделано там сразу восемь докладов.
О том, какие результаты представили там наши исследователи, я расскажу в тексте ниже.

Немного истории
NeurIPS имеет давнюю историю, которая берёт своё начало в 1987 году. В этот период возникла идея тесного сотрудничества между исследователями, занимающимися искусственными и биологическими нейронными сетями, поэтому тематика первых лет покрывала широкий спектр вопросов, начиная от психологии и заканчивая теорией информации. Как мы теперь знаем, это было верное направление, поскольку нейронные сети пронизывают всё больше аспектов нашей жизни, и сегодня конференция Neural Information Processing Systems — это престижнейшее мероприятие в первую очередь для специалистов по машинному обучению, искусственному интеллекту и статистике.
Любопытный факт: изначально аббревиатурой конференции было NIPS, но в 2018 году от него решили отказаться в пользу более длинного акронима. Причиной тому стали неполиткорректные ассоциации, которые она вызывала: «nipples» (то есть «соски» с английского) — с одной стороны и «nip» (расистское оскорбление, используемое в отношении японцев) — с другой.
Традиционным местом проведения этой конференции по сей день остаётся северо-американский континент (США и Канада), хотя в 2011 и 2016 годах она проходила в Испании. Пандемия коронавируса внесла свои коррективы в работу этого мероприятия, однако, благодаря ей у учёных появилась возможность представлять свои доклады дистанционно. В 2023 году местом проведения стал Новом Орлеан, а темами года стали обработка естественного языка и большие языковые модели, машинное обучение в естественных науках и экологии, мультиагентное обучение и автономные системы.
Итак, поговорим о том, какими успехами поделились там исследователи из AIRI.
Детектор текстов, сгенерированных ИИ
Наверняка большинство читающих эти строки хоть иногда да использует какую-нибудь языковую модель (например, ChatGPT или его аналог) для рутинной работы с текстами или даже кодом. Задействовать большую языковую модель для написания диплома или курсовой заманчиво, и теперь это головная боль для преподавателей и ВУЗов, которые только-только привыкли к работе антиплагиата. Не могу не отметить в этой связи свежую историю про ChatGPT, который общался за парня с девушками в Tinder.
Проблема волнует также и научные издательства — сегодня при оправке статьи многие журналы разрабатывают специальные политики использования искусственного интеллекта при подготовке статьи. Эта тенденция дошла и до региональных отечественных издательств.
Необходимость в создании ИИ-дискриминаторов стала ясна практически сразу же, как большие языковые модели продемонстрировали свои успехи. Так, например, Open AI — создатели ChatGPT, — осознавая социальные риски, которые создаёт их детище, в январе 2023 года предоставили общий доступ к инструменту AI text classifier, который должен был обнаруживать искусственно-сгенерированные тексты. Уже через полгода его авторы закрыли к нему доступ, сославшись на низкую точность, о чём сообщает заглушка на их сайте. В конечном итоге в среде ML-специалистов стали раздаваться голоса о невозможности создания такого дискриминатора.
Оказалось, что всё не так плохо. Помощь пришла со стороны высшей математики и топологического анализа данных. Если очень упрощённо: текстовые данные можно представить себе в виде точек в некотором многомерном пространстве. Можно предположить, что данные сгруппированы на некоторой сложной поверхности в нём. Проблема в том, что такая поверхность может обладать фрактальными признаками, поэтому для её исследования требуется сложная математика.
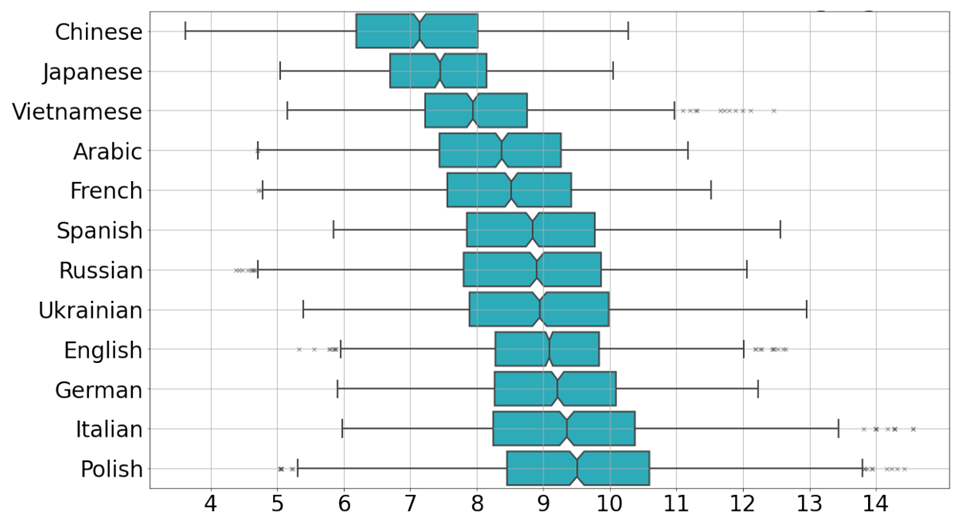
Авторы нового исследования разработали метод определения размерности такой поверхности (исследователи назвали её внутренней размерностью), который опирается на концепцию устойчивых гомологий. Я опущу подробности — их всегда можно найти в научной статье, посвященной разработке, либо в блоге Института. Для нас важно, что эта размерность отличается для человеческого и машинного текстов с высокой степенью достоверности, что можно использовать на практике. Примечательно, что внутренние размерности различны для текстов на разных языках — от 7 ± 1 для китайского до 10 ± 1 для итальянского, — но надёжная дискриминация достигается во всех из них.
Оптимальный транспорт
О диффузионных моделях не слышал только ленивый ИИ-энтузиаст. Если вы из таких, но хотите исправиться, найти информацию о них очень легко даже не покидая Хабр, например, тут. Диффузионки лежат в сердце популярных рисовалок вроде MidJourney, но также применимы к звуку и другим типам данных.
Основной принцип работы диффузионных моделей можно описать простой схемой: вы сначала учите модель тому, как чёткая структура данных (например, картинка) превращается в шум в ходе нескольких актов размывания, а затем просите делать всё наоборот на произвольном шуме. Когда мы пытаемся описать этот процесс на языке статистики, мы говорим о превращении одного распределения вероятностей в другое. Это очень похоже на ситуацию, когда летучие молекулы парфюма равномерно заполнят комнату благодаря процессу диффузии, что и дало название классу моделей.

Если смотреть на этой через призму математики, то каждому распределению можно сопоставить точку в некотором абстрактном пространстве, а процессу диффузии — перемещение или транспорт между ними. Ускорению работы диффузионки способствует нахождению некоторого оптимального транспорта, что выделилось в отдельную задачу машинного обучения.
Этой задачей занимаются спецы из группы «Обучаемый интеллект» AIRI и их коллеги. На NeurIPS 2023 они представили сразу три исследования: теоретически обосновали энтропийный подход к проблеме оптимального транспорта (т.н. Мост Шрёдингера), создали бенчмарк для подобных методов, а также рассмотрели специфическую формулировку проблемы, получившую название экстремального транспорта, в контексте переноса домена. Краткий пересказ сделанного можно найти в блоге (раз, два и три).
Кстати, первая из статей удостоилась статуса «Oral» (то есть, «устный доклад») — его получают только 3% исследований!
Кроме Гаусса
И снова поговорим о диффузионных моделях. А точнее о том, как именно происходит размытие данных.
Традиционно для этого используют свёртку с распределением Гаусса. С одной стороны, точно так же размываются очертания, которые мгновение назад могла принимать упорядоченная структура из молекул в какой-либо среде, например, струйка сиропа в чае. С другой стороны, использование такой формулы позволяет сформулировать задачу на языке цепей Маркова — это когда последовательность случайных событий «помнит» только свой последний шаг.
Проблема тут в том, что для некоторых типов данных такое размытие не очень подходит. Например, если они заданы на сфере или в пределах какой-то сложной фигуры. Для них нужны другие распределения, но пока не существует общей формулировки, которая бы подходила для произвольного их типа.
Важный шаг в эту сторону сделала команда учёных из Европы и России, среди которых есть и сотрудники AIRI. Они пожертвовали самой важной фишкой — марковостью, но зато им удалось обобщить алгоритм диффузионных моделей до целого семейства распределений — экспоненциального семейства, к которому относятся распределения Дирихле, Уишарта, бета-распределение и многие другие. Подробности, как водится, в блоге.
Ансамблированием по трансферному обучению
Следующее исследование посвящено комбинации двух могучих методов: глубоких ансамблей и трансферного обучения.
Глубокие ансамбли — это несколько нейросетей, которые обучаются независимо для одной задачи с различных, случайным образом распределенных стартовых условий. В результате предсказания таких сетей немного отличаются, но их усреднение обычно ближе к оптимальному ответу, чем ответ каждой сети по отдельности — фактически, они исправляют ошибки друг друга.
Трансферное обучение, в свою очередь, решает проблему дефицита качественных и специфичных датасетов. Для этого обучение нейросети делится на предобучение, когда ей скармливается большой, но общий массив данных, и дообучение на малом, но специфичном датасете. Примеры того, как это улучшает работу моделей, можно найти в недавнем посте на Хабре.
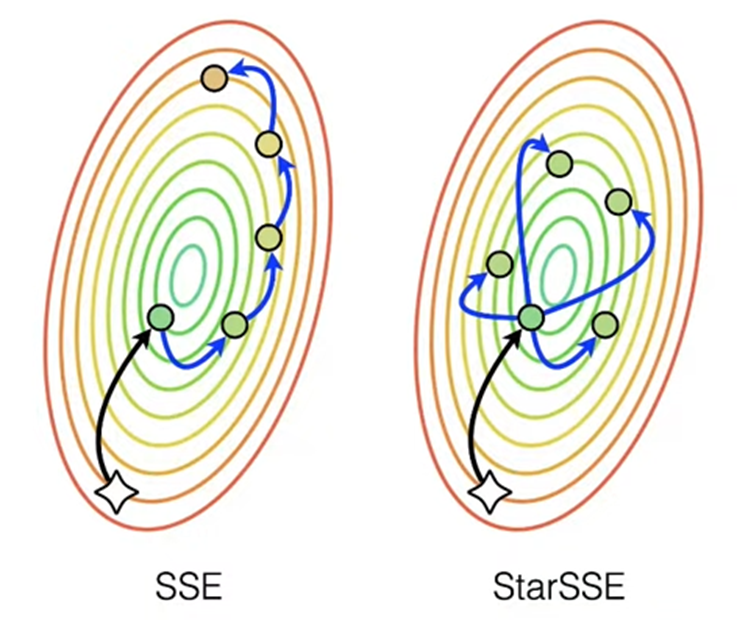
Авторы данного исследования попытались скомбинировать оба этих подхода, предложив новую архитектуру, которая даёт существенные преимущества по сравнению с предыдущими попытками. В частности, оказалось, что если перейти от последовательного файнтюна в ансамбле к параллельному, то производительность всей модели увеличится.
Помимо самой статьи с исследованием, можно почитать и её пересказ.
Обоснованное самообучение
Self-supervised learning или, если по-русски, самообучение — это сравнительно новый подход в ML, основанный на автоматическом формировании меток (псевдометок) на основе внутренней структуры данных либо некоторых базовых знаний, связанных с ними. Как можно догадаться, автоматизация разметки — во всяком случае, предварительная — экономит ресурсы при обработке больших датасетов, а потому представляет собой интересную альтернативу обучению с учителем.
Как и всякий молодой подход, он развивается в большинстве случаем эвристически, или, если угодно, методом научного тыка. Глядя на это, небольшая команда учёных под руководством CEO AIRI Ивана Оселедца решила подвести под самообучение хорошую математическую базу.
Исследователи стартовали с предположения, что многомерные данные лежат вдоль скрытого гладкого многообразия низкой размерности внутри многомерного пространства. Это позволило перейти на язык дифференциальных операторов (а именно оператора Лапласа — Бельтрами), после чего аппроксимировать их с помощью векторов и матриц. Оказалось, что в такой формулировке выучивание оптимальных представлений эквивалентно задаче о восполнении низкоранговой матрицы.
Теоретическое обоснование самообучения позволит, с одной стороны, придумывать его более оптимальные реализации, а с другой — расширить область его применения. Подробности можно найти в соответствующей статье, а также в блоге.
Спуск на тензорном поезде
Градиентный спуск как решение проблемы оптимизации был предложен ещё в XIX веке небезызвестным Коши, но до сих пор довольно популярен в ML и DS благодаря своей простоте. Его минусы также хорошо известны, и в первую очередь это застревание в локальных минимумах и «проклятие размерности» — когда число переменных оптимизируемой функции растёт, метод становится вычислительно неподъёмным. Ну и вишенка на торте — недифференцируемость функций, с которыми часто приходится иметь дело в Big Data.
Побороть все эти трудности призвана плеяда методов, которые можно объединить общим термином «безградиентная оптимизация». Зачастую они опираются на совершенно новые математические принципы.
Так, в одном из прошлых текстов на Хабре вы могли прочитать про то, как разложение в тензорный поезд — то есть представление многомерного массива в виде произведения нескольких тензоров малой размерности — помогает преодолеть «проклятие размерности». На этот раз те же авторы использовали такое разложение для решения задачи безградиентной оптимизации многомерной функции типа чёрного ящика. В экспериментах по сравнению с классическими и современными методами безградиентной оптимизации новый метод, прозванный авторами PROTES, продемонстрировал преимущества в подавляющем большинстве задач.

Как и во всех предыдущих случаях детали можно отыскать в статье и блоге.
И ещё кое-что
Если вас заинтересовали описанные выше исследования, предлагаю вашему вниманию запись одного из семинаров «ИИшницы» — серии митапов про искусственный интеллект, регулярно проводимых AIRI — который целиком был посвящён докладам, сделанным на NeurIPS 2023. Также ученые ответили на вопросы о своей работе в материале для N + 1.


