

Рис. 1. Термоакустический холодильник THEAC-25 с бегущей волной (слева) и термоакустический холодильник со стоячей волной Triton C-10c (справа)
Предыдущие части «1 статья»,«2 статья».
1) Термоакустический двигатель, холодильник и тепловой насос
1.1) Двигатель
В термоакустическом двигателе происходит преобразование тепловой энергии в акустическую. Такой процесс называется прямым термоакустическим эффектом.
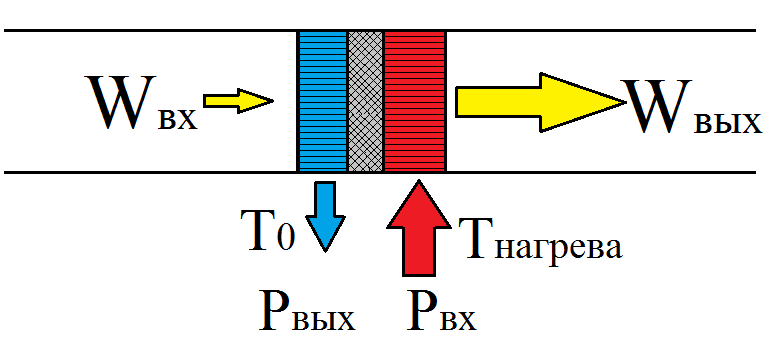
Рис. 2. Усиление мощности акустической волны в теплообменном аппарате двигателя
На вход теплообменного аппарата поступает волна маленькой мощности Wвх и усиливается, проходя через теплообменный аппарат двигателя до величины Wвых. Для того чтобы усилить волну, необходимо затратить тепловую энергию. Тепловая энергия Pвх подводиться при температуре нагрева Tнагр. Не вся тепловая энергия может быть преобразована в акустическую энергию, так как максимальная эффективность преобразования любой тепловой машины ограничена КПД цикла Карно. Поэтому приходиться сбрасывать часть тепловой мощности Pвых в окружающую среду. Температура, при которой осуществляется отвод тепла равна — Tо. Обратите внимание, что в двигателе направление роста температуры в теплообменном аппарате и направление в котором растёт акустическая мощность, совпадают.
1.2) Холодильник
В холодильнике реализуется обратный термоакустический эффект. То есть происходит всё наоборот, по сравнению с двигателем. На вход теплообменного аппарата холодильника поступает мощная акустическая волна Wвх, которая затухает в теплообменном аппарате до величины Wвых. Потеря мощности волны идёт на создание разности температур между теплообменниками.
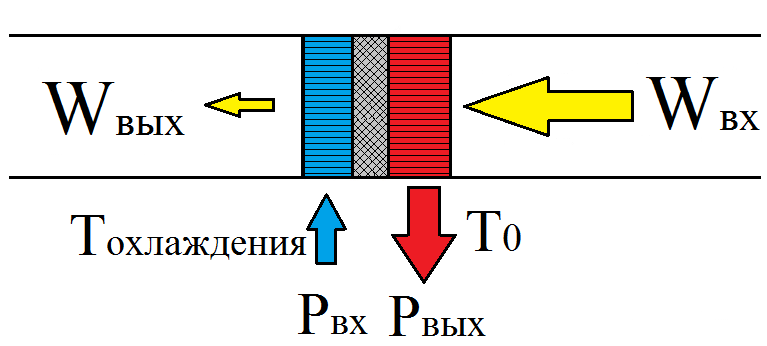
Рис. 3. Создание разности температур при затухании волны
Один из теплообменников начинает нагреваться, а другой начинает охлаждаться. То есть акустическая волна отбирает тепло у одного теплообменника и передаёт его другому. С нагревающегося теплообменника при этом необходимо сбрасывать в окружающую среду тепловую мощность Pвых, а на холодный теплообменник поступает тепловая мощность Pвх, которая и является полезной тепловой мощностью холодильника. Холодильник охлаждает какой либо объект до температуры Tохл.
1.3) Тепловой насос
Тепловой насос это, по сути, то же самое, что и холодильник, только с той лишь разницей, что в холодильнике полезной считается тепловая мощность, отбираемая у окружающей среды, а в тепловом насосе мощность, отдаваемая в окружающую среду (на различные нужды).
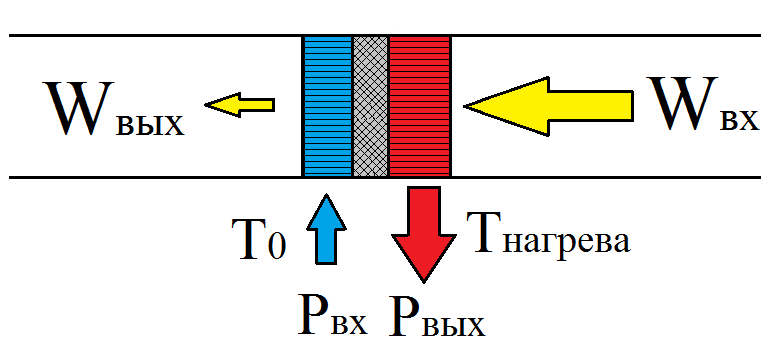
Рис. 4. Тоже создание разности температур при затухании волны, только полезной мощностью считается мощность нагрева, а не охлаждения
Обратите внимание, что как в холодильнике, так и в тепловом насосе направление в котором уменьшается температура в теплообменном аппарате противоположно направлению, в котором уменьшается мощность акустической волны, что свидетельствует о том, что реализуется обратный термоакустический эффект. Акустическую волну, поступающую на вход можно создавать при помощи двигателя, либо при помощи мощного динамика или поршня, подключённого к линейному электродвигателю.
2) Устройства со стоячей волной и устройства с бегущей волной
По типу волны в резонаторе термоакустические устройства делятся на два вида, на устройства с бегущей волной и на устройства со стоячей волной.
Посмотрим, в чём различия между бегущей и стоячей акустической волной.
2.1) Бегущая волна
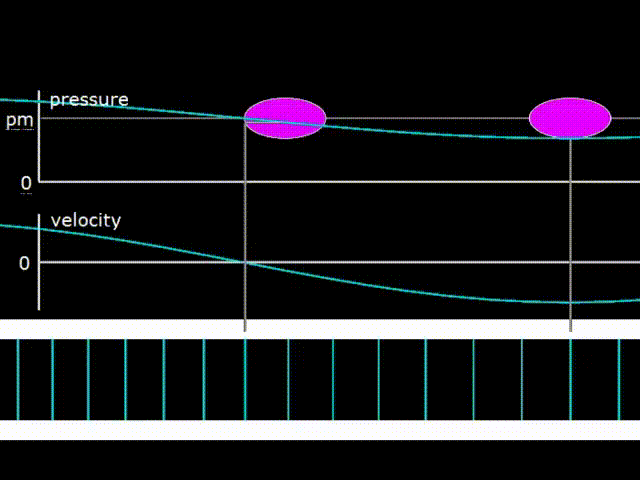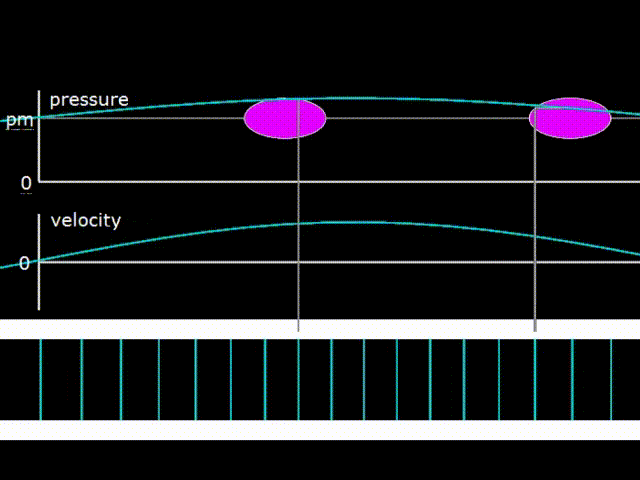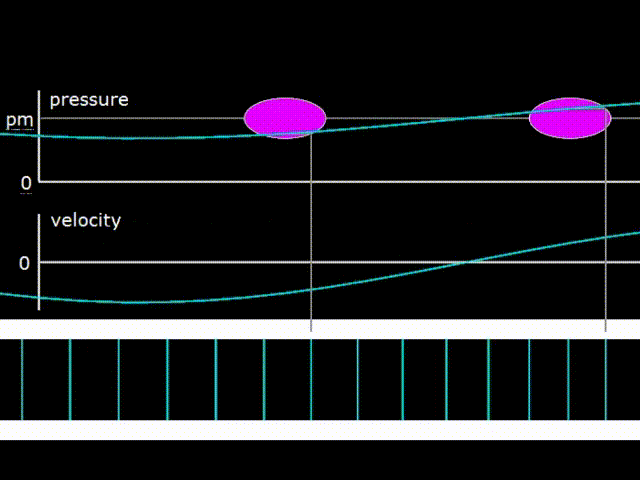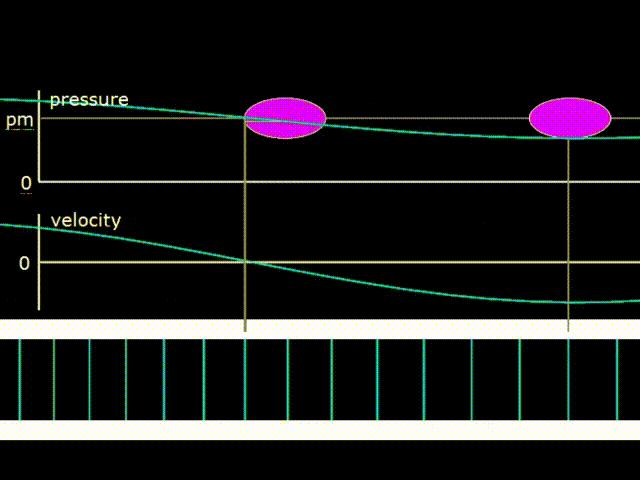
Гифка 1. График давления, скорости газа и изображение его смещения в бегущей волне
Бегущая волна бежит по резонатору на гифке 1 вправо. В бегущей волне колебания давления и скорости газа находятся в фазе. При этом происходит перенос энергии в направлении движения волны. Розовыми овалами на гифке 1 изображены диаграммы зависимости давления от координаты элементарных порций газа в различных точках внутри резонатора. Акустическая мощность, переносимая волной вправо численно равна площади розового овала, то есть площади PX диаграммы. Как видно, овалы в разных точках одинаковые, что говорит о том, что мощность волны при движении по резонатору не меняется. То есть, здесь не учитывается затухание волны при движении по резонатору.
Бегущая волна может распространяться в резонаторе, представляющем собой закольцованную трубу. При этом длина волны, соответствующая резонансной частоте такого резонатора будет равна длине самой трубы.
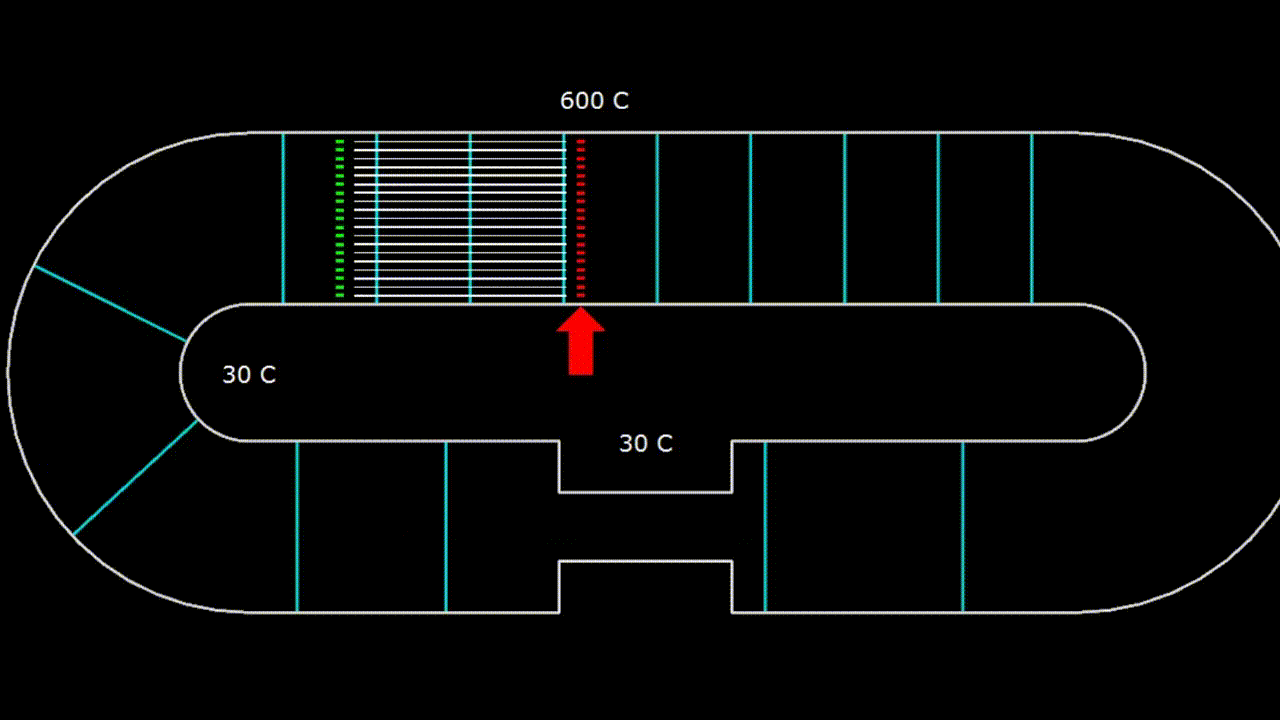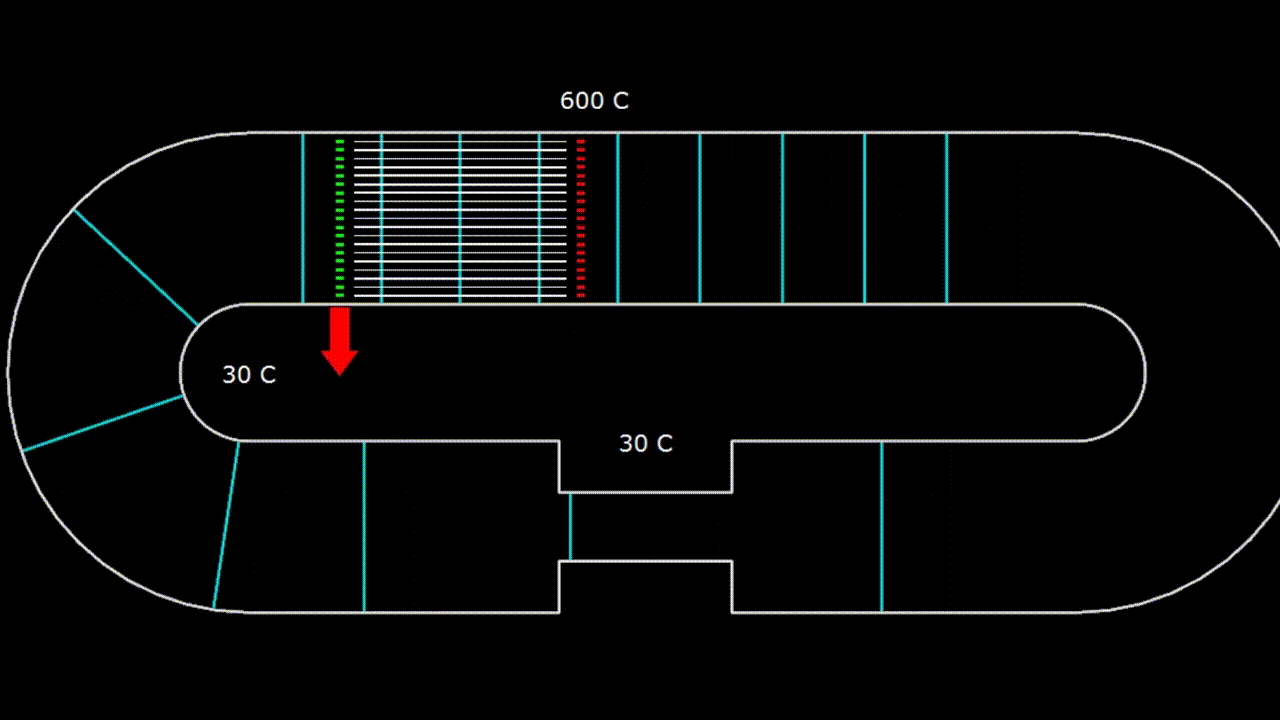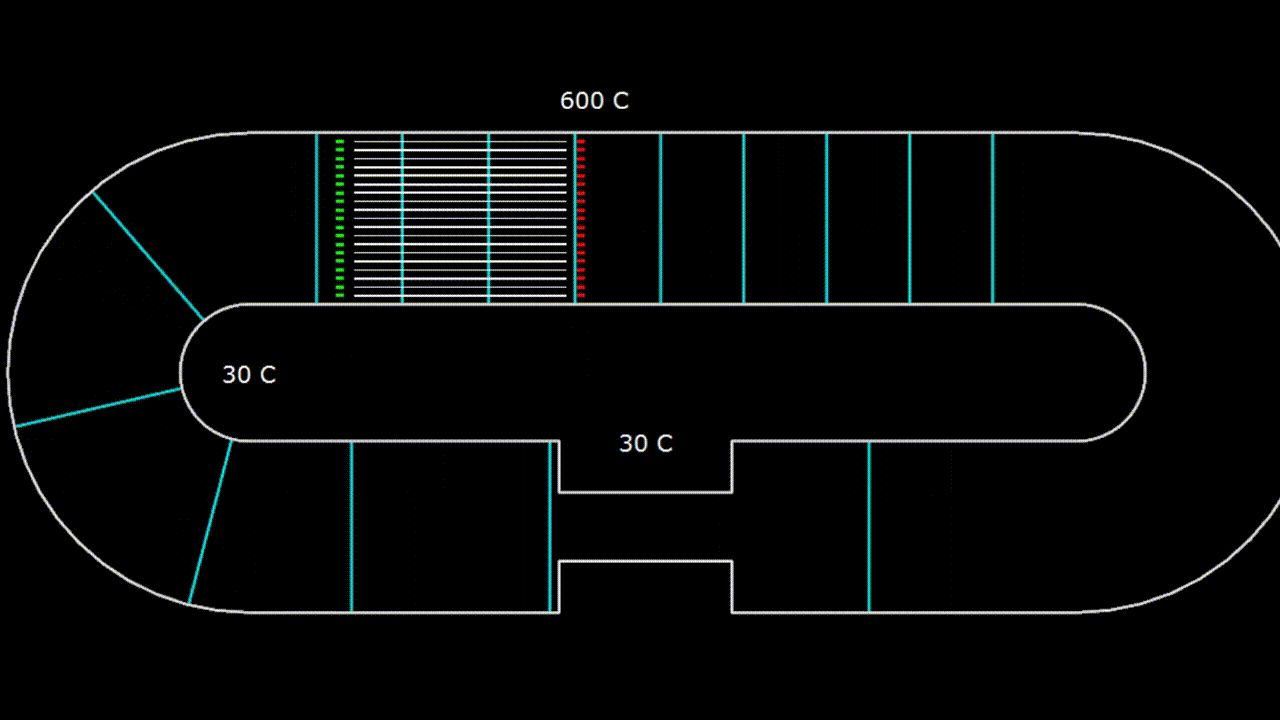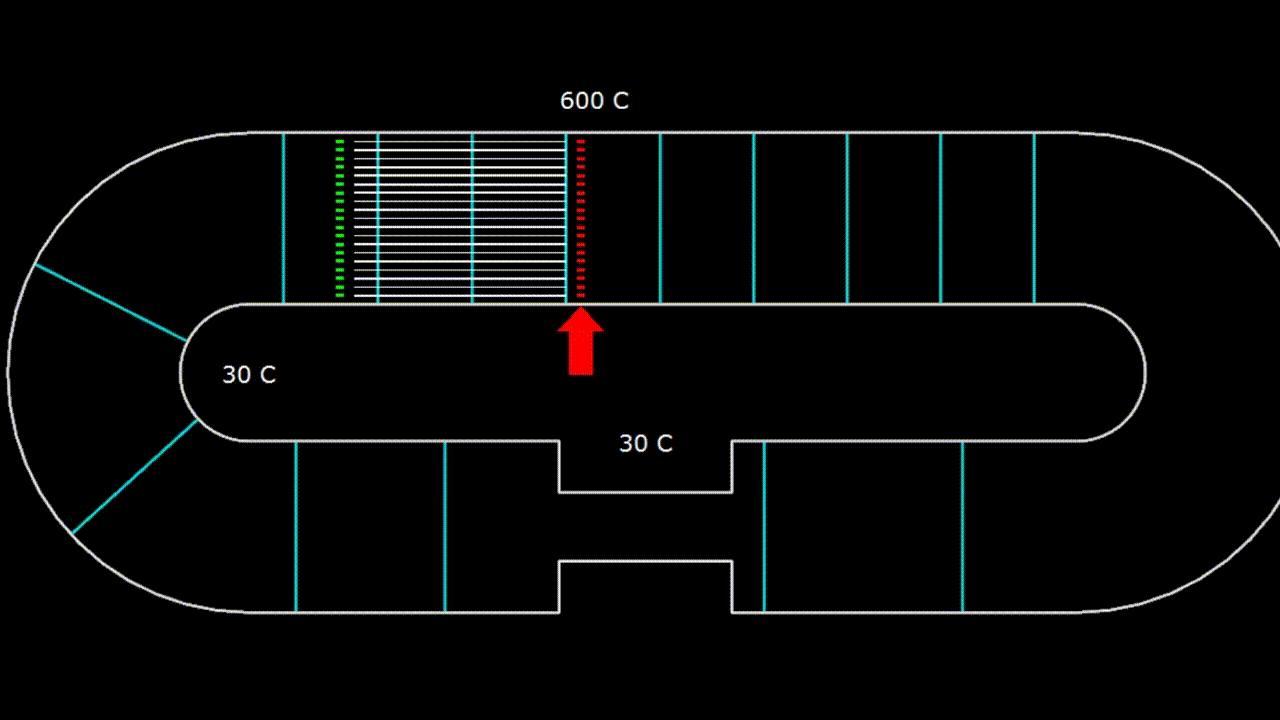
Гифка. 2. Устройство с бегущей волной
2.2) Стоячая волна
Стоячая волна – это сумма двух бегущих волн, распространяющихся в противоположных направлениях. Такая волна может возникнуть при отражении, от какого либо предмета и возвращении к источнику звука.
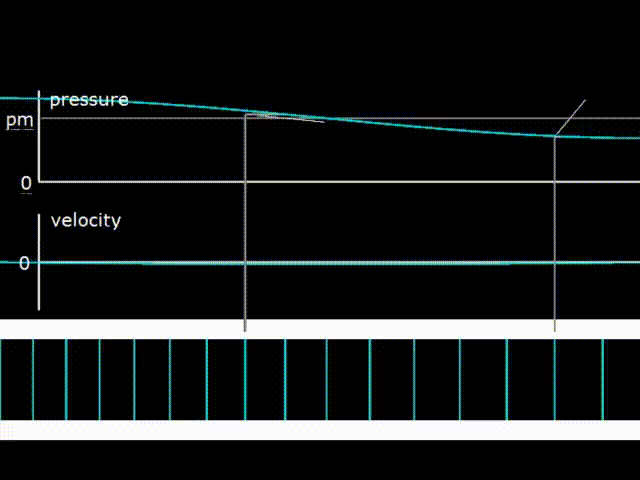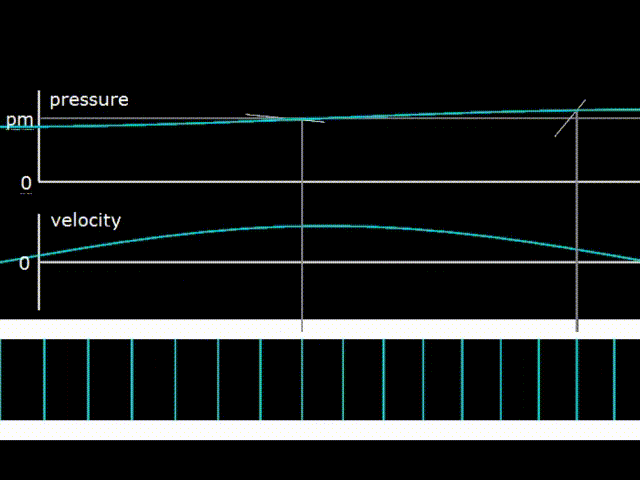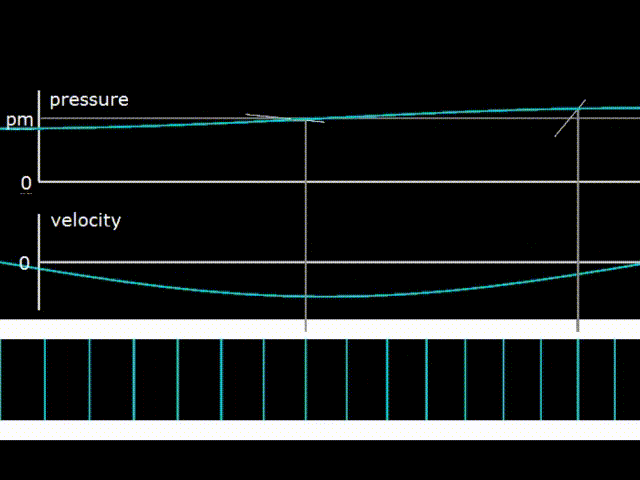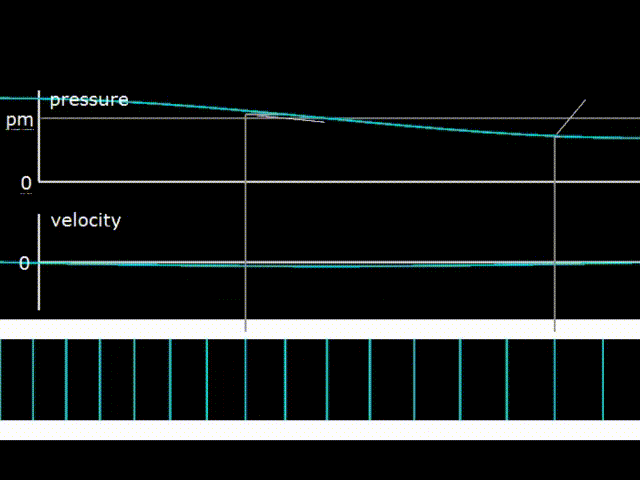
Гифка 3. График давления, скорости газа и изображение его смещения в стоячей волне
На гифке 3 изображена стоячая волна в полуволновом резонаторе, то есть в резонаторе с длиной, равной половине длины волны. Можно мысленно представить, что резонатор внизу на гифке 3 представляет собой трубу, заглушенную с двух сторон заглушками. При этом кто то, допустим, трясёт трубу, и газ внутри болтается между двух концов трубы. Так как концы трубы заглушены, то скорость газа на поверхности заглушек может быть только нулевая (что и видно на графике velocity). То есть на концах трубы возникают узлы скорости. Одновременно с этим видно, что на заглушках будут наблюдаться наибольшие по амплитуде колебания давления (антиузлы или пучности давления), а узел давления (точка, где нет колебаний) будет в середине трубы.
В стоячей волне разность фаз между колебаниями давления и колебаниями скорости составляют 90 градусов. При этом PX диаграммы во всех точках резонатора представляют собой линии, то есть фигуры, не имеющие площади. Соответственно переноса энергии в стоячей волне не происходит, ни в правую, ни в левую сторону. Но у самой волны естественно энергия при этом есть.
Стоячую волну в полуволновом резонаторе можно создать, поместив динамик или поршень на одном из его концов, производя колебания на резонансной частоте резонатора. А поместив дополнительно в резонатор теплообменный аппарат, можно создать термоакустический холодильник.
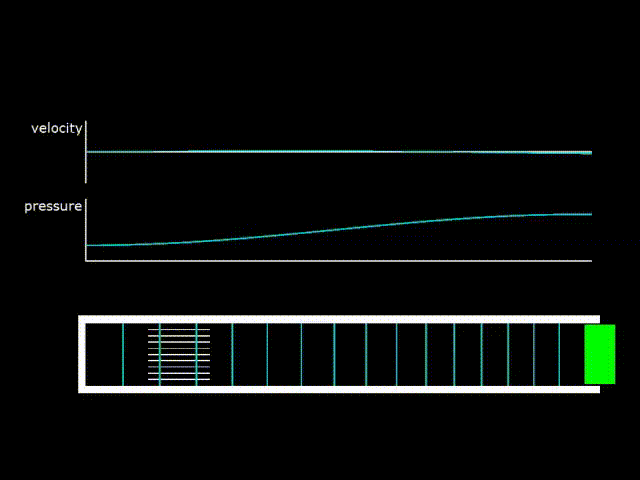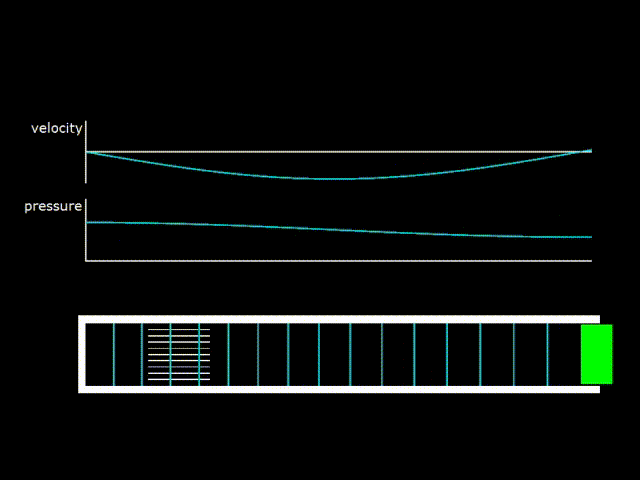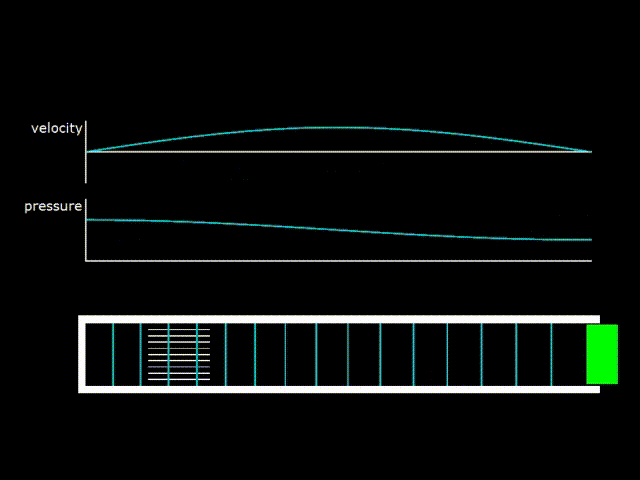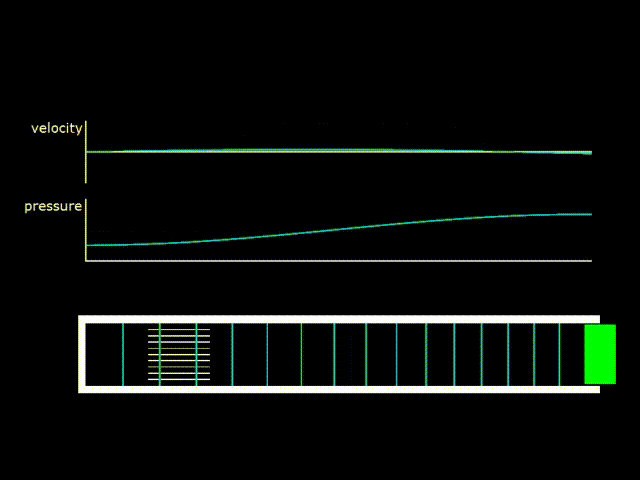
Гифка 4. Стоячая волна в полуволновом резонаторе. Слева в резонаторе расположен так называемый стек – аналог регенератора в двигателе с бегущей волной
Из-за рассеяния акустической энергии в резонаторе и в теплообменном аппарате получившаяся волна не будет чисто стоячей. Будет нужна постоянная подпитка энергией от поршня. На гифке 4 видно, что, так как поршень колеблется, то и газ у поршня колеблется вместе с ним. Возникает перенос акустической энергии от поршня в резонатор, который компенсирует потери энергии в резонаторе. Таким образом, хоть получившаяся волна очень близка к стоячей, но при более тонком рассмотрении представляет собой сумму стоячей и бегущей волны.
В реальных термоакустических устройствах тоже никогда не бывает чисто бегущей либо чисто стоячей волны. Волна всегда представляет собой нечто промежуточное, но при этом, если волна в устройстве очень похожа на стоячую, то устройство называют устройством со стоячей волной, а если волна похожа на бегущую, то называют устройством с бегущей волной.
3) Основные размеры
3.1) Длина корпуса
Длина корпуса — резонатора термоакустического устройства определяется длиной волны. Даже лучше сказать наоборот, что длина корпуса-резонатора определяет длину волны в резонаторе.
В устройствах со стоячей волной длина корпуса обычно равна половине длины волны. Например, для типичной для данного вида устройств частоты колебаний 300 Гц, длина корпуса при работе на воздухе составит около 0,56 метра, а при работе на гелии 1,65 метра.
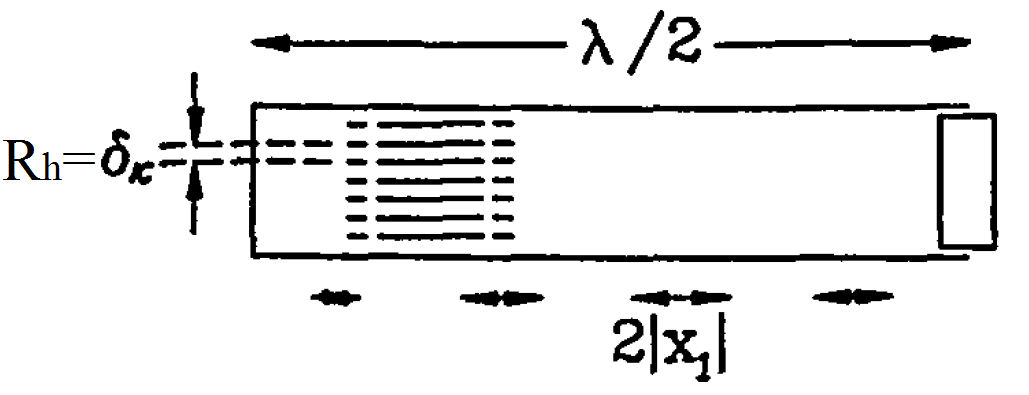
Рис. 5.Основные размеры устройства со стоячей волной
В устройствах с бегущей волной длина волны примерно равна длине корпуса. Типичная частота колебаний в таких устройствах – 100 Гц, при этом длина корпуса при работе на воздухе составит 3,4 метра, а при работе на гелии – 10 метров.
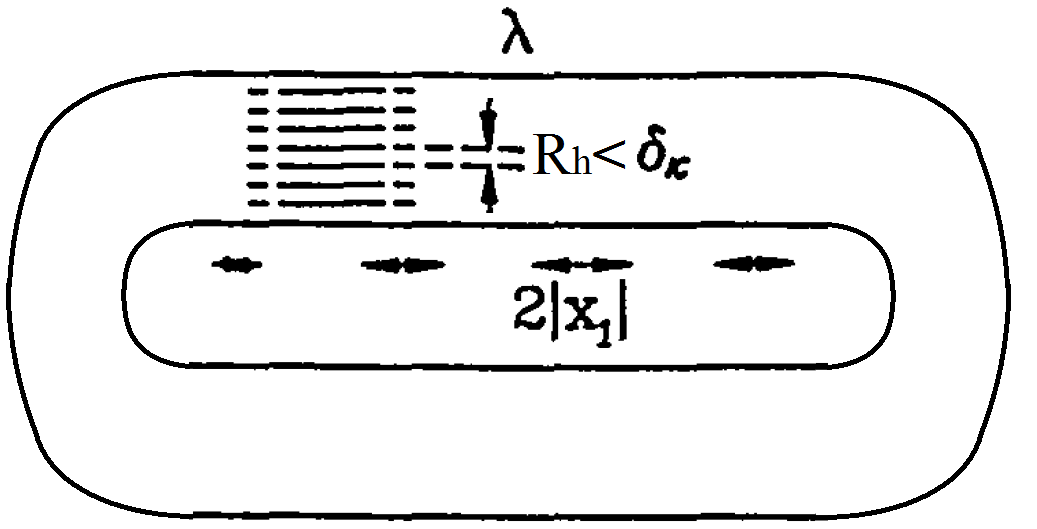
Рис. 6. Основные размеры устройства с бегущей волной
3.2) Диаметр корпуса
Диаметр корпуса определяется исходя из необходимой мощности устройства. Мощность растёт с увеличением диаметра устройства пропорционально площади поперечного сечения корпуса, так как пропорционально площади поперечного сечения растёт мощность теплообменного аппарата.
Резонатор представляет собой обычную трубу, желательно с гладкими стенками.
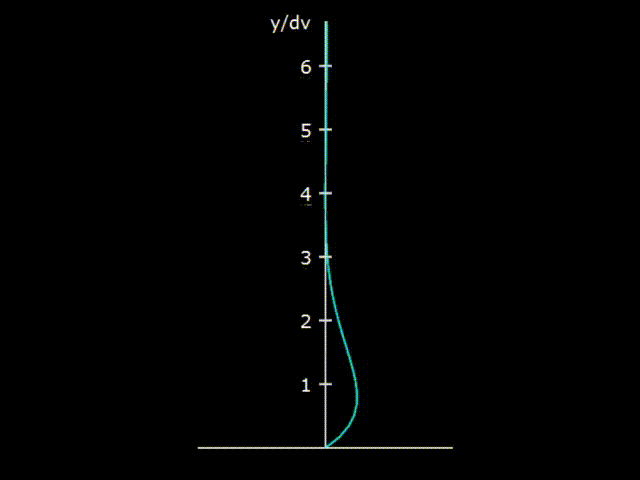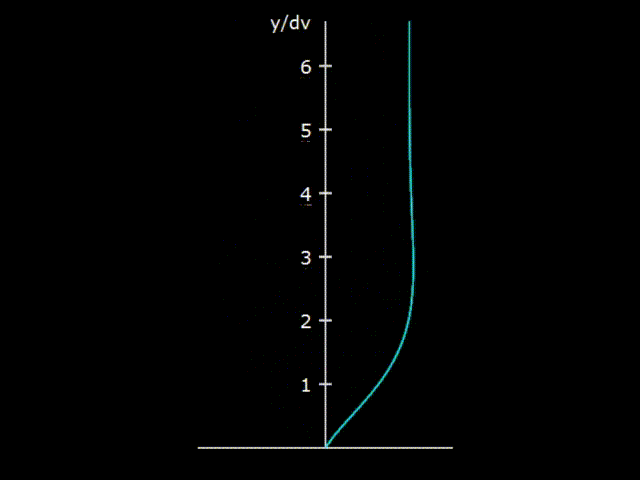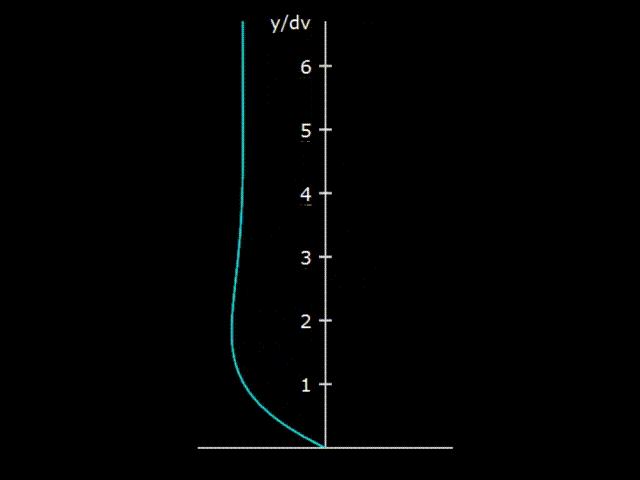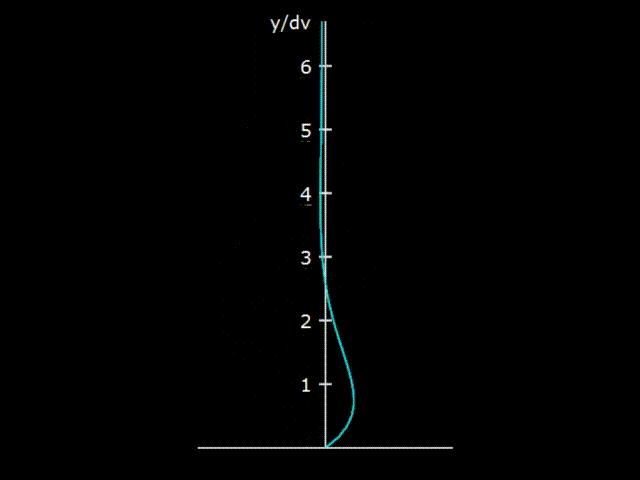
Гифка 5. Взаимодействие колеблющегося газа со стенкой резонатора
Если рассмотреть распространение акустической волны в резонаторе достаточно крупного диаметра (примерно от сантиметра и более), то выясняется, что газ в волне взаимодействует со стенкой резонатора далеко не во всём своём объёме, а только в небольшом приграничном слое, расположенном у стенки резонатора. На гифке 5 показано, что при колебаниях газа у стенки резонатора образуется необычная деформация скорости газа из-за трения о стенку. На поверхности стенки скорость газа нулевая, что обычно принято как граничное условие в большинстве гидродинамических задач.
Глубина вязкостного проникновения
Вертикальная ось на графике размечена в так называемых величинах вязкостного проникновения δν.
Глубина вязкостного проникновения является оценкой величины слоя, активно взаимодействующего со стенкой корпуса. Например, для акустической волны, распространяющейся в воздухе с нормальными условиями, с частотой 70 Гц, глубина вязкостного проникновения составляет 0,27 мм. На гифке 5 видно, что взаимодействие стенки и газа наблюдается при величинах и больших, чем глубина вязкостного проникновения, но, тем не менее, область достаточно активного взаимодействия волны со стенкой имеет величину только порядка 1 мм. В центре резонатора наблюдаются обычные акустические колебания, точно такие же, как если бы резонатора вообще бы не было. Соответственно рассеяние акустической энергии по причине трения о стенки происходит только в узком пограничном слое у стенки.
Глубина термического проникновения
В акустической волне происходят сжатия и расширения газа, при этом происходят колебания температуры газа из-за попеременного адиабатического нагрева и охлаждения. Так происходит в волне, распространяющейся в свободном пространстве. При движении волны в резонаторе, происходит взаимодействие волны со стенкой резонатора, и температура стенки начинает влиять на колебания температуры газа в акустической волне.
Точно так же как и для вязкостного взаимодействия со стенкой, для термического взаимодействия тоже есть величина, которая характеризует величину слоя газа, активно термически взаимодействующего со стенкой. Эта величина называется – глубина термического проникновения δκ. Колебания температуры газа у стенки деформируются точно так же как и скорость газа в предыдущем примере. Так что если просто сказать, что теперь на гифке 5 происходят колебания не скорости газа, а температуры и что теперь вертикальная ось размечена не в глубинах вязкостного проникновения, а в глубинах термического, то гифка 5 будет верна и для колебаний температуры. Численно глубина термического проникновения всегда больше, чем глубина вязкостного. Например для того же воздуха при нормальных условиях и при частоте колебаний 70 Гц глубина термического проникновения составит примерно 0,32 мм, что всего лишь в 1,185 раза больше чем глубина вязкостного в предыдущем примере.
Какие можно из всего этого сделать выводы?
Ну во первых, при достаточно крупном диаметре резонатора, волна почти никак ни вязкостно, ни термически не взаимодействует с резонатором. Резонатор только задаёт направление волны и тип волны. Отсюда следует, что для того чтобы передавать и отнимать у газа тепловую энергию, величина каналов (пор, отверстий, щелей) в теплообменном аппарате должна быть где то в районе величины термического проникновения, но ни в коем случае не намного больше этой величины.
Затем, так как глубины вязкостного и термического проникновения почти равны для любых газов и для любых частот, то термоакустические устройства обречены на то чтобы иметь потери связанные с трением газа о поверхность теплообменного аппарата.
3.3) Размеры каналов в теплообменном аппарате
У устройств с бегущей волной, для достижения максимальной эффективности, гидравлический радиус пор в теплообменном аппарате должен быть меньше, чем глубина термического проникновения Rh<δk, для того чтобы обеспечить хороший тепловой контакт между газом и поверхностью теплообменного аппарата. Это условие следует из уравнений термоакустики. Для регенератора это условие особенно важно. Обычно оптимальная величина гидравлического радиуса пор регенератора, где то от 3,5 до 6 раз меньше, чем глубина термического проникновения. Величина пор в теплообменниках влияет на устройство гораздо меньше, чем величина пор в регенераторе, по этому, обычно предпочитают увеличить размеры пор (каналов) в теплообменниках, относительно пор в регенераторе, для простоты изготовления.
Уравнения термоакустики с другой стороны говорят нам о том, что в устройствах со стоячей волной величина гидравлического радиуса пор стека (аналога регенератора в устройствах с бегущей волной), должна быть примерно равна глубине термического проникновения в газе. То есть, в устройстве со стоячей волной, величина пор в стеке должна быть, где то в 3,5-6 раз больше, чем в устройстве с бегущей волной при прочих равных. Величина пор в теплообменниках устройств со стоячей волной не так сильно влияет на эффективность устройства, как величина пор в стеке, так же как и в устройствах с бегущей волной.
3.4) Длина теплообменников и регенератора
В акустической волне каждая элементарная порция газа совершает гармонические колебания относительно своего положения равновесия с амплитудой X1 (см. рис. 5 и рис. 6). Значение оптимальной длины регенератора или стека обычно больше, чем величина смещения газа 2|X1|(больше, чем удвоенная амплитуда отклонения элементарной порции газа из положения равновесия). Если типичное значение для величины смещения — 1 см, то регенератор или стек может иметь длину от 1 см до 5 см, в зависимости от рабочей температуры. Величина длины теплообменников имеет тот же порядок, что и для регенератора.
4) Термодинамический цикл в устройствах со стоячей волной и в устройствах с бегущей
4.1) Двигатель и холодильник со стоячей волной
Термодинамический цикл, реализующийся в стеке устройства со стоячей волной наиболее близок к циклу Брайтона, который реализуется в газотурбинном двигателе.
Двигатель
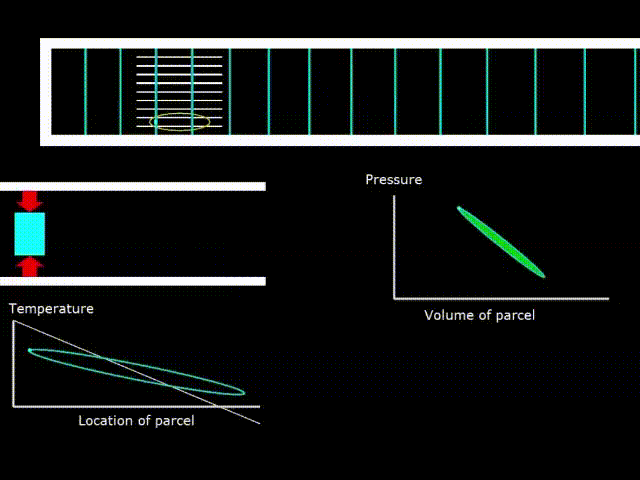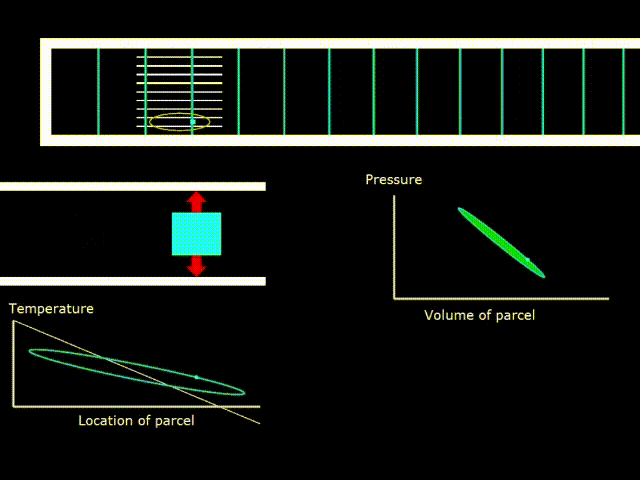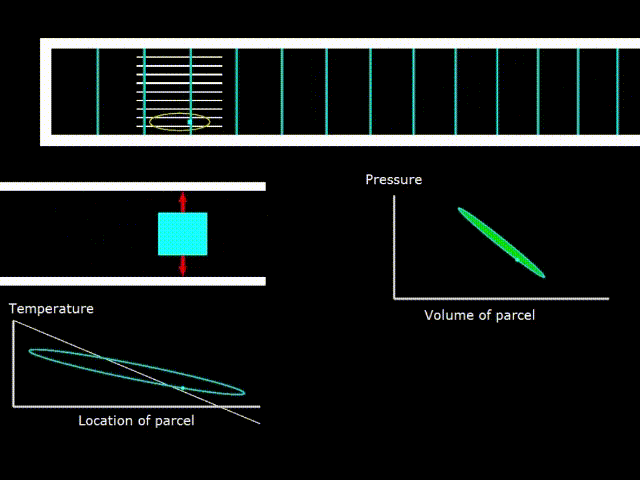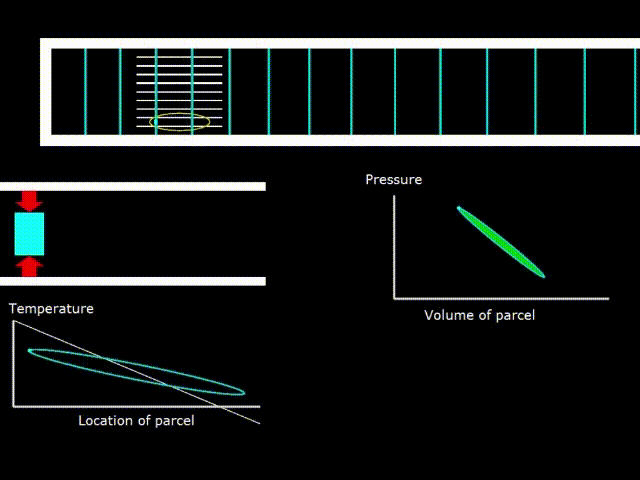
Гифка 6. Термодинамический цикл в двигателе со стоячей волной
На гифке 6. показаны колебания элементарного объёма газа между пластинами стека. Газ, совершая сжатия и расширения, изменяет свою температуру (график в левом нижнем углу). График зависимости температуры от координаты представляет собой фигуру похожую на овал (зелёная линия). Белой линией на графике отмечена температура поверхности стека. Можно видеть, что присутствует температурный градиент вдоль длины стека. То есть температура линейно снижается при движении от левого до правого конца стека.
Если белая линия температуры стека имеет наклон на графике больше, чем наклон овала — графика температуры газа, то устройство работает как двигатель.
В середине справа показана PV диаграмма – зависимость давления от объёма в элементарной порции газа. Площадь овала на диаграмме численно равна работе совершаемой над газом в случае двигателя и работе совершаемой газом в случае холодильника (теплового насоса).
Так как при работе со стоячей волной оптимальная величина размеров каналов стека примерно равна глубине термического проникновения, то термический контакт газа и твёрдой поверхности не идеален и температуры газа и стека, в какой либо конкретной точке стека могут отличаться друг от друга. Если бы тепловой контакт между газом и стеком был бы идеален, то тогда графики температуры газа и стека совпадали, так как газ бы мгновенно принимал температуру поверхности стека, в какой бы точке он ни оказался.
Критический градиент температуры в стеке
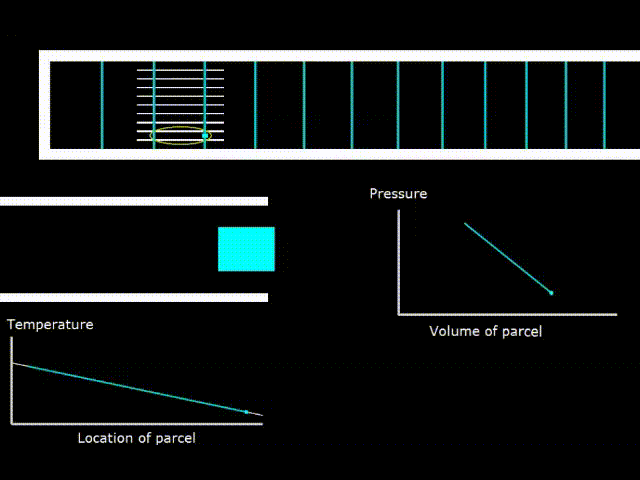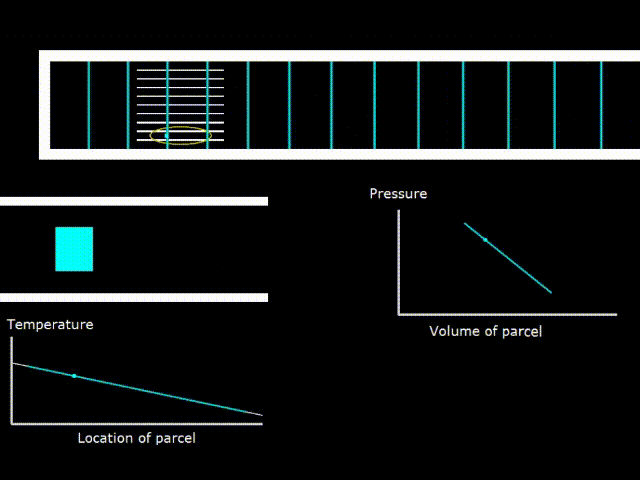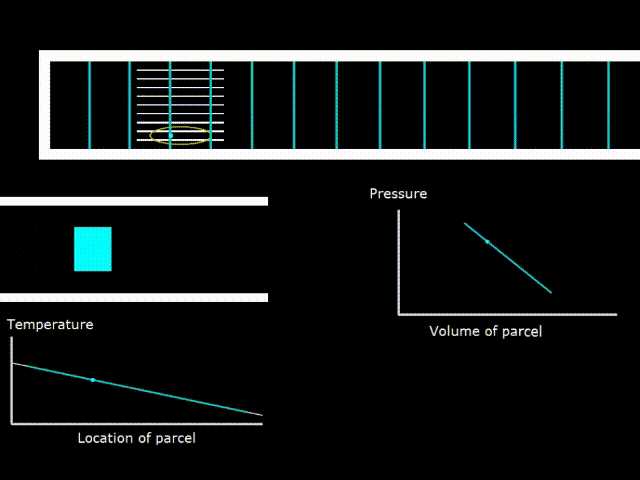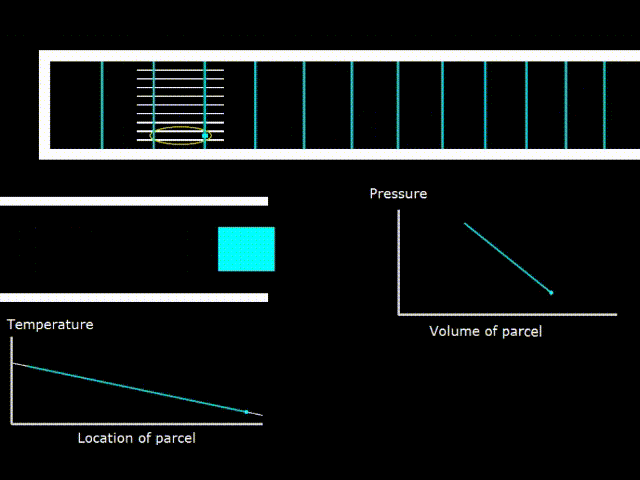
Гифка 7. Критический градиент температуры в стеке
Теперь возьмём двигатель и начнём уменьшать перепад температур на стеке, при этом, каким либо образом сохраняя амплитуду акустической волны, например с помощью динамика. При этом рано ли поздно, наступает состояние, при котором температура в элементарной порции газа в волне начинает колебаться так, что её температура начинает совпадать с температурой поверхности стека, где бы эта порция газа не находилась (гифка 7. зелёная и белая линии на графике температуры совпадают).
В таком случае, не совершается никакой работы в стеке (PV диаграмма представляет собой линию – фигуру, не имеющую площади)
Градиент температур в стеке, при котором реализуется описанный выше случай, называется критическим градиентом температур для данной конкретной волны. Устройство, с критическим градиентом температур абсолютно бесполезно для практического применения. Оно занимает положение ровно между двигателем и холодильником. Тем не менее, относительно него удобно сравнивать устройства, чтобы выяснить двигатель это или холодильник.
Холодильник
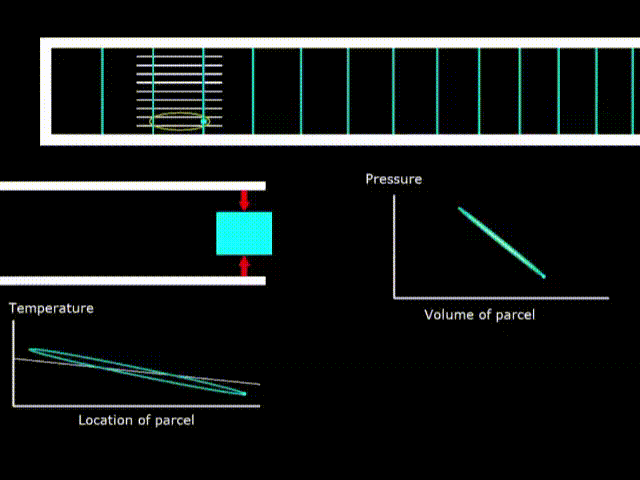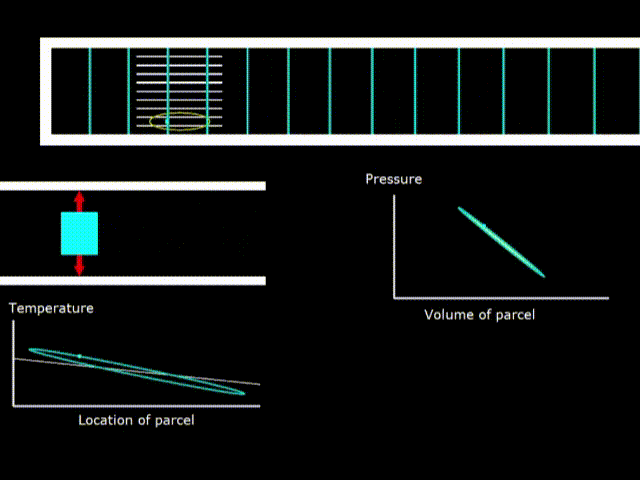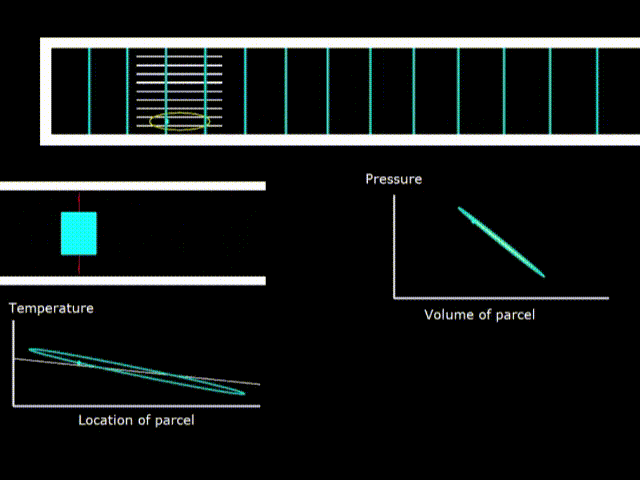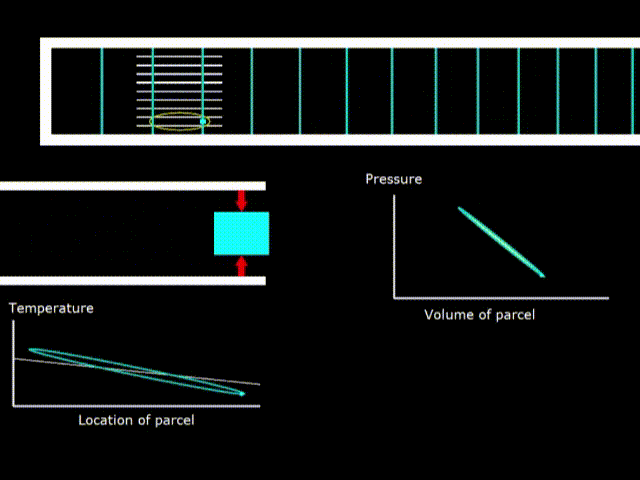
Гифка 8. Термодинамический цикл в холодильнике со стоячей волной
Если у температуры стека наклон меньше, чем у овала температуры газа, то устройство работает как холодильник.
Обратите внимание, что вращения зелёной точки на диаграммах двигателя и холодильника идут в противоположных направлениях, что говорит о том, что в одном случае производиться работа над газом, а в другом газ производит работу.
Что нужно сделать, чтобы превратить холодильник в двигатель? Нужно либо увеличить температурный градиент в стеке, при сохранении амплитуды акустической волны, либо уменьшить амплитуду волны при сохранении температурного градиента.
4.2) Двигатель и холодильник с бегущей волной
Термодинамический цикл, реализующийся в регенераторе устройства с бегущей волной наиболее близок к циклу Стирлинга, который реализуется в одноимённом двигателе.
В устройствах с бегущей волной реализуется случай идеального термического контакта между газом и поверхностью регенератора, благодаря маленькому оптимальному размеру пор.
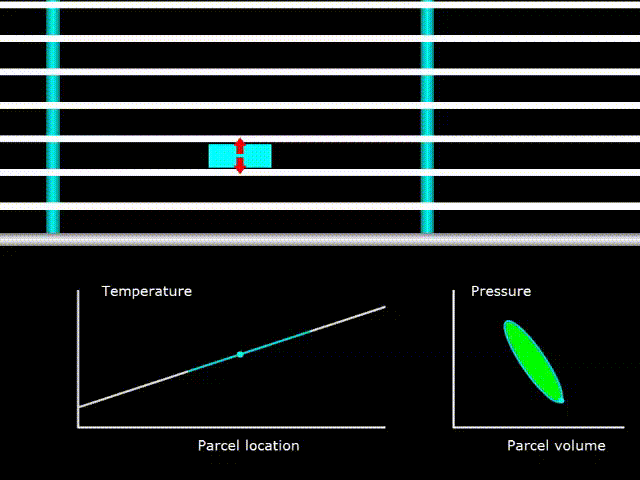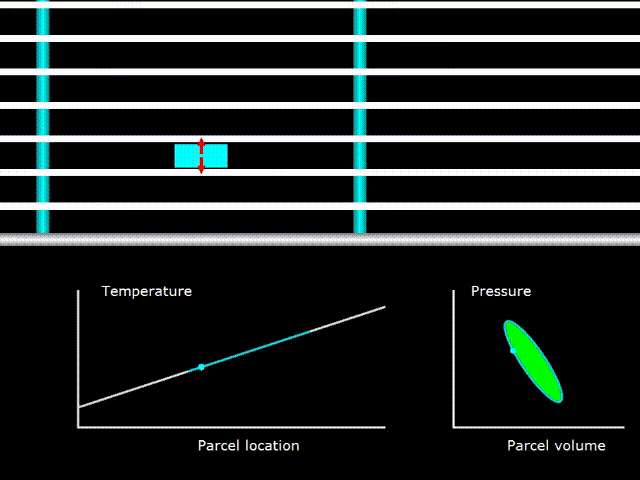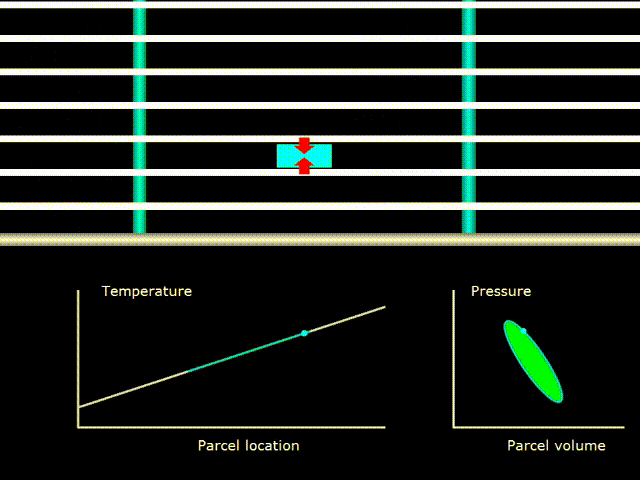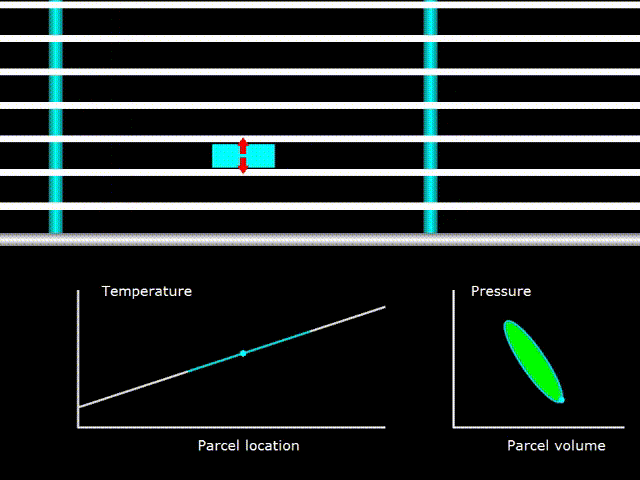
Гифка 9. Термодинамический цикл в двигателе с бегущей волной
Здесь температура газа (зелёная линия на графике температуры) совпадает с температурой регенератора во всех его точках (белая линия на графике температуры). PV диаграмма в правом нижнем углу говорит о том, что производиться работа над газом.
При этом нужно понимать, что хоть графики температур газа и регенератора совпадают, но это не устройство с критическим градиентом температуры в понимании описанном ранее. В устройствах со стоячей волной нужно было подобрать необходимый температурный градиент для данной волны, чтобы он совпал с колебаниями температуры в акустической волне. В устройствах же с бегущей волной из-за того что поры в регенераторе очень маленькие, всегда обеспечивается хороший термический контакт между регенератором и газом. Поэтому критический градиент температуры в устройствах с бегущей волной существует всегда и этот термин здесь теряет какой либо смысл. Как же тогда производиться работа над газом? Ведь при критическом градиенте температур, в случае устройства со стоячей волной, никакой работы не было. Всё дело в том, что при критическом градиенте температур не производиться работы над газом именно в стоячей волне, а в бегущей волне другая разность фаз между колебаниями давления и скорости газа и работа в данном случае наоборот, максимальна.
Для холодильника с бегущей волной графики будут выглядеть точно так же как и на гифке 9, за исключением того, что зелёная точка на PV диаграмме будет вращаться в другую сторону, что будет свидетельствовать о том, что газ совершает работу, а не над газом совершается работа.
В заключение, всем кто хочет по подробнее узнать о термоакустике, хочу порекомендовать книгу Г. Свифта, который внёс огромный вклад в термоакустику, работая в Лос-Аламосской национальной лаборатории:
Swift G.W. Thermoacoustic engines and refrigerators: a short course. Los Alamos: Los Alamos National Laboratory, 1999. 179 p. URL: ссылка для скачивания
Так же, прикрепляю анимации термоакустических процессов, созданные командой Г. Свифта:
ссылка для скачивания. Для просмотра анимаций нужно распаковать архив, поместить его в папку program files на жёстком диске (иначе почему то они не работают). Все анимации для windows находятся в папке EXEs.
В этой статье я пересказал только небольшую часть того что есть в этой книге, при этом не используя математику. В оригинале всё гораздо интереснее.
Источник


