
Наблюдая за работой иллюзиониста или фокусника, в голове всегда возникает вопрос «как он это делает?». Порой кажется, что трюк настолько нереален, что начинаешь верить в волшебство и магию. Однако, как бы прагматично это не звучало, магия заключается не в каких-то таинственных силах и заклинаниях, а в талантливом и весьма креативном применении точных наук. Многие фокусы, которые поражают воображение зрителей, являются не более чем устройствами, объединяющими в себе инженерию и физику. Одним из самых популярных физических инструментов фокусника всегда была оптика, а точнее зеркала и стекла. Еще тысячи лет тому назад в Древнем Китае и Японии ремесленники научились делать бронзовые зеркала, которые выглядели как обычное зеркало, если человек смотрел на свое отражение. Но если на него падали прямые солнечные лучи, то волшебное зеркало показывало какое-то изображение. Лишь в начале XX века ученые сообразили, что работа этого устройства основана на том, что изображение, отбрасываемое на обратную сторону зеркала, создает небольшие вариации поверхности, которые вызывают формирование нового изображения. И вот уже в XXI ученые из OSA (Оптическое общество) решили осовременить древнекитайское волшебное зеркало, использовав жидкие кристаллы. Как было создано волшебное зеркало 2.0, каков принцип его работы, и где оно может найти свое практическое применение? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.
Основа исследования
Возвращаясь к истокам, а именно к зеркалам из Древнего Китая, стоит отметить, что первые такие устройства датируются 2000 годом до н.э. Это были литые бронзовые зеркала, которые работали как обыкновенное зеркало при просмотре собственного отражения. Однако, когда солнечный свет падал прямо на зеркало, оно действовало как слегка параболическое, формируя изображение (соответствующее тому, что изображено на задней стенке зеркала) на полу или стене.
Подобный эффект можно наблюдать при отражении солнечных лучей от больших окон вниз на улицу. Хотя окно кажется плоским и не сильно искажает изображение, когда мы смотрим через него, небольшие деформации от натяжения по краям приводят к неравномерному отражению на земле в форме буквы «X».
Подобное явление, хоть и применялось в качестве забавного трюка тысячи лет тому назад, стало основой для вполне серьезного метода измерения поверхностных деформаций кремниевых пластин, названного методом Макио (от японского слова, обозначающего «волшебное зеркало»). Преимущество этого подхода в том, что он очень прост и практичен для промышленного применения по сравнению с другими методами, такими как интерферометрия или атомно-силовая микроскопия.
Эффект волшебного зеркала можно количественно объяснить с помощью стандартной теории дифракции. Однако окончательное понимание того, как изображения формируются из волшебных зеркал, было получено лишь в 2005 году сэром Майклом Берри (“Oriental magic mirrors and theLaplacian image”). В своем труде он установил, что интенсивность изображения задается в первом приближении лапласианом* высоты поверхностных рельефов на зеркале.
Оператор Лапласа (лапласиан, оператор дельта)* — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом Δ.
Принцип волшебного зеркала может быть применен к устройствам, работающим на просвет, так называемым «магическим окнам», которые могут производить аналогичный эффект, формируя лапласовское изображение за счет очень незначительных деформаций толщины. В частности, поверхность должна быть достаточно «гладкой» с плавными вариациями, чтобы каустика* не образовывалась до появления изображения.
Каустики* — в оптике это особые линии (в двумерном случае) и особые поверхности, вблизи которых резко возрастает интенсивность светового поля.
Было показано, что интенсивность лапласовского изображения выражается через высоту рельефа поверхности h по формуле: ILaplacian Mirror(r, Z) ≃ 1 + Z∇2h(r). В данном случае Z = 2D/M и r = R/M — масштабированное расстояние по направлению распространения и поперечному положению от центра зеркала соответственно. D и R — расстояние от зеркала и поперечное положение изображения соответственно.
Однако лапласовское изображение, создаваемое волшебным окном, зависит от относительного показателя преломления окна (n) в дополнение к высоте рельефа поверхности (h), которая определяется выражением:

где z – расстояние плоскости изображения от плоскости окна; R — поперечное расстояние от центра окна.
Следовательно, при любом данном изображении можно найти необходимую поверхность волшебного окна или зеркала путем решения уравнения Пуассона в поперечной плоскости.
Ученые отмечают, что в последнее время появился большой интерес к проблеме формирования интенсивности света, часто называемой оптикой произвольной формы. В рассматриваемом нами сегодня труде ученые решили показать, как волшебные зеркала/окна могут быть реализованы с помощью плоских оптических устройств.
В результате использовались устройства на основе жидких кристаллов (LC от liquid crystal), отражающий пространственный модулятор света (SLM от spatial light modulator) и оптический фазовый элемент Панчаратнама-Берри (PBOE от Pancharatnam–Berry optical phase element) для создания волшебного зеркала и волшебного окна соответственно. Также использовалась теория Лапласа, дающая более прямой и простой подход к расчету желаемых фазовых моделей в отличие от других методов (например, каустического моделирования).
Изображение №1
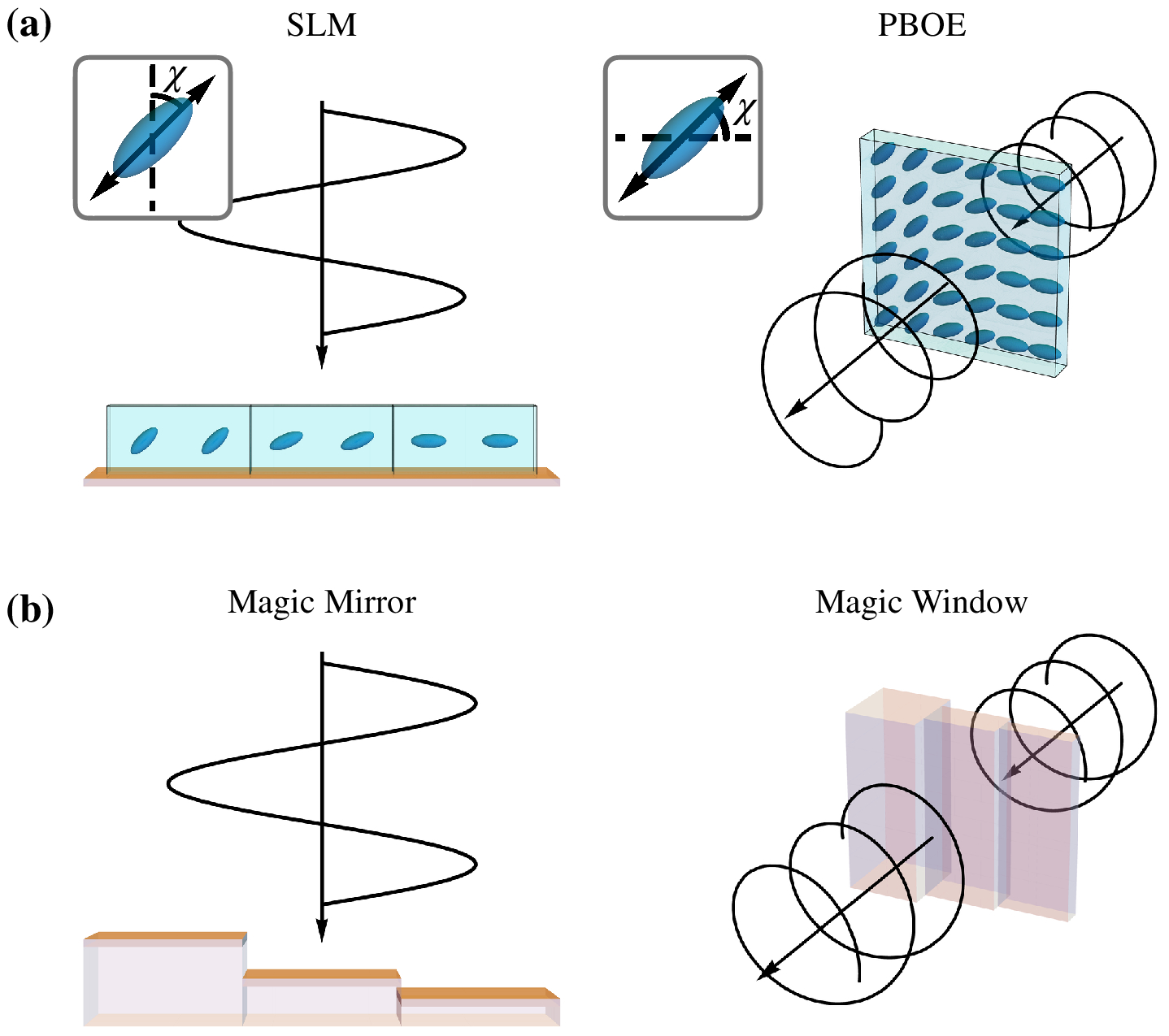
На 1a показано, как можно запрограммировать или изготовить эти два типа LC-устройств, чтобы они действовали как отражающие или пропускающие поверхности, показанные на 1b.
Оба типа устройств основаны на одноосном двойном лучепреломлении составляющих его нематических LC для реализации эффекта волшебного зеркала/окна. С одной стороны, стандартные LC на кремниевых SLM опираются на отражающую объединительную панель, которая вращает LC вокруг оси, перпендикулярной направлению распространения падающего оптического луча.
Таким образом, результирующая оптическая среда определяется двумя собственными состояниями линейной поляризации. Первый проходит вдоль оси вращения и определяется показателем преломления n0 — обычным показателем преломления LC. Второй ортогонален направлению распространения луча и оси вращения и имеет показатель преломления n(χ) = ((cos2χ)/n02 + (sin2χ)/ne2)-1/2, где ne — коэффициент необыкновенности*, а χ — угол поворота LC.
Двойное лучепреломление* — оптическое свойство анизотропных материалов, в которых показатель преломления зависит от направления распространения света.
Утрировано говоря, один луч (называемый необыкновенным лучом) изгибается или преломляется под углом при прохождении через среду; другой луч (называемый обычным лучом) проходит через среду без изменений.
Следовательно, подвергая SLM оптическому лучу, поляризованному вдоль этого второго направления, можно наложить луч, управляемый относительным углом LC, на поперечный фазовый профиль. Таким образом, SLM может работать как волшебное зеркало, если его запрограммированный поперечный фазовый профиль повторяет профиль высоты зеркала.
В другой ситуации, LC в PBOE вращаются вокруг оси, параллельной направлению распространения оптического луча. Результирующие собственные состояния поляризации, таким образом, либо выровнены, либо ортогональны оси ориентации LC и имеют индексы ne и n0 соответственно.
Когда толщина этой системы придает фазовый сдвиг π между этими двумя линейными поляризациями, тогда падающий луч с круговой поляризацией испытывает фазовый сдвиг ±2χ, сопровождаемый переворотом хиральности при распространении такой LC-ячейки, где χ — угол поворота LC.
PBOE используют это явление, поворачивая угол ориентации LC поперек пропускающего оптического дисплея, чтобы придать желаемый фазовый профиль лучу с круговой поляризацией. Таким образом, LCPBOE действует как волшебное окно, если он имеет схему ориентации LC, которая создает тот же фазовый профиль, что и вызванный изменениями толщины окна.
PBOE благодаря эффекту, известному как спин-орбитальная связь углового момента света, также позволяют реализовать фазовое распределение, зависящее от поляризации. Таким образом, можно наблюдать изображение, полученное от фазы или ее негатива, переключая входную поляризацию с левой на правую.
Результаты исследования
Волшебное зеркало из жидких кристаллов
Изображение №2
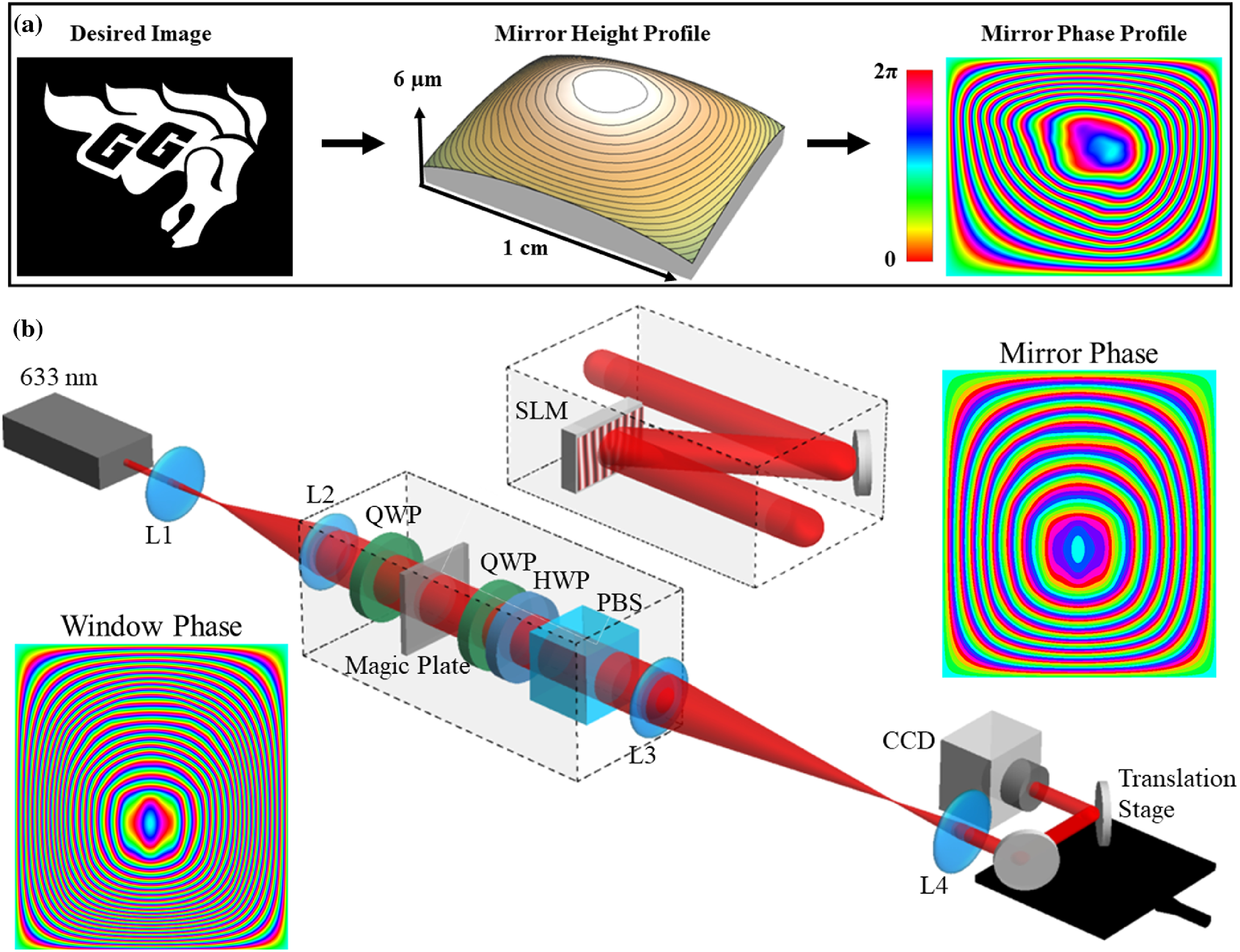
Волшебное зеркало было реализовано с помощью SLM с разрешением экрана 800 на 600 пикселей. На 2b показаны детали экспериментальной установки как для волшебного зеркала, так и для волшебной пластины (окна).
Учитывая желаемое изображение, вычисляется требуемая фазовая картина зеркала. Существует свобода увеличения крутизны диаграммы направленности, т. е. увеличения количества раз, когда фазовая характеристика изменяется от 0 до 2π. Это можно рассматривать как изменение вогнутости зеркала, что приводит к изменению скорости формирования изображения. В практических условиях необходимо соблюдать осторожность при выборе размера окна и крутизны фазы. Из-за расходимости луча изображение, которое формируется слишком медленно, теряет свою резкость. При этом рисунок должен быть достаточно гладким, чтобы не образовывались каустики перед плоскостью изображения.
Проявление логотипа «Gee-Gees», создаваемого волшебным зеркалом на жидких кристаллах, показанное на расстоянии 5 см.
Фазовая картина загружалась в SLM с добавлением вертикальной решетки. SLM освещался лазерным лучом с увеличенной формой гауссова луча, чтобы имитировать входную когерентную плоскую волну. Был выбран первый порядок дифракции, а остальные были отфильтрованы с помощью диафрагмы в центре 4f системы линз, чтобы удалить непреобразованный свет, возникающий из-за неэффективности SLM. В дополнение к выбору первого порядка дифракции 4f система линз также использовалась для изображения плоскости SLM и измерения интенсивности на разных расстояниях распространения. Эволюция распределения интенсивности регистрировалась на CMOS-камере от плоскости SLM до плоскостей формирования изображения.
Проявление логотипа «Structured Quantum Optics», создаваемого волшебным зеркалом на жидких кристаллах, показанное на расстоянии 5 см.
Как отмечают сами ученые, основной целью эксперимента было показать волшебное зеркало и волшебную пластину, закодированные с использованием теории Лапласа, с использованием технологии LC в SLM и PBOE.
Для этого необходимо было сгенерировать фазовую картину, соответствующую выбранному изображению интенсивности. Эта фазовая картина затем отображалась на SLM и PBOE. Шаблоны изображений, которые использовались в опытах, были преобразованы в растровую форму, так что пиксели содержали только 1 или 0 по отношению к значению интенсивности (2a).

Изображение №3
На основании уравнения выше дискретизированная функция интенсивности I(R, z) использовалась для определения высоты рельефа поверхности h(r), где r = r(R) в плоскости изображения.
Волшебная пластина из жидких кристаллов
Далее ученые объединили концепцию формирования изображения посредством волшебного окна и связи между фотонной поляризации и волновым фронтом. В основе созданного устройства, названного спин-орбитальная волшебная пластина, лежат PBOE, т.е. пластины из одноосных анизотропных материалов (в данном случае жидких кристаллов) с необыкновенной ориентацией осей, меняющейся в пространстве в плоскости пластины. Действие элемента PBOE с необыкновенной ориентацией оси χ(r)/2 и (пространственно однородным) замедлением (δ) определяется формулой:

где e+ и e— обозначают орты* левой и правой круговой поляризации соответственно.
Орт (единичный вектор)* — вектор нормированного пространства, длина которого равна единице.
Два единичных вектора на плоскости.
Оптическое запаздывание образца можно регулировать, подавая переменное напряжение на пластину. Идеально настроенный PBOE с δ = π приводит к полному преобразованию входной круговой поляризации в противоположную направленность с добавлением желаемой фазы ±χ(r), где χ(r) — обратный лапласиан изображения. Таким образом, меняя состояние падающей поляризации с левого на правое, можно получить на выходе фазу +χ(r) или —χ(r) соответственно.
Из-за разных знаков фазы две компоненты круговой поляризации распространяются по-разному, как это описывается интегралом дифракции Френеля:
E±(r, z) = ∫ K(r, rʹ, z)E±(rʹ, 0)d2rʹ
где K(r, rʹ, z) = exp[ik|r – rʹ|2/2z]eikz/iλz.
Из K(r, rʹ, z) = K*(r, rʹ, —z) следует, что E+(r, z) =E—*(r, z).
Как следствие, если одна круговая поляризация испытывает формирование изображения, которое сфокусировано из-за радиального изменения χ(r), противоположная круговая поляризация будет расфокусирована, и изображение из уравнения №1 будет отрицательным (т. е. негативом).
В качестве тестового изображения ученые решили использовать логотип университета Оттавы. На изображении №2 показана экспериментальная установка и фазовая картина, записанная на пластине волшебного окна. Пластина была изготовлена из пары ITO-стекл (оксид индия-олова), покрытых полиамидом методом центрифугирования. Затем стекла удерживались на расстоянии в 4 мкм друг от друга и склеивались с помощью эпоксидного клея.
Проявление логотипа Оттавского университета, создаваемого волшебным зеркалом на жидких кристаллах, показанное на расстоянии 5 см.
Использованный в устройстве полиамид можно фотовыравнивать посредством освещения линейно поляризованным УФ-светом. Ориентация полиамида может быть изменена посредством изменения поляризации падающего УФ-луча попиксельно с помощью цифрового микрозеркального устройства (DMD от digital micromirror device).
Рисунок, написанный на полиамиде, определяет ориентацию молекул LC, которые добавляются между пластинами на последующей стадии. Данный рисунок (шаблон) был создан с 32 фазовыми шагами, таким образом, 32 настройки поляризации освещают разные части пластины.

Изображение №4
При линейно поляризованном входе наблюдалось одновременное формирование логотипа Оттавского университета и его негатива (с несовершенным перекрытием из-за линзирования, зависящего от поляризации) (4а). Появление негатива связано с входной составляющей правой круговой поляризации, которая приобретает фазу —χ(r). Вполне возможно выделить либо негатив, либо само изображение логотипа, выбрав входную правую или левую поляризацию соответственно.
На 4b показано теоретическое моделирование эволюции интенсивности от источника с низкой поперечной когерентностью. Источник моделировался путем дискретизации поперечной плоскости в областях, где все пиксели находятся в фазе, и наложения случайного фазового шума между различными областями. Таким образом, поперечная длина когерентности была пропорциональна ширине области, которая была фиксированной в данном опыте (15 пикселей). Моделирование показывает результаты, усредняющие более 200 реализаций случайного шума (равномерно распределенного между 0 и 2π).
Поляризационная направленность изображения, создаваемого волшебным окном при проявлении (левая круговая поляризация — красный, а правая — зеленый).
Аналогичные эффекты наблюдались и при освещении когерентным лазерным лучом. Был использован гелий-неоновый лазер (λ = 633 нм), изготовленный с левой/правой круговой или линейной поляризацией. Результирующая интенсивность при входной левой круговой поляризации соответствовала искомой картине (4c и 4d). Также можно заметить наличие полос из-за поперечной когерентности источника. Как и в случае некогерентного освещения, входная правая круговая поляризация приводит к проявлению негатива желаемого изображения.
Когда луч с линейной поляризацией направляется на волшебную пластину, а не с одной из круговых поляризаций, результирующее изображение представляет собой когерентную линейную комбинацию изображений, которые можно получить от левого и правого круговых входов. Более того, оптическая задержка волшебной пластины может быть изменена не на π, а на любые другие значения. На 4e и 4f показано, что настраивая оптическую задержку можно переключаться в заданной плоскости между распределением интенсивности входного луча и изображением, закодированным в пластине.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.
Эпилог
В рассмотренном нами сегодня труде ученые успешно реализовали волшебное зеркало и волшебную пластину (окно) на жидких кристаллах, использующую принцип управления светом с помощью плоской оптики, где фронт падающей световой волны модулируется неоднородным распределением показателя преломления.
Созданное устройство, состоящее из двух стекл из оксида индия-олова, покрытых полиамидом, позволяло получить либо изображение, либо его негатив в зависимости от входной круговой поляризации (левая или правая). Само изображение, а точнее его шаблон, было закодировано в полиамиде, покрывающем стекла устройства. При этом волшебная пластина может быть настроена для работы на различных длинах волн, так как ее оптическое запаздывание можно регулировать, прикладывая к пластине внешнее электрическое поле. Разработанное устройство было протестировано как при некогерентных, так и при когерентных источниках света. Во втором случае интерференционные эффекты приводят к образованию поляризационных особенностей (С-точек).
Ученые отмечают, что их творение основано на жидкокристаллических устройствах толщиной в несколько длин волн. Однако, как было доказано в других исследованиях, PBOE (оптические фазовые элементы Панчаратнама-Берри) могут быть реализованы и с диэлектрическими метаповерхностями толщиной меньше длины волны. Кроме того, существует возможность использования ахроматических и нечувствительных к поляризации метаповерхностей для формирования волшебных окон и дальнейшего снижения зависимости устройств от длины волны. Следовательно, результаты данного труда предполагают возможность уменьшения толщины плоских волшебных окон до субволновых масштабов.
Проделав столь сложную работу, ученые не собираются останавливаться на достигнутом и уже начали трудиться над новым детищем. Они решили использовать результаты рассмотренного нами исследования для создания квантовых волшебных пластин. Например, две такие пластины могут создавать запутанные изображения, которые можно использовать для изучения новых протоколов квантовой визуализации.
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?



