Приблизительно 31 января 1913 года, математик Г.Х. Харди, преподающий в Тринити-колледже Кембриджского университета, получил почтовую посылку из Мадраса, Индия.
Внутри была пачка бумаг и сопроводительное письмо, отправленное молодым индийским математиком по имени Сриниваса Рамануджан. Рамануджан был начинающим, но невероятно талантливым молодым математиком-самоучкой. В сопроводительном письме он обсуждал три темы, которые привлекли внимание Харди:
- Рамануджан представил интересные результаты, связанные с разложением чисел на сумму квадратов и их особенностями.
- Индиец предложил новые методы для вычисления различных рядов.
- Показал свои работы в области решения диофантовых уравнений.
❯ Сопроводительное письмо
Вступительный абзац, вероятно, был нужен для того, чтобы вызвать как жалость, так и удивление у Харди — ведущего английского математика своего времени.
Уважаемый сэр, Вам пишет клерк из бухгалтерии Портового трастового управления в Мадрасе с зарплатой всего 20 фунтов стерлингов в год. Мне сейчас около 23 лет. У меня нет университетского образования, я прошел обычный школьный курс*. Однако, по окончании школы, я начал уделять много времени изучению математики и самостоятельно нашел новые методы и идеи. Мои исследования сфокусированы на расходящихся рядах, и результаты, которые я получил, были признаны местными математиками как «поразительные».
*На самом деле, Рамануджан просто не обращал внимание на другие предметы, поэтому и провалил вступительные экзамены в Мадрасский университет. Индийские биографы придерживаются точки зрения, что поворотным моментом в жизни индийца было его знакомство с книгой «Конспект элементарных результатов по чистой и прикладной математике» Джорджа Шубриджа Кара. Имея её на руках, Сриниваса задался целью самостоятельно доказать 6165 теорем, представленных в ней только в виде формулировок. Сам Рамануджан по этому поводу говорил, что «формулы во снах ему являла богиня Намаккаль (богиня благополучия), и, вставая с кровати, он мог быстро записать результаты и проверить их, хотя и не всегда с доказательством».
❯ Второй абзац
Во втором абзаце Рамануджан подходит к сути своего вопроса:
Я обратил своё внимание на интегралы и различные суммы, которые привели меня к исследованию гамма-функции для отрицательных и дробных значений. Я получил некоторые новые и интересные результаты, которые, как я считаю, имеют важное значение. Я доказал некоторые из них, но всё же несколько вопросов остаются открытыми, и я был бы рад услышать ваше мнение.
Мои исследования направлены на придание значения второму интегралу Эйлера для всех значений n (точно так же, как в вводятся отрицательные и дробные показатели степени в элементарной математике). Мои друзья из университета, говорят мне, что
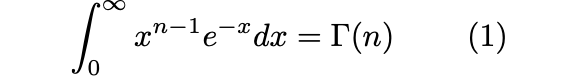
верно только тогда, когда n положительно. Они говорят, что это интегральное соотношение не имеет смысла, когда n отрицательно. При условиях, которые я излагаю в письме, интеграл верен для всех значений n, отрицательных и дробных. Все мои исследования основаны на этом, и я продвинулся до такой степени, что местные математики не в состоянии меня понять.
Гамма-функция Γ(n), на которую ссылается Рамануджан, стала объектом изучения с тех пор, как Бернулли и Гольдбах в 1720-х годах начали изучать факториалы дробных аргументов.
За 50 лет до Рамануджана уже было известно, что гамма-функция определена для всех комплексных значений z, которые больше нуля. Комплексные числа включают в себя действительную и мнимую части. Обозначим действительную часть комплексного числа как Re(z) (обычное вещественное число) и мнимую часть как Im(z). Таким образом, комплексное число можно записать как z = σ + it, где σ — действительная часть, а it — мнимая часть.
Чтобы использовать гамма-функцию Γ(z), ее обычно представляют в виде:
Гамма-функция обобщает понятие факториала на поле комплексных чисел. Она широко применяется в различных областях математики и физики. Рамануджан в своих исследованиях внёс значительный вклад в ее изучение, построив её т.н. аналитическое продолжение (внимание!), не имея никаких академических знаний и инструментов по его построению (термин «аналитическое продолжение» ввёл в 1842 году Карл Вейерштрасс. Рамануджан не был знаком с его трудами).
Пример формулы, которую показал Рамануджан в своем письме:
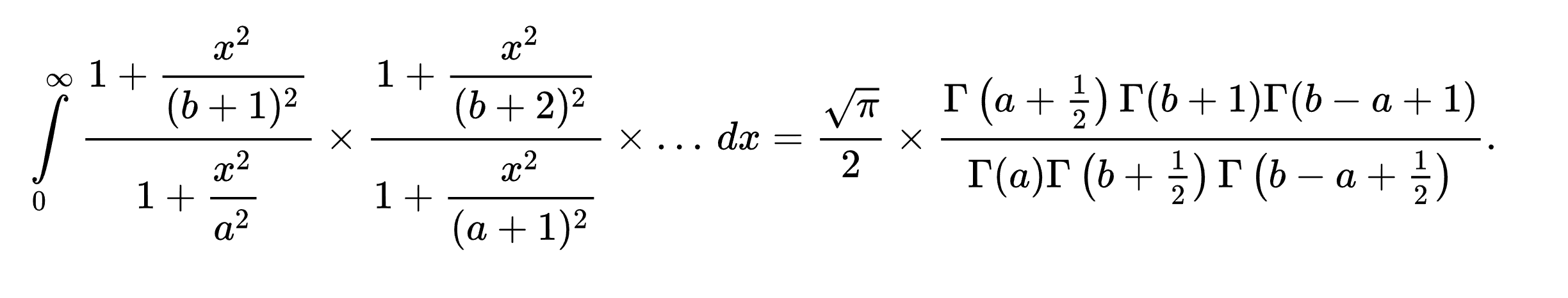
❯ Третий абзац
Недавно я читал одну из Ваших работ и на странице 36 обнаружил интересное утверждение. Вы утверждаете, что на данный момент нет точного выражения для количества простых чисел, меньших чем заданное число. Могу подтвердить, что вы нашли выражение, которое очень близко к реальному результату.
Количество простых чисел, которые меньше или равны заданному действительному числу x, обозначается как π(x) и представляет собой ступенчатую функцию, увеличивающуюся на 1 при каждом простом значении x. Ниже приведен график функции π(x) до x = 200:
π-функция даёт точно значение количества простых чисел, меньших данного. Однако, функциональная зависимость в общем виде не известна (всё упирается в справедливость недоказанной гипотезы Римана). Все существующие на данный момент зависимости — это суть приближения к π-функции.
Гаусс рассматривал вопрос о том, сколько простых чисел меньше заданного числа, когда ему было 15 или 16 лет в 1792-1793 годах. Лежандр немного позже, в 1797-98 годах предположил (на основе таблиц простых чисел Фелькеля и Веги), что π-функция аппроксимируется выражением:
где A и B — некоторые константы. Позже он показал, что приближенное значение A = 1, B = -1.08366. Дальнейшие приближения π-функции основываются на теореме о распределении простых чисел, которая утверждает, что, если x стремится к бесконечности, то π (x) стремится к x / ln (x):
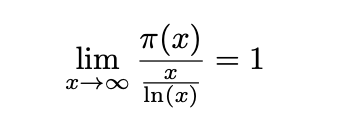
Другими словами, для достаточно больших х графики указанных выше функций будут сливаться в один:
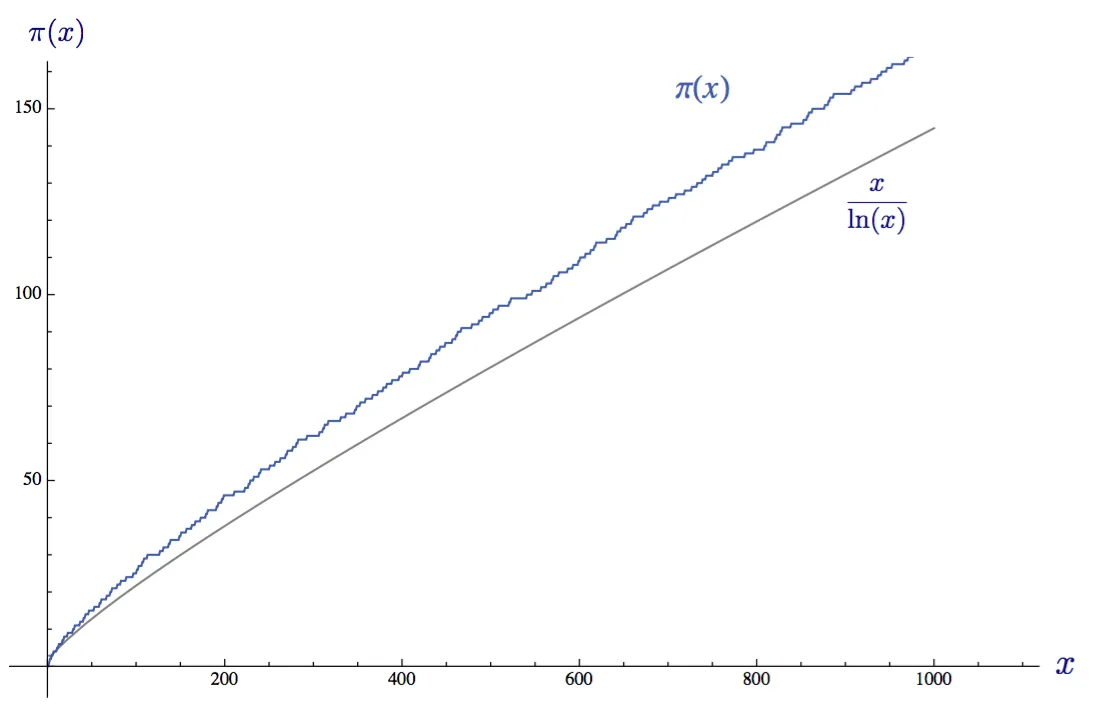
Позже Дирихле сформулировал свое собственное приближение:
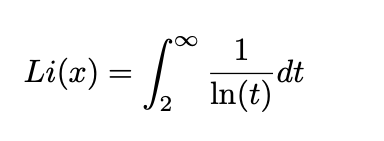
Оказывается, что Li (x) на самом деле является лучшим приближением к π-функции , чем x / ln(x):
Заявленные в письме Рамануджана приближения были гораздо менее точным, но все же удивительными, учитывая его ограниченный доступ к современным работам. Пример одного из выражений:
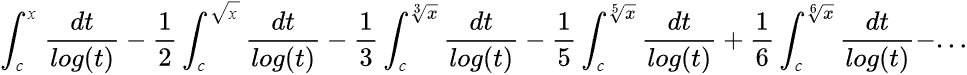
Т. е. количество простых чисел, меньших х, аппроксимируется формулой выше, при c = 1,45136380. Обратите внимание на то, как устроен ряд. Он не является знакопеременным, а знак его слагаемых определяется в соответствии с функцией Мёбиуса:
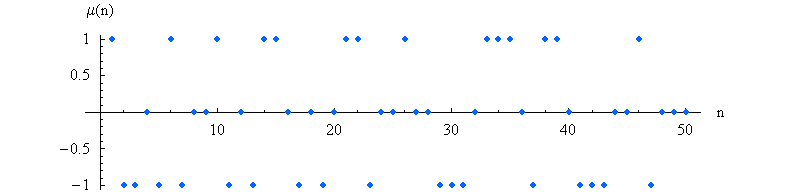
Именно поэтому в формуле пропущена 1/4 и знак меняется на положительный при 1/6. Короче говоря, это очень не тривиальный результат, который не мог не остаться без внимания.
❯ Четвертый абзац
Будучи бедным, но уверенным в ценности своих идей, я стремлюсь опубликовать свои теоремы. Хотя я не представил конкретных исследований или выражений, которые я получил, я указал направления, в которых продолжаю работать. Я очень ценю любой совет, который вы можете мне дать. Прошу прощения за возможное беспокойство. С уважением, Дорогой сэр, Искренне ваш, С. Рамануджан
На страницах, следующих за этим коротким сопроводительным письмом Рамануджан представил еще минимум 11 страниц (две из которых, к сожалению, теперь утеряны), содержащих технические результаты по бесконечным рядам (в т.ч. расходящимся), гамма-функции, распределению простых чисел, гипергеометрическим функциями, цепным дробям, эллиптическим функциям, числам Бернулли и многое другое. Вот лишь некоторые выражения, которые были представлены в письме:
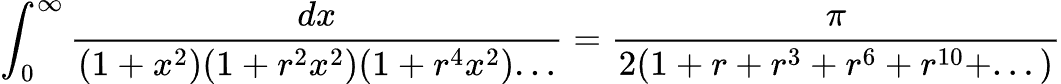
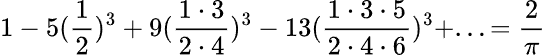
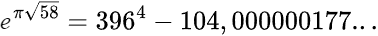
❯ Реакция Харди
Письмо Рамануджана станет первым в долгой переписке, кульминацией которой станет приглашение индийцу приехать в Тринити-колледж в Кембридже, чтобы работать с Харди.
Но, получив первое письмо Рамануджана, Г. Х. Харди сначала отнесся к нему скептически.
Как описывает Роберт Канигель в своей книге «Человек, познавший бесконечность» (1991), страницы с теоремами Рамануджана показались Харди странными: всё было вроде знакомо и понятно, но изложение было совершенно непредсказуемым, часто опирающимся на интуицию. Харди думал, что индиец просто еще один чудак или мошенник.
Однако, письмо индийца все равно не давала ему покоя. Некоторые «странные теоремы», как минимум, вызывали любопытство, ведь Харди раньше не сталкивался с ними и не подозревал о их существовании.
Когда через некоторое время Харди снова обратил внимание на рукопись Рамануджана и увидел его теорему о цепных дробях на последней странице, его впечатление диаметральное изменилось. Харди попросил своего коллегу Дж. Э. Литтлвуда прочитать эту теорему, и его реакция была точно такой же – изумление гениальностью Рамануджана.
В дальнейшем Харди скажет, что письмо Рамануджана было безусловно, самым замечательным из всех, которые я получал, и что Рамануджан был математиком высочайшего качества, человеком совершенно исключительной оригинальности и силы.
И добавит: Они (результаты) должны были быть истинными, поскольку если бы они не были истинными, то ни у кого не хватило бы воображения, чтобы изобрести их.
Бертран Рассел (1872-1970) позже написал, что на следующий день он нашел Харди и Литтлвуда в состоянии невероятного возбуждения, потому что они верили, что нашли второго Ньютона.
❯ Ответ Харди
Я с большим интересом прочитал ваше письмо и изложенные в нем теоремы. Однако, чтобы должным образом оценить вашу работу, мне было бы важно увидеть доказательства некоторых ваших утверждений. По моим наблюдениям, ваши результаты можно разделить примерно на три класса:
- Некоторые из ваших теорем уже известны или могут быть выведены из известных теорем.
- Есть результаты, которые, возможно, новы и интересны, но вызывают только любопытство.
- Ряд удивительных результатов, справедливость которых полностью зависит от строгости используемых вами методов доказательства.
Я очень надеюсь, что вы предоставите мне несколько доказательств как можно скорее и расскажете более подробно о вашей работе с простыми числами и расходящимися рядами. Считаю, что вы проделали большую работу и заслуживаете публикации. Если вы предоставите строгие доказательства, я с радостью Вам помогу.
Я не упомянул некоторые из ваших результатов, в частности о эллиптических функциях, так как передал их более опытному специалисту. Надеюсь получить от вас скорый ответ.
С уважением, Г.Х. Харди
Больше информации, о мнении Харди относительно таланта Рамануджана можно прочесть в замечательной книге «Двенадцать лекций о Рамануджане».
❯ Что было дальше
В 27 лет Рамануджан переедет в Англию и начнет работу в Кембриджском университете в должности профессора математики на базе только лишь школьного образования. Рамануджан создаст свой уникальный математический мир, объединяя начальный запас математических фактов с огромным количеством наблюдений над конкретными числами. Здесь уместно вспомнить классическую историю про число 1729.
❯ 1729
Эту история рассказал сам Харди в книге «Апология математика». Навещая в больнице Рамануджана, он пожаловался, что приехал на скучном и не примечательном такси с номером 1729. Рамануджан же воскликнул на это:
А ведь 1729 — это наименьшее натуральное число, которое можно представить в виде суммы кубов двумя различными способами!
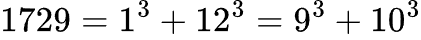
С тех пор число 1729 официально называется числом Харди-Рамануджана. Действительно, это лучшая иллюстрация слов Харди, что каждое натуральное число становилось личным другом Рамануджана, так быстро и легко он работал с ними.
❯ Потерянная записная книжка Рамануджана
Это рукопись, в которой Рамануджан записал математические открытия последнего года (1919-1920) своей жизни. Ее местонахождение было неизвестно до 1976 года, пока она не была найдена в старой коробке в библиотеке Тринити-колледжа в Кембридже. Рукопись состоит из «139 листов, исписанных с двух сторон характерным почерком Рамануджана» и содержит более шестисот математических формул, перечисленных последовательно (!!!) без доказательств. В дальнейшем практически все формулы были доказаны, что было отражено в четырех увесистых книгах.
Один из авторов этих книг американский математик Брюс Брендт сказал:
Обнаружение этой рукописи вызвало примерно такой же переполох в математическом мире, какой вызвало бы открытие десятой симфонии Бетховена в музыкальном мире.
Самая важная находка в рукописях Рамануджана — это его взгляд на теорию модульных форм. Рамануджан ввёл т.н. «ложные тета-функции» — выражения вида:
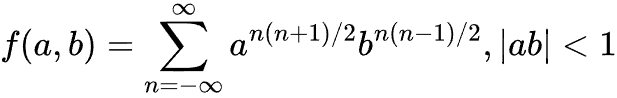
Оказалось, что эти функции можно использовать для анализа химических процессов в полимерах и даже вычисления энтропии черных дыр. Остальная часть записок посвящена очень широкому спектру математических проблем:
- функциям Бесселя;
- константе Эйлера-Маскерони;
- диофантовым приближениям;
- гипотезе Римана;
- рядам Фурье;
- преобразованию Лапласа.
Кроме того, рукопись содержит огромное количество решенных задач, связанных с бесконечными рядами и интегралами. Согласитесь, внушительный список!
❯ Индийское чудо
Рамануджан обладал поистине нечеловеческой интуицией, работоспособностью и уникальным незамыленным взглядом, который позволял творить чистое искусство. Посмотрите на ту формулу:
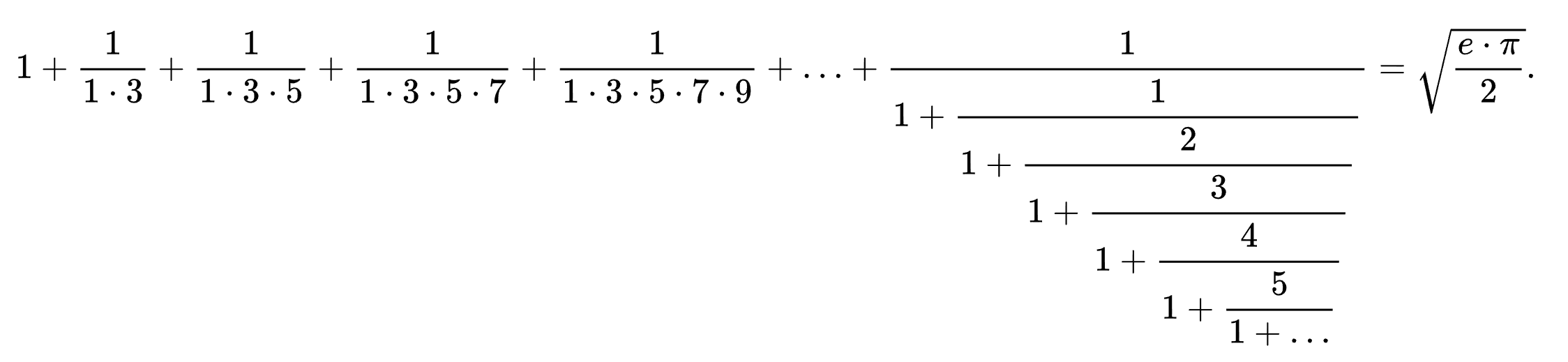
и на удивительную формулу для числа π:
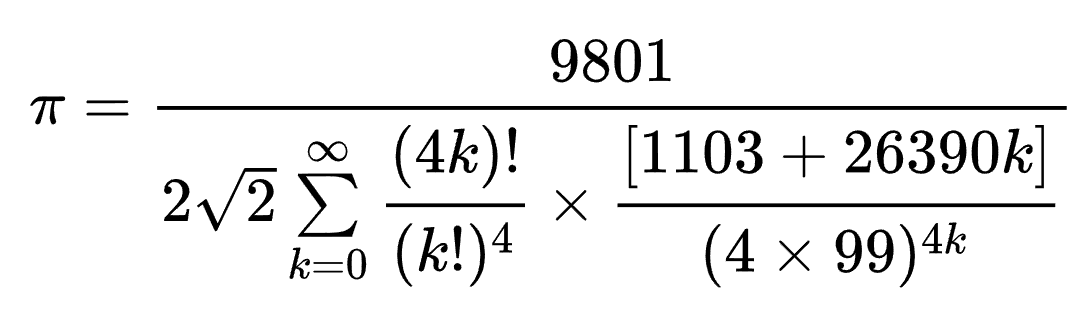
Тысячами граней математической красоты заиграли бесконечные радикалы:
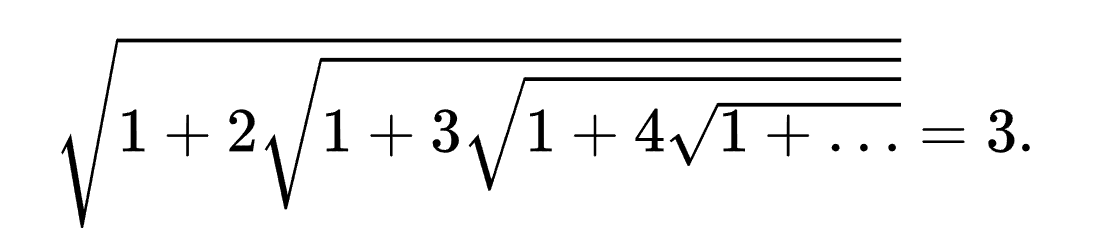
Многие современники справедливо считали Рамануджана чудом, опережающим свое время не менее, чем на сто лет. Его проницательность и гениальность поражали. И сейчас люди не перестают удивляться его таланту, который позволял ему преодолевать границы математического знания своего времени.
По семейным обстоятельствам Рамануджан вернется в Индию, где умрет в возрасте 32 лет 26 апреля 1920 года. Причиной его преждевременной смерти, возможно, стал туберкулез, осложненный недоеданием, истощением и стрессом. Однако, в 1994 году появилось предположение о том, что у Рамануджана могла быть амёбная дизентерия. В мировой науке он останется навеки примером, с одной стороны, исключительной гениальности, а с другой — нереализованного потенциала.
Больше математики в Telegram — «Математика не для всех».
Возможно, захочется почитать и это:
- ➤ Удивительные клеточные автоматы: клетки-киллеры, BSFK[L]
- ➤ Инопланетная математика
- ➤ 113 лет со дня рождения Конрада Цузе – всемирно признанного изобретателя компьютера
- ➤ «Странная алгебра», философия упрощения и изобретение бита. К 107-летию со дня рождения Клода Элвуда Шеннона
- ➤ Big data. Математика на службе биологии
