Вводная информация
Термин full reptend prime применяется к простому числу P в некоторой системе счисления base, в случае если число 1/P может быть представлено в виде бесконечной периодической дроби, длина периода которой будет равна P — 1.
Для любого простого числа P, существует бесконечное множество систем счисления в которых данное P является full reptend. Данные системы счисления распределены в соответствии с паттерном, уникальным для каждого числа P.
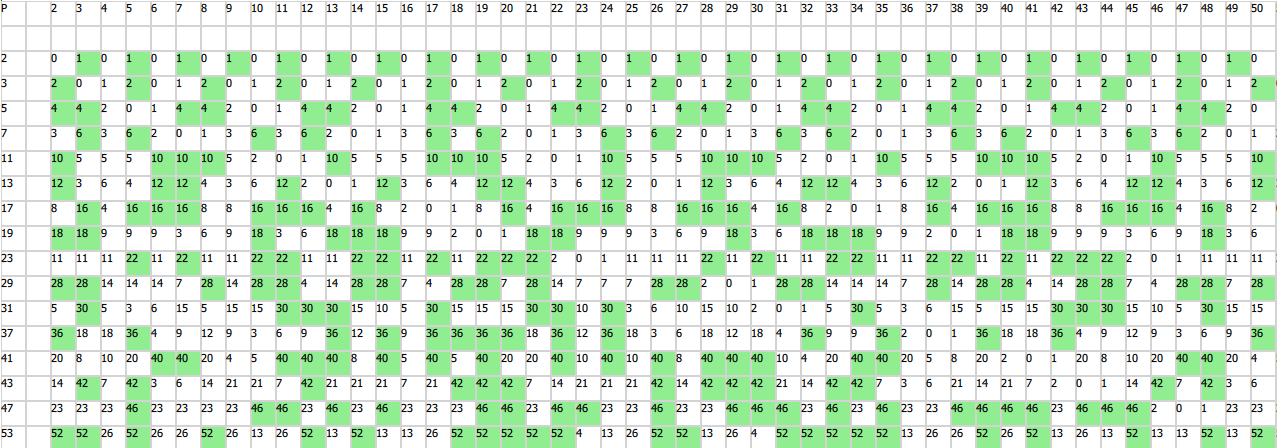
В таблице строки соответствуют простым числам, а столбцы системам счисления. В каждой ячейке отображена длина периода бесконечной периодической дроби 1/P. Зелеными ячейками выделены позиции соответствующие определению full reptend prime. Для каждого простого числа длина паттерна равна P.

Системы счисления в которых невозможны full reptend
Визуально заметна закономерность: для всех простых чисел P >= 3, не существует full reptend в системах счисления, которые являются квадратами натуральных чисел.
Для P = 2 full reptend позиция будет встречаться в системах счисления, которые являются квадратами нечетных чисел.

До визуализации таблицы выше, я предполагал что количество full reptend позиций увеличивается или остаётся равным при росте P. Однако это оказалось не так: для P = 17 существует 8 позиций, а для P = 19 всего 6.
Выписав количество позиций для первых 9 простых чисел, я получил: 1, 1, 2, 2, 4, 4, 8, 6, 10. В OEIS я нашёл последовательность, которая описывала искомую мной закономерность.
Вывод из найденной последовательности: для того чтобы получить количество full reptend позиций для простого числа P, требуется получить значение функции Эйлера в точке P-1, т.е. phi(P-1).
Схожим методом я осуществил попытку найти последовательность, описывающею паттерны full reptend позиций. Для первых 6 простых чисел у меня получилось: 1, 2, 2, 3, 3, 5, 2, 6, 7, 8, 2, 6, 7, 11. Успешно нашлась соответствовавшая последовательность. Интересно отметить, что P = 2 было отведено в унарную систему счисления.
Вывод из найденной последовательности: для того чтобы определить структуру паттерна full reptend для исследуемого числа P, необходимо найти все первообразные корни по модулю P, для чисел меньше P.
Необходимые условия первообразного корня.
Первообразный корень g по модулю m должен соответствовать двум условиям, заданных формулами иже:
Рассмотрим по подробнее каждое из условий:
-
Поскольку число m будет всегда простым, а функция Эйлера в точках соответствующих простому числу P, будет равна P — 1 мы можем переписать данное условие:
-
Схожим образом можно переписать значение l:
Проверка чисел 2 и 3, на возможность выступать первообразным корнем по модулю 7.
Рассмотрим g = 2.
Т.к. 26 mod 7 = 1, первое из двух условий выполнилось. Теперь необходимо проверить оставшиеся 5 условий:
-
2 mod 7 = 2
-
4 mod 7 = 4
-
8 mod 7 = 1
-
16 mod 7 = 2
-
32 mod 7 = .
Условие номер 3 не было выполнено, т.е. среди l нашлось такое l = 3, когда xl mod m равно 1.
Рассмотрим g = 3:
Т.к. 36 mod 7 = 1, первое условие выполнилось
Теперь рассмотрим 5 оставшихся условий:
-
3 mod 7 = 3
-
9 mod 7 = 2
-
27 mod 7 = 6
-
81 mod 7 = 4
-
243 mod 7 = .
Все условия выполнились! Из этого следует, что 3 является первообразным корнем по модулю 7.
Симметрия структур периодических дробей
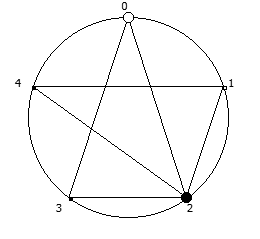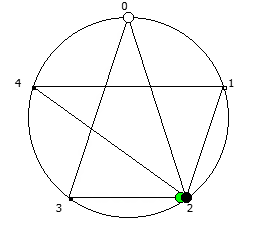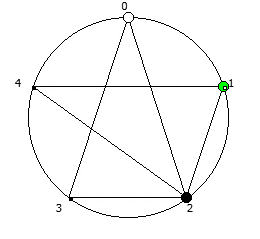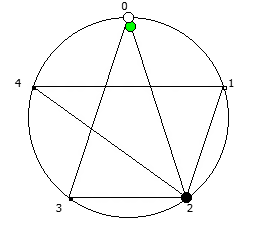
Для P >= 5 количество full reptend позиций всегда будет кратно 2. При этом любая структура периодической дроби в некоторой full reptend позиции, будет иметь свое симметричное отображение в другой full reptend позиции.
Данную закономерность удобнее всего визуализировать при помощи анимации. Внутри двух визуально похожих паттернов будет осуществляться движение в противоположную сторону.
Рассмотрим P = 5:
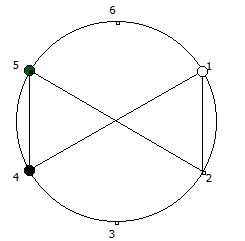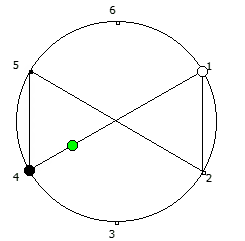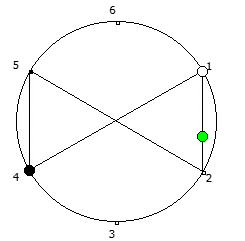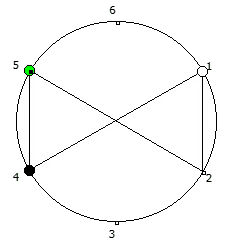
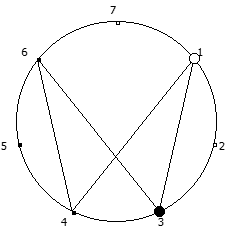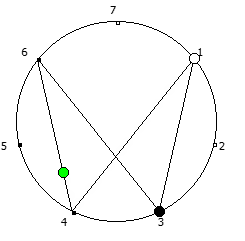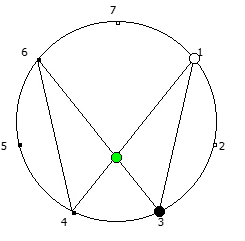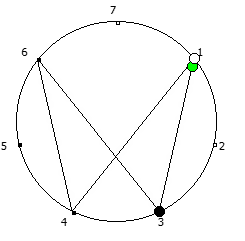
Рассмотрим P = 7:
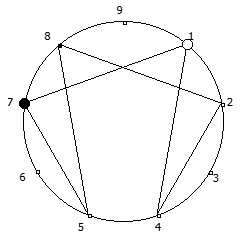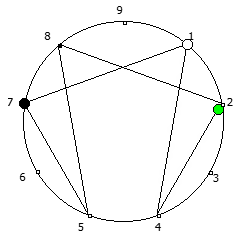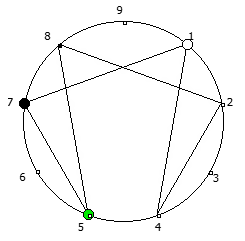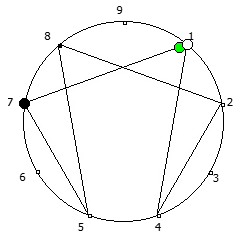
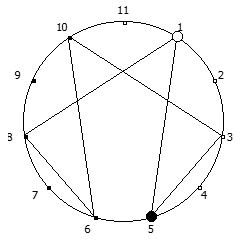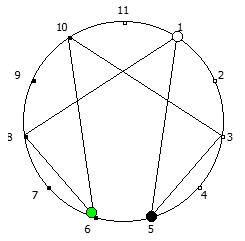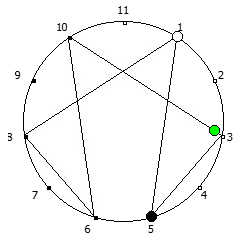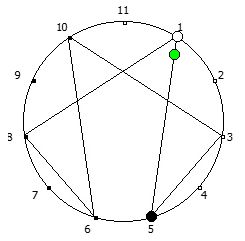
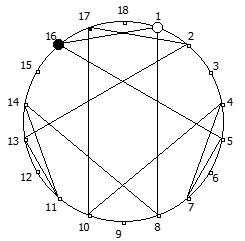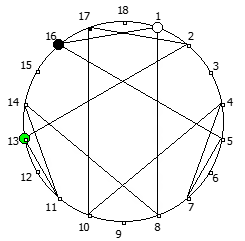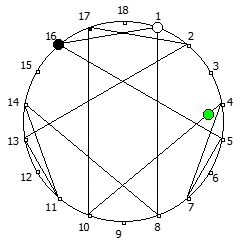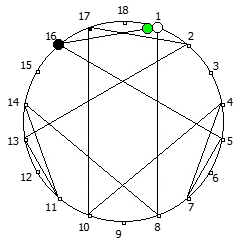
Рассмотрим P = 11:
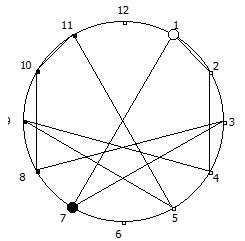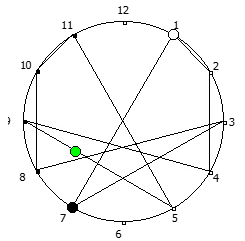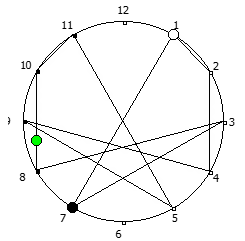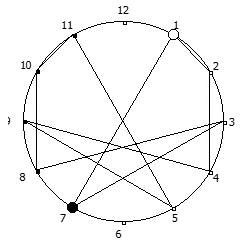
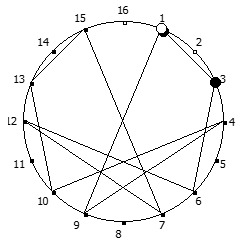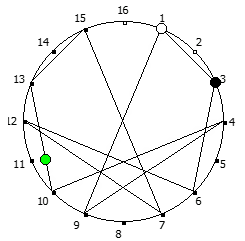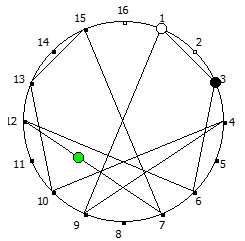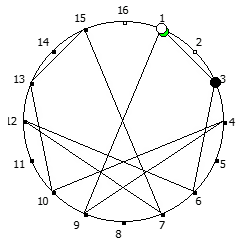

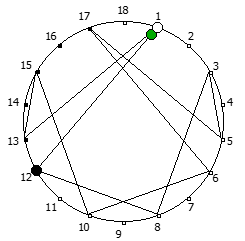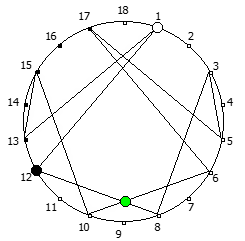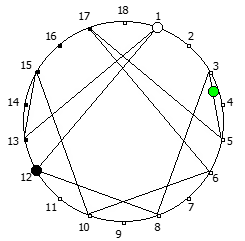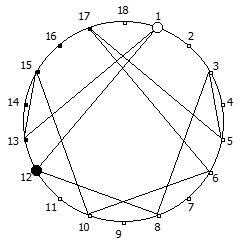
И последний пример, для P = 13:
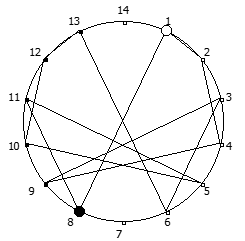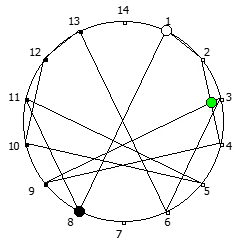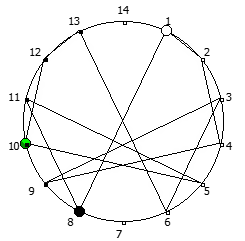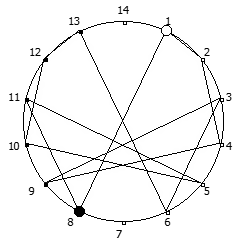

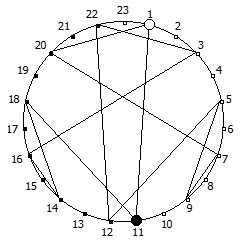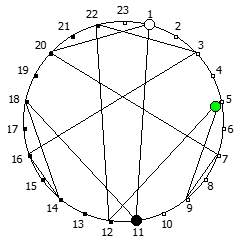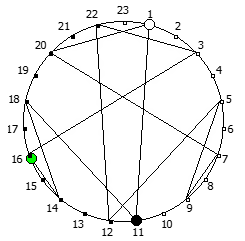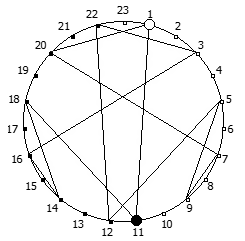
Уроборическая связь
Данная закономерность названа в честь мистического змея уробороса пожирающего свой хвост. Причина такого названия кроется в визуальной закономерности.
Суть этой закономерности сводится к 2-м фактам:
-
Для того чтобы визуализация периодической дроби 1/P была симметрична в системе счисления base требуется.
-
Если base < P, тогда цифры 0 и base - 1 помещаются на отдельные позиции, такое размещение я назвал не-уроборичны.
-
Если base > P, тогда цифры 0 и base — 1 помещаются на одной позиции (от сюда и название, змея пожирающего свой хвост), такое размещение я назвал уроборичным
-
-
Первая full reptend позиция с уроборичным размещением визуально идеально сочетается с full reptend позицией не-уроборичного размещения, если разница между системами счисления равна P.
Стоит отметить, что в системе счисления base = P не могут быть full reptend позиций.
Рассмотрим P = 5:
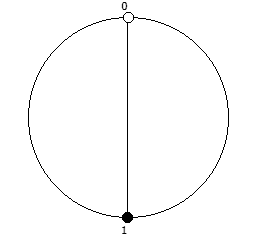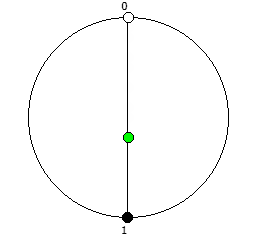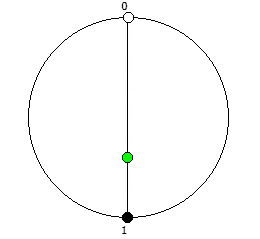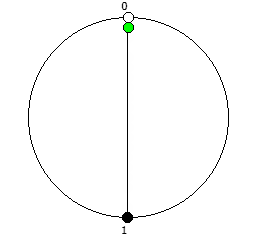
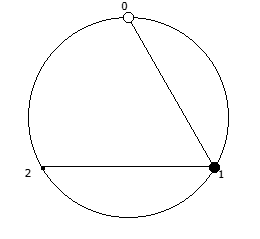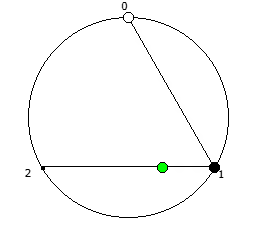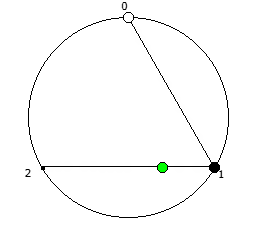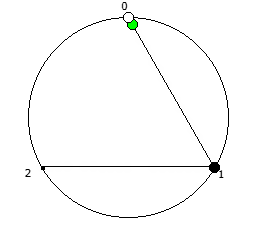
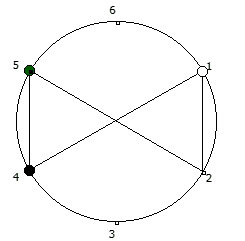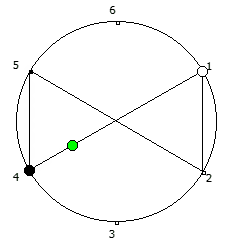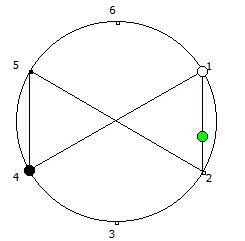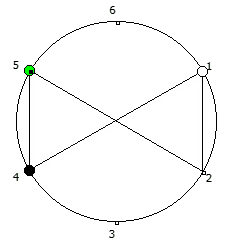
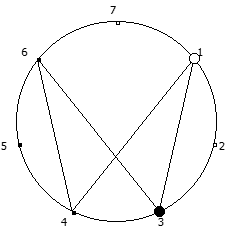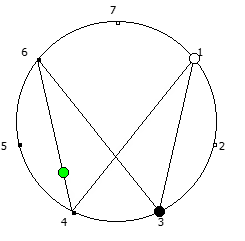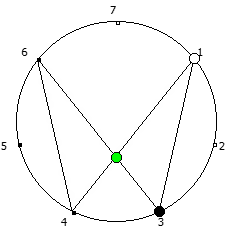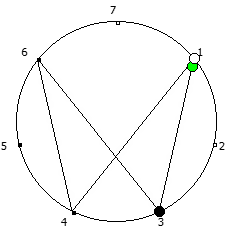
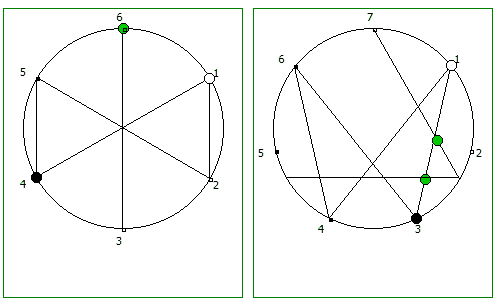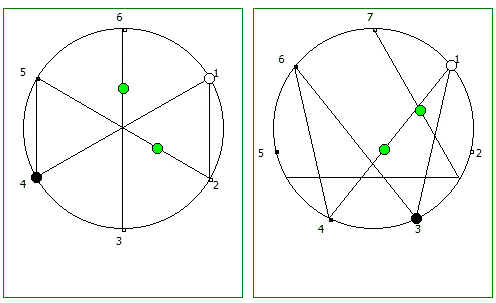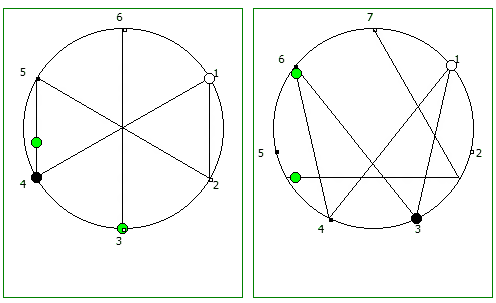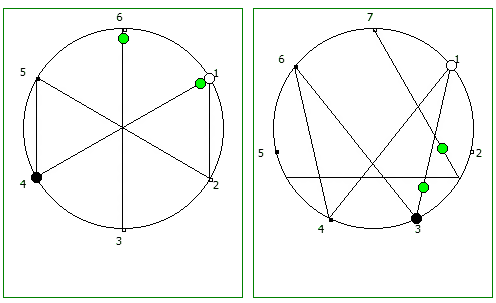
Рассмотрим P = 7:
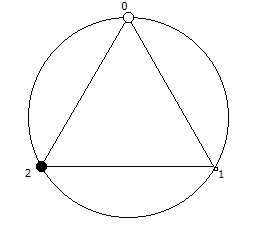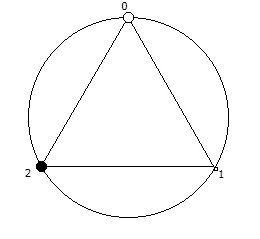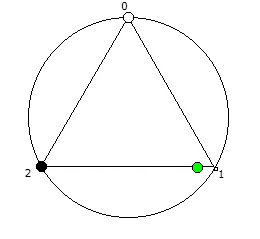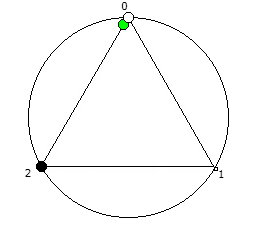
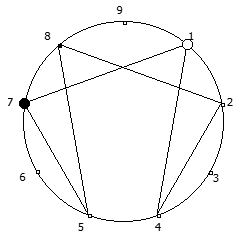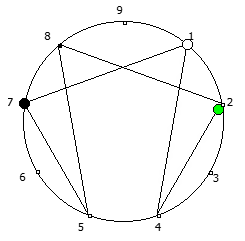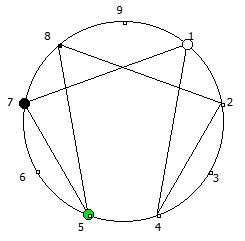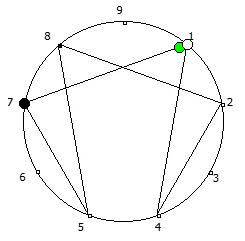
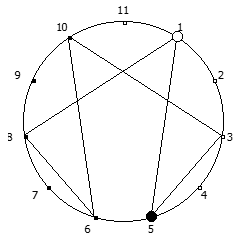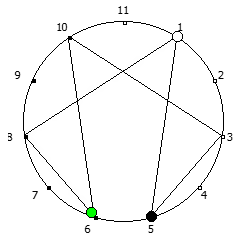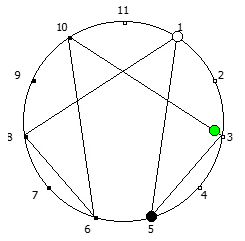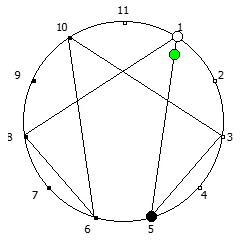
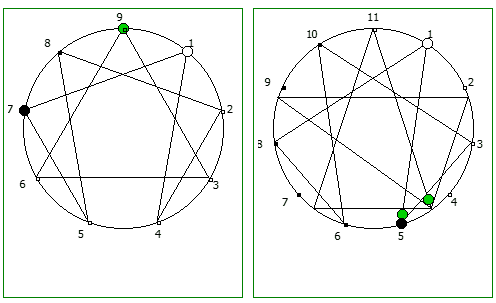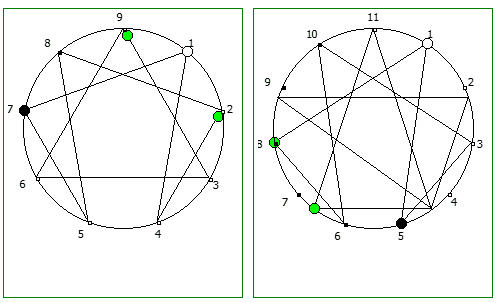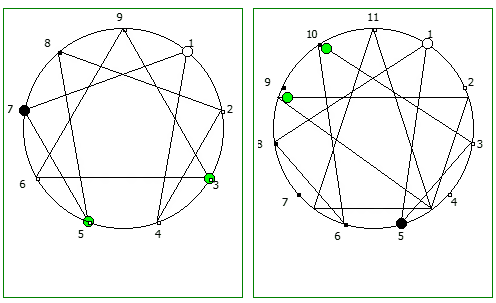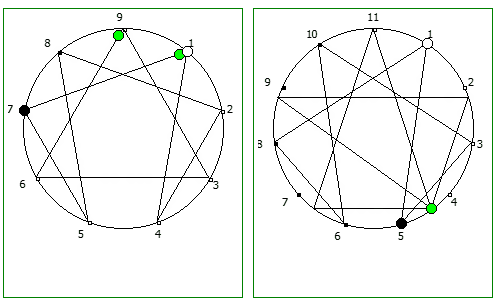
Рассмотрим P = 11:
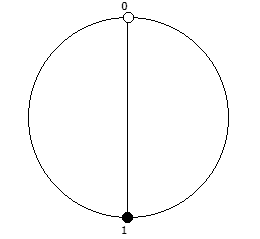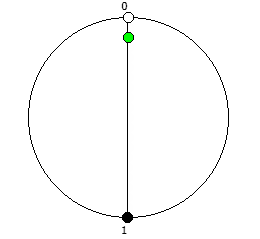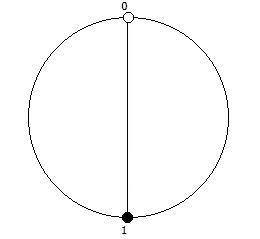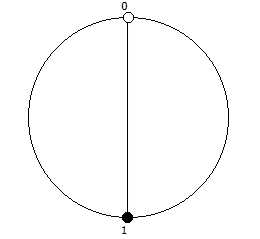
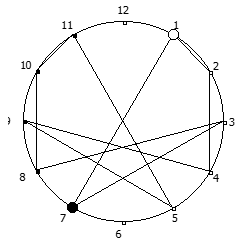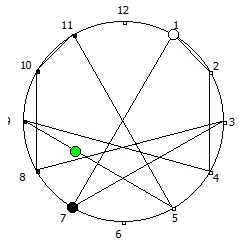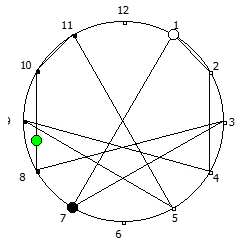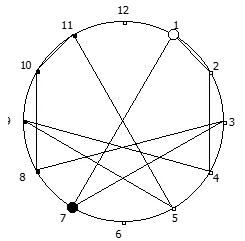
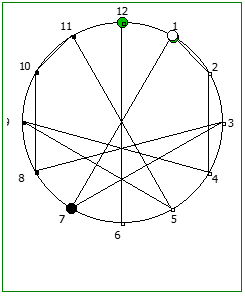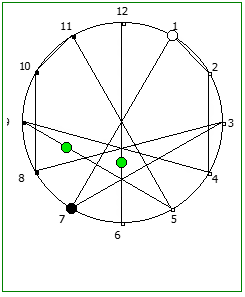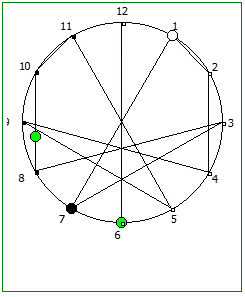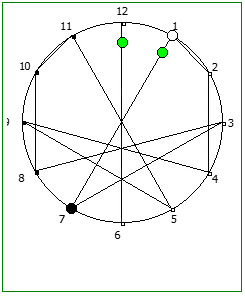
Рассмотрим P = 13:
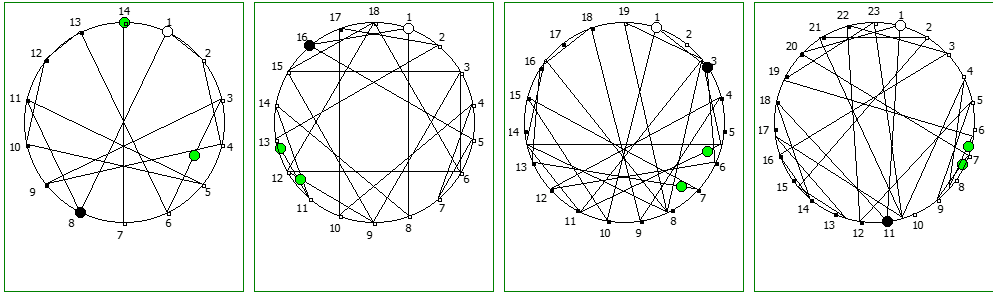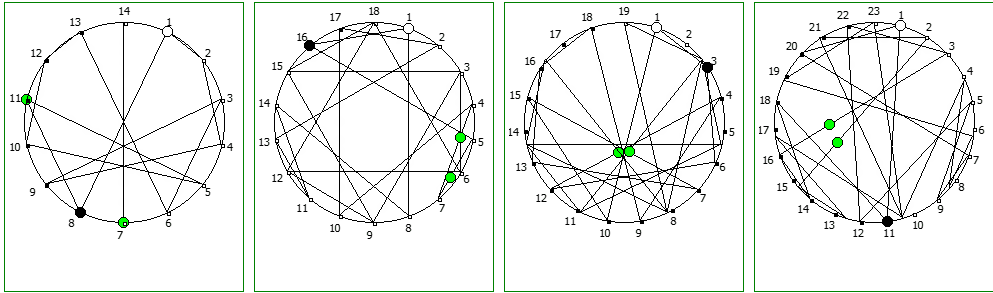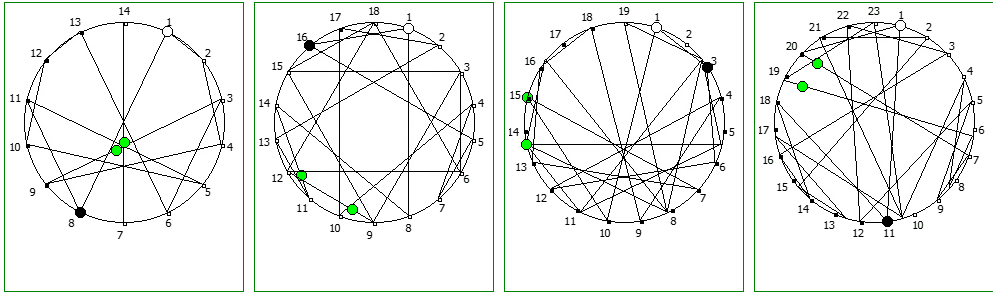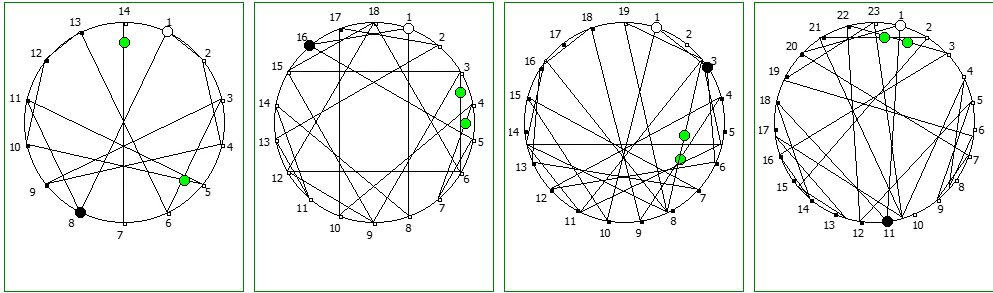
И последним рассмотрим P = 17:
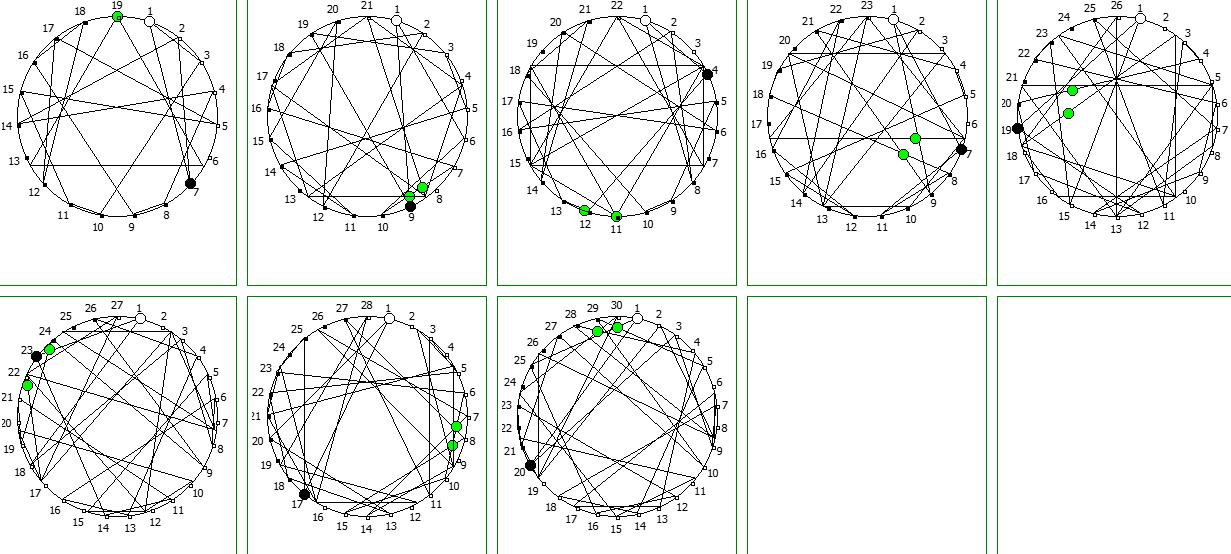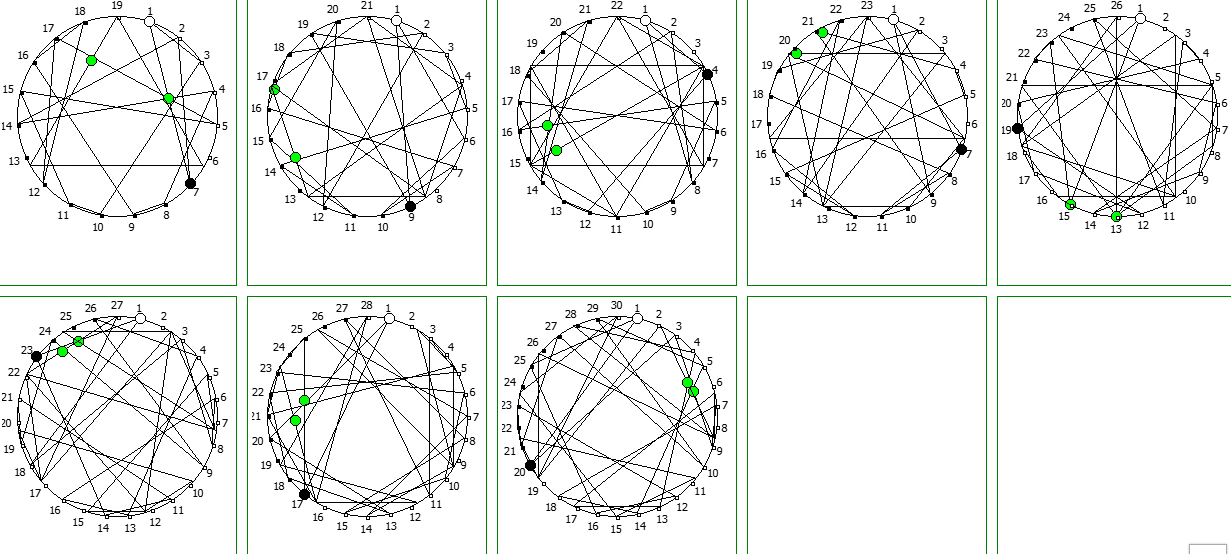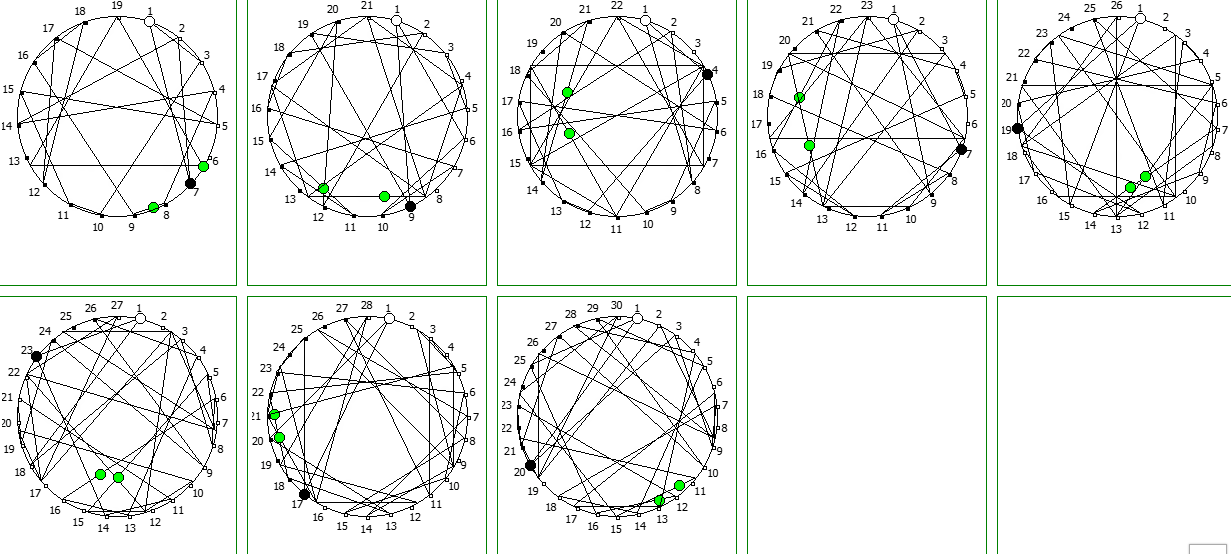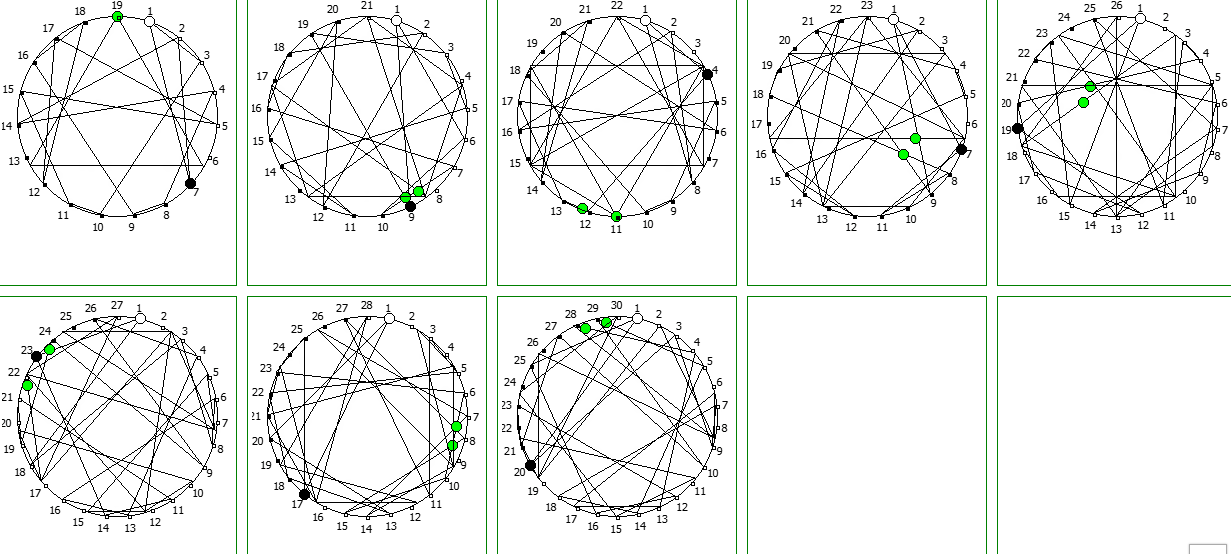
Структуры c не-уроборическом размещение являются «свернутыми», т.к. находятся в системе счисления, которая не может отобразить паттерн целиком. Но во всех последующих уроборических размещениях структура паттерна выглядит идентично.
Реверсированные периодические дроби
В один момент, мне стало любопытно: при помощи какой операции я мог бы получить из дроби 0.(142857) дробь 0.(758241).
Для того чтобы получить периодическую дробь в системе счисления base необходимо разделить число ожидаемое как период, на repunit соответствующей длины умноженный на base — 1.
Для того чтобы получить периодическую дробь 0.(758241) я разделил 758241 на 999999. Если сократить эту дробь, то получится: 3 * 23 / 7 * 13, или 69/91. Т.е. мне понадобилось умножить 1/7 на 69/13, чтобы развернуть порядок цифр.
При исследовании дробей от 1/91 до 90/91 я увидел, что в этом диапазоне находятся как все дроби от 1/7 до 6/7 и их реверсированные паттерны, так и все дроби от 1/13 до 12/13 с их реверсированными паттернами.
Для того чтобы увидеть немного больше об этой закономерности, разложим циклические числа на простые множители:
Циклическое число полученное от 1/7 = 142857 = 33 * 11 * 13 * 37,
Циклическое число полученное от 1/13 = 76923 = 33 * 7 * 11 * 37,
Знаменатель для получения периодической дроби = 999999 = 33 * 7 * 11 * 13 * 37.
Как можно видеть, знаменатель для получения периодической дроби отличается от циклических чисел на простые числа 7 и 13 соответственно.
Для получения реверсированных дробей простые числа могут комбинироваться не только парами: бывают случаи когда простое число комбинируясь с самим собой создает реверсированные дроби, например для P = 5. Или когда требуются использовать 3 простых числа, например для P = 17.
Спектр числа
Когда я приступил к исследованию темы full reptend prime — я ввел несколько собственных понятий, которые мне помогали систематизировать наблюдаемые явления. Одним из таких понятий был «спектр числа», который представлял собой массив с количествами использования каждой цифры. Например, для числа 41234 его спектр числа в десятичной системе счисления будет равен [0, 1, 1, 1, 2, 0, 0, 0, 0, 0].




Можно заметить общую закономерность, числа 1/17, 1/47, 1/97 генерируют спектр числа похожий на 1/7, с одним только отличием — к каждой из «корзин» спектра добавляется число десятков. Т.е. в случае с 1/17 это равномерное увеличение спектра на 1, в случае с 1/47 на 4, и в случае с 97 на 9 соответственно.
Сонификация
Мне было интересно исследовать закономерности не только при помощи глаз, потому я написал немного кода, который позволял их сонифицировать. Большое число сонификаций оказались не слишком гармоничными, но хочу привести два примера, которые звучат на мой взгляд неплохо.
Первой рассмотрим сонификацию 1/7 в 24 системе счисления. Для музыкальности добавлена простая гармонизация мелодии.
TheOutloud — платформа для коротких аудиоблогов и подкастовtheoutloud.ru
Следом идёт сонификация 1/36 в 23 системе счисления. Так же применена гармонизация.
TheOutloud — платформа для коротких аудиоблогов и подкастовtheoutloud.ru
Из-за паттернов циклических чисел, структура мелодии получается ломанной, похожей на математический рок.
Много визуализаций
Для начала я хочу поделиться несколькими красивыми визуализациями периодических дробей.
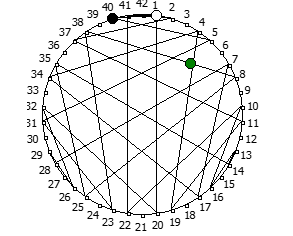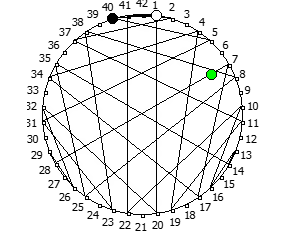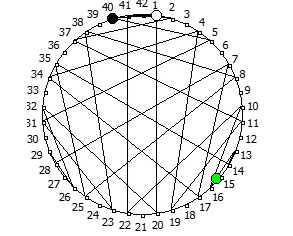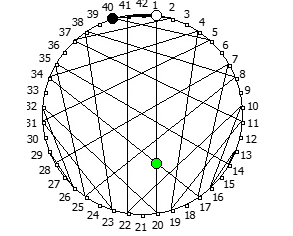
Некоторые из дробей образуют кардиойду:
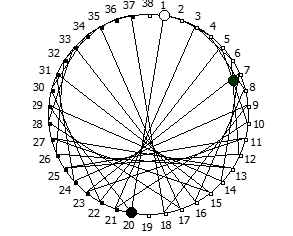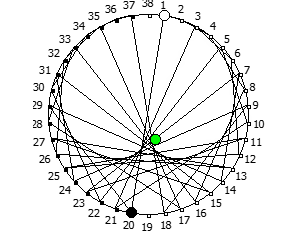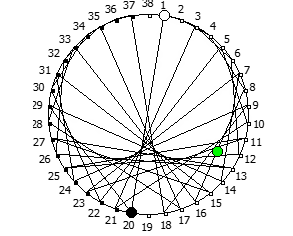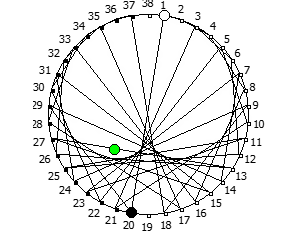
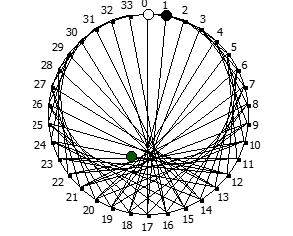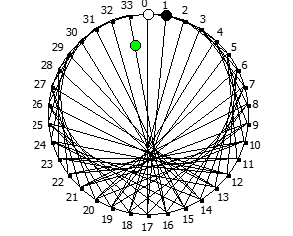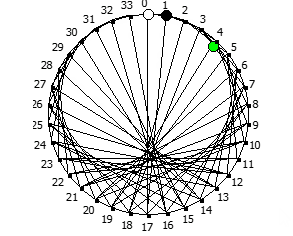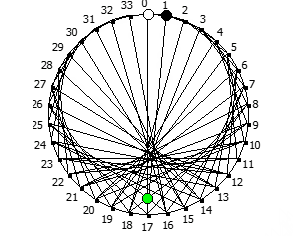
Другой интересный метод — визуализация одновременно всех периодических дробей образованных диапазона рациональных чисел от 1/N до N-1/N, где N это натуральное число.
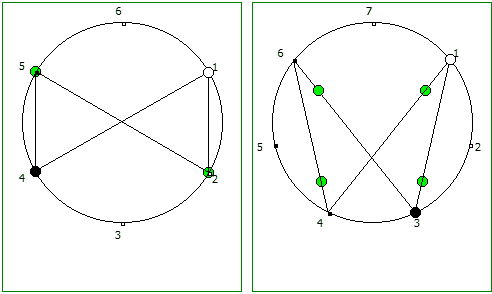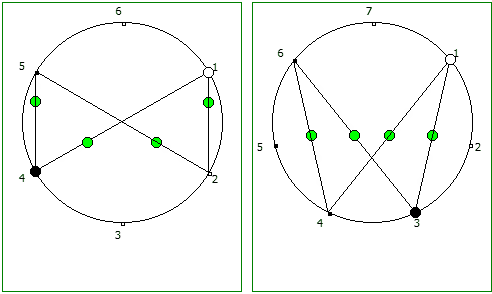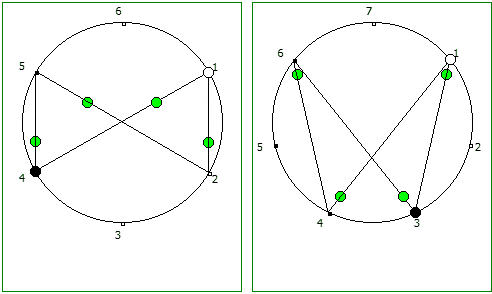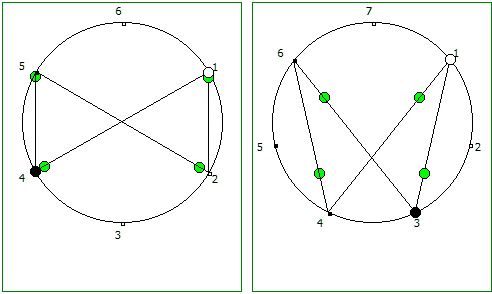
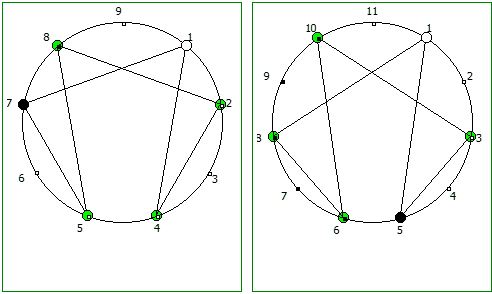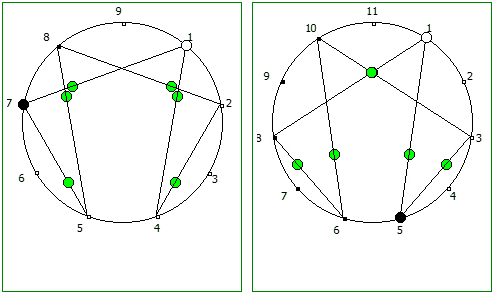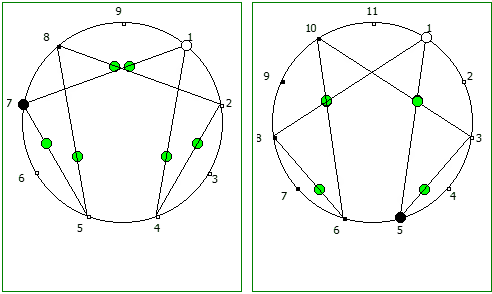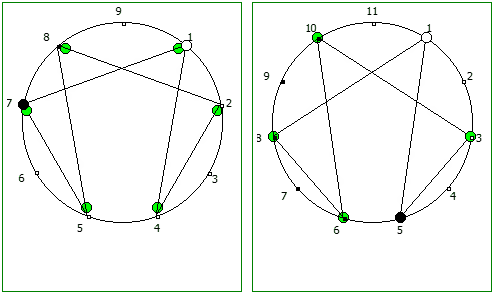
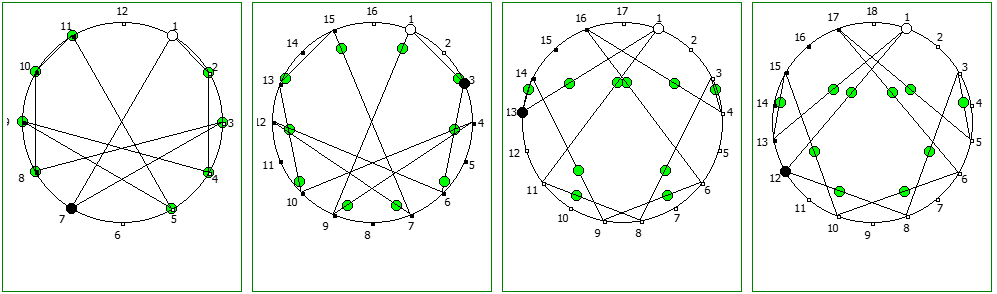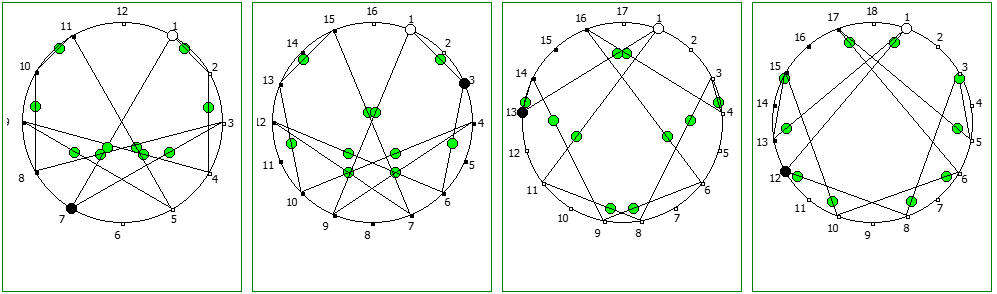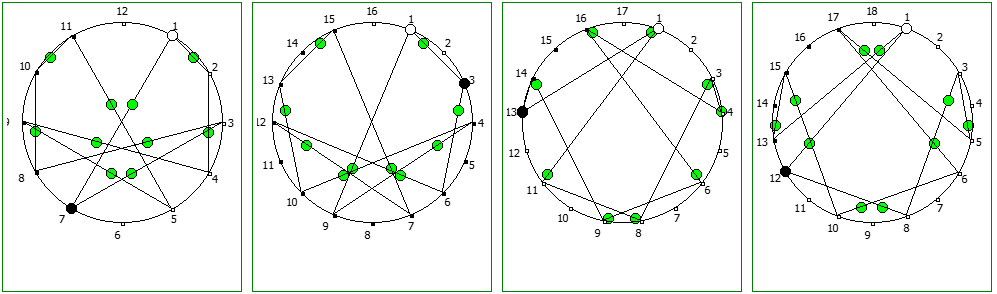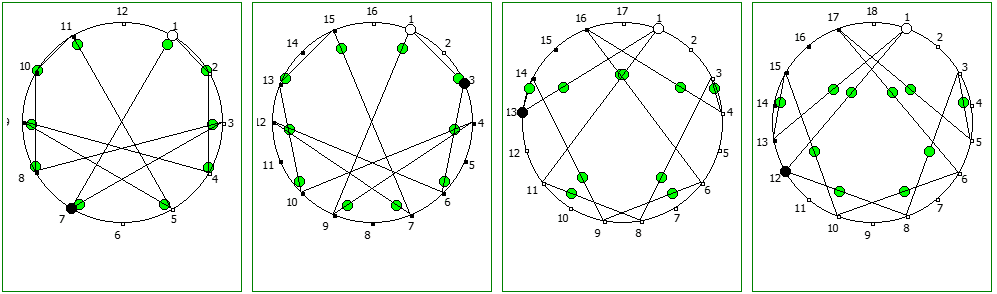
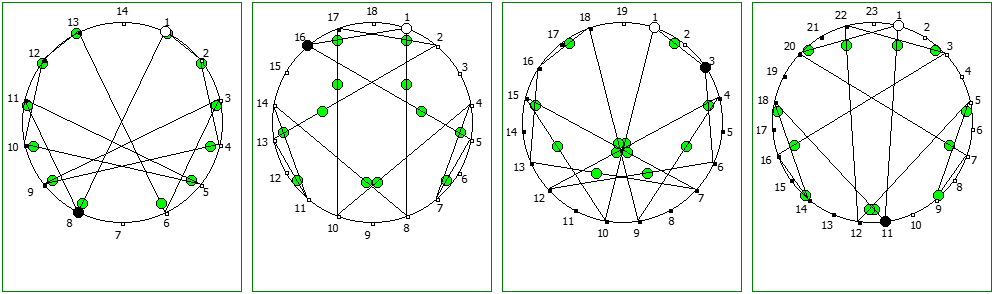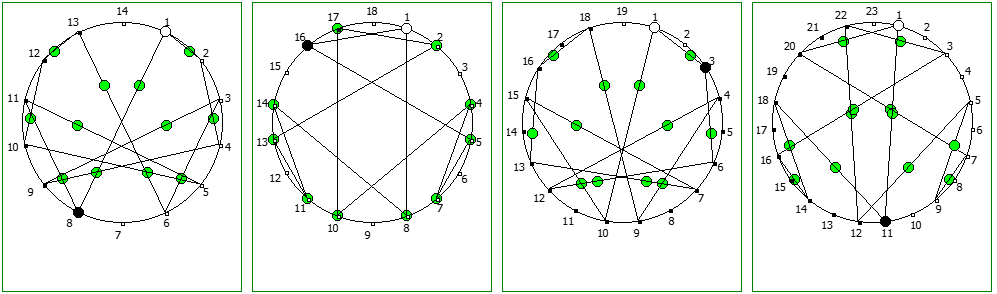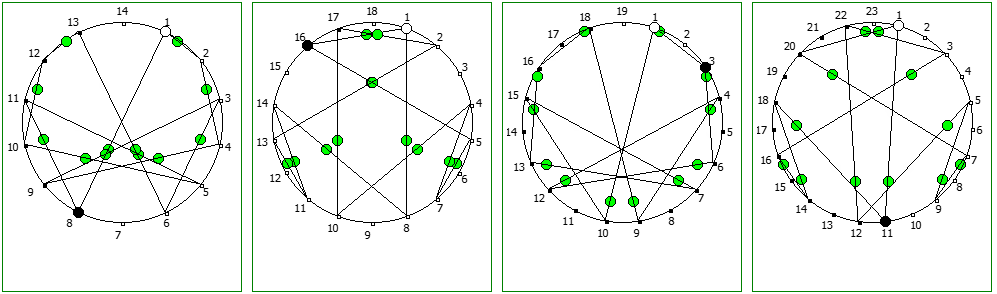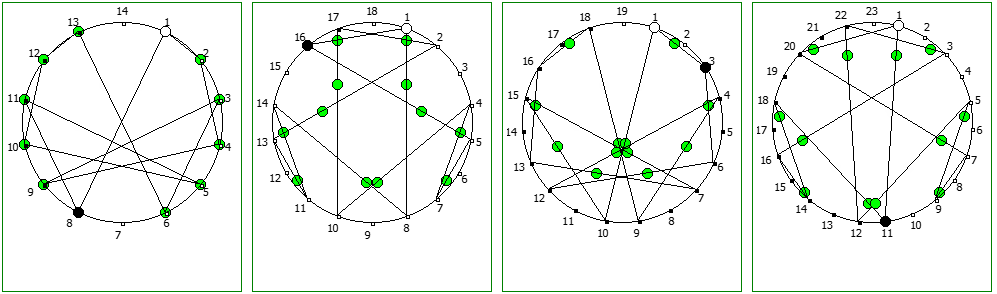
Подобные визуализации возможны и для простых чисел, которые не находятся в full reptend позиции, т.е. на диапазоне 1/P .. P-1/P образующих несколько разных паттернов (периодических дробей имеющих разные спектры числа).
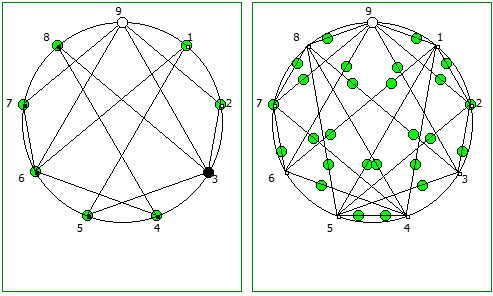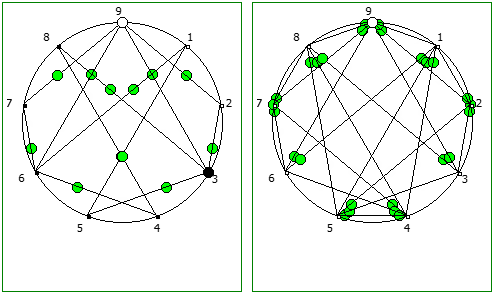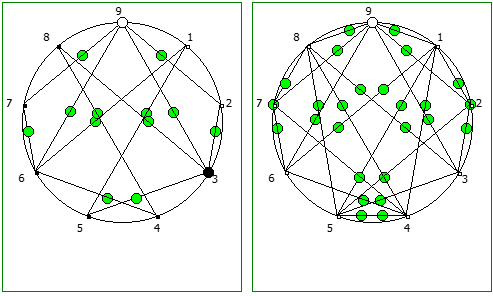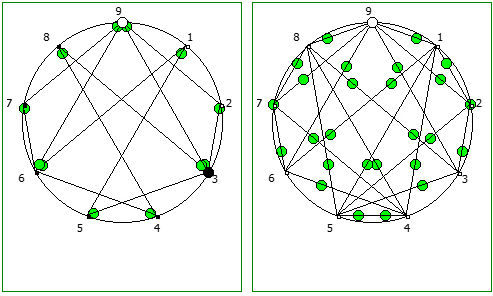
Ещё интересные визуализации, полученные данным методом:
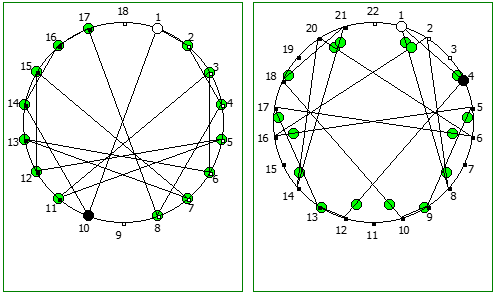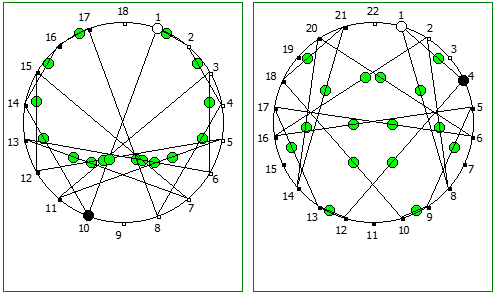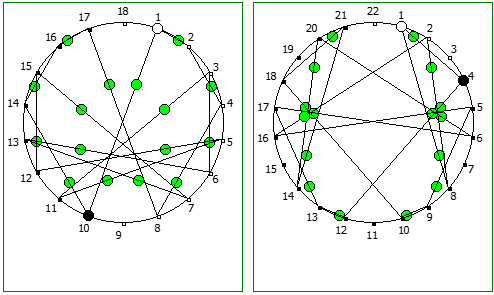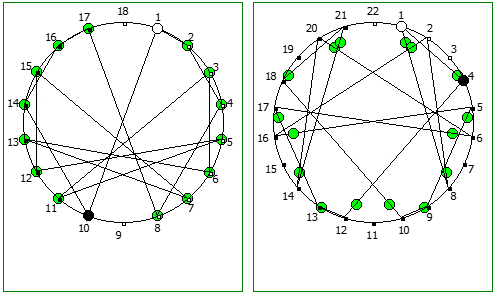
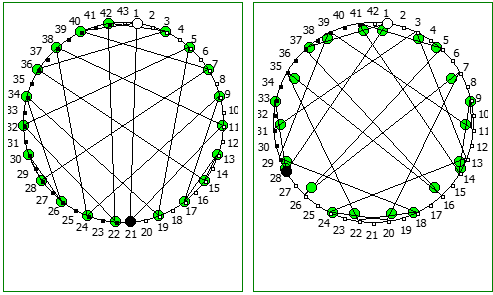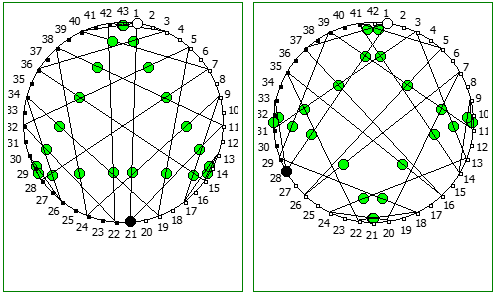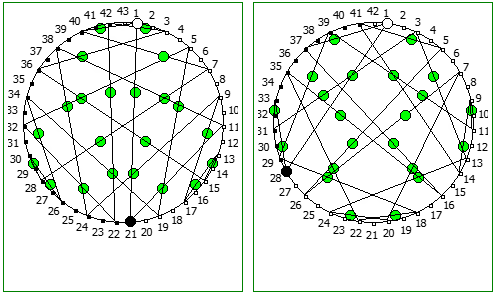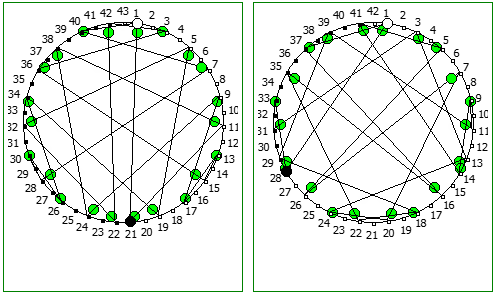
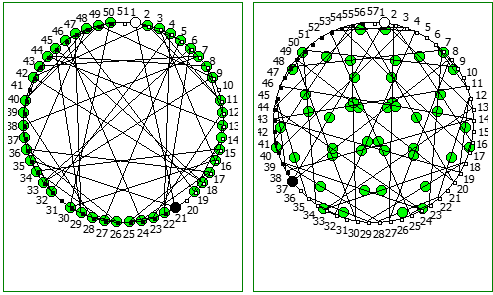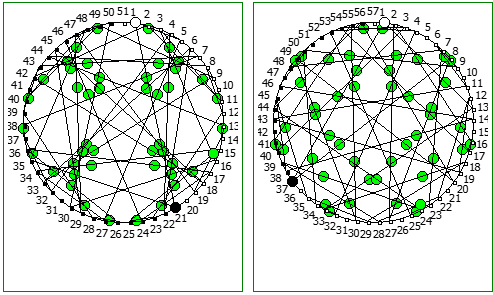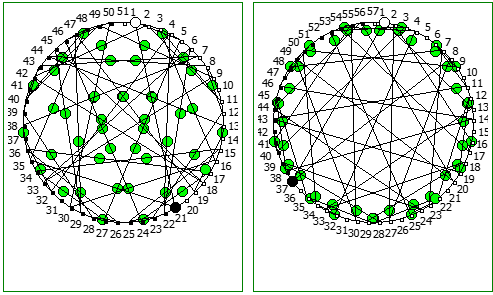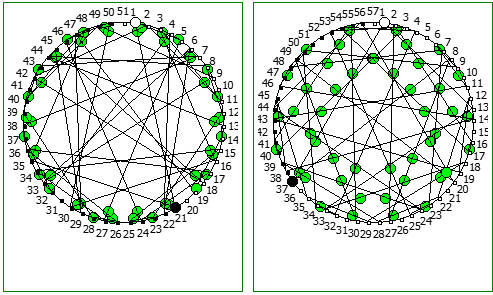
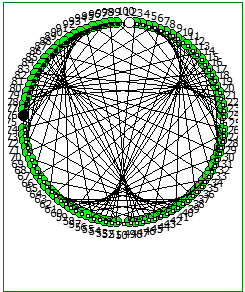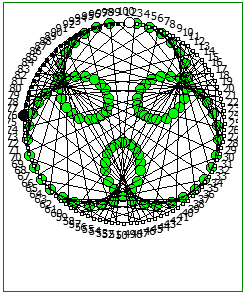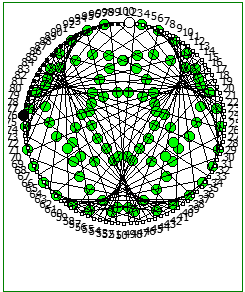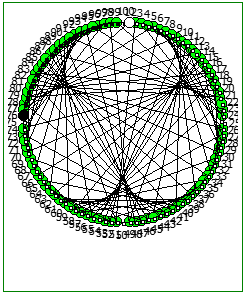
Использование степеней простых чисел в знаменателе тоже дают визуально интересный результат:
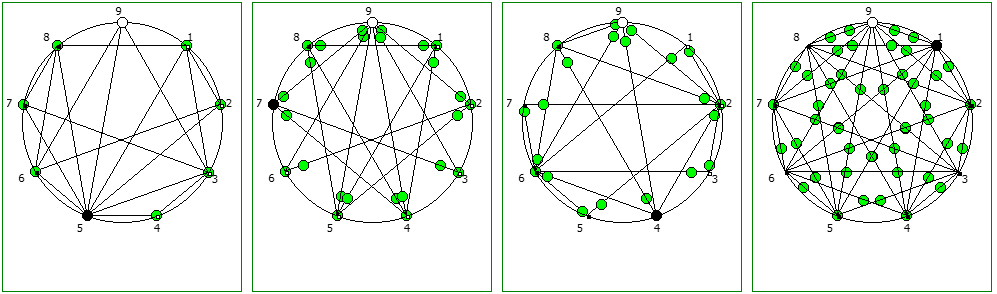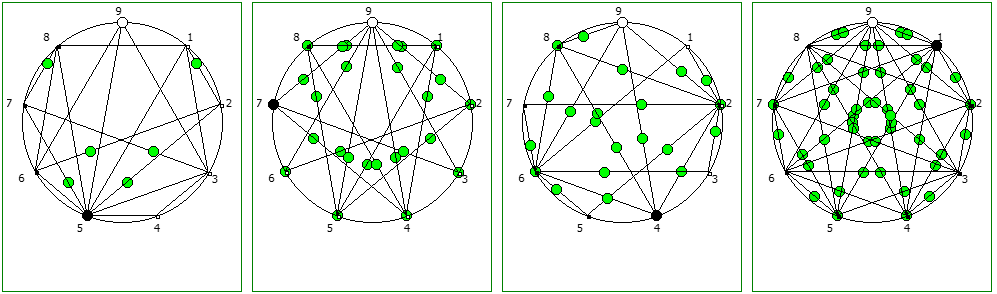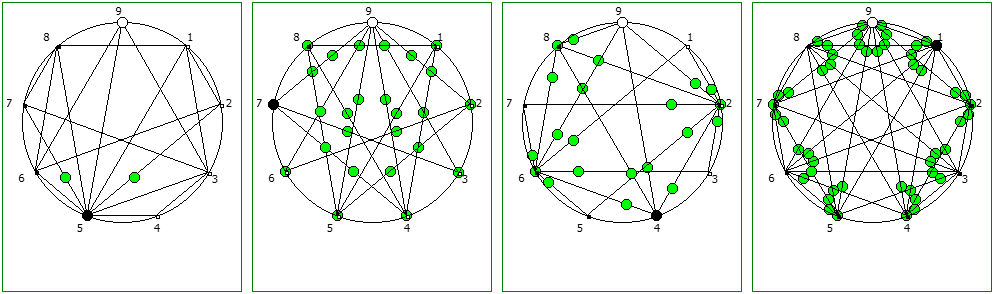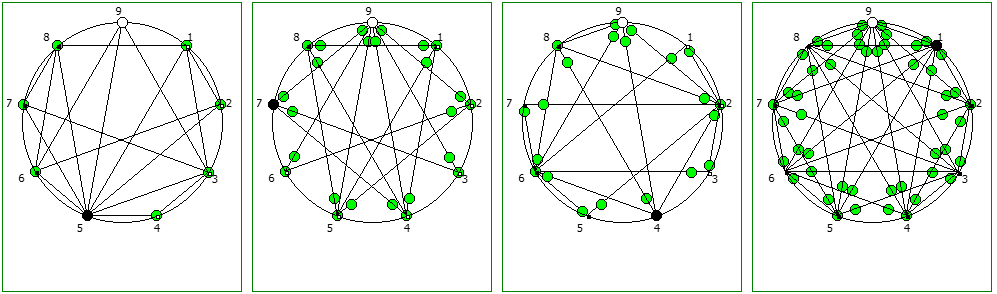
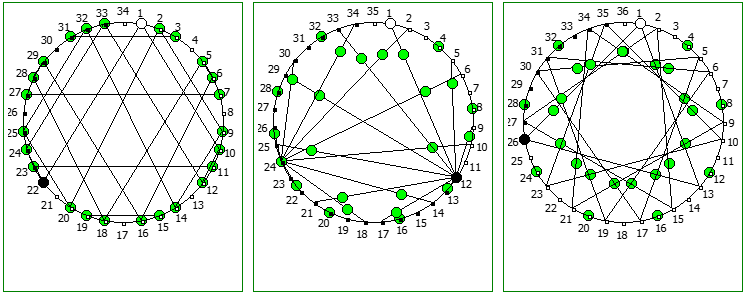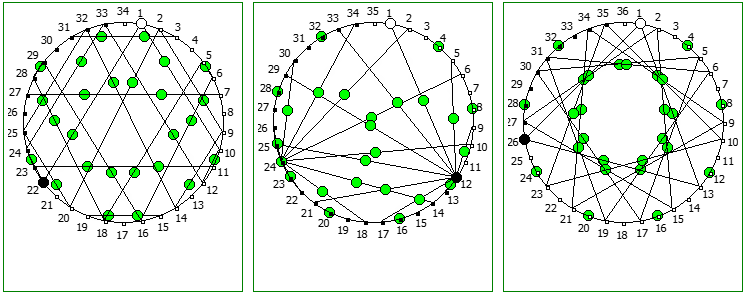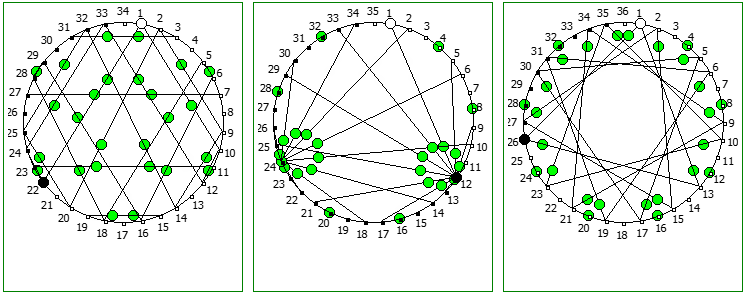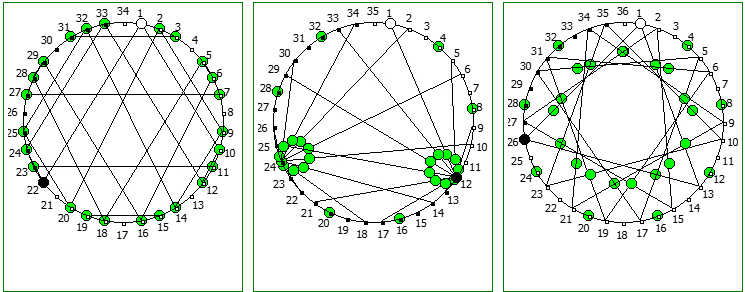
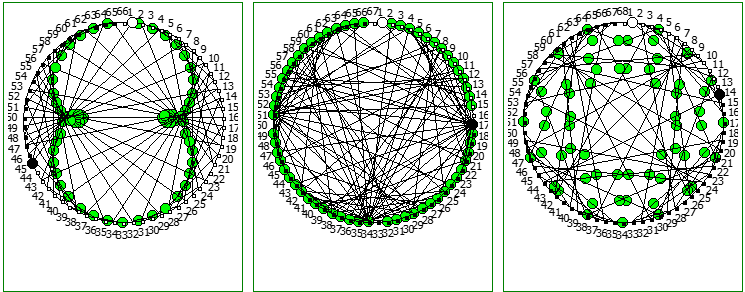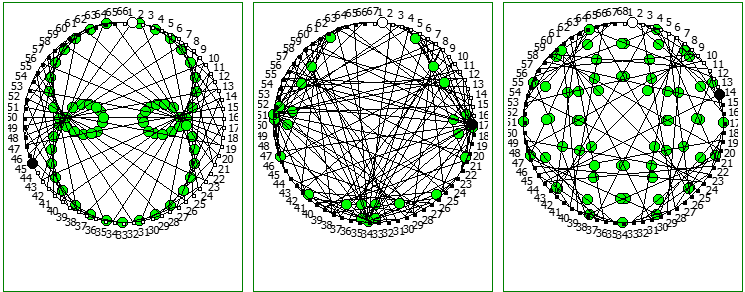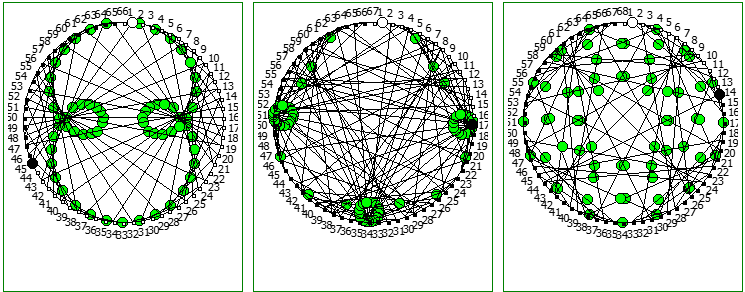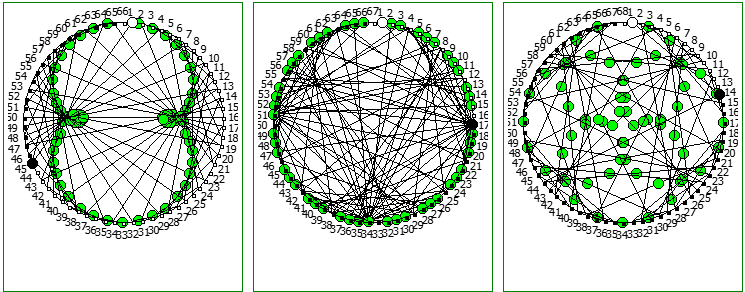
При этом чем больше знаменатель, тем больше «круговых» паттернов образуется при визуализации на системах счисления меньше чем знаменатель:
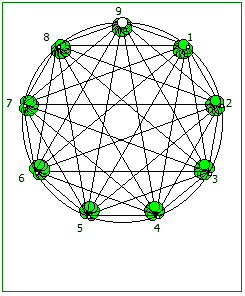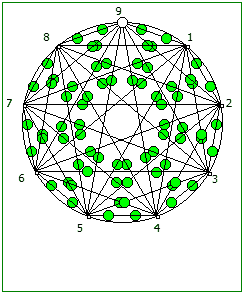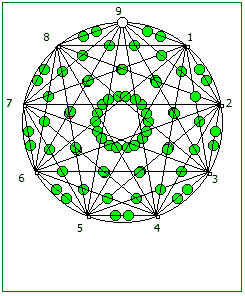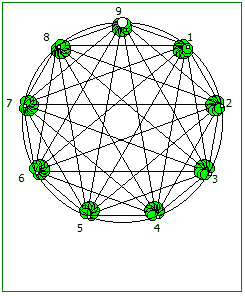
И последний используемый мной метод визуализации структур периодических дробей, это анимация «вращением» дроби. Суть метода проста: для числа 142857 мы делаем поворот по часовой стрелке, и получаем 253968. Далее операция повторяется, пока мы не вернемся к исходному числу — и при визуализации используются все результаты «вращения».
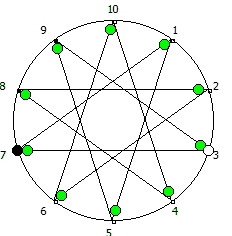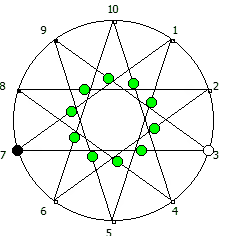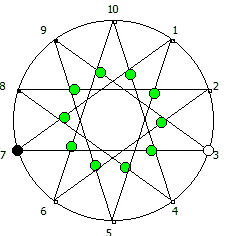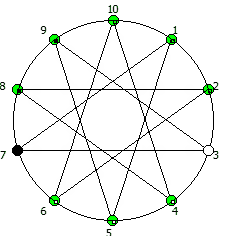
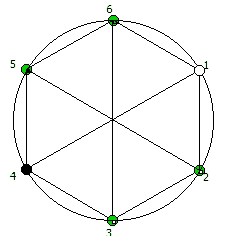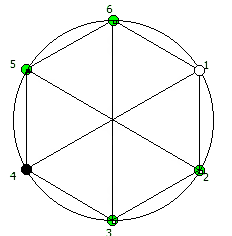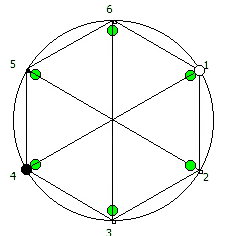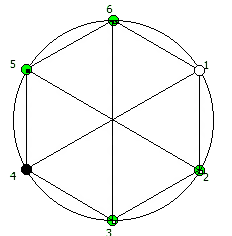
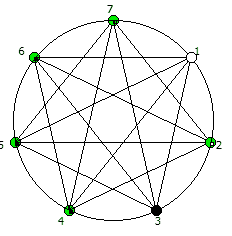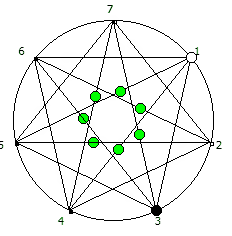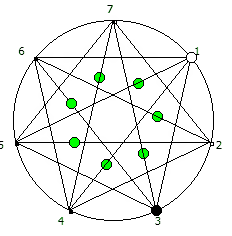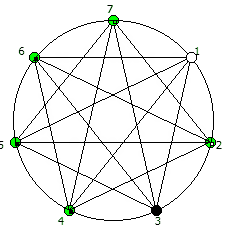
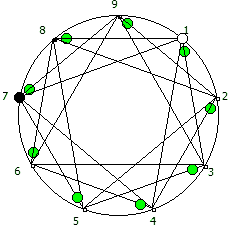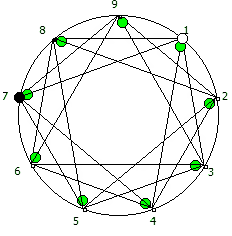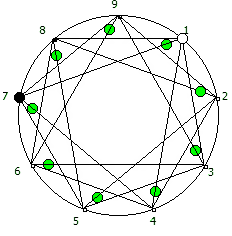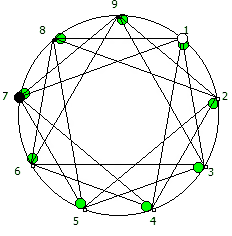
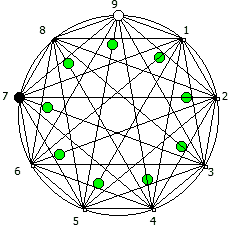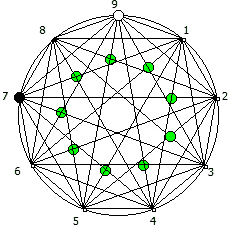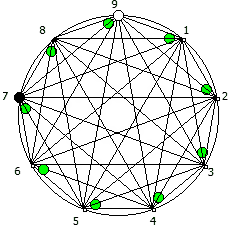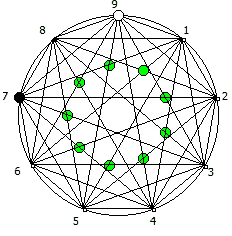
Чем больше простое число, тем больше «орбит» на которых происходит вращение:

Заключение
Визуализация и сонификация были сделаны при помощи приложения разработанного специально для цели написания данной и предшествующей статьи.
Спасибо большое всем за уделённое внимание! .
Мне важно ваше мнение
Наша команда разрабатывает приложение для анализа психоэмоционального состояния человека по голосу, нам очень важно ваше мнение. Мы будем благодарны, если вы пройдёте анкету из 10 вопросов.
Для тех кто запишется на пред-регистрацию мы обещаем скромный, но пожизненный бонус! 🙂


