В этой заметке мы поговорим о том, что такое молекулярная динамика, и как её результаты можно реализовать в виде облаков распределений атомов.
Что такое молекулярная динамика?
Молекулы. Они везде. Они вокруг нас, они в нас, они — это мы. Поэтому если мы хотим понять что-то об окружающем нас мире, например, откуда появляется кислород, которым мы дышим, как что происходит с тефлоном на сковородках, на которых мы жарим утреннюю яичницу, или как работают наши лекарства, нам нужно исследовать динамику молекулярных систем.
Молекул состоят из атомов, а атомы состоят из положительных ядер и отрицательных электронов. Поскольку ядра в тысячи раз тяжелее, чем электроны, вместо задачи о всём этом супе квантовых частиц, мы можем решать две взаимосвязанных задачи: о движении электронов в поле недвижемых ядер, и о движении ядер в усреднённом потенциале от движущихся электронов. Такое разбиение нашей задачи на две: быструю и медленную, называется приближением Борна-Оппенгеймера.
В случае с маленькими и лёгкими электронами, нам всегда приходится обращаться к квантовой механике. Раздел, который их изучает — это квантовая химия. За почти век существования этой дисциплины, у нас накопилось куча методов, позволяющих описывать результаты движения электронов с разной степенью точности/вычислительной стоимости. Для малых систем (до сотен атомов) мы можем использовать очень точные (но дорогие) методы решения уравнения Шрёдингера, получая результаты, даже превосходящие эксперимент по степени точности. Для среднего размера молекулярных систем (до тысяч атомов) точные методы становятся уже вычислительно-неподъёмными. Поэтому мы можем заменить самые дорогие места расчёта какими-то упрощёнными параметризованными моделями, и вуаля: вот у нас теперь есть полуэмпирические методы расчёта, которые имея чуть меньшую точность, могут описывать уже гораздо большие системы. Ну а для систем вплоть до миллиардов атомов, даже упрощённые квантовые модели не помогут. Поэтому на решение задачи об электронах забивают, заменяя их влияние на ядра в виде каких-то параметризованных потенциалов. Стандартный подход — это молекулярная механика, но сейчас всё большую роль начинают играть роль те же нейронные сети.
О молекулярной механике
|Молекулярная механика (на нынешнем этапе развития науки) — это всего-лишь аппроксимация результатов сложных квантовых движений электронов в молекулах (энергий связей, энергий изгиба молекул, дальних взаимодействий, например электростатических или дисперсионных сил) простыми модельными выражениями из школьной физики. Например, растяжение химической связи мы можем представить себе как растяжение пружинки, а взаимодействие двух ионов — как взаимодействие двух зарядов. Из-за этого часто можно встретить чушь, что типа «молекулярная механика — это описание молекул через призму классической физики». Даже в Википедии можно найти такое:
Molecular mechanics uses classical mechanics to model molecular systems.
Это бред. Несмотря на простоту и кажущуюся классичность выражений, никакой настоящей классической механики за этими молекулярными силами не стоит. Молекулярная механика — это всего лишь описание сложных и квантовых вещей простыми выражениями. Ну и тем более молекулярная механика — это не молекулярная динамика. Когда-то давно они были единым целым, но уже давно это не так.
Ядерные движения, в отличие от электронных движений, сложные. Потенциал, в котором движутся электроны, очень простой — это просто кулоновское взаимодействие положительных (ядра) и отрицательных (электроны) зарядов. Поэтому у нас есть более-менее универсальные методы решения задачи о движении электронов. В случае же ядер, потенциал в котором они движутся, получается из движений, и всё, что мы можем о нём сказать, это что он существует. А ядерные движения нам очень нужны. Те самые фононы, за счёт которых распространяется звук в твёрдых телах — это колебания ядер, химические превращения молекул — это тоже перемещение ядер с одного места на другое, или какое-нибудь изменение конформации белка от взаимодействия с каким-нибудь лекарством, блокирующее его биологическую функцию, всё это движения ядер.
И получается, что, нам нужно решить задачу о движении кучи квантовых частиц (ядер) в произвольном потенциале. У нас есть методы, которыми мы можем воспользоваться (см. например, тут), но всё опять упирается в размер нашей молекулярной системы. Если мы захотим взять какой-нибудь небольшой белочек на пару тысяч атомов, наши квантовые методы описания движений ядер накроются медным тазом.
И тут нам на помощь приходит понятие длины волны де Бройля. Она имеет вид
Где λ — это та самая длина волны, h=6.626×10-34 Дж·с — это константа Планка, m — масса частицы, а v — её скорость.
Эта величина по-сути показывает масштаб, на котором проявляются всякие забавные квантовые свойства для заданной частицы: интерференция, туннелирование и прочее. Если λ заметно меньше масштаба, на которых движется частица, то квантовыми эффектами можно вполне пренебречь. Скорость движения частиц у нас может быть связана с температурой системы формулами из молекулярной физики:
где kB=1.38×10-23 Дж/К — жто постоянная Больцмана, а T — температура системы. Подставив это выражение в длину волны де Бройля, мы получим т.н. термическую длину волны де Бройля:
В итоге, если мы возьмём, например, атом железа (Fe) с массой m=56 а.е.м. = 9×10-26 кг, то при комнатной температуре (T=25oC≈300 K) мы получим термическую дебройлевскую длину волны
Здесь мы воспользовались единицей под названием ангстрем, 1[Å] = 10-10[м]. Длины химических связей имеют размеры порядка единиц ангстремов, поэтому получается, что уже при комнатных температурах, мы можем описывать движение ядер в процессах разрыва/образования химических связей, не прибегая к квантовой механике, только используя классическую физику.
Т.е. нам достаточно задать начальные координаты/скорости каждого из ядер, а дальше брать второй закон Ньютона, и интегрировать эти уравнения движения, получая всякие траектории. Потенциал, а значит и силы, действующие на ядра, у нас будут создаваться электронами, поэтому мы можем использовать или квантово-химические методы (если наша система не очень большая), или молекулярную механику (для больших систем). И вот этот метод классического моделирования движения ядер в молекулах и называется молекулярной динамикой. Этот метод просто замечательный, с помощью него мы можем описывать вообще-вообще всё, что мы хотим: от фотохимии маленьких молекул, до потенциальных мишеней для борьбы с вирусом ковида.
Пару слов о начальных условиях. Начальные координаты, очевидно соответствуют пространственному расположению атомов в нашей системе, поэтому их положение по-сути определяется нашим собственным интересом (какие именно молекулы мы изучаем). А вот скорости мы можем задавать, например, из распределения Больцмана. Т.е. считать, что каждая конкретная компонента скорости ядра с массой m задана гауссовым распределением
где p0 — это некая постоянная.
Что мы хотим получить?
Вот представим, прогнали мы себе молекулярную динамику. У нас получилось по-сути кино о движении молекулы: куча последовательных кадров, на которых нашу молекулярную систему колбасит. И вот мы хотим сделать какой-то вывод о том, что происходит. Мы можем, конечно, записать разбор в стиле BadComedian для того треша, что мы получили, разобрать каждый момент, и понять что-то о Жизни, Вселенной и вообще. Но вместо траты кучи времени на просмотр, было бы неплохо может глянуть на некую статичную картинку, из которой нам бы стало всё понятно.
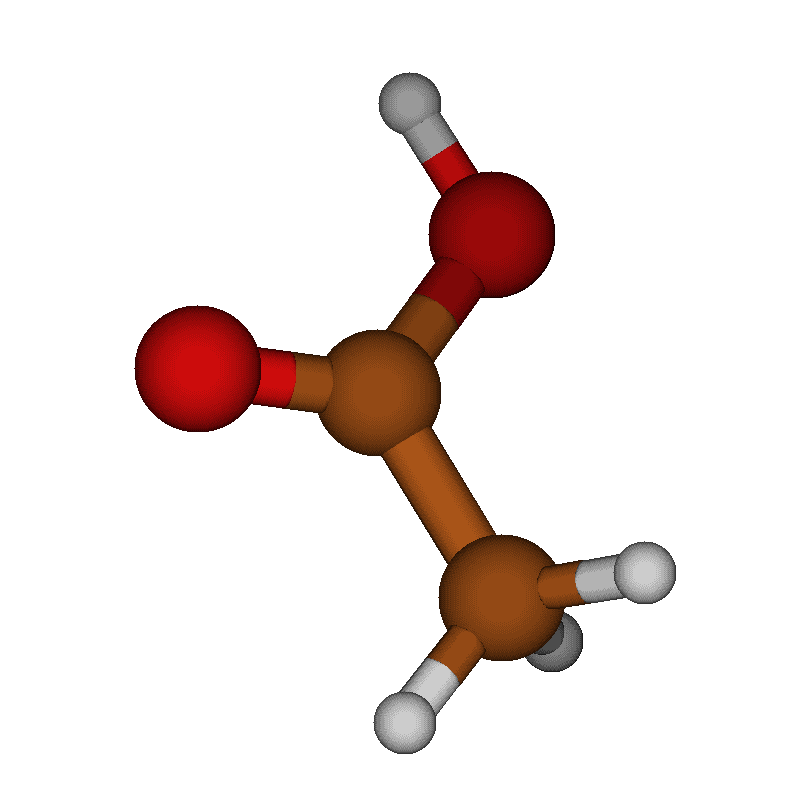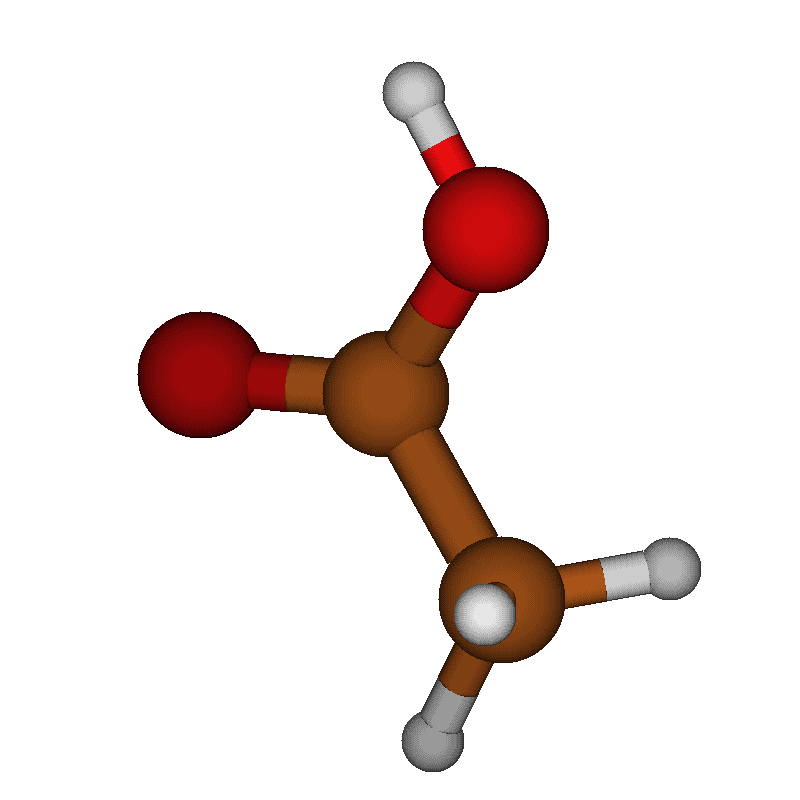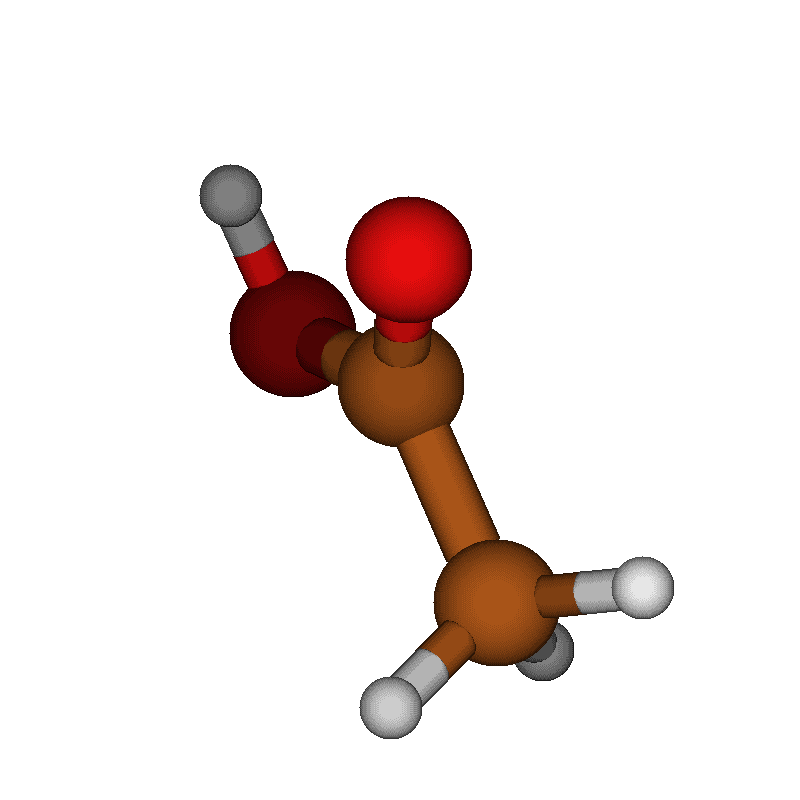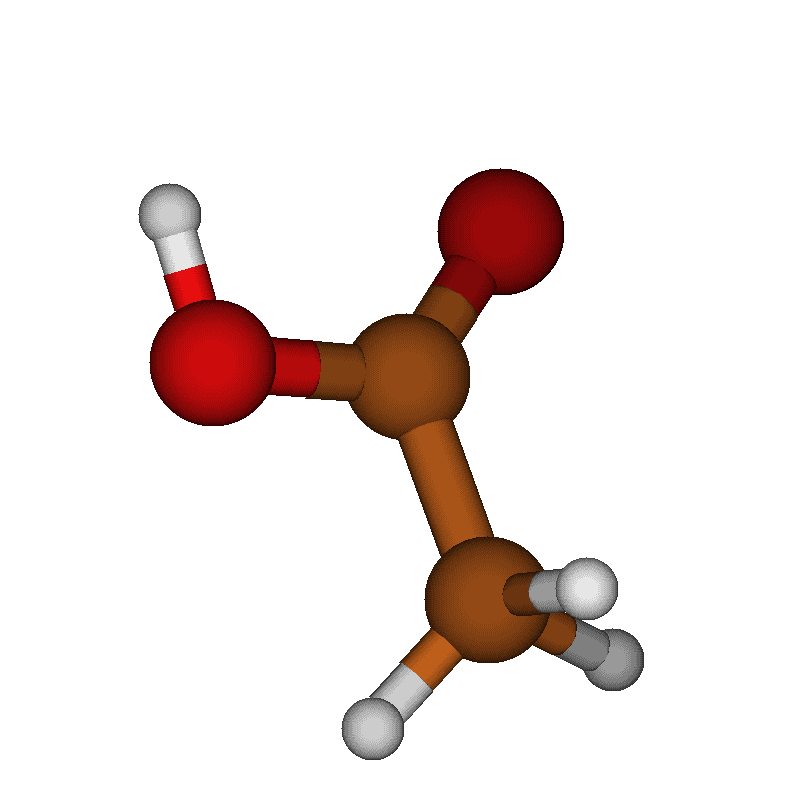
Возьмём для примера молекулярно-динамическую траекторию уксусной кислоты (CH3COOH), приведённую в начале статьи. Мы можем отрисовать все кадры одновременно, и получить нечто неудобоворимое:
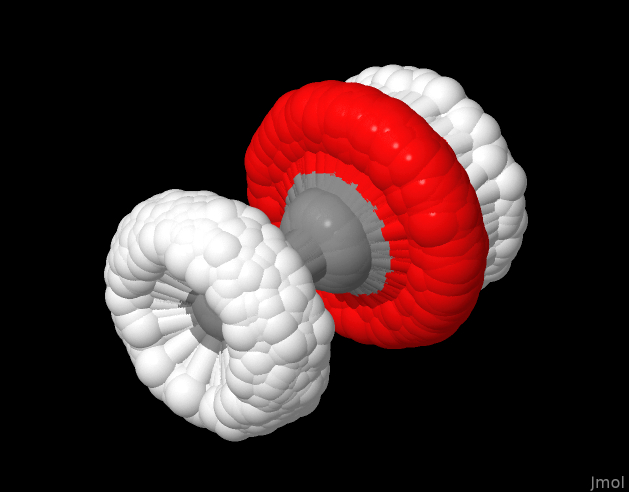
Вроде понятно, что что-то крутится относительно другого, но ничего более внятного сказать нельзя. А если бы мы изначально как-то совместили все кадры по-умному, мы смогли бы отрисовать не сами позиции каждого атома, а их распределение в пространстве. В результате чего из получившейся картинки мы бы сразу поняли, что вращается не всё, а только метильная группа (CH3), относительно карборксильной группы COOH, вокруг связи C-C.
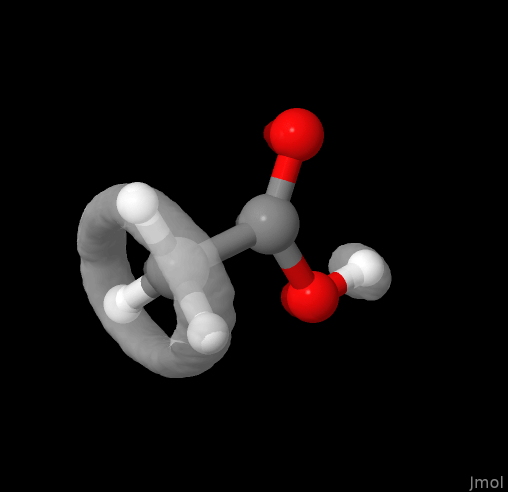
Данные для таких изображений умеет делать программа TRAVIS. Вот, например, результат её творчества:

Относится этот немецкий код к замечательному классу программ «всё на свете и топор». Сложно найти, что эта программа не может сделать с результатами молекулярно-динамического моделирования. Но для этого придётся пройти сто кругов ада, нудное общение в терминале с программой в стиле текстовых квестов 80-х, и последующее визуализирование результатов расчётов. Поэтому, я решил написать свой говнокод на Питоне, позволяющий даже такому недалёкому недотёпе, как я, рисовать такие картинки.
Нужно нам сделать следующие стадии:
-
получить где-то молекулярно-динамические траектории,
-
прочитать их и как-то обработать,
-
получить распределения и сохранить их в каком-то удобочитаемом виде,
-
нарисовать получившийся результат в какой-то внешней программе.
Пишем код
Для начала нам бы неплохо было получить кучу стандартных табличных данных в том виде, в котором мы легко можем их использовать в нашем коде. Для этого можно было бы воспользоваться модулем Mendeleev, но это как стрелять по воробьям из пушки (он почему-то у меня работает достаточно медленно). Поэтому мы можем выгрузить минимум необходимых нам данных:
-
сопоставить атомный символ (те самые двухбуквенные обозначения, типа H — водород, Fe — железо и т.д.) .
-
зарядом ядра (Z), он же порядковый номер в таблице Менделеева,
-
атомным весом (m), той самой усреднённой массой всех изотопов данного типа элемента, взвешенной по распространённости этих самых изотопов.
На самом деле нам лучше бы подошла масса самого распространённого/стабильного изотопа вместо атомных весов, но разница будет не сильной, так что нечего заморачиваться. Данные сохраним в виде словаря, где кейвордами будут одно/двухбуквенные обозначения элементов, а значение словаря будут другие словари с теми самыми тремя свойствами, что мы описали выше. Выгрузить это можно кодом, убранным под спойлер.
код для выгрузки данных из Mendeleev
#! /usr/bin/python3
import mendeleev as m
# вот сюды, в этот текстовый файл мы и сохраним наше драгоценное сокровище атомных данных
outf=open("element_properties.stolen", "w")
# начинаем писать всякую фигню
outf.write("# Data stolen from mendeleev module on "+str(date.today())+"\n\n\n")
outf.write("ElementData = {\n")
Zmax = 118 # это максимальный атомный номер, что мы возьмём
# собственно, выгружаем всё + пишем в удобочитаемом виде
for i in range(1,Zmax+1):
try:
try:
El = m.element(i)
name = El.name
elRef = str(El.symbol).lower()
elSymb = El.symbol # element symbol
jmolCol = El.jmol_color
Z = i # this is the atomic charge
weight = El.mass
dCont=""atZ": "+str(i)+", "
dCont += '"atSymbol": "'+elSymb+'", '
dCont += '"color": "'+str(jmolCol)+'", '
dCont += '"atWeight": '+str(weight)+" "
outf.write('"'+elRef+'": {'+dCont+"}")
if not i == Zmax:
outf.write(",")
outf.write("\n")
except:
outf.close()
raise RuntimeError("Extraction failed at the Z=%i" % (i))
outf.write("}\n")
outf.close() # не забываем закрыть файл с записанным :)Молекулярно-динамические траектории обычно все возможные программы для молекулярного моделирования сохраняют в формате XYZ. Он не очень стандартизован, поэтому и тут и там можно найти его модификации, допиленные для конкретных целей. Но ядро его более-менее простое и стабильное. Он состоит из повторяющихся блоков, блоки идут сплошняком. Первая строка блока содержит только одно единственное целое число: число атомов в нашей молекулярной системе. Вторая строка блока — это строка комментариев, туда можно записать что угодно. А далее идут строки вида , где первый символ в строке () — это обозначение символа элемента, а дальше идут три декартовы координаты (
-
открыть файл,
-
прочитать первую строку, выгрузить следующие строки с координатами, их обработать, сохранить в удобоваримом виде, используя данные, ранее выгруженные из Mendeleev,
-
во время обработки убрать центр масс, чтобы все фреймы имели один и тот же центр,
-
повторить действие с блоками, пока не будет возникать ошибки на какой-то стадии обработки.
-
а потом закончить и вернуть траекторию как набор фреймов.
В нашем самопале это сделано двумя функциями: LoadTrajectory, читающей весь файл, и вспомогательной LoadSingleStructure, обрабатывающей один блок траектории, убранными под спойлер.
Чтение молекулярно-динамической траектории
# this function loads a single structure from the XYZ trajectory file
def LoadSingleStructure(inpf):
try: # if we can read the XYZ structure, everything is good
FirstLine = inpf.readline()
NumOfAtoms = int(FirstLine) # the first line should contain only the numbers of atoms
inpf.readline() # skip empty line
# read NumOfAtoms of next lines, split the words in line, store the results as an NumPy array
StructLines = np.array([inpf.readline().split() for n in range(0,NumOfAtoms)], dtype = str)
#print(StructLines)
AtSymbLower = np.array([a.lower() for a in StructLines[:,0]]) # these are elements notations, in lowercase
#print(AtSymbLower)
AtSymbNorm = np.array([ElementData[a]["atSymbol"] for a in AtSymbLower]) # these are normal elements notations
#print(AtSymbNorm)
AtMass = np.array([ElementData[a]["atWeight"] for a in AtSymbLower]) #
#print(AtMass)
XYZ = np.array(StructLines[:,1:4], dtype=float) # these are XYZ coordinates
#print(XYZ)
# remove center of mass at the stage of trajectory loading
RCM = np.zeros(3)
for i in range(0,len(AtMass)):
RCM += XYZ[i] * AtMass[i]
RCM /= np.sum(AtMass) # these are now the coordinates of the center of mass
for i in range(0,len(AtMass)):
XYZ[i] -= RCM
return AtMass, AtSymbNorm, XYZ
except: # if not, we just don't return anything, and this will stop the processing later
return None
# load the trajectory from the file with name "FileName" (str)
# return: List of atomic weights, List of atomic symbols, List of XYZ coordinates for each MD frame
def LoadTrajectory(FileName):
try:
inpf = open(FileName, "r") # open the MD trajectory file
AtMass = []
AtSymb = []
MDTrj = []
Check = True
while Check:
res = LoadSingleStructure(inpf)
if res is None:
Check = False
else:
AtMass.append(res[0])
AtSymb.append(res[1])
MDTrj.append(res[2])
inpf.close() # close the MD trajectory file
print("Loaded trajectory from file %s with %i frames " % (FileName, len(MDTrj)))
return AtMass,AtSymb,MDTrj
except:
raise RuntimeError("Failed to load trajectory from file "+str(FileName))Далее, полученную траекторию нужно ориентировать (повернуть) относительно некой референсной структуры, чтобы все структуры были сопоставлены друг с другом. Это может быть просто первый фрейм в траектории, или же некий XYZ-файл данный юзером (его читаем точно так же). Чтобы ориентировать структуры мы можем использовать алгоритм Кабша, который очень удобно реализован в SciPy. Обёртку для него мы уберём в отдельную функцию, OrientStructureWRTRef.
OrientStructureWRTRef
import scipy.spatial.transform as spst
# orient the structure with respect to the reference structure
# requires: masses M, XYZ (coordinates to be oriented), and
# RefXYZ (coordinates of the reference structure)
def OrientStructureWRTRef(M, XYZ, RefXYZ):
# this is the Kabsh algorithm application
Res = spst.Rotation.align_vectors(RefXYZ, XYZ, weights = M)
Rot = Res[0] # this is the rotation to orient
RotMat = Rot.as_matrix() # get rotation matrix
RotAng = Rot.as_euler('zxy', degrees=True) # get the Euler angles of rotation (just in case)
newxyz = np.array([np.matmul(RotMat,r) for r in XYZ]) # and get the newly rotated structure
return newxyzПосле всех этих мучений, мы можем начинать считать распределения атомов в пространстве. Для этого мы определяем виды различных атомов, которые у нас имеются, чтобы хранить их распределения по-отдельности. Самым простым (хоть и оооочень неэффективным) форматом хранения распределений в 3D пространстве, который читают почти все молекулярные визуализаторы, является гауссиановский формат cube. Плотность в нём хранится на сетке, задающей трёхмерный куб с Nx, Ny, Nz точками по координатам x, y, z, соответственно. Нам всего-то нужно задать стартовую точку этого кубика, шаг по каждой из координат, да плотности в каждой из точек, заданные через три вложенных цикла для каждой из сторон. Так это мы и сделали. Ну и напоследок, чтобы не мучиться с разными визуализаторами, я добавил фичу для того, чтобы сгенерировать скрипт, строящий картинку в моём любимом визуализаторе, Jmol.
Для того, чтобы взаимодействовать с юзером, был прикручен command line interface с помощью питоновского модуля Argparse. Юзеру были добавлены следующие опции.
-
-t TRJ, --trj TRJ— собственно имя того XYZ файла с траекторией, который мы хотим обработать. -
-r REF, --ref REF— а это опциональное имя другого XYZ файла, содержащего какую-то другую референсную геометрию. -
--smooth— это флаг для того, чтобы сгладить наше распределение трёхмерным гауссовым фильтром из SciPy.ndimage. Этот параметр связан с другим, -
--sigma SIGMA— это собственно ширина того гауссова фильтра. -
--nx NX, --ny NY, --nz NZ— это размер нашего кубика, -
--offx OFFX, --offz OFFY, --offz OFFZ— это оффсет для размера куба по каждой из координат, -
--savetrj— флаг, чтобы сохранить ориентированную траекторию (вдруг захочется картинку построить), -
--jmol— а этот флаг заставляет прогу выкинуть скрипт для Jmol, для него есть ещё один параметр -
--cutoff CUTOFF. Этот параметр отсечку для изоповерхности, которую строит из куба Jmol.
Про последний параметр скажу пару слов. Собственно, формат cube был разработан компанией Gaussian Inc. для построения орбиталей. Орбитали — это те же трёхмерные пространственные распределения. И многие ошибочно полагают, что картинки во всяких учебниках — это почти всегда какой-то квантиль этого трёхмерного распределения, но это слишком гемморойно. Поэтому на практике обычно рисуют изоповерхности распределения: т.е. такую поверхность, где распределение p(x,y,z) равно некой заданной постоянной. Вот эту величину и называют величиной отсечки. Очевидно, чем больше эта величина, тем более компактную часть распределения мы будем видеть, а чем больше, тем больше хвостов распределения мы будем наблюдать, поэтому наблюдаемое распределение будет большим. Это можно наблюдать невооружённым глазом, в частности, на примере той же самой динамики уксусной кислоты.
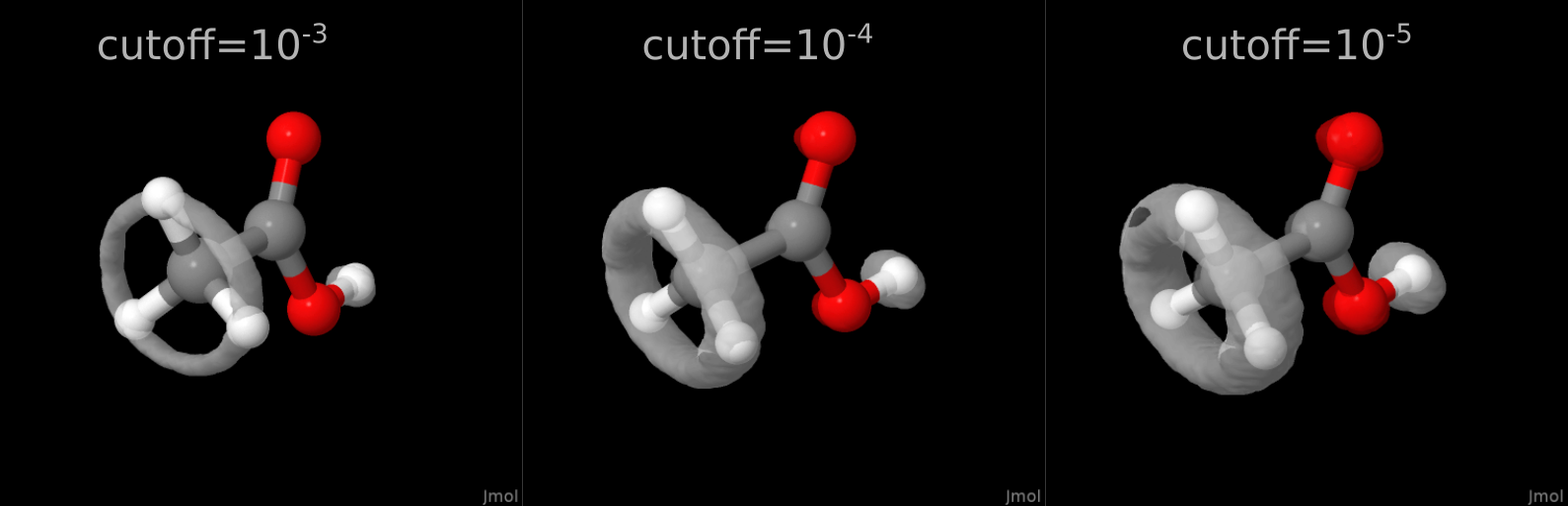
Полный код доступен в моём репозитории CubeTheMD на Gitlab.
Что мы теперь можем делать?
Мы теперь можем строить такие вот карты распределений, которые занимают атомы во время колебаний молекул. Сразу отметим, что наш код не предназначен для по-настоящему больших молекулярных систем, там у них своих методов визуализации полно, и они абсолютно другие. Наш метод подходит для систем до пары сотен атомов, то, для чего мы можем прогнать молекулярную динамику с полновесной или полуэмпирической квантовой химией.
Чтобы продемонстрировать возможности современной молекулярной динамики, воспользуемся пакетом полуэмпирической квантовой химии XTB, от группы очень известного теоретического химика, Штефана Гримме из Бонна. Скачать эту программу с Github может каждый. Если у нас есть XYZ файл с начальной геометрией нашей системы (допустим, ini.xyz), мы можем запустить молекулярную динамику при комнатной температуре простой командой в командной строке: xtb ini.xyz --md. И всё, пикосекундную траекторию для небольшой молекулы мы можем получить на обычном ноутбуке где-то за минуту.
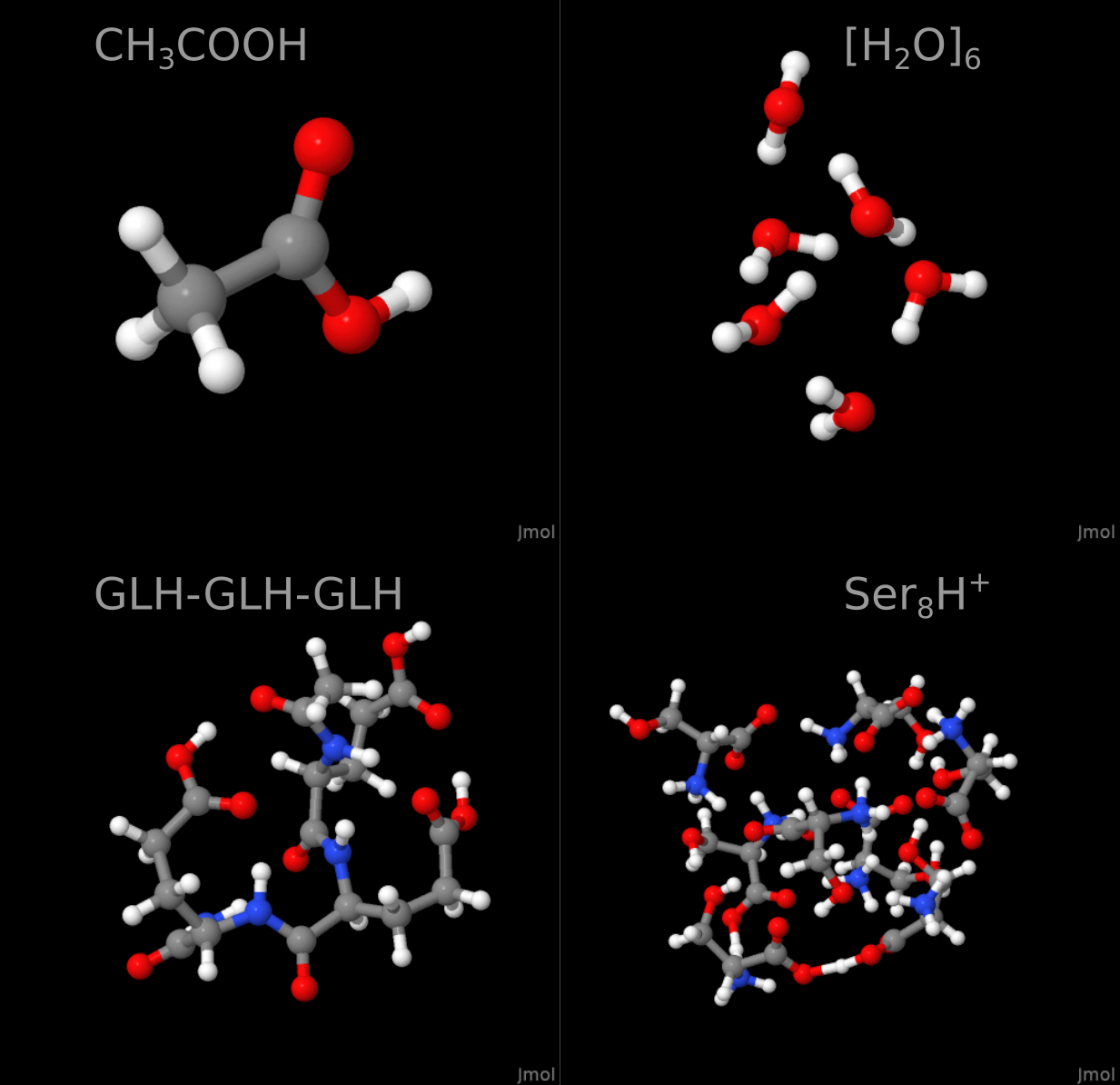
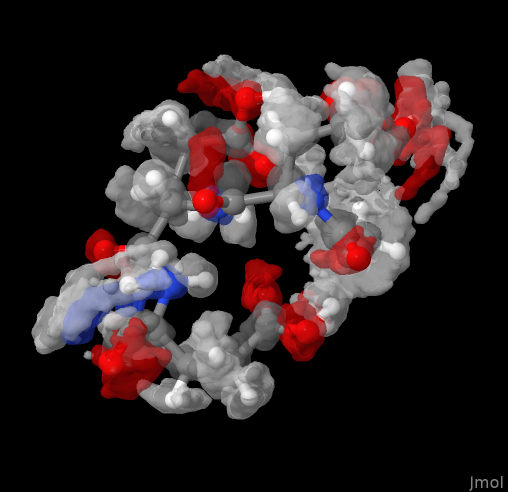
Чтобы продемонстрировать возможности, я взял несколько примеров разных небольших молекулярных систем (см. рис. выше).
-
Собственно, уксусная кислота (CH3COOH), картинки и видео с которой мы уже видели по ходу изложения.
-
Гексамер воды ([H2O]6). Кластеры воды образуются везде и всегда, поскольку за счёт сетки водородных связей они очень стабильны. Кластеры воды — это одни из тех молекулярных структур, которые отвечают за голубой цвет неба над нашей головой. Начальную структуру гексамера воды я спёр из The Cambridge Cluster Database.
-
Трипептид GLH-GLH-GLH, что бы это ни значило, (C17H26N5O11), начальную структуру которого я спёр из базы данных PEPCONF, размещённой на Github.
-
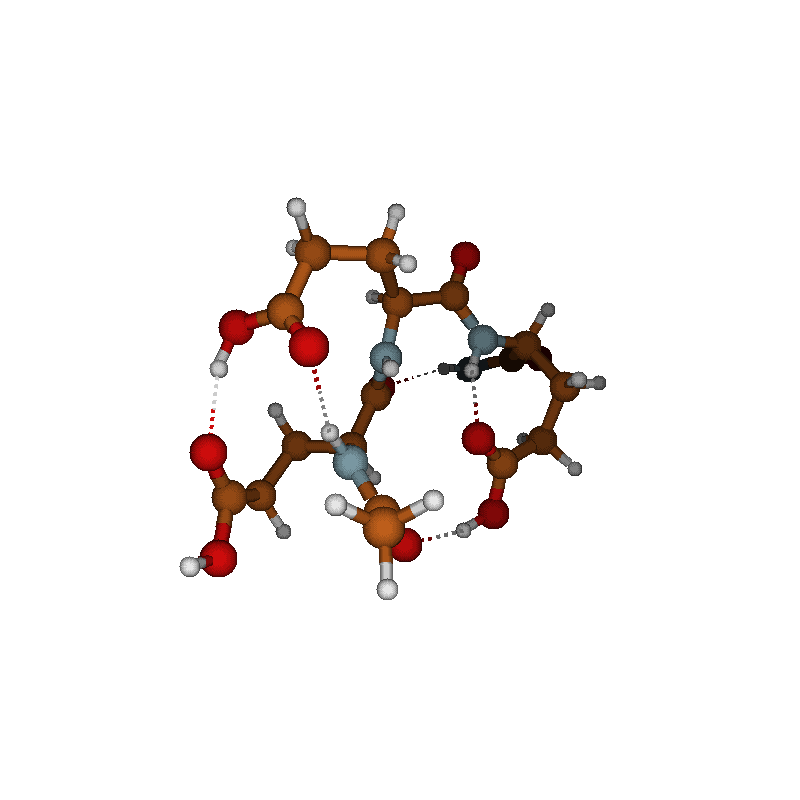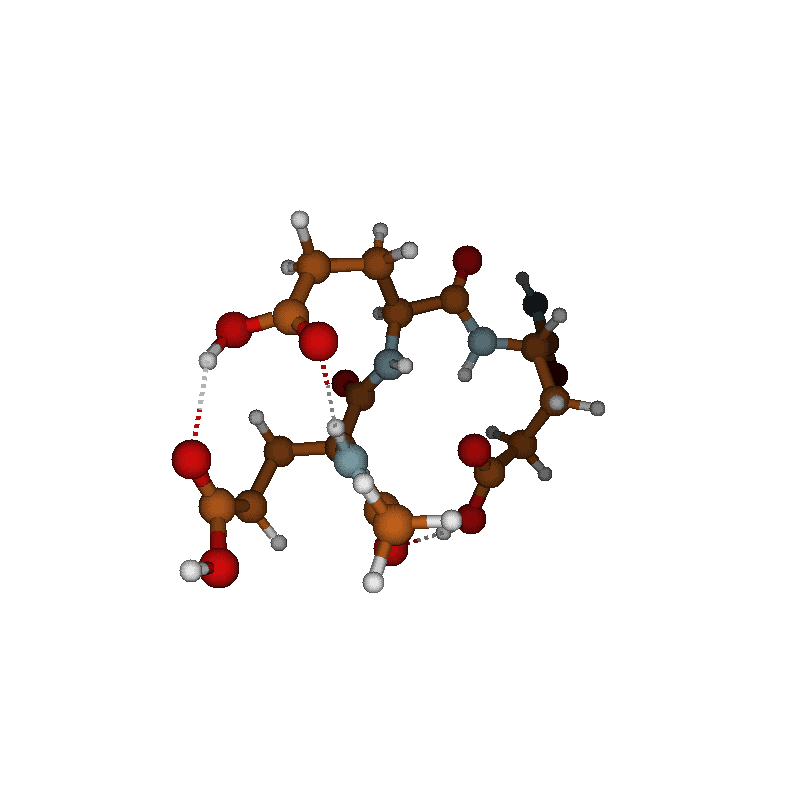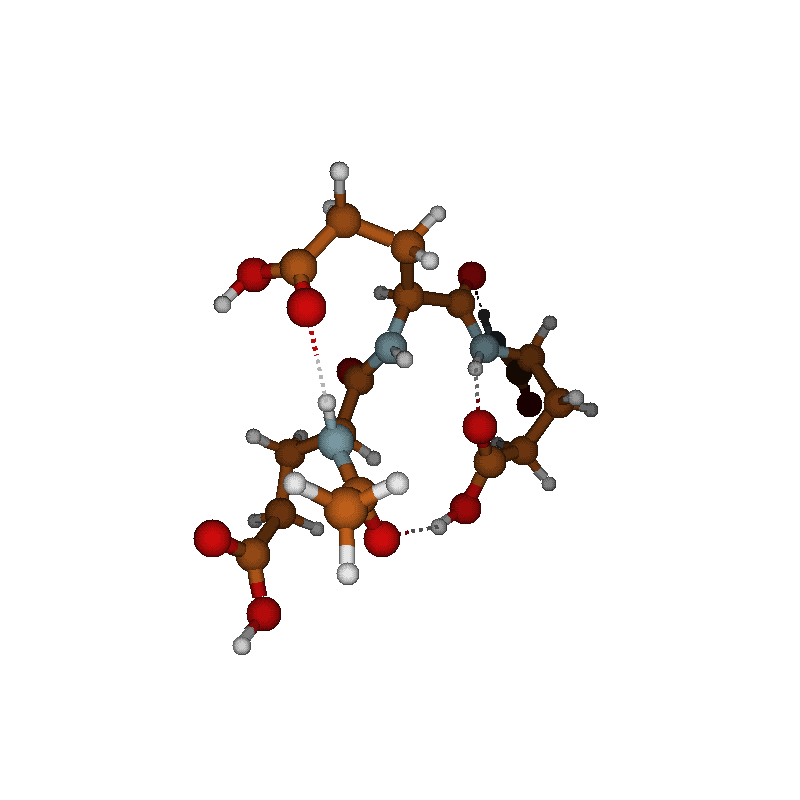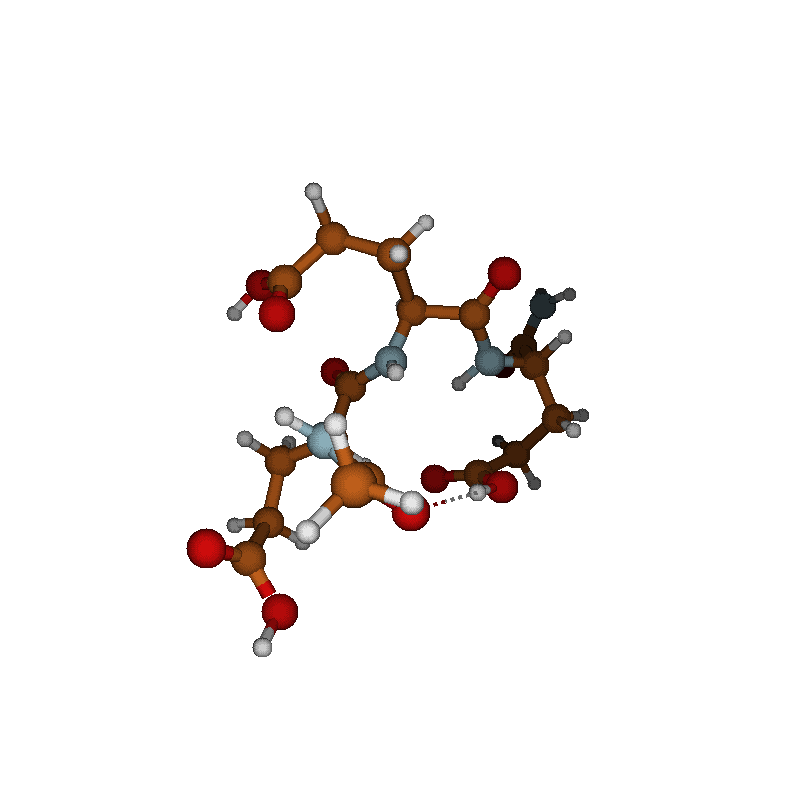
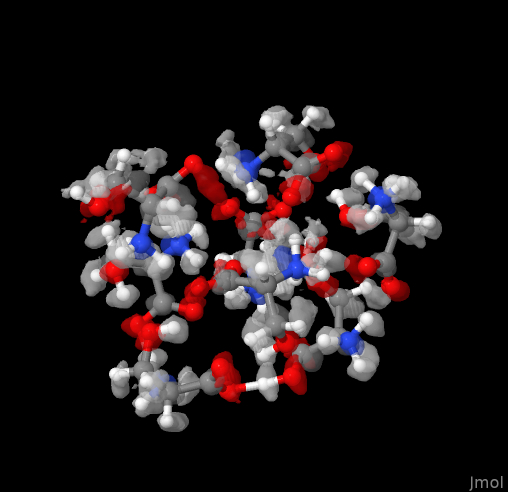
Ну и напоследок я взял достаточно большую систему: протонированный октамер серина, Ser8H+ ([C3H7NO3]8H+). Этот магический кластер считается одним из возможных источников гомохиральности в живых системах. И не так давно его структура была установлена с помощью ИК-спектроскопии с гелиевой меткой (есть даже научпоп изложение этой работы на N+1). Вот из той статьи я начальную структуру и спёр. В этом случае у нас был позитивный заряд на молекуле (из-за протона), поэтому команда запуска молдинамики была немного другой, чтобы это учесть (дефолтный заряд всегда нулевой):
xtb ini.xyz --md --charge 1.
Координаты этих систем тоже тут даны (под спойлером ниже).
XYZ координаты использованных молекулярных систем
Уксусная кислота
8
energy: -14.459941578881 gnorm: 0.000687598507 xtb: 6.4.1 (afa7bdf)
C 0.77137155792730 0.97159927347745 1.00412971650796
C 2.05219955377474 1.75310074172004 0.95239563716272
O 3.04713675532760 1.03389614757515 0.41257538503574
O 2.20660069260610 2.88136834138410 1.33164209116674
H -0.01670542205310 1.58169949266812 1.43351517607217
H 0.49997710070902 0.66040036485924 -0.00179075286421
H 0.92238885933225 0.07746247695181 1.60423688430530
H 3.86541080974369 1.55371569959882 0.38513091903241Гексамер воды
18
energy: -30.496336532314 gnorm: 0.000756370053 xtb: 6.4.1 (afa7bdf)
O -1.98579007830630 0.97744753028137 1.73200537135790
H -1.97657008953497 1.61051906305706 2.44975206160930
H -1.49545907799358 1.39053753019975 0.98797635778567
O -0.58068455321744 -1.29328920501500 1.09678648964405
H -1.19788438840311 -0.63742085724813 1.46841360009974
H 0.30003884000197 -0.89098478934444 1.17277295980267
O 1.81787740126284 0.10961571962522 0.70173001370620
H 1.93873624850369 -0.21402229727634 -0.22090005448358
H 2.65661961127810 -0.01210672807330 1.14731612593756
O -0.84371093376594 -0.85434670123486 -1.47907059193333
H -1.51453812742245 -1.40935568727674 -1.87778321986513
H -0.79923433572306 -1.11686956606482 -0.51577270623421
O -0.33877934886259 1.68065349448684 -0.29426044673575
H -0.61494586638917 0.97965348643537 -0.90240534440724
H 0.47256614307120 1.35431529629239 0.12041210564318
O 1.81870873320761 -0.62548719913040 -1.87876195413248
H 1.92883708750698 0.10615086745315 -2.48897301123984
H 0.85952401836910 -0.82489951124319 -1.86234778713915Трипептид GLH-GLH-GLH
57
energy: -102.175440608807 gnorm: 0.000687330248 xtb: 6.4.1 (afa7bdf)
H -0.82732302190794 3.20499731185248 -3.04936842305220
C -0.11578307547550 4.02198341089050 -2.97685586074532
H -0.26312139640526 4.57679850664812 -2.05447812961370
H -0.28249826243543 4.69986289415282 -3.81298861455173
C 1.30607687467798 3.53517862389170 -3.05823998575478
O 2.24257003533814 4.13292562482019 -2.54490700726174
N 1.46318671925312 2.39045016846417 -3.74709201387230
H 0.64396485518143 1.95583186816873 -4.16004413413932
C 2.75692148690309 1.82212406098693 -4.03436451009170
H 3.50190101023779 2.46126989668543 -3.54781864446309
C 2.88251420315774 0.38744345622200 -3.48680978552599
H 2.29174121016240 -0.29407816795632 -4.10276659437736
H 3.92727882408943 0.08895610934644 -3.56282650127803
C 2.40706952686861 0.29704642618072 -2.03895132513454
H 2.72234041780698 -0.65832137768990 -1.61152155818809
H 2.82355826259964 1.09852636751584 -1.42879305882751
C 0.90617392279542 0.34291258731257 -1.93546502057007
O 0.13239404122896 -0.14787178832764 -2.72753977101702
O 0.49357373069710 0.95706903048528 -0.83510140054402
H -0.47499575679699 0.95185303021639 -0.76264967562256
C 3.07723546005826 1.73028028048110 -5.53211951644570
O 4.18783599854036 1.41475709260913 -5.92182291271310
N 2.03108595831804 1.91028603543845 -6.35064624416619
H 1.21767968093345 2.40462769597139 -6.01469297930353
C 2.04642878204995 1.58046968796569 -7.75689677286187
H 2.64165746694522 0.66450259379877 -7.87345016849159
C 0.61398013251774 1.33182939498324 -8.22774818709359
H 0.00618061521147 2.21066341462945 -8.00123703844452
H 0.63342719272840 1.19542830107653 -9.30905330175776
C -0.01170350278054 0.09680201689898 -7.56902275847430
H -0.99991018174962 -0.07422139819565 -8.00321570099777
H 0.59522850927407 -0.79142894654210 -7.74543658128042
C -0.20391731468837 0.24996286030073 -6.07816602294153
O -0.56656951362843 1.26924623090592 -5.52904395253525
O 0.07651230024800 -0.85197850686983 -5.40944868670411
H -0.03322346330065 -0.72365221115436 -4.43581470429459
C 2.76247397315894 2.63134374644270 -8.64076809812744
O 2.93371357781350 2.44004621932724 -9.82533226016235
N 3.19188982589955 3.69338945917931 -7.94994810283632
H 2.87137325196567 3.83674188649450 -6.99757813138369
C 4.06940757040698 4.71461000111313 -8.46080578016875
H 3.84723347837246 4.86780100516172 -9.52443094160822
C 3.85874326210032 6.03203890048282 -7.69984607797341
H 4.39448511165028 6.80728485181738 -8.24796163659334
H 2.79465542134083 6.27637477734341 -7.70291567617606
C 4.38513613583926 6.03070574642916 -6.25902146898497
H 5.35926878619681 5.53736155251081 -6.21431859590763
H 4.54308266514681 7.05801174593375 -5.92357724596345
C 3.50426374233689 5.37211815382066 -5.22286963237071
O 2.53197506274388 4.68316305564676 -5.46896252295370
O 3.90687487646026 5.61196242961460 -3.99785026126321
H 3.33717473551388 5.13636972372648 -3.33162421595519
C 5.55865059867038 4.31784487047736 -8.38820982604577
O 6.40671869832384 5.00755798789611 -8.91211904321767
N 5.84287838899833 3.21424076774804 -7.67751635134534
H 5.14833477557178 2.61185360428599 -7.25716361916583
H 6.79986529695860 2.90140375010542 -7.66050208029754Протонированный октамер серина.
113
energy: -201.200454288451 gnorm: 0.000349374671 xtb: 6.4.1 (afa7bdf)
H 2.49721545567511 3.87807353982621 -2.10373174542101
C 3.16281417279585 3.74725458440091 -1.24880643684698
N 3.83702463349562 2.43569581364724 -1.32298315444157
H 4.20371443325490 2.16896202328098 -0.37351360950931
H 3.18030027649786 1.64749833907786 -1.60441167065734
C 4.23916822570882 4.82959307319177 -1.24915790994277
O 5.08760165047867 4.56906946559723 -2.35172020173377
C 2.35054397895232 3.78890037234317 0.08644987542851
O 1.26661960087190 4.37952621171734 0.08691752336123
O 2.88135217134677 3.17635750076514 1.02584212202439
H 4.61322035541361 2.51174457243903 -1.98579772764064
H 4.80562636609878 4.77886760353455 -0.30872600710979
H 3.76607204089641 5.81367334132308 -1.32474653112190
H 5.70645136433929 5.29636661968007 -2.45987723798086
H 3.20829950123256 -0.05747641890719 3.44526732799660
C 3.29981019705429 0.01337534431507 2.35653048121352
N 2.17596842197921 0.78651883588378 1.80061476514133
H 1.76771622390057 0.35952625875007 0.92049567795248
H 1.36033752032729 0.90369758782916 2.45253897489799
C 4.64253066048378 0.69413640491069 2.04998757990520
O 4.84964751901695 0.90459707722742 0.67683147992267
C 3.26870893453088 -1.43137960526447 1.79193114523526
O 4.33293667181094 -2.08546563793063 1.88422076663926
O 2.21027050613160 -1.84074335217258 1.30536801324578
H 2.49534034084887 1.76318408484188 1.55199485320604
H 5.44373683592769 0.07808834494143 2.47403034132272
H 4.66387179017436 1.68394186688039 2.51168907678390
H 4.77530214089143 0.05299766479406 0.20376869497328
H 4.34627744295081 -4.50291241648701 -1.70346567113234
H 4.80311698197755 -2.35242440445548 -2.48689355831693
O 1.79332058532581 -4.45978642294670 -0.63166319675425
C 2.45159503185966 -3.60448370901354 -1.27511454822625
H 0.44174865292810 -4.44684387965285 -0.90288321560308
O 2.02692972025436 -2.75884340927653 -2.05371399678423
C 3.99155958616541 -3.70771718301843 -1.03650388883453
H 5.75686361778671 -2.46691637716212 -0.98733014278608
C 4.74255559796512 -2.41679192317490 -1.39447410911826
N 4.16629407612984 -4.11788081842096 0.36985011209017
O 4.16831217737443 -1.25191861393614 -0.86852292180764
H 4.24803029037888 -3.18851033362617 1.08602033325789
H 3.33600173015800 -1.05441481426728 -1.33658390445168
H 3.29942626147140 -4.62247728180226 0.61681715445924
H -1.43697948457759 -0.44361554324839 -1.20374073080526
N -1.42758018675791 0.27129374531949 -1.95116078770133
H 0.42290313217275 -2.50956692268090 -2.41477519331804
H -2.21214348347591 0.09624525221836 -2.62365276875581
O -0.40968794597106 -2.12249601714518 -2.79080494070218
H -1.62915981934652 1.19698171502229 -1.50091475852402
O 2.15720058762874 0.48264090238060 -1.91293004594487
C 0.99589357642964 0.30603405889321 -1.50863482635187
C -0.11266319253073 0.27132666585669 -2.60558205146493
O 0.62000068419876 0.19363828497953 -0.33118614766590
C -0.03640957852923 -0.97089188525240 -3.50553994506247
H -0.74601777053982 -0.85446230346554 -4.33222528409508
H 0.00620207870559 1.16655731144449 -3.21992673077827
H 0.97251575405399 -1.07015533575885 -3.91031250753279
H -6.52514849173992 0.82131288674222 -2.02934965584556
O -3.75438010929788 0.21938736933524 -3.15901148649881
O -4.76419947439647 -1.31608782752079 -1.91348335154224
C -4.60085871508225 -0.16292177950159 -2.32923397177097
H -5.92073329667078 0.01619878266719 0.15233415397817
H -4.41740673780315 2.88038598666485 -1.47782022421482
C -5.48939208511112 0.97609808405358 -1.72144148763830
C -5.40867537030459 0.92290088012842 -0.19161638147107
H -5.91351787968797 1.79553580945509 0.22878838679987
H -1.78078017530516 4.99242076083042 0.97910068763602
O -4.05520805390194 0.88945981565956 0.21325370506026
H -2.47049540525808 3.97131552522911 3.21498326211370
C -2.97469433753058 3.75399681250443 2.26777276182580
H -3.77907797397780 4.48049218228185 2.12279082695980
N -4.94677932822516 2.24185765065250 -2.25239817916852
C -1.98249501303027 3.92682676146255 1.10576885425247
H -4.23187753835337 1.91648753877593 -2.94722358535149
H -3.93646404646704 1.49268065823515 0.98562142621181
C -2.61740011007749 3.38493927917956 -0.21293520506511
O -3.77023796821285 3.73527098869325 -0.50882347921201
O -1.89775334999391 2.59699170866989 -0.85015595442579
H 0.13714048117367 3.79416700702786 1.02406933593334
H -5.64493913028214 2.82639275604604 -2.70483078496326
N -0.71406888806120 3.18926048264046 1.27220186145062
H -0.73997775190703 2.49556716099633 0.48644285636043
O -3.58889421700796 2.49110664697202 2.30116782444436
H -1.90467957239945 -2.66830863864635 -2.21466826666196
H -3.02801517841942 1.83340974991089 2.78669559758190
N -2.82816991067722 -3.08206607623893 -1.91924595080366
H -2.99765824897870 -0.45375558172451 0.30037118437246
H -3.63541589522678 -2.34975124527838 -2.02790943779672
H -0.58371183912887 2.66462638729732 2.16579580286995
O -2.41051440792868 -1.23886784736241 0.21658403320385
H -2.99643693772948 -3.86914319968209 -2.54476069978587
C -2.76969668498845 -3.52574458143691 -0.50682270837636
O -0.63138096759990 -4.30724296749997 -1.15613651381904
C -1.34606535581226 -4.01172575260571 -0.13487373082076
H 0.67479146008330 -1.59161752651919 1.63789550151004
C -3.21941485445618 -2.39431169059112 0.42188128894048
H -4.26163622610150 -2.15925295238100 0.20295045910451
O -1.00509136078904 -4.06761808378402 1.02743505722431
O -2.19946814300413 0.50494127111523 3.30791506352948
H -3.45291618532441 -4.36533944299561 -0.35043537445245
N -0.31125151464534 -1.68005019433845 2.01988049987238
C -0.97865524623828 0.33325051774616 3.26809079279225
H -3.13417752636058 -2.72767792066418 1.46253749295904
O -0.12218881833789 1.22040331902679 3.07377865575680
C -1.43773524399172 -2.01958190981102 4.18272981964000
C -0.45659820145604 -1.13835824965481 3.39242848756380
H -0.98672712680734 -1.25265720154347 1.35622647268508
H -0.53154756339924 -2.69779203421901 1.99205871551490
H -1.53246236067088 -1.62187391525606 5.20213248187319
H 0.51614211569902 -1.14241654997257 3.89169472524213
H 4.98155197975694 -4.70794260851494 0.51877708415773
O -2.68469915885769 -2.10677248126307 3.55363072203881
H -1.04708422726705 -3.03962483310738 4.24064696080769
H -3.02922992675399 -1.19681154612842 3.50852539328317Уксусную кислоту мы уже видели на рисунках выше: там у нас происходит внутреннее вращение метильной группы относительно карбоксильной, это происходит из-за нежёсткости структуры этой молекулы: одинарная C—C связь такое вращение разрешает, а никакие внутримолекулярные взаимодействия водороды на месте особо не держат. Вот и получаем такой результат. Но остальная структура остаётся нежёсткой.

В случае с гексамером воды картина же ровно обратная. Посмотрев на молекулярную динамику достаточно долго, мы увидим постоянную перестройку структуры из водородных связей. Это же мы увидим и в распределении: непонятная беспонтовая.
А вот для двух наших «биологических» систем, такой структурной свободы мы не увидим. И трипептид GLH-GLH-GLH и октамер серина оказались достаточно жёсткими структурами, которым комнатные температуры не страшны. Все атомы оказались локализованы на своих местах, что в целом не удивительно, если бы такого не было, я бы этот текст не писал, а Вы его не читали бы впрочем, нагрев Земли из-за глобального потепления эту оплошность матушки-природы исправит.

Вместо заключения
Конечно, молекулярная динамика — это круто, и визуализации колебаний в виде облаков распределений — это весьма забавно. Но выше явно не хватило именно пошаговой последовательности того, что надо делать. Поэтому её я запихаю сюда.
-
Делаем молекулярную динамику нашей системы в программе XTB. Для этого в терминале запускаем команду
xtb ini.xyz --md --charge n, гдеn— это заряд нашей системы (0 для незаряженных, 1 для катиона, -1 для аниона, и т.д.). В результате получаем траекторию в файлеxtb.trj. Для дрругих фич и опций, RTFM. -
Полученную траекторию запихиваем в нашу программу, cubethemd.py. Для этого запускаем код в том же терминале как
python cubethemd.py -t xtb.trj --jmol. Список других опций у нас есть выше, или его можно увидеть командойpython cubethemd.py -h. В результате нам даются несколько файлов с разрешением.cube+ скрипт для Jmol (script.jmol). -
Этот файл script.jmol мы можем применить в Jmol. Для этого сначала открываем Jmol командой
jmol &в терминале. Потом открываем редактор скриптов (File -> Script Editor), вставляем туда содержимоеscript.jmolи нажимаем на кнопку «Run». Вуаля! Дальше эту картинку мы можем сохранить, экспортировать в PovRay и т.д. и т.п.
Спасибо за внимание :.
P.S.
Гифки с молекулярно-динамическими траекториями я строил способом, описанным в этой статье.
