Этот пост не является прямым продолжением вот этого, скорее он является следствием. Как раз тот случай, когда “после” — таки значит “вследствие”. В оригинальном посте утверждалось, что Вселенная виртуальна, что прошлое вычисляется на лету, а случайности — псевдослучайны (что даёт возможность вычислять будущее). Я так широко не замахиваюсь, я лишь хочу изложить свою точку зрения, чем, на мой взгляд, Вселенная похожа на экран дисплея. Абсолютно ненаучное изложение, пригодное лишь для размягчения айтишных мозгов, утомлённых «греблей на галерах”. Заранее прошу прощения у тех, чей интеллект почувствует себя оскорблённым чтением сего опуса — я пока ещё не научился мыслить красиво. Тех же, кто не боится запачкать себя “псевдонаукой” — прошу под кат. Не волнуйтесь, длинных формул не будет.
Ахиллес и черепаха
Да-да, они, родимые 🙂 Две с половиной тысячи лет назад греческий философ Зенон из Элеи (которая, как ни странно для греческого философа, ныне находится на территории Италии, чуть южнее Неаполя) сформулировал свои знаменитые апории, в которых отразил противоречия движения. Мне больше всего нравится апория “Ахиллес и черепаха”, суть которой можно свести к следующему:
Быстроногий Ахиллес никогда не догонит двигающуюся черепаху, если она была на некотором расстоянии от него, потому что пока Ахиллес будет пробегать это расстояние, черепаха проползёт вперёд ещё на чуть-чуть и Ахиллесу опять придётся догонять черепаху, которая опять от него уползёт.
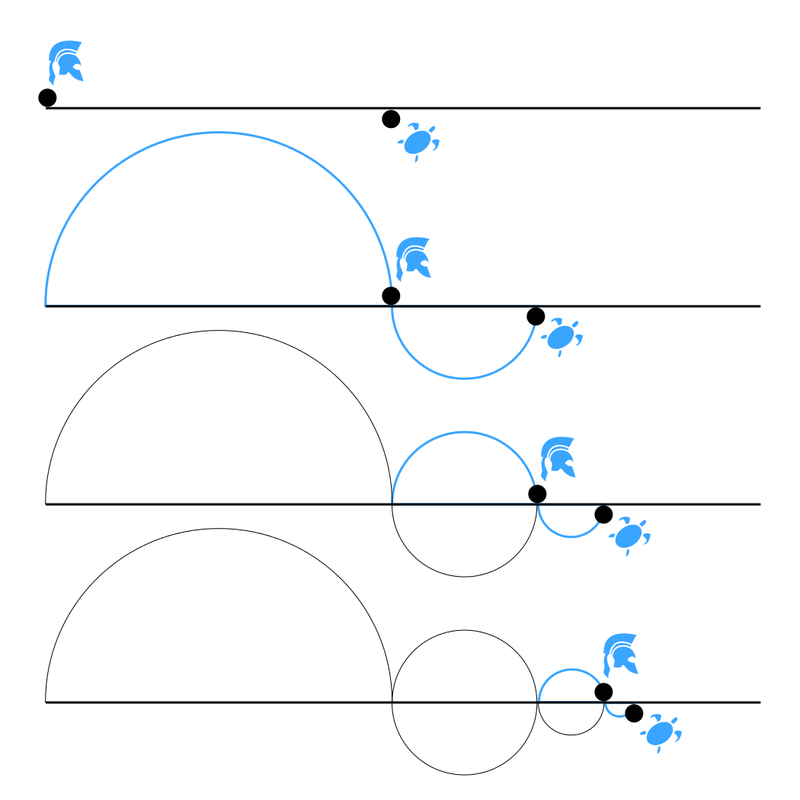
В общем, если размышлять абстрактно, то Зенон прав — черепаха всегда будет на “чуть-чуть” впереди Ахиллеса, а если смотреть на практике, то Зенон не прав — Ахиллес делает черепаху без напряга.
Практический эксперимент показывает, что теоретические выкладки имеют некий изъян. И этот изъян в том, что Зенон в своей апории полагает, что цикл “черепаха убежала, пока Ахиллес догоняет” бесконечный. Но так как Ахиллес всё-таки черепаху догоняет и перегоняет, то можно сделать вывод, что цикл в какой-то момент прерывается.
Что есть какое-то очень маленькое расстояние, меньше которого уже не может быть (квант пространства), которое Ахиллес преодолевает за некий промежуток времени, а черепаха за тот же самый промежуток времени — нет. Или наоборот, есть какой-то маленький промежуток времени, меньше которого уже не может быть (квант времени), который разбивает путь Ахиллеса и черепахи на очень маленькие, но не бесконечно маленькие кусочки, пропорциональные их скорости. И в какой-то момент общая длина этих кусочков у Ахиллеса превысит общую длину аналогичных кусочков у черепахи.
В общем, Зенон практически пальцем указал на то, что бесконечность в малом отсутствует. Что либо пространство, либо время, либо и то, и то — квантуемо.
Что такое движение?
С философской точки зрения движение — это вообще любое изменение. Но если мы рассматриваем движение в рамках данной апории (с точки зрения механики), то движение — это перемещение объектов (Ахиллеса и черепахи) относительно чего-то (точек старта) с течением времени.
В понятии “движение” собраны воедино понятия “пространство” и “время”. Со временем на обывательском уровне всё более-менее понятно — все мы пользуемся секундами и производными от них. С пространством же ситуация чуть более запутанная. Помимо размеров (метры, футы, дюймы, …) есть ещё и размерность — 2D, 3D, а некоторые даже время умудрились вплести в пространство, доведя размерность до 4D. В рамках данной публикации я буду придерживаться модели обычного Евклидова пространства (трёхмерного) и измерять величины в метрах. Размеры объектов для упрощения умозаключений буду брать минимально возможные: и Ахиллес, и черепаха — точки в пространстве. Для определения местоположения точек в пространстве использую Декартову систему координат.
В общем, получается, что движение — это изменение с течением времени координат точек, представляющих собой местоположение Ахиллеса и черепахи в пространстве.
Так вот, апория Зенона показывает, что:
-
в случае квантования пространства: количество точек на ограниченном пространстве (допустим, 1 кубический метр), где могли бы находиться Ахиллес или черепаха, ограничено;
-
в случае квантования времени: ограничено количество достижимых точек пространства — мы можем поместить Ахиллеса или черепаху только в те точки пространства, координаты которых равны произведению скорости каждого из них на количество квантов времени, прошедших с момента старта.
Что такое время?
Мы исчисляем время в секундах, а секунду определяем как:
интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями энергии основного состояния атома цезия-133, находящегося в покое при 0 К
У нас нет другого способа измерить время, кроме как относительно какого-то периодического процесса — вращение Земли вокруг оси (сутки) или вокруг Солнца (год), Луны вокруг Земли (лунный месяц). Или излучению атома цезия (секунда).
То есть время — это изменение, движение в философском смысле. В мире, где ничего не изменяется, времени не существует. В какой-то мере время вторично по отношению к пространству. Именно изменения в пространстве порождают время, без пространства времени не существует.
Если рассматривать вариант с квантованием пространства/времени для выхода из апорийного парадокса Зенона, то придётся допустить существование некоего самого высокочастотного процесса во Вселенной (например — изменение координат фотоном). Процесса, где изменения происходят за один “тик” (за один квант времени). Длительность всех остальных процессов будет измерятся в этих “тиках”.
В компьютерных процессорах подобный, самый высокочастотный, процесс называется тактовой частотой. Самые быстрые операции в процессоре (например, сдвиг или сложение) выполняются за один такт, более сложные операции (например, с плавающей точкой) могут требовать большее количество тактов. В реальности всё несколько сложнее, например, возможно умножение частоты тактового генератора, но в любом случае, в процессоре существует самый высокочастотный процесс и работа всего процессора синхронна относительно этого процесса.
В контексте процессоров наше привычное время — штука довольно относительная и зависит от частоты тактового генератора. Один и тот же процессор требует разного привычного нам времени на выполнение последовательности операций в своём (а) обычном и (б) разогнанном состояниях, но в обоих случаях количество тактов (тиков) на выполнение последовательности будет одинаковым (что характерно, иногда время в контексте процессоров подменяется пространством — «короткие и длинные операции«).
Равномерность времени
Давайте посмотрим из нашего физического мира (где одна секунда равна 9 192 631 770 периодам излучения атома цезия) на игру “Арканоид”, выполняемую на компьютере, допустим, с 486-м процессором и с тактовой частотой 16 МГц. Пусть мы можем изменять тактовую частоту процессора в некоторых пределах. С нашей точки зрения (внешнего наблюдателя) мы видим, как шарик (и всё остальное) движется то быстрее, то медленнее, но с точки зрения самого шарика никаких изменений в скорости не фиксируется. Ему нужно одно и то же количество тактов для того, чтобы сдвинуться на один пиксель, при любых изменениях тактовой частоты процессора.
Мы можем даже увести компьютер в состояние “сна” (гибернации), включить его на следующий день, а шарик в Арканоиде даже не заметит, что было какое-то прерывание. Нет никакого способа, находясь внутри “компьютера”, удостовериться в равномерности и непрерывности течения “времени”. Если кто-то (допустим, Бог — обожаю эту гипотезу!) переведёт нашу Вселенную в режим гибернации, то мы этого даже не заметим. Бог может разобрать всю Вселенную до винтика, почистить, собрать обратно в том же порядке, запустить, а мы, в лучшем случае, начнём говорить про эффект Манделы.
Равномерность движения
Я надеюсь, что к данному моменту у вас сложилось понимание, что на микроуровне бесконечность деления отсутствует и время и пространство состоят из мельчайших неделимых частиц (квантов).
В своей апории “Стрела” Зенон утверждает следующее:
Летящая стрела неподвижна, так как в каждый момент времени она занимает равное себе положение, то есть покоится; поскольку она покоится в каждый момент времени, то она покоится во все моменты времени, то есть не существует момента времени, в котором стрела совершает движение.
Действительно, если пространство/время квантуемо, то переход от одного положения стрелы к другому происходит мгновенно, скачком, и в следующий квант времени стрела опять находится в неподвижности. Сколько времени занимает операция сдвига в процессоре? Один такт. Что существует между тактами? С точки зрения самой операции сдвига — ничего. А что происходит в течение такта? Опять же ничего, с точки зрения операции.
Равномерность движения в реальном мире — это иллюзия. Точно такая же, как движение в кинофильме. Она создаётся быстрой сменой отдельных кадров. Если мы допускаем квантование пространства/времени, то мы приходим к тому, что в каждый момент времени (квант времени) тела находятся в определённых точках пространства, а в следующий момент времени они исчезают в тех точках, где были, и появляются в новых. Последовательное исчезание/появление создаёт иллюзию движения.
На уровне квантов пространства мы постоянно исчезаем в одном месте и появляемся в другом. Фактически происходит пересборка всей Вселенной, ну или, с учётом оптимизаций, только тех её частей, где нужны изменения.
Квант пространства
Размер отдельного кванта пространства в настоящее время не определён, но принято считать, что он не больше, чем Планковская длина (1.6 * 10^-35 м) в кубе. Т.е., в одном кубическом метре пространства помещается примерно 4 * 10^105 квантов. Для сравнения, объём наблюдаемой Вселенной — 3.5⋅10^80 м3. Т.е. в одном кубическом метре квантов пространства на 25 порядков больше, чем кубических метров в наблюдаемой Вселенной. И это как минимум!
В общем, как говорилось в одной житейской мудрости: “вам может показаться, что я ничего не делаю, но на клеточном уровне я очень занят”. Процессы, которые происходят на уровне квантов пространства, может быть и не очень сложные, но их чертовски много. По сути, нужно пересобирать всю Вселенную на каждом “тике” (ну, или хотя бы её изменяющиеся части).
Кстати, реальные физики и математики уже делают некоторые успехи в объединении Теории Относительности и Квантовой механики — например, теория Петлевой квантовой гравитации.
Очень Большой Дисплей
Айтишники и геймеры, которые читают этот пост, уже поняли, чем Вселенная, при таком рассмотрении, похожа на экран дисплея. У дисплея есть пиксели (кванты пространства), есть плотность пикселей (кванты на единицу объёма), есть разрешение (кол-во квантов по актуальным высоте, ширине и глубине). Есть даже частота кадров (FPS). Для игровых персонажей, отображаемых на экране дисплея, время существует в виде непрерывного однонаправленного потока, для внешнего же наблюдателя игровое время может быть прервано или даже отмотано назад — на ближайшую сохранёнку. Нарисованные персонажи подчиняются законам игрового мира и не могут пройти через нарисованную стену (если только игровой мир не подразумевает наличие чит-кодов), хотя одни и те же пиксели дисплея могут отображать, как персонаж, так и стену — в зависимости от того как мы развернём камеру в игре.
На самом деле, и персонажи, и окружение — всё это существует не на экране дисплея. И персонажи, и окружение, и законы игры — всё это существует в памяти компьютера в виде электрических сигналов. Экран дисплея существует лишь для визуализации происходящего в игре для внешнего наблюдателя. Вполне допускаю, что алгоритмы перерасчёта состояния нашей Вселенной находятся вне устройства “отображения информации” (пространства). Но если законы игры позволяют персонажам осознавать себя и анализировать своё игровое окружение, то у персонажей есть шанс узнать не только законы своей игры, но и некоторые из законов “внешнего” мира. А может даже законтактировать со своими Создателями.
Резюме
Вселенная существует вне зависимости от нашего о ней мнения. Все наши модели (строгие и не очень) всего лишь описания нашего представления о ней. Некоторые лучше, некоторые хуже. С различными границами применимости (как ньютоновская механика). Наше представление о реальности ограничено нашими возможностями. Слепому от рождения трудно, если не невозможно, понять концепцию цвета, но цвет существует вне зависимости от возможности его познать. Наши модели реальности — это наши попытки описания цвета слепым. Зачастую, они говорят не столько о том, что моделируют, сколько о том, кто моделирует. Возможно принцип неопределённости Гейзенберга относится не столько к самой Вселенной, сколько к нашей собственной способности её познать. Ведь мы, как ни крути, тоже являемся частью Вселенной.
Спасибо всем, кто дочитал до конца, и отдельное спасибо @igor_zvyagin за его статью и всем комментаторам его статьи за их комментарии.


