Физики нашли алгебраическую структуру, лежащую в основе запутанной математики столкновений элементарных частиц. Некоторые надеются, что она приведёт нас к более элегантной теории физического мира.
Когда специалисты по физике частиц пытаются моделировать эксперименты, они сталкиваются с невозможными расчётами из-за бесконечно большого уравнения, работа с которым лежит за пределами возможностей современной математики.
К счастью, они могут выдавать в целом точные предсказания, не прорабатывая всю эту загадочную математику до конца. Укорачивая вычисления, учёные с Большого адронного коллайдера в европейском ЦЕРН делают предсказания, совпадают с событиями, которые они потом наблюдают при столкновениях субатомных частиц, несущихся с огромной скоростью по 26-километровому треку.
К сожалению, эпоха согласия между предсказаниями и наблюдениями может подходить к концу. Чем точнее становятся измерения, тем сложнее поспевать за ними схемам приближённых вычислений, которые используют теоретики.
«Мы уже близки к исчерпанию имеющихся у нас средств», — сказал Клод Дар, специалист по физике частиц из ЦЕРН.
Однако три недавних работы за авторством Пьерпаоло Мастролия из Падуанского университета в Италии и Себастьяна Мизеры из Принстоновского института передовых исследований в Нью-Джерси, открыли математическую структуру, лежащую в основе этих уравнений. Она даёт новый способ схлопывания бесконечного количества членов до десятка необходимых компонентов. Их метод может помочь вывести точность предсказаний на следующий уровень, который необходим теоретикам для того, чтобы выйти за рамки лидирующей, но не полной модели физики частиц.
«Они показали множество результатов, доказывающих жизнеспособность этой многообещающей техники», — сказал Дар.
Однако преимущества могут оказаться гораздо большими, чем простое улучшение предсказаний. Новый метод обходит традиционные муторные математические вычисления, напрямую подсчитывая «числа пересечения», что, как считают некоторые, может в итоге дать нам более элегантное описание субатомного мира.
«Это не просто математика», — сказал Саймон Карон-Хьюот из Университета Макгилла, специалист по квантовой теории, изучающий последствия работы Мастролия и Мизеры. «Это всё очень глубоко переплетено с квантовой теорией поля».
Бесконечная петля
При моделировании столкновений частиц физики используют диаграммы Фейнмана – простую запись, изобретённую Ричардом Фейнманом в 1940-х.
Чтобы понять, как эта запись работает, рассмотрим простое событие: сближаются два кварка, обмениваются одним глюоном в процессе «столкновения», а потом отскакивают друг от друга по разным траекториям.
На диаграмме Фейнмана пути кварков обозначаются «ногами», которые в месте стыка формируют «вершины» во время взаимодействия частиц. Фейнман разработал правила превращения такого рисуночка в уравнения, вычисляющие вероятность наступления этого события. Пишете особую функцию для каждой ноги и вершины – обычно это дробь с использованием массы и импульса частицы – и перемножаете всё это. Для таких простых вариантов, как наш, вычисления могут уместиться на салфетке.
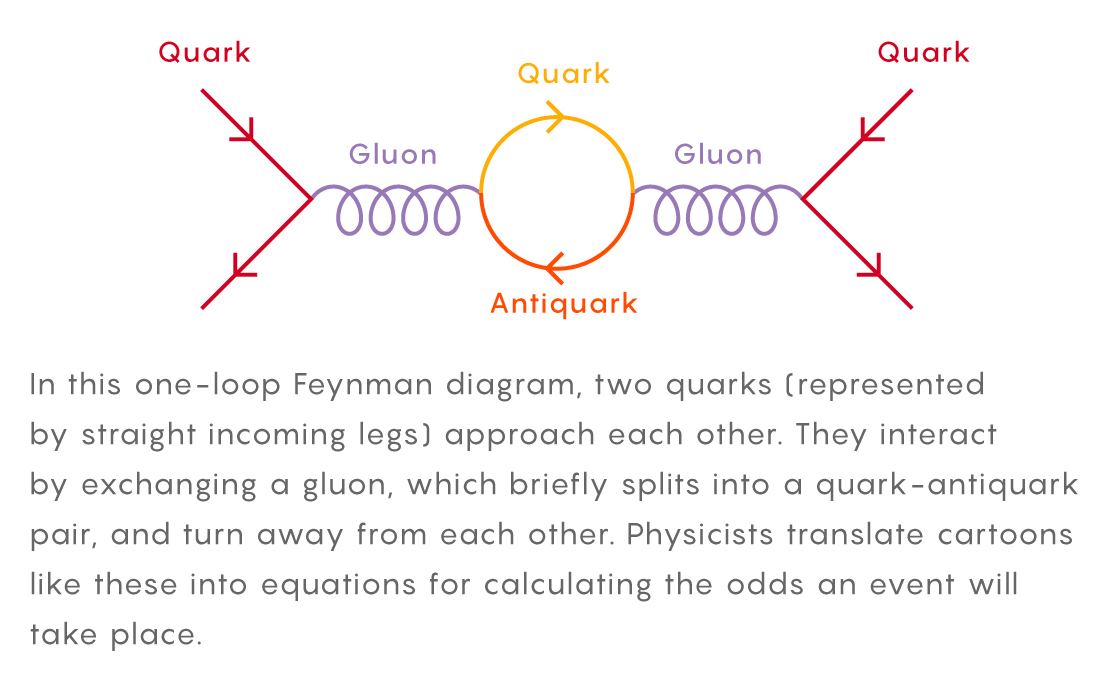
В данной диаграмме с одной петлёй сближаются два кварка (обозначенные прямыми ногами со стрелками, направленными внутрь). Они взаимодействуют, обмениваясь глюоном, который на краткий промежуток времени расщепляется на пару кварк-антикварк, а потом разлетаются в стороны. Физики переводят такие рисуночки в уравнения, вычисляющие вероятность наступления этого события.
Однако золотое правило квантовой теории – рассматривать все возможности, и обмен простым глюоном представляет собой лишь один из огромного разнообразия сценариев, которые могут развернуться при столкновении двух кварков. Глюон, которым обмениваются частицы, может на краткий промежуток времени расщепиться на пару кварк-антикварк, а потом вновь превратиться в глюон. Встречаются два кварка и расходятся два кварка, но в промежутке может произойти много всего. Для полного учёта происходящего, дающего идеальное предсказание, потребуется нарисовать бесконечное количество диаграмм. Никто не ждёт идеальных результатов, однако ключ улучшения точности вычислений – пройти как можно дальше по бесконечной цепи событий.
И вот тут физики застревают.
Чтобы подробнее изучить этот скрытый центр, нужно обращаться к виртуальным частицам – квантовым флуктуациям, исподволь влияющим на результат каждого взаимодействия. Кратковременное существование пары кварков, упомянутой выше, как и многие виртуальные события, обозначается на диаграмме Фейнмана замкнутой петлёй. Петли ставят физиков в тупик – это чёрные ящики, прибавляющие дополнительные слои к бесконечным сценариям. Чтобы как-то подсчитать возможности, подразумеваемые петлёй, теоретикам нужно брать интегралы. Эти интегралы достигают чудовищных размеров в диаграммах Фейнмана со многими петлями, которые появляются по мере того, как исследователи движутся всё дальше по цепочке событий, и учитывают всё более сложные виртуальные взаимодействия.
У физиков есть алгоритмы для вычисления вероятностей реализации сценариев без петель или с одной петлёй, однако уже столкновения с двумя петлями ставят компьютеры на колени. Это потолок предсказательной точности – и понимания физиками последствий квантовой теории.
Однако у всего этого есть одна положительная сторона: физикам не нужно вычислять абсолютно все интегралы сложной диаграммы Фейнмана, поскольку большую часть из них можно собрать в один.
Тысячи интегралов можно свести к нескольким десяткам «основных», которым можно задать веса и сложить. Но какие интегралы можно собрать в отдельные основные – сложный вычислительный вопрос. Исследователи используют компьютеры, которые, по сути, выдают догадки на основе миллионов взаимодействий и с трудом извлекают значимые комбинации интегралов.
Однако благодаря числам пересечений физики, возможно, нашли способ элегантно выбирать важную информацию из расползающихся расчётов фейнмановских интегралов.
Геометрический отпечаток пальца
Работа Мастролиа и Мизеры растёт из такого ответвления математики, как алгебраическая топология, классифицирующего формы и пространства. Помогают в этом теории «когомологии«, позволяя вычислять алгебраические «отпечатки пальцев» из сложных геометрических пространств.
«Это что-то вроде конспекта, алгебраического приспособления, включающего в себя суть пространства, которое вы изучаете», — сказал Клемент Дюпон, математик из университета Монпелье во Франции.
Диаграммы Фейнмана можно перевести в геометрические пространства, которые затем можно анализировать при помощи когомологии. Каждая точка такого пространства может обозначать один из множества сценариев, разворачивающихся при столкновении частиц.
Мы могли бы понадеяться, что взяв когомологию этого пространства – найдя его алгебраическую структуру – вы могли бы подсчитать веса для основных интегралов. Однако геометрическое пространство, характеризующее большинство диаграмм Фейнмана, настолько искривлено, что сопротивляется множеству когомологических вычислений.
В 2017 году Мизера пытался анализировать столкновения объектов в теории струн, когда наткнулся на инструменты, которые впервые изобрели Израиль Гелфанд и Кацухико Аомото в 1970-х – 1980-х годах, когда работали над когомологией под названием «перекрученная когомология». Позднее, в том же году Мизера познакомился с Мастролиа, который понял, что эти техники могут сработать и на диаграмме Фейнмана. В прошлом году они опубликовали три работы, использовавшие теорию когомологии для ускорения вычислений простых столкновений частиц.
Их метод берёт семейство взаимосвязанных физических сценариев, представляет его в виде геометрического пространства, и вычисляет его перекрученную когомологию. «И эта перекрученная когомология сообщает об интересующих нас интегралах всё», — сказал Мизера.
В частности, перекрученная когомология сообщает, сколько потребуется основных интегралов и каковы должны быть их веса. Эти веса проявляются как значения, которые они называют «числами пересечения». В итоге тысячи интегралов усыхают до взвешенной суммы из нескольких десятков основных.
Возможно, что теории когомологии, выдающие эти числа пересечения, смогут сделать больше, чем простое облегчение вычислений – они могут указать нам на физическую значимость наиболее важных величин в вычислениях.
К примеру, когда виртуальный глюон распадается на два виртуальных кварка, их времена жизни могут быть разными. В связанном с ними геометрическом пространстве каждая точка может обозначать различное время жизни кварка. При подсчёте весов исследователи видят, что сценарии с наиболее долгоживущими виртуальными частицами – то есть, те случаи, в которых частицы становятся почти настоящими – сильнее других влияют на результат.
«Вот, что удивительно с этим методом, — сказал Карон-Хьюот. – Он воссоздаёт все, начиная с этих редких, особых событий».
На прошлой неделе Мизера, Мастролиа и их коллеги опубликовали ещё один препринт, где показано, что эта техника развилась достаточно для того, чтобы работать с реальными диаграммами с двумя петлями. В следующей работе Карон-Хьюот разовьёт этот метод ещё дальше, возможно, укротив даже диаграммы с тремя петлями.
В случае успеха эта техника сможет помочь открыть новое поколение теоретических предсказаний. И, как подозревают некоторые исследователи, даже может продемонстрировать нам новый взгляд на реальность.


