Математическая продлёнка: Изучаем гиперболические числа

Вчера в 21:33

В этой серии статей мы рассматриваем различные необычные виды арифметик, которые получаются из привычных числовых систем их расширением. В качестве расширения используется решение некоторого уравнения, не решаемого в исходной системе, а новая арифметика состоит из линейных комбинаций «обычных» чисел и «необычного» расширения.

Оглавление серии

В третьей части мы нащупали конструктивный способ строить новые арифметики с помощью расширения уже известных числовых систем. Расширение подразумевает добавление в систему элемента, которого там не существует, и который можно считать линейно независимым по отношению к любому элементу в этой системе.

Линейная независимость двух величин и y означает, что их линейная комбинация может быть равна нулю, только если равны нулю оба коэффициента и . На этом этапе уже можно запутаться. Если все величины и принадлежат одной арифметике, то есть представляют собой однородные числа, то как различить кто на кого умножается и кто от кого независим?

Поначалу мы использовали пары, которые создавали эти две независимые компоненты «векторным» образом. Действительно, двумя ортогональными, то есть, независимыми базисными компонентами арифметики могли бы быть элементы и , которые, в линейной комбинации давали любое число:

Этот абсолютно векторный подход ничего не говорит нам о свойствах базисных элементов, которые «навешиваются» искусственно через определение специфической операции умножения.

Развивая линейный подход к арифметике, мы пришли к тому, что начали рассматривать элементы арифметики, уже не как векторы или точки, а как линейные преобразования, или действия над ними. Тогда композиция этих действий будет представлять произведение элементов арифметики, а вместо чисел можно рассматривать матрицы, представляющие линейные преобразования. Таким образом, вся информация о свойствах базовых элементов и, соответственно, всей арифметики, заключается в матрицах, представляющих эти элементы.

В качестве примеров, мы рассмотрели представления целых и гауссовых чисел, в которых один элемент это единичная матрица, представляющая элемент расширяемой арифметики, а второй, расширяющий элемент это матрица с необходимыми мультипликативными свойствами. В случае расширения натуральных чисел до целых, это матрица

$j=\left(\begin{matrix}0 & 1\\1 & 0\end{matrix}\right),$

которая представляет число . А в случае гауссовых чисел это матрица

$i=\left(\begin{matrix}0 & -1\\1 & 0\end{matrix}\right),$

которая при возведении в квадрат даёт единичную матрицу, умноженную на , и таким образом, представляет мнимую единицу.

А какие ещё осмысленные арифметики можно построить, из линейной комбинации единичной матрицы и матрицы общего вида

$\left(\begin{matrix}0 & a\\b & 0\end{matrix}\right),$

в которой числа и принадлежат какой-то числовой системе? Все такие матрицы имеют одно важное свойство, при возведении в квадрат, они порождают матрицу, пропорциональную единичной:

$\left(\begin{matrix}0 & a\\b & 0\end{matrix}\right)\left(\begin{matrix}0 & a\\b & 0\end{matrix}\right) = \left(\begin{matrix}ab & 0\\0 & ab\end{matrix}\right) = ab\left(\begin{matrix}1 & 0\\0 & 1\end{matrix}\right).$

Таким образом, эти матрицы представляют решения уравнения: в которой произведение присутствует в арифметике, а какой-либо из корней этого квадратного уравнения в ней найти невозможно.

В частности, с помощью матриц такого вида можно добавить к целым числам корень из любого целого, не являющегося квадратом. Скажем, так может выглядеть целочисленная матрица, представляющая $\sqrt 2$ :

$\left(\begin{matrix}0 & 2\\1 & 0\end{matrix}\right).$

А так с её помощью строится представление для расширения целых чисел $ℤ(\sqrt 2)$ :

$\left(\begin{matrix}a & 2b\\b & a\end{matrix}\right) \sim a+b\sqrt 2\quad a,b\in \mathbb{Z}.$

Широкого практического применения такие арифметики не имеют, и встречаются в основном, в задачниках по теории чисел или теории Галуа, но, по крайней мере, теперь понятно, откуда взялись матрицы, представляющие и , как корни соответствующих квадратных уравнений.

Двойные числа

Уравнение имеет два очевидных корня . Когда мы строили кольцо целых чисел из полукольца натуральных, мы использовали отношение эквивалентности и факторизовали с его помощью арифметику для пар. А что если отказаться от факторизации и расширить поле вещественных чисел с помощью элемента

$j=\left(\begin{matrix}0 & 1\\1 & 0\end{matrix}\right),$

то есть, построить такое расширение:

$x+yj \sim \left(\begin{matrix}x & y\\y & x\end{matrix}\right).$

От представления целых чисел, это, как кажется, ничем не отличается, но теперь все элементы матрицы могут быть вещественными числами, а не только натуральными. Такие числа называют двойными, паракомплексными или гиперболическими числами. Вот как выглядит арифметика двойных чисел:

$\begin{matrix}(x+yj) + (s+tj) = (x+s) + (y+t)j\\(x+yj) \times (s+tj) = (xs+yt) + (xt+ys)j\end{matrix}$

Сразу скажу, что какими-то удивительными свойствами эта арифметика вас не поразит. Больше всего меня удивляет разнообразие названий этих числах. Только в Википедии перечислено без малого два десятка разных синонимов двойных чисел.

(real) tessarines, James Cockle (1848)
(algebraic) motors, W.K. Clifford (1882)
hyperbolic complex numbers, J.C. Vignaux (1935), G. Cree (1949)
bireal numbers, U. Bencivenga (1946)
real hyperbolic numbers, N. Smith (1949)
approximate numbers, Warmus (1956),
double numbers, I.M. Yaglom (1968), Kantor and Solodovnikov (1989), Hazewinkel (1990), Rooney (2014)
hyperbolic numbers, W. Miller & R. Boehning (1968), G. Sobczyk (1995)
anormal-complex numbers, W. Benz (1973)
perplex numbers, P. Fjelstad (1986) and Poodiack & LeClair (2009)
countercomplex or hyperbolic, Carmody (1988)
Lorentz numbers, F.R. Harvey (1990)
semi-complex numbers, F. Antonuccio (1994)
paracomplex numbers, Cruceanu, Fortuny & Gadea (1996)
split-complex numbers, B. Rosenfeld (1997)
spacetime numbers, N. Borota (2000)
Study numbers, P. Lounesto (2001)
twocomplex numbers, S. Olariu (2002)
split binarions, K. McCrimmon (2004)

Это говорит о разнообразии применения этой числовой системы. И действительно, она используется в ряде приложений от теории вычислений до геометрической алгебры и от квантовой физики до релятивистской механики. В частности, преобразования Лоренца очень естественно формулируются как поворот в гиперболической плоскости, которую называют пространством Минковского.

Нас в контексте знакомства с числовыми системами должно заинтересовать то, что двойные числа оказались, по какой-то причине, связаны с целыми числами (см. «Изобретаем целые числа»). Как уже упоминалось, даже если мы построим арифметику двойных чисел на базе полноценного числового поля, она будет неполноценной, поскольку в ней есть необратимые элементы и делители нуля. Действительно, для любых значений и :

что не даёт этой арифметике быть областью целостности. А теперь вспомним, что когда мы определяли кольцо целых чисел, как множество пар натуральных чисел, то вводили отношение эквивалентности, $(n + a, n + b) \sim (a, b)$ , которое пару одинаковых элементов отождествляли с нулём. Таким образом, мы можем заключить, что кольцо целых чисел — это кольцо двойных чисел над натуральными числами, факторизованное множеством делителей нуля вида .

В двойных числах можно определить два любопытных элемента, которым не соответствуют никакие привычные нам числа:

$u_+=\frac12(1+j),\quad u_-=\frac12(1-j).$

Они примечательны тем, что являются решениями уравнения (идемпотентны для умножения) наряду с вещественными решениями и . При этом произведение этих элеменов равно нулю, что тоже делает их нетривиальными делителями нуля. Любое двойное число можно однозначно представить как линейную комбинацию идемпотентных элементов:

В этом представлении кольцевые арифметические действия становятся чрезвычайно простыми — все доступные арифметические действия становятся поэлементными:

$(xu_+ + yu_-) \pm (su_++tu_-) = (x\pm s)u_+ + (y\pm t)u_-\\(xu_++yu_-) \times (su_++tu_-) = (xs)u_+ + (yt)u_-\\(xu_+ + yu_-)^{-1}=\frac1x u_+ + \frac1y u_-$

Отсюда следует, что двойные числа изоморфны прямому произведению вещественных чиcел $\mathbb{R}\times\mathbb{R}$ . C одной стороны, это обстоятельство делает их менее интересными, а с другой — даёт им полезную интерпретацию, подмеченную польским математиком Мечеславом Вармусом. В небольшой статье, опубликованной в 1956 году, он использует двойные числа для представления одного из практических вариантов арифметики интервалов. Действительно, однородный интервал можно представить числом , а приближенное значение числа $x \pm \Delta$ как число $x + \Delta j$ . При этом арифметика двойных чисел будет давать практичную и эффективную реализацию арифметики интервалов, с известными ограничениями. К достоинствам такого представления интервальной арифметики можно отнести наличие в ней гиперболических аналогов формул Эйлера и Муавра, которые как и для комплексных чисел, позволяют эффективно выражать произведения и степенные функции от интервалов.

Я не большой фанат интервальной арифметики и погружаться в эту тему глубже, чем она описана у Вармуса, не стану. Как физику и матмоделисту, мне ближе классический анализ погрешностей, базирующийся на производных, на моё счастье именно такие вычисления вместе с автоматическим дифференцированием успешно моделируют параболические дуальные числа, о которых мы поговорим в следующей статье.

Формула Бине

Завершая рассказ о гиперболических арифметиках, я хочу порассуждать о том, каким волшебным образом появляется и почему работает известная формула Бине:

$F_n=\frac{\left(\frac{1+\sqrt5}{2}\right)^n - \left(\frac{1-\sqrt5}{2}\right)^n}{\sqrt5},$

которая позволяет в конечной форме вычислять целые числа Фибоначчи. На неискушённый взгляд, она вызывает недоумение: почему иррациональные корни из пяти, при возведении в какие-то целые степени должны давать целые числа, которые описываются простой последовательностью:

$F_n=F_{n-1}+F_{n-2}, \quad F_0 = 0,\quad F_1 = 1.$

Рассмотрим одну числовую систему гиперболического типа, расширяющую целые числа решением целочисленного уравнения . Корни этого уравнения вещественные, но иррациональные и равны:

$\frac{1+\sqrt5}{2}=\Phi, \quad \frac{1-\sqrt5}{2}= -1/\Phi.$

Число $\Phi$ называется золотым сечением и получило широкую известность за пределами математики как нечто невероятно загадочное, красивое и практически непостижимое, в общем, звезда математической попкультуры.

В этой серии статей мы отыскиваем матричные представления для всяких особенных чисел, так что давайте посмотрим на матричное представление золотого сечения. Это должна быть матрица со следом и определителем, равным и , соответственно, тогда её характеристическое уравнение совпадёт с уравнением золотого сечения. Простейшими целочисленными матрицами с такими свойствами будет такая пара:

$\Phi \sim \left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right),\quad -1/\Phi \sim \left(\begin{matrix}1 & -1\\-1 & 0\end{matrix}\right).$

Можно убедиться в том, что это именно они, вспомнив, что разность корней уравнения золотого сечения должна быть равна $\sqrt 5$ . Действительно, если мы вычислим эту разность и возведëм в квадрат, то получим матричное представление вещественного числа :

$\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right) - \left(\begin{matrix}1 & -1\\-1 & 0\end{matrix}\right) = \left(\begin{matrix}-1 & 2\\2 & 1\end{matrix}\right)\\ \left(\begin{matrix}-1 & 2\\2 & 1\end{matrix}\right) \left(\begin{matrix}-1 & 2\\2 & 1\end{matrix}\right) = \left(\begin{matrix}5 & 0\\0 & 5\end{matrix}\right)$

Поскольку собственные числа этих матриц вещественные, мы, действительно, имеем дело с числовой системой гиперболического типа. Если расширить с помощью матрицы $\Phi$ кольцо целых чисел, то получится кольцо $ℤ(\Phi)$ , с элементами, имеющими вид:

$a + b\Phi \sim \left(\begin{matrix}a & b\\b & a+b\end{matrix}\right).$

В отличие от чисел Гаусса или Эйзенштейна, они не имеют геометрического представления в виде регулярной решётки, замкнутой относительно преобразований, соответствующих сложению и умножению таких чисел. Но алгебраически это полноценное кольцо, имеющее в качестве подкольца целые числа.

Давайте внимательнее присмотримся к матрице $\Phi$ и посмотрим на то, как она действует сама на себя:

$\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right) \sim \Phi\\\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right)\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right) = \left(\begin{matrix}1 & 1\\1 & 2\end{matrix}\right) \sim \Phi^2\\\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right)\left(\begin{matrix}1 & 1\\1 & 2\end{matrix}\right) = \left(\begin{matrix}1 & 2\\2 & 3\end{matrix}\right) \sim \Phi^3\\\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right)\left(\begin{matrix}1 & 2\\2 & 3\end{matrix}\right) = \left(\begin{matrix}2 & 3\\3 & 5\end{matrix}\right) \sim \Phi^4\\\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right)\left(\begin{matrix}2 & 3\\3 & 5\end{matrix}\right) = \left(\begin{matrix}3 & 5\\5 & 8\end{matrix}\right) \sim \Phi^5$

Внимательный читатель легко разглядит в результатах умножения числа Фибоначчи, которые, как известно, тесно связаны с золотым сечением. Легко увидеть, откуда они тут взялись, если посмотреть на то, как матрица $\Phi$ действует на произвольный вектор:

$\left(\begin{matrix}0 & 1\\1 & 1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right) = \left(\begin{matrix}y\\x+y\end{matrix}\right).$

Это же и есть элементарный шаг в последовательности Фибоначчи:

$(x,y) \to (y,x+y),$

его можно было сразу разглядеть в приведённом выше представлении для числа $a + b\Phi$ . С помощью такого шага последовательность Фибоначчи, как правило, и программируют. Вот, например, простейшая программка на языке Julia, вычисляющая -ное число Фибоначчи:

function fib(n) :: BigInt
  (x,y) = BigInt.((0,1))
  for i ∈ 1:n
    (x,y) = (y,x+y)
  end
  return x
end

Выходит, что матрица, которая представляет золотое сечение, напрямую задаёт алгоритм вычисления чисел Фибоначчи! Красивая связь, правда? А как, зная это, можно выразить -ное число Фибоначчи через золотое сечение? Отметим, сначала, что

$\Phi^n \sim \left(\begin{matrix}F_{n-1} & F_n\\F_n & F_n + F_{n-1}\end{matrix}\right).$

Сопряженное с золотым сечением число тоже порождает последовательность Фибоначчи, но продолжает её влево от нуля:

$\left(-1/\Phi\right)^n \sim \left(\begin{matrix}F_n + F_{n-1} & -F_n\\-F_n & F_{n-1}\end{matrix}\right).$

Если вычислить их разницу, то получится следующая матрица:

$\Phi^n - \left(-1/\Phi\right)^n\sim \left(\begin{matrix}-F_n & 2F_n\\2F_n & F_n\end{matrix}\right) = F_n\left(\begin{matrix}-1 & 2\\2 & 1\end{matrix}\right).$

Глядите-ка, все соседние числа Фибоначчи, кроме -ного взаимно уничтожились, а матрицу на которую оно умножается, мы уже с вами знаем, это представление $\sqrt 5$ ! Таким образом, мы получаем равенство:

$\Phi^n - \left(-1/\Phi\right)^n = F_n\sqrt 5,$

из которого, очевидно, следует неочевидная формула Бине:

$F_n=\frac{\Phi^n - \left(-1/\Phi\right)^n}{\sqrt 5} = \frac{\left(\frac{1+\sqrt5}{2}\right)^n - \left(\frac{1-\sqrt5}{2}\right)^n}{\sqrt5}.$

Иррациональные корни при вычислении этой формулы исчезают бесследно, поскольку мы работаем в арифметике $ℤ(\Phi)$ , содержащей целые числа и результат не примерно, а точно соответствует целому числу Фибоначчи.

Конечно, эту формулу можно вывести и иначе, не прибегая к матрицам. А отутствие корней в результате несложно объясняется взаимным уничтожением иррациональных слагаемых при раскрытии скобок. Однако матричные представления показывают связь между золотым сечением и числами Фибоначчи настолько очевидно, что грех этим не воспользоваться. Самое же главное: этот подход легко обобщить на любую линейную рекуррентную последовательность, и получать конечные формы для таких рядов в соответствующих расширенных арифметиках!

* * *

Можно было бы тут и закончить рассказ, но я хочу добавить кое-что о том, как этой формулой пользоваться. Давайте закодируем её на языке Julia:

function binet(n) :: Float64
  s = sqrt(5)
  return (((1+s)/2)^n - ((1-s)/2)^n)/s
end

Функция работает, перемалывает числа с плавающей точкой и, действительно, получает целые числа. Но если мы попробуем воспользоваться ею для больших степеней (а именно для них формула Бине должна работать быстрее, чем простая итерация), то выяснится, что использование иррациональных чисел органичивает нас в возможностях.

Что же, выходит, что формула Бине имеет только теоретический интерес? Нет, не зря же мы изучали матричные представления! Они позволяют неявно использовать эту формулу эффективно и без потерь точности.

Возводить число или матрицу в -ную степень можно не просто терпеливо перемножая раз объект сам на себя. Можно воспользоваться известным методом русского крестьянина, который состоит в последовательном применении таких простых тождеств:

$x^{2n}=x^n\cdot x^n\\x^{2n+1}=x\cdot x^{2n}$

Вот как можно использовать их для вычисления -ной степени какого-то числа:

function pow(x,n)
  if n == 0
    return 1
  elseif n == 1
    return x
  elseif iseven(n)
    return pow(x, div(n,2))^2
  else
    return x * pow(x, n-1)
  end
end

А вот так мы возводим в 200-ю степень нашу матрицу, представляющую $\Phi$ :

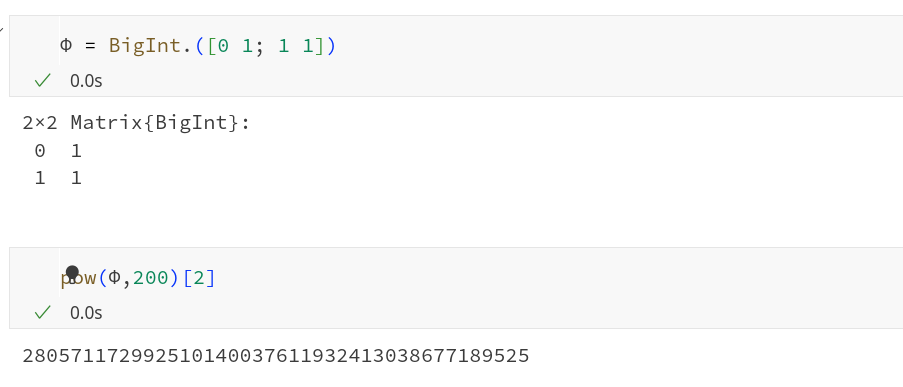
При этом мы не двести раз умножаем одну матрицу на другую, а согласно методу русского крестьянина, используем разложение

$200=2\cdot2\cdot2\cdot(2\cdot2\cdot2\cdot(2+1)+1)$

и значит, выполняем всего 6 матричных умножений (правда с юольшими числами), не теряем точности и можем почувствовать себя крутыми математиками!

В следующей статье мы перейдём к рассмотрению параболических арифметик, познакомимся с дуальными числами и найдём в нашей классификации двумерных арифметик место рациональным дробям. А в качестве практического приложения построим арифметику для вычислений с погрешностями.

Источник

Математическая продлёнка: Изучаем гиперболические числа

Оглавление серии

Двойные числа

Формула Бине

Читайте также

Паблик ВКонтакте

Последние посты