В предыдущих статьях с примерами Jupyter ноутбуков на Google Colab мы наблюдали эффект «танцующих гор» и потом разбирали, как же это возможно. Смотрите Танцующие горы Ирана по данным спутниковой интерферометрии и Спутниковая интерферометрия для танцующих гор Ирана на Google Colab. В статьях рассказано, как можно посчитать движения территории или отдельных объектов путем анализа радарных спутниковых снимков на примере снимков Sentinel-1. Теперь посмотрим, как можно усложнить себе жизнь (однократно), чтобы получать еще более точные результаты автоматически. Вместо ручного выбора референсного изображения построим всевозможные пары изображений и посчитаем для них интерферограммы, чтобы по полученным сериям смещений с заданной их вероятностью (когерентностью) для перекрывающихся интервалов времени найти наиболее вероятную траекторию движения каждого пикселя поверхности за весь период наблюдения. Хотя я стараюсь обходиться без лишних усложнений наподобии записи в матричной форме вычисления среднего значения двух величин (многие работы по интерферометрии делают именно так — демонстрируют матричные уравнения для нахождения среднего значения для смещений, вычисленных раздельно для восходящей и нисходящей орбиты… хоть это формально и правильно, с точки зрения здравого смысла в этом нет никакого смысла), сегодня без линейной алгебры и матриц обойтись нам не удастся, зато я постараюсь объяснить все это в максимально простой и понятной форме.
Введение
Как ранее уже упоминалось, существуют разные техники интерферометрического анализа и наиболее автоматизированные методы являются и наиболее сложными, вплоть до того, что их использования избегают за неимением возможности разобраться в производимых вычислениях. Базовая идея спутниковой дифференциальной интерферометрии достаточно очевидна — вычисляется разница между двумя фазовыми изображениями и пересчитывается в смещение по направлению луча зрения спутника с помощью геометрических построений для радара с известной длиной волны. Если бы не необходимость учета эффекта Допплера, протяженности области съемки (сцены) и используемый способ сканирования местности, эта задача была бы на уровне школьной арифметики. Зато для последующей обработки отдельных интерферограмм и их серий требуются намного более сложные математика и вычисления. Вот про часть этой работы мы и поговорим.
Составление системы уравнений
Развернутая (unwrapped) интерферограмма представляет собой смещения всех пространственно совпадающих пикселов снимков за интервал времени между парой снимков, по которым эта интерферограмма построена. Разумеется, смещение может быть посчитано лишь для тех пикселов, которые представлены на обоих снимках пары. Кроме того, смещение вычисляется с некоторой погрешностью, которая пропорциональна мере когерентности интерферограммы (задается в интервале от нуля до единицы). Более того, даже 100% когерентности не гарантируют 100% аккуратности измерения смещений — типичной проблемой является изменение оптических свойств атмосферы за время между снимками, что приводит к изменению времени на прохождение толщи атмосферы лучом радара, а при вычислениях мы это пересчитываем в ложное смещение поверхности, поскольку эти изменения свойств атмосферы нам не известны. Рассмотрим набор интерферограмм для заданного набора снимков на так называемой диаграмме базовой линии SBAS (SBAS baseline):
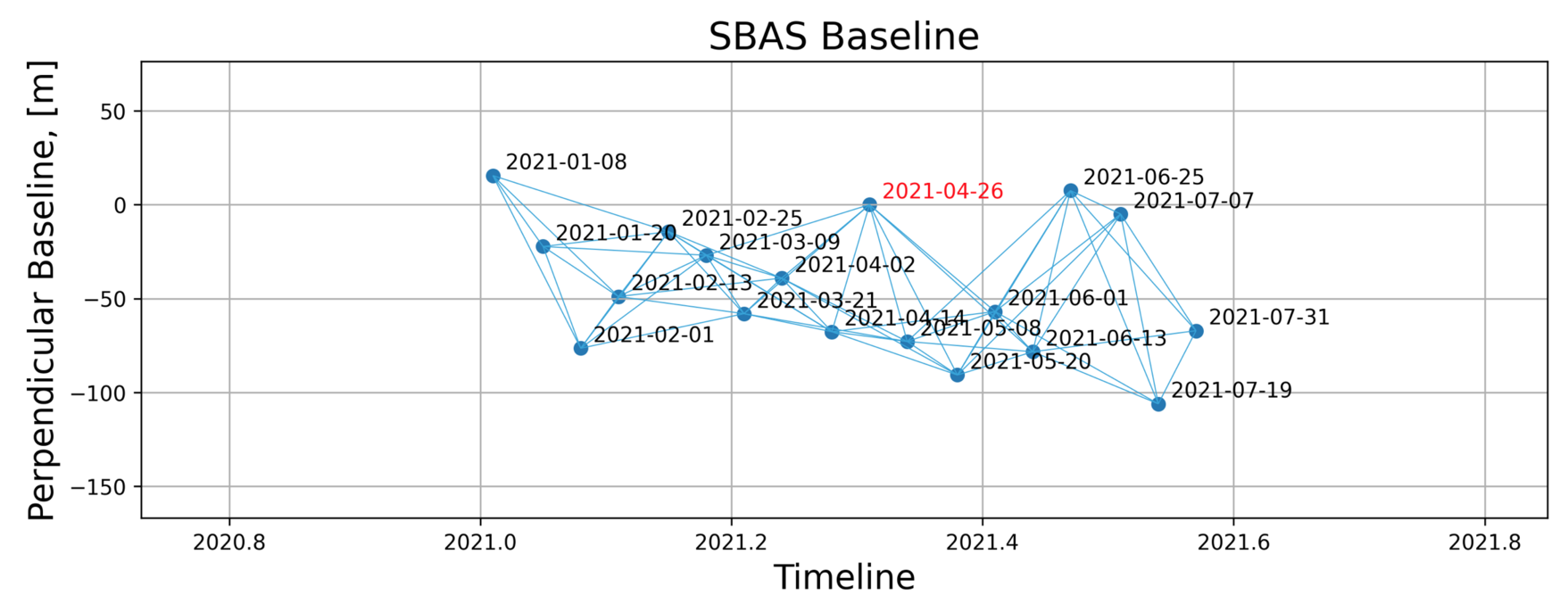
В общем случае для построения SBAS (Small BAseline Subset) диаграммы ограничивается перпендикулярная базовая линия (измеряется по перпендикуляру между положениями спутника в моменты съемки) и временная базовая линия (интервал времени между съемками) для пар снимков для получения потенциально качественных интерферограмм. Для спутников Sentinel-1 перпендикулярную базовую линию можно не ограничивать, так как орбиты этих спутников заданы чрезвычайно точно и, притом, почти совпадают (Ref. tube deviation = ±100 m), см. Sentinel-1 Satellite Description Orbit:
С временным ограничением все интереснее. В самом деле, порой мы можем получить достоверные результаты (высокую когерентность) даже при интервале между снимками порядка года, но только для отдельных пикселов снимков. Таким образом, увеличивая допустимый интервал между снимками, мы значительно увеличиваем количество получаемых интерферограмм, при этом подавляющая часть составляющих их пикселов окажется не пригодными к дальнейшей обработке в силу потери когерентности. Зато так мы получаем возможность проанализировать изменения атмосферы за длительный промежуток времени и внести соответствующие поправки для всех вычисленных смещений. Поскольку изменения атмосферы достаточно плавные относительно пространственной детализации проводимого анализа (масштаб порядка десятка километров), полученные поправки пригодны для значительной территории вокруг каждого пикселя с временной когерентностью в месяцы. В то же время, для определения именно смещений поверхности обычно достаточно ограничиться временным интервалом между снимками 50 дней или около того. В ноутбуке на GitHub я показал примеры вычисления ошибок, вызванных атмосферными эффектами, и как простое исключение соответствующих снимков может значительно улучшить результаты: S1A_Stack_CPGF_T173_TODO.ipynb Отмечу, что здесь вычисления проводятся для интерферограмм целиком, так что этот ноутбук можно запустить и на ресурсах Google Colab, в то время как попиксельные вычисления слишком ресурсоемки.
В статье PyGMTSAR, или спутниковая интерферометрия для всех с примерами Jupyter Python ноутбуков на Google Colab уже рассказывалось, что собой представляет дифференциальная спутниковая интерферометрия (DInSAR), основанная на обработке пар фазовых изображений радарной космической съемки. Мы будем обсуждать исключительно работу со снимками Sentinel-1, которые за счет очень точно известных орбит космических аппаратов позволяют использовать геометрическое выравнивание для получаемых спутниковых снимков.
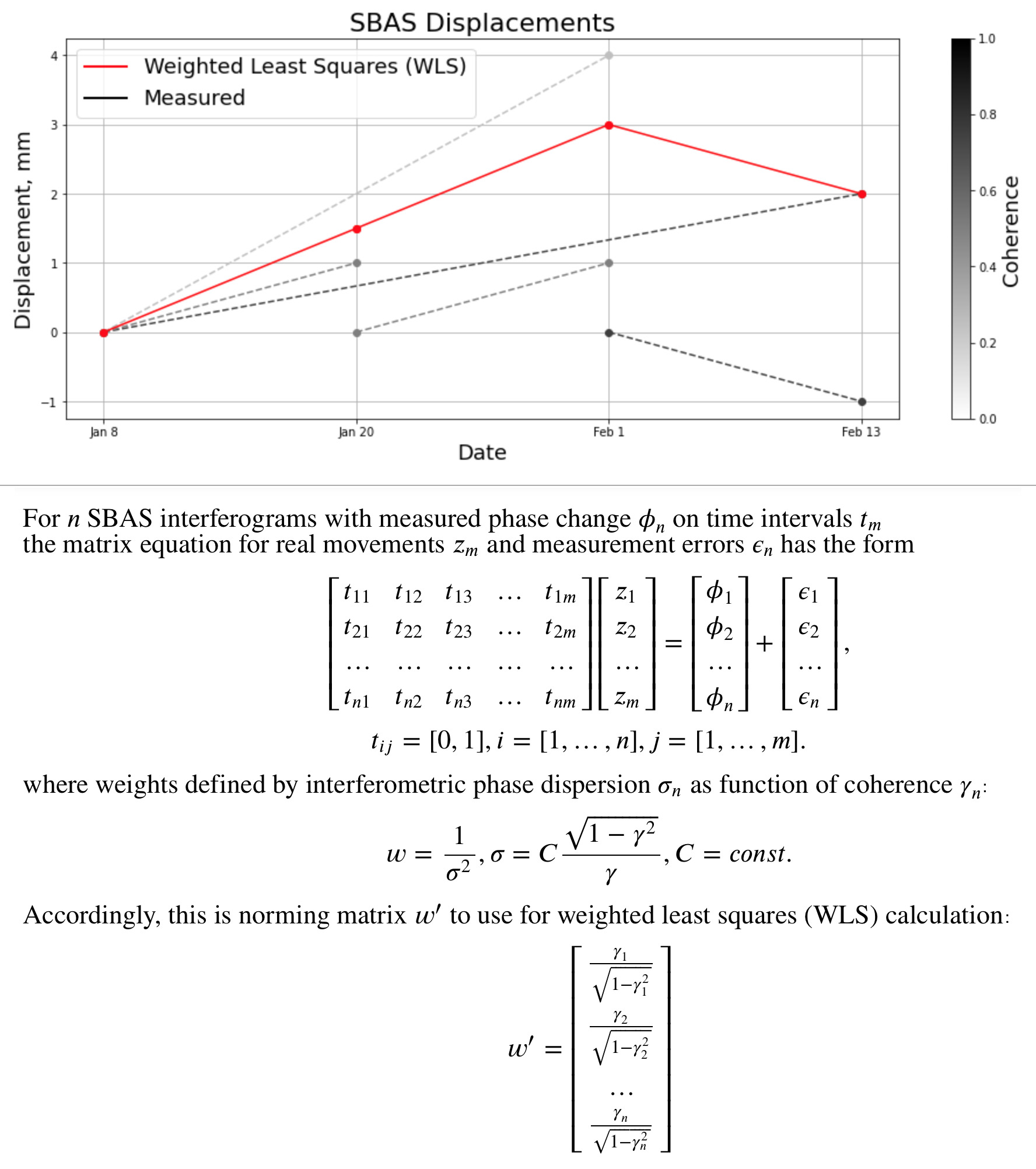
Теперь рассмотрим построение системы уравнений для всех полученных интерферограмм. Выбирая за единицу времени интервал между двумя последовательными снимками (12 дней), для каждого пиксела изучаемой территории мы можем записать серию уравнений, показывающих смещение за серию интервалов времени с заданной достоверностью (определяется когерентностью). Таким образом, когерентность определяет весовой коэффициент каждого уравнения в системе — именно уравнения целиком. Это станет понятнее, если рассмотреть граничный случай при нулевой достоверности (весовом коэффициенте), когда уравнение неразрешимо вовсе и должно быть исключено. При максимальной достоверности уравнение должно учитываться с максимальным весом в решении системы уравнений. Для решения системы уравнений методом наименьших квадратов (LSM) необходимо использовать квадратные корни полученных весов для нормировки системы уравнений (в силу того, что вес каждого уравнения определяет его значимость в решении, а сам метод решения оперирует квадратичными значениями). Ниже приведена получаемая система уравнений и связь дисперсии значений измеренной фазы с интерферометрической когерентностью и с получаемыми весами системы уравнений:

Решение системы уравнений
Как показано выше, решение системы уравнений с весами методом наименьших квадратов (weighted least squares, WLS) может быть также получено нормировкой левой и правой частей системы уравнений на полученные веса и дальнейшим решением модифицированной системы уравнений методом наименьших квадратов (least squares method, LSM). К примеру, подойдет функция linalg.lstsq библиотеки NumPy (конечно, существуют и библиотеки для решения непосредственно WLS).
Для трех интервалов и 5 интерферограмм измеренные значения и решение системы уравнений показаны ниже:
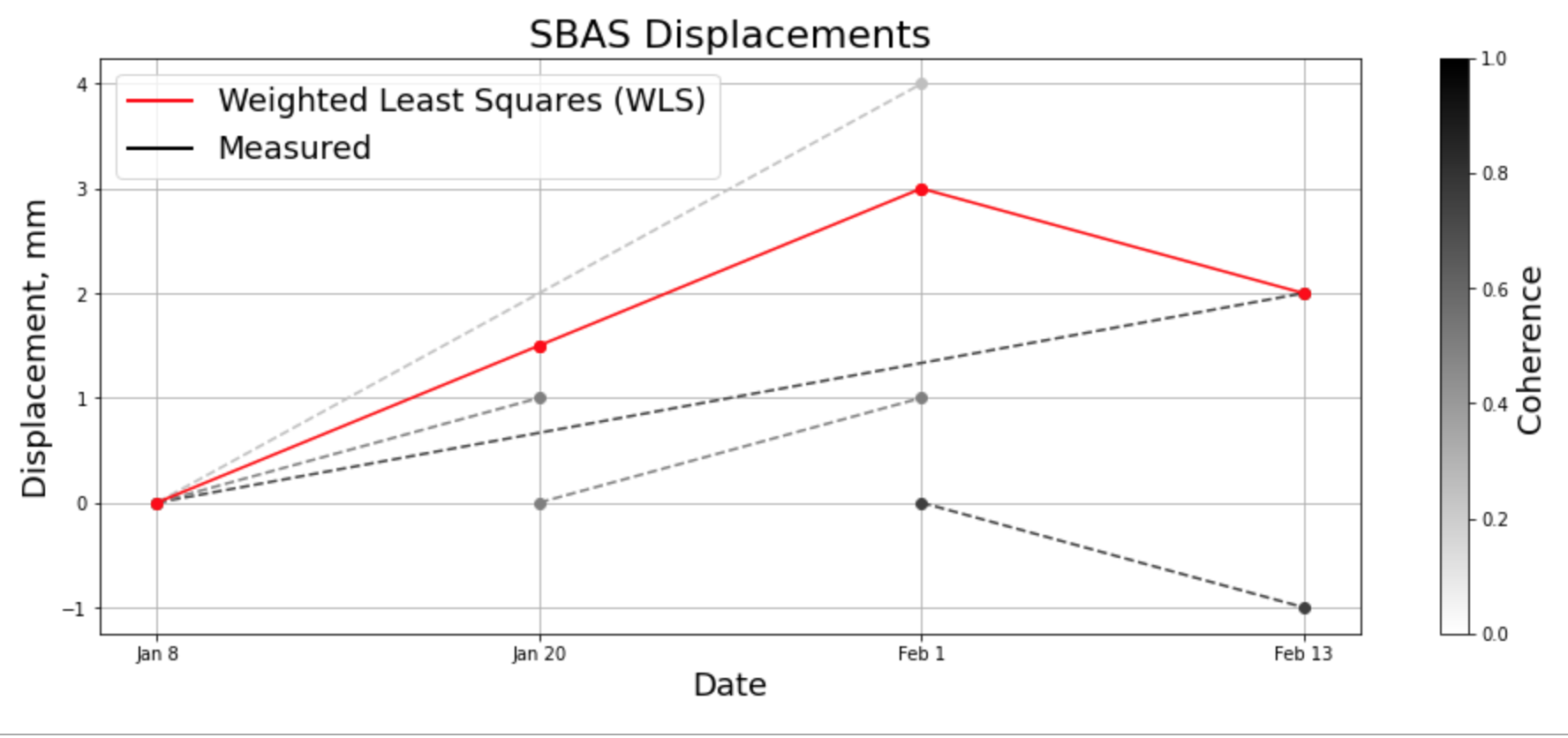
Повторимся, такая система уравнений решается для каждого пиксела отдельно и результат представляет собой смещения пиксела поверхности по направлению луча радара. Для вычисления вертикальной и горизонтальной проекций смещения необходимы как минимум два набора интерферограмм, полученных для двух разных орбит или с разных спутников. Пользуясь исключительно данными с двух орбит Sentinel-1 мы можем определить две проекции (вертикальное и горизонтальное смещение, или вертикальное и смещение север-юг, или вертикальное и смещение восток-запад), но не можем вычислить все три проекции смещения (вертикальное, север-юг и восток-запад). При этом, в силу геометрии орбит спутника Sentinel-1, точность вычисления этих проекций значительно отличается.
Заключение
Эта статья получилась вычислительная, а совсем не геологическая, поэтому я постарался избежать здесь каких-либо геологических подробностей. Если вам интересно практическое применение изложенных подходов — обратитесь к моим предыдущим статьям или ждите следующих 🙂


