Можете представить себе что-нибудь огромнее Вселенной, но в то же время спокойно помещающееся в вашей голове? Что же это такое? Бесконечность! Юджиния Ченг отправляет нас в потрясающее математическое путешествие, чтобы разобраться в самых загадочных математических абстракциях. Почему некоторые числа невозможно сосчитать? Почему бесконечность + 1 не то же самое, что 1+ бесконечность? Мы узнаем о парадоксе «Гранд-отеля», сможем накормить 7 миллиардов человек с помощью шахматной доски, и даже получим бесконечное количество печенек из маленького (конечного) кусочка теста. Всё это позволит понять и полюбить такую странную и загадочную абстрактную математику. Невероятная книга об огромной и бесконечной Вселенной увлекает и интригует, показывая как один маленький математический символ вмещает в себя огромную идею.
ОТРЫВОК. БЕСКОНЕЧНО МАЛОЕ
Один из немногих предметов, которые я могу видеть перед собой прямо сейчас, не имеет ничего общего с математическим анализом — это мой письменный стол. Стол существовал задолго до появления математического анализа, однако данный конкретный стол был сделан на фабрике Икеа, которая совершенно точно использует в своем производстве математический анализ. Я хочу сказать, что изучение бесконечности может казаться чем-то абстрактным и находящимся вне нашего мира, выражаясь буквально и фигурально («фигурно», как любит шутить один из моих друзей), но в конечном итоге оно тоже приводит нас к математическому анализу, который является неотъемлемой частью нашей жизни.
Отправной точкой для всего этого служат размышления об объектах, находящихся «бесконечно близко друг к другу». Когда мы рисуем на компьютере круг или печатаем букву О, они выглядят гладкими и ровными. Но если мы хорошенько приблизим изображения, то они становятся пиксельными. Это буква О в увеличенном масштабе на экране моего компьютера.
Мы видим конечное количество крошечных квадратов, маскирующихся под круг. Мой компьютер старательно подделал круг, он добавил несколько точек серого цвета. Компьютер не может иначе, потому что он способен воспринимать и обрабатывать только отдельные точки в конечном количестве и фиксированном размере.
А как насчет нашего мозга? Смысл математического анализа в том, что наш мозг, в принципе, способен на большее: мы можем воспринимать и обрабатывать бесконечно большие количества объектов, даже если они бесконечно малы. Именно эту тему мы сейчас будем изучать.
Однажды я помогала с математикой в начальной кембриджской школе на Парк-стрит. Я должна была объяснить симметрию двум шестилетним детям. Сначала я попросила их нарисовать линии симметрии на нескольких треугольниках, потом на квадрате, потом на пятиугольнике, потом на шестиграннике. Самым забавным было, когда один из малышей сказал: «Я знаю, что у восьмигранника восемь сторон, потому что слово “восьмигранник” похоже на ОСЬМИНОГ». В конце концов я дала им круг. Один из ребят нарисовал вот такую линию на круге:
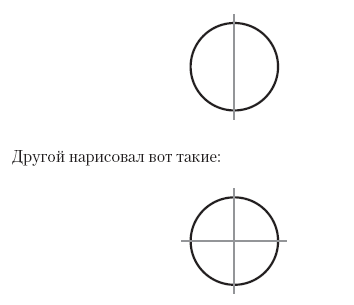
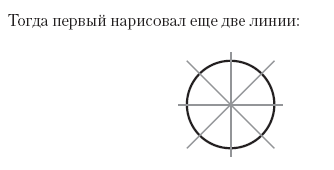
Дальше стало еще веселее. Первый ребенок воскликнул: «Их сотни!», а второй сказал: «Их миллион!», после этого первый заметил: «Ты можешь всю свою жизнь рисовать эти линии и никогда не закончишь!», далее возникла пауза, после которой второй ребенок поднял карандаш, закрасил им весь круг целиком и сказал: «Смотри! Я закончил!»
Я растерялась, но была вынуждена признать, что они оба правы. Вы можете потратить всю свою жизнь на рисование линий симметрии на круге и никогда не закончите, потому что их бесконечное количество. Фактически их несчетно бесконечное количество. Мы можем убедиться в этом. Представьте себе, что мы определили, где проходит линия симметрии, задав угол, который она образует с горизонталью.
Мы можем взять любой угол — от 0 до 180° или в радианах — любой от 0 до π. Если угол будет больше, то линия повторит одну из уже нарисованных:
Возьмем любое действительное число от 0 до 180, причем это не обязательно должно быть целое или рациональное число. Мы уже знаем, что действительных чисел от 0 до 180 несчетно много.
У нас получится несчетно много линий симметрии на круге, однако если вы закрасите весь круг, то вы фактически закрасите их все. Возможно, сейчас вы подумали, что это похоже на жульничество, потому что настоящие линии симметрии должны пересекаться бесконечно много раз в центре круга, а у нас в центре бесконечно много слоев карандаша. Но если мы не будем обращать внимание на центр, а просто попытаемся отметить точки по краю круга, которых касаются линии симметрии, то для этого будет достаточно провести карандашом по краю круга. Нарисуем ли мы таким образом бесконечно большое количество точек? Будет ли в этой линии бесконечно большое количество точек?
Если да, то как далеко друг от друга они расположены? А если их конечное количество, то сколько?
ДЕЛЕНИЕ НА БЕСКОНЕЧНОСТЬ
Если мы делим линию на все большее и большее количество отрезков, то отрезки становятся все меньше и меньше. Сможем ли мы таким образом разделить линию на бесконечно большое количество отрезков? Я хочу сказать, сможем ли мы сделать нечто бесконечно малым, разделив его на бесконечность.
Представьте себе лотерею, в которой могут выпасть все действительные числа. В лототроне будет бесконечное количество шаров, но на каждом из них будет указано определенное конечное число. В этом случае вероятность выигрыша будет довольно странной. Обычно в лотерее в Великобритании выпадают 6 из 59 шаров. Существует примерно 45 миллионов комбинаций, и все эти комбинации одинаково вероятны. Ваш шанс выиграть равен 1: 45 миллионам. Это очень маленькое число (приблизительно 0,00000002), но не 0; хотя мне кажется, оно настолько близко к 0, что фактически может считаться 0. Если вы снова умножите его на общее количество возможных комбинаций (45 миллионов), то получится 1, что совершенно верно, потому что это и будет вероятность выигрыша, если вы купите все лотерейные билеты.
В бесконечной лотерее есть бесконечное количество комбинаций, поэтому ваш шанс выиграть будет равен «1 к бесконечности». Как это выразить с помощью дроби? Ответ не может быть больше 0, потому что если бы он был больше 0, то, умножив его снова на общее количество возможных результатов (бесконечность), мы получим число больше 1. Означает ли это, что вероятность выигрыша равна 0? Но кто-то действительно может выигрывать каждый раз. Вы можете справедливо заметить, что на практике такая лотерея невозможна, но этот ваш довод не отменяет этот парадокс. Тут все точно так же, как с отелем Гильберта: факт, что такой отель не может существовать, не отменяет парадокса.
Мы снова вернулись к одной из первых наших попыток найти бесконечность, утверждая, что
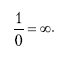
Мы знаем, что такое уравнение порождает противоречие, если мы попытаемся умножить обе его стороны на 0. Но теперь мы хотим сказать, что деление на бесконечность дает 0 или
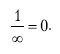
Сейчас мы уже больше знаем о бесконечности и сразу видим, что с этим уравнением что-то не так. Проблема здесь в том, что способ, с помощью которого мы пытались найти бесконечность, а именно — используя бесконечный набор объектов, не подразумевал деления на бесконечность. Правильный математический ответ в данном случае должен быть таким: «Ну что ж, давайте попробуем! Если мы так еще не делали, это не значит, что это невозможно».
Давайте попробуем поступить точно так же, как мы поступили с вычитанием. Снова вернемся к идее того, что все вокруг — это множества объектов. Это как считать на счетных палочках: вы не можете сломать счетную палочку пополам (к великому разочарованию многих детей). Если мы берем множество натуральных чисел, то нельзя частично его сократить.
Помните, когда мы пытались выразить вычитание через бесконечность, мы вспоминали детские рассуждения: 6 – 3 означает «сколько я должен отсчитать назад, чтобы от 3 снова вернуться к 6». Другими словами, мы решали вот такое уравнение: 3 + x = 6.
А теперь давайте возьмем 6: 3. Мы можем рассматривать 6: 3 двумя разными способами.
- Сколько раз по 3 вмещается в 6? Другими словами, сколько раз я должен прибавить 3 к самому себе, чтобы получилось 6? Это все равно что решать вот такое уравнение: 3 × x = 6.
- Какое число вмещается в 6 ровно три раза? Иначе говоря, какое число я могу прибавить к самому себе три раза, чтобы получилось 6? Это все равно что решать вот такое уравнение: х × 3 = 6.
И в том и в другом случае ответ будет 2, потому что эти формулировки не имеют никакого значения, если мы говорим о конечных числах. Но мы уже знаем, что с бесконечностью не все так просто. Например, прибавлять 3 бесконечное количество раз — это не то же самое, что прибавить три раза по бесконечность. То есть 3 × ω ≠ ω × 3.
Давайте зададим себе вопрос: «Сколько раз я должен прибавить 3 к самому себе, чтобы получить ω?» Ответ: ω. Представьте себе, что вы снова превратились в человека, который раздает в очереди отрывные билетики. Люди приходят группами по 3 человека. Сколько групп из 3 человек должно прийти, чтобы у вас кончилась бесконечная пачка билетиков? Ответ: ω. Вы будете просто бесконечно продолжать выдавать по 3 билетика каждой группе.
Если мы посмотрим с другой стороны: «Какое число я могу прибавить к самому себе 3 раза, чтобы получилась ω?», то в этом случае возможного ответа нет. Если вы сложите вместе 3 конечных числа, то ответ всегда будет конечным. Если вы сложите вместе 3 бесконечных числа, каждое из них будет как минимум равно ω (потому что ω — это самая маленькая бесконечность), а все вместе они будут еще больше, это как «бесконечность и еще один день». Мы можем снова рассмотреть это на примере с отрывными билетиками. Если приедет один бесконечно полный автобус, то вы потратите на его пассажиров всю свою бесконечную пачку отрывных билетиков (как минимум). Если после этого приедет еще один бесконечно полный автобус, то вы будете вынуждены взять пачку с билетиками другого цвета.
Оба этих вопроса были попытками «разделить бесконечность на 3», но дали нам разные ответы. Это доказывает, что деление, точно так же, как и умножение, не самый лучший способ решения, если речь идет о бесконечности, даже если это просто деление на маленькое конечное число. Если вместо этого мы попытаемся разделить что-то на бесконечность, то все станет еще хуже. Предположим, что мы хотим сделать следующее:
. Тогда у нас будет два варианта. Первый: сколько раз мы должны прибавить ω к самой себе, чтобы получить 1? Это очевидно невозможно, так как ω — это слишком много. Второй вариант: какое число мы можем прибавить к самому себе ω количество раз, чтобы получить 1? И снова это будет абсолютно невозможно.
Несмотря на все вышесказанное, действительно кажется, что 1, деленная на бесконечность, должна быть равна 0. Может ли это утверждение быть разумным ответом на заданные выше вопросы? Если мы прибавим ω к самой себе 0 раз, мы не получим ничего, так что в этом действии нет никакого смысла. Будет как с 0 бесконечно полных автобусов, для них вам вообще не потребуются отрывные билетики. Что касается второго вопроса: «Можем ли мы прибавить 0 к самому себе ω раз, чтобы получилась 1?», то тут все будет как в случае с 0 людей, которые встают в очередь бесконечное количество раз. Вам снова не понадобятся для них никакие отрывные билетики.
Тут мы могли бы сдаться и сказать: «О’кей, значит, — это не ноль». Или попробовать поступить как математики и сказать: «Все это действительно кажется разумным, может быть, у нас получится придать этому какое-нибудь другое математическое значение, если наши рассуждения не будут основываться на бесконечных наборах?» Одна из задач математики — взять то, что интуитивно кажется верным, и придать ему точное логическое объяснение. Мы не должны так легко сдаваться!
ОБОРОТНАЯ СТОРОНА БЕСКОНЕЧНОСТИ
Возможно, сейчас вы задаете себе вопрос, почему мы не можем просто придумать что-нибудь бесконечно малое и при этом не равное 0, ведь раньше я говорила, что мы можем создавать абстрактные вещи, просто подумав о них. Математики уже пробовали применить такой способ, хоть он и кажется бессмысленным (как и сама идея бесконечности, которая тоже кажется бессмысленной до тех пор, пока не начнешь достаточно интенсивно ее изучать). Это похоже на оборотную сторону бесконечности. Бесконечность больше любого числа, а бесконечно малая величина меньше любого числа. Если вы прибавите бесконечность к самой себе, то получите бесконечность, а если вы прибавите бесконечно малую величину к самой себе, то снова получите бесконечно малую величину. А если вы умножите бесконечность на бесконечно малую величину, то получите 1, как в примере про вероятность выигрыша в лотерею.
Такой подход порождает те же проблемы, что и наша прежняя «выдуманная» бесконечность. Тут нужно действовать с особой аккуратностью или скорее с техническим мастерством, как мы это делали раньше, когда хотели сформулировать четкое определение понятия «бесконечность», но так как проблемы возникают слишком часто, более элегантно будет попробовать их обойти. Если во время прогулки на вашем пути попалась большая грязная лужа, то вы либо наступите на нее, надеясь, что ботинки не промокнут, либо попытаетесь ее обойти. (Конечно, некоторые люди, особенно дети, обожают наступать прямо на центр лужи. В математике такое тоже бывает.)
Вот как можно аккуратно обойти проблему деления на бесконечность. Представьте себе, что вам нужно поделить шоколадный торт на несколько человек. Если вы делите его на двоих, то каждый получает очень много. Если вы делите на троих, то каждый все еще получает много, но уже меньше, чем в первом случае. Если это будут четыре человека, то они получат еще меньше. Чем больше людей, тем меньше торта получает каждый из них. Если количество людей станет по-настоящему огромным, то будет глупо пытаться разделить один несчастный торт на всех. Вы когда-нибудь пробовали разделить торт на сто человек? (Свадебные торты обычно состоят из нескольких ярусов, которые по сути являются отдельными тортами.) А как насчет тысячи человек? А миллиона? В какой-то момент, когда людей станет слишком много, каждый получит настолько маленький кусочек, что это будет фактически ничтожное количество, то есть почти ничего.
Если у нас есть миллион человек и только один торт, то чисто технически каждый получит свой кусочек — вероятно, это будут миллиарды миллиардов молекул торта. Но внешне количество торта будет почти равно 0, и с увеличением количества людей оно будет все больше и больше стремиться к 0. Так мы придали математический смысл идее того, что деление на бесконечность дает 0. На самом деле мы никогда не делим на бесконечность (потому что в этом нет здравого смысла). Давайте лучше вернемся к примеру, о котором мы уже говорили в главе 11, когда нечто стремится к бесконечности. Мы попробовали делить на то, что стремится к бесконечности, и выяснили, что ответ будет тоже стремиться к 0. Возможно, некоторые умники сейчас принесут микроскоп и скажут, что они все же видят на тарелке какое-то количество торта. Но мы всегда можем поделить его еще немного, и торта снова не будет видно. Это не значит, что 1, деленная на бесконечность, равна 0, но эти рассуждения дали нашим интуитивным догадкам математическое объяснение, а с этого и начинался весь современный математический анализ.
ПАРАДОКСЫ ЗЕНОНА
Математический анализ уходит своими корнями в давние времена. Вопросом, как что-то может состоять из бесконечного количества бесконечно малых частей, задавался еще греческий философ Зенон более 2,5 тысячи лет назад. Точно так же, как и Гильберт тысячи лет спустя, Зенон изучал парадоксы, доказывающие, что с бесконечным количеством объектов нужно обращаться очень аккуратно.
Один из парадоксов Зенона похож на размышления ребенка о шоколадном торте: если я съем половину от того, что осталось, потом еще половину от того, что осталось, и так далее, то я буду есть только половину от того, что осталось, и означает ли это, что торт станет бесконечным?
Зенон формулирует этот парадокс так: если вы хотите добраться из пункта А в пункт В, то сначала вы должны преодолеть половину расстояния. Затем вы должны пройти половину оставшегося расстояния. После чего вы должны будете пройти половину нового оставшегося расстояния, и так далее. Вы постоянно проходите только половину оставшегося расстояния.
После каждого этапа всегда остается еще половина расстояния, и всегда можно пройти только половину от того, что осталось. Означает ли это, что вы никогда не доберетесь до места?
Математики очень любят создавать новые понятия из старых, уже изученных. Давайте тоже вернемся к уже пройденной бесконечности натуральных чисел. Мы говорили, что нам нужно преодолеть половину всего расстояния, затем четверть, затем одну восьмую, одну шестнадцатую и так далее «бесконечно». Как мы уже знаем, натуральные числа продолжаются бесконечно. Предположим, что нам нужно пройти одну милю. Тогда можно выделить следующие этапы пути:
У нас есть бесконечное количество n, значит, у нас будет бесконечное количество этапов пути. Мы не можем указать длину каждого этапа, но мы можем записать ее в общем виде: для этого мы применили формулу с переменной n. Но если мы не можем записать длину каждого этапа, то можем ли мы закончить каждый из них? Ответ должен быть: да, потому что заканчивать путь — это вполне нормально для каждого из нас. Обычно мы заканчиваем наши пути, даже самые короткие, причем делаем это каждый день. (Я не каждый день выхожу из дома, однако иногда умудряюсь несколько раз за час сходить к холодильнику.)
В аналогичном парадоксе, тоже сформулированном Зеноном, речь идет об Ахиллесе и черепахе, которые бегут наперегонки из точки А в точку В. Черепахе разрешается начать движение первой, скажем, в точке А1, но она движется очень медленно, ведь она же черепаха! А Ахиллес должен сначала добежать до места черепашьего старта. За это время черепаха уходит немного дальше, допустим, до точки А2. Теперь Ахиллес должен добраться до этой точки; пока он это делает, черепаха проходит еще немного, например до точки А3. Сейчас Ахиллес должен добраться уже до А3, и за это время черепаха доползает до точки А4. Каждый раз, когда Ахиллес добегает до того места, где черепаха была в момент, когда мы последний раз проверяли статус гонки, черепаха уходит еще немного дальше. Означает ли это, что черепаха победит в забеге?
Оба этих парадокса строятся на вполне логичных доказательствах, которые приводят к абсурдному выводу. Обычно мы вполне способны добраться до места назначения. И очевидно, что если Усейн Болт побежит наперегонки с черепахой, то выиграет гонку. Смысл этих парадоксов заключается не в том, чтобы обнаружить ошибки в нашей реальности, а в том, чтобы обнаружить ошибки в логике наших аргументов.
Этот парадокс отличается от парадокса про отель Гильберта, который хотя и может быть заполненным, еще способен размещать вновь прибывших постояльцев. В нем вывод звучит абсурдно, потому что наши интуитивные представления о бесконечных отелях не совсем правильные.
Такие парадоксы, как парадокс про отель Гильберта, называются истинными парадоксами; в них веские доводы приводят к выводу, который кажется противоречивым, но на самом деле таковым не является. Такие парадоксы, как парадокс Зенона, называются ложными парадоксами, в них противоречивый вывод получается из аргументов, которые кажутся верными, но не являются таковыми в действительности.
И в том и в другом случае суть парадокса в том, чтобы продемонстрировать странности, которые возникают, когда мы начинаем думать о бесконечности: в парадоксе про отель Гильберта мы имеем дело с бесконечно большими объектами, а в парадоксах Зенона — с бесконечно малыми. В парадоксе про отель Гильберта перед нами встает проблема бесконечного возникновения объектов, чего в реальной жизни не бывает, будь то туфли, носки, отрывные билетики или номера в отеле. А в парадоксах Зенона нам начинает казаться, что объекты возникают бесконечно, если мы допускаем оговорку, что при этом они становятся бесконечно малыми. Они не могут быть бесконечно малыми, потому что мы не знаем, что это означает на самом деле. Но они могут становиться бесконечно малыми. Мы каждый день сталкиваемся с бесконечными множествами объектов, порой даже не зная об этом и не имея необходимости об этом знать.
БЕСКОНЕЧНО БОЛЬШОЕ КОЛИЧЕСТВО БЕСКОНЕЧНО МАЛЫХ ОБЪЕКТОВ
В парадоксе о пути из точки А в точку В нам удалось добраться до места назначения, а это значит, что мы смогли преодолеть бесконечное количество отрезков пути. Однако это возможно только потому, что эти отрезки становились все меньше и меньше и время, которое мы затрачивали на каждый отрезок, тоже становилось все меньше и меньше. Причем это происходило в реальном мире, а не в фантастическом мире Гильберта, где у нас каким-то образом появляется достаточно времени для того, чтобы заполнить бесконечное количество номеров отеля или выдать бесконечное количество отрывных билетиков. В реальной жизни мы каждый день можем делать бесконечное количество вещей, но только в том случае, если время, которое мы тратим на каждую из них, будет бесконечно малым.
Представьте себе, например, что вам нужно пройти милю до железнодорожной станции. Допустим, вы идете с постоянной скоростью 4 мили в час. Значит, это должно занять у вас 15 минут. Но о чем говорит парадокс Зенона?
- Сначала вы должны пройти первую половину мили, что займет у вас 7,5 минуты.
- Затем вы должны будете пройти следующую четверть мили, что займет у вас 3,75 минуты.
- Далее вы должны будете пройти одну восьмую часть мили, что займет у вас 1,875 минуты.
- После этого вы должны будете пройти одну шестнадцатую часть мили, что займет у вас 0,9375 минуты.
- …
Вы должны пройти все эти бесконечно уменьшающиеся отрезки пути, но у вас уходит на это бесконечно уменьшающееся количество времени. Сколько вы пройдете таких маленьких отрезков, пока будете добираться до железнодорожной станции? Ответ: бесконечно много; если вы будете останавливаться после каждого конечного отрезка пути, то всегда будет оставаться еще немного.
Очевидно, что это совершенно абсурдный способ считать, сколько времени потребуется, чтобы добраться до железнодорожной станции, особенно потому, что в определенный момент крошечное расстояние, которое вам еще осталось пройти, станет меньше ступни. Однако для нас это важный мысленный эксперимент, который демонстрирует следующее: нам кажется, что можно сложить бесконечно большое количество объектов и получить конечный результат, если эти объекты постоянно становятся все меньше и меньше. В реальном мире мы не сможем выдать бесконечное количество отрывных билетиков, потому что все отрывные билетики имеют одинаковый размер. Но даже если бы они становились все меньше и меньше, нам все равно требовался бы определенный и отдельный отрезок времени, чтобы выдать каждый билетик, поэтому мы действительно не можем этого сделать. Мы не можем откусывать один шоколадный торт бесконечно, даже если наши «откусы» становятся бесконечно малыми, потому что расстояние до нашего рта всегда будет одинаковым. (Хотя мы можем одновременно сокращать расстояние до рта, но в итоге все закончится подбородком на тарелке с тортом.)
Здесь есть две загадки. В каких случаях имеет смысл складывать бесконечно большое количество крошечных объектов? И как в таких случаях мы сможем посчитать ответ? Этот вопрос, мучивший математиков тысячи лет, был наконец-то разрешен в XIX веке с появлением математического анализа. Мы вернемся к нему в следующей главе.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Математика
Источник
