Этот разумный, но, на первый взгляд, парадоксальный вопрос просто неправильно задан. Это последствия того, что вы представляли себе совсем не то. Я попытаюсь исправить ход ваших мыслей.
Вернёмся назад и посмотрим на рис. 3 из статьи про одномерные миры. Нужную нам часть этого рисунка я воспроизвёл на рис. 1 в этой статье. Обратите внимание на два совершенно разных представления эоловой линии (измерения возможных направлений ветра, куда входят такие направления, как север, юго-восток, запад-север-запад, и т.п.). Одно из представлений — отрезок прямой, левый конец которого совпадает с правым. Другое — петля на плоскости. Секундочку, скажете вы — они выглядят по-разному. Петля окружает определённую область, у неё есть внутренняя и наружная часть. У отрезка такого нет. Так как же они могут изображать одно и то же?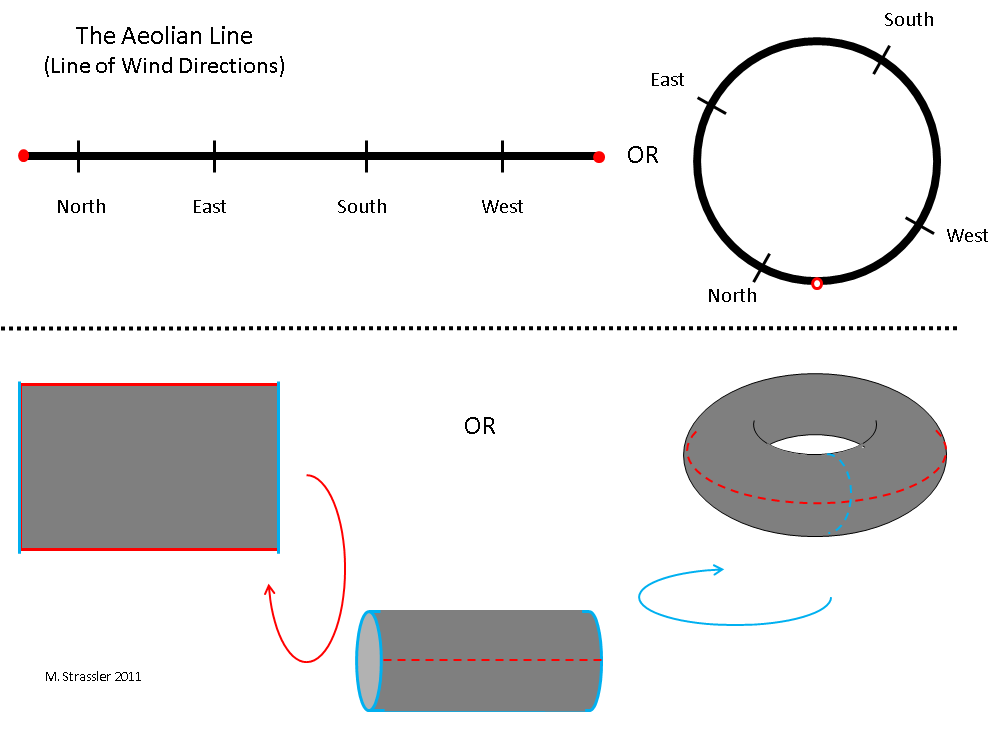
Рис. 1
Да, это, действительно, крайне важный вопрос, и ответ на него необходим для понимания пространств. Два изображения — петля и отрезок с двумя совпадающими концами — действительно представляют одну и ту же одномерную эолову линию. Область, окружённая петлёй — это лишь свойство выбранного нами представления, а не свойство самой эоловой линии! Мы не должны путать свойства картинок, используемых нами для визуализации, со свойствами пространств! Это легко сделать, но очень важно этого не делать.
В качестве другого примера показан пончик (тор), у которого вроде бы есть внутренняя и наружная части. Но это не так. Точно так же, как круг можно представить отрезком с левым концом, совпадающим с правым, так и тор можно представить в виде прямоугольника, у которого верхняя сторона совпадает с нижней, а левая — с правой.
Чтобы проверить это, возьмите лист бумаги. Соедините верхний край с нижним. У вас получится цилиндр. Используйте воображение, чтобы согнуть правый и левый его концы так, чтобы они соприкоснулись — и вы сразу увидите, что должен получиться тор.
У прямоугольника с совпадающими сторонами нет никакого «внутри» и «снаружи», поэтому у цилиндра или тора этого тоже нет. Иначе говоря, свойства пространства можно изучить, если вы путешествуете внутри него. Чтобы увидеть, что у круга есть внутренность и наружная часть, вам нужно его пересечь: но если ваш круг — это эолова линия, то это невозможно. Ветер нельзя попросить пересечь круг с севера на юго-восток. Он может перемещаться только по кругу, через восток или через запад. Эоловой линии присуща только сама эта линия!
Точно так же нельзя попросить канатоходца с рис. 6 статьи про одномерные миры перейти с одной части кругового каната на другую. Единственным безопасным вариантом для его движения будет пройти по кругу. Поэтому ветер или канатоходец не может выяснить, есть ли или нет у круга внутренняя и наружная части.
Эта концепция крайне важна для понимания расширения Вселенной. Если вы принадлежите к большинству, вы, наверное, размышляли (как делал я в молодости): «Во что же она расширяется?» Задавая этот вопрос, вы совершали ту же ошибку, что относится к кругу: вы путали нечто расширяющееся с представлением чего-то расширяющегося.
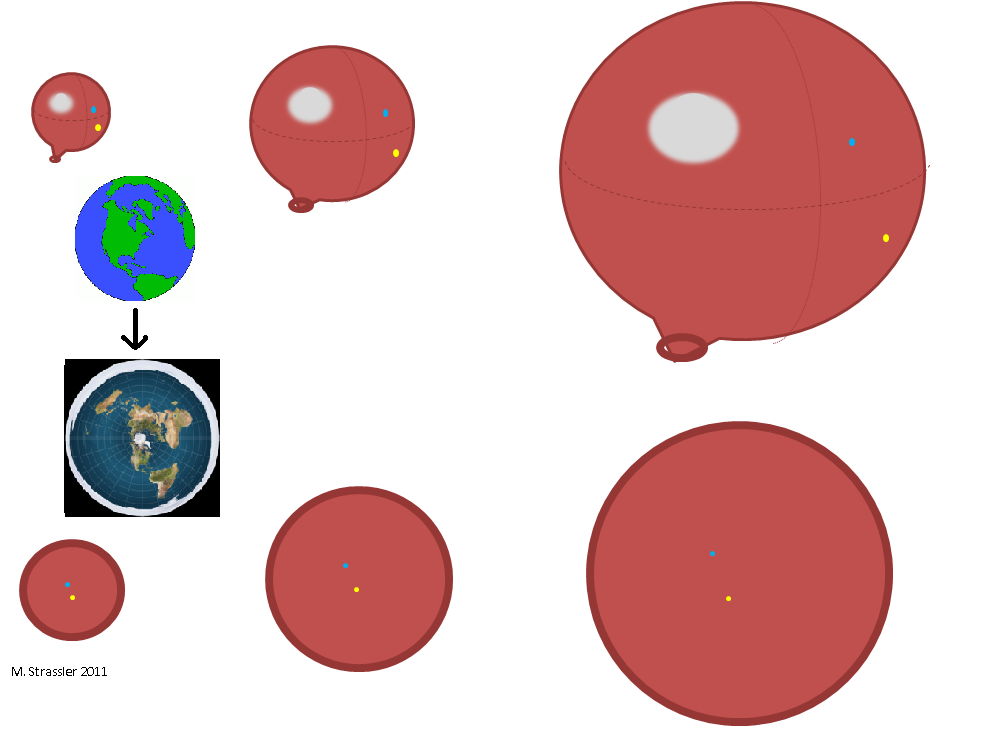
Рис. 2
К примеру, можно представить себе расширяющийся шар. Шар выглядит для нас так, будто он расширяется в более крупное трёхмерное пространство, в котором он находится. Но если бы вы были муравьём на шаре, вы не знали бы ничего по поводу каких-то там внутренней и наружной частей; вы бы только знали, что пространство, по которому вы способны передвигаться, стало больше. Вы бы даже могли, будучи муравьиным картографом, представить это пространство в виде диска, чьи края сведены в одну точку (например, в ту точку, через которую шарик надувают). Вы бы не думали про «внутри» и «снаружи», вы бы знали только, что расстояние между жёлтой и голубой точками (и между любой парой точек на шаре) растёт.
Ещё одна двумерная поверхность — это поверхность самой Земли. Допустим, что как-то утром вы проснулись, а поверхность Земли удвоилась. Вам не было бы известно, изменился ли вид Земли для наблюдателя из космоса, или вырос ли диаметр Земли. Вам только было бы известно, что поездка на работу или за продуктами занимает дольше, чем раньше.
То, что внутренняя или внешняя часть шарика — это свойство представления расширяющегося пространства, а не самого пространства, более очевидно на примере с бесконечной плоскостью. Бесконечная плоскость вполне может расширяться, хотя она не расширяется ни во что. Она заполняет то же самое пространство после расширения, как и до него, просто расстояния между объектами в пространстве (к примеру, между показанными на рисунке точками) вырастают. Плоскость по сути растёт в размерах, но она не находится внутри более крупного пространства, и поэтому, очевидно, не может расширяться в это более крупное пространство. Она просто может расширяться, и всё.
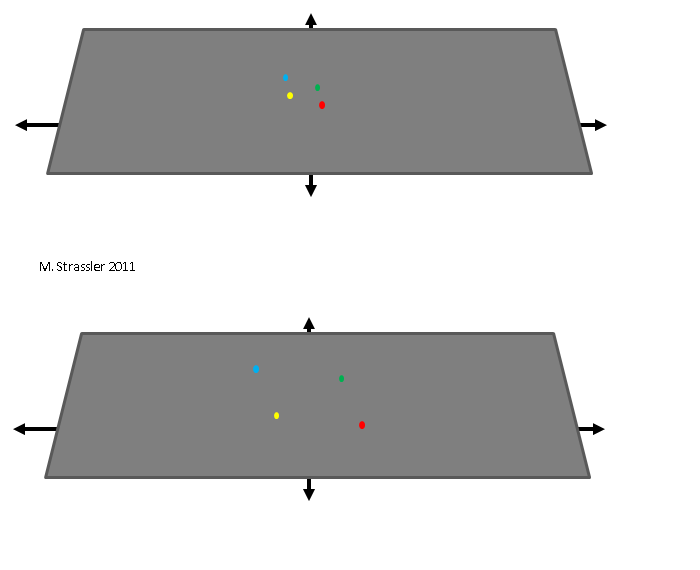
Рис. 3
Так вот и со Вселенной. Как только что описанная плоскость, пространство Вселенной просто расширяется. Снаружи это увидеть нельзя, никакого «снаружи» просто нет. Но расширение Вселенной можно определить, и находясь на самой плоскости: расстояние между любыми крупными объектами Вселенной (в частности, между галактиками, огромными вселенскими звёздными городами) растёт и растёт по мере расширения Вселенной. Со временем путешествие из одной галактики в другую будет занимать всё больше и больше времени. Именно это и сделал Большой взрыв: взял небольшие участки пространства и превратил их в огромные. Это был не взрыв, это не было похоже на взрыв бомбы. Это расширение самого пространства.
Источник


