
Большие числа != большим числам.
Число 100 большое? Зависит от ситуации. Сравниваем ли мы его с 0,001, или с 100000? Как и многое в жизни, понятие «большой» относительно.
В этом посте мы объясним, насколько большим должно быть «большое» и докажем, что вы, скорее всего, ошибаетесь насчёт закона больших чисел.
Закон больших чисел (ЗБЧ)
Проведём эксперимент: будем бросать кубик, как делали это на уроках знакомства с вероятностями. Будем продолжать совершать тысячи бросков, каждый раз вычисляя среднее выпавшее значение.
(Следует помнить, что среднее ожидаемое значение броска кубика равно (1+2+3+4+5+6)/6 = 3,5.)
Вот график первых десяти бросков.
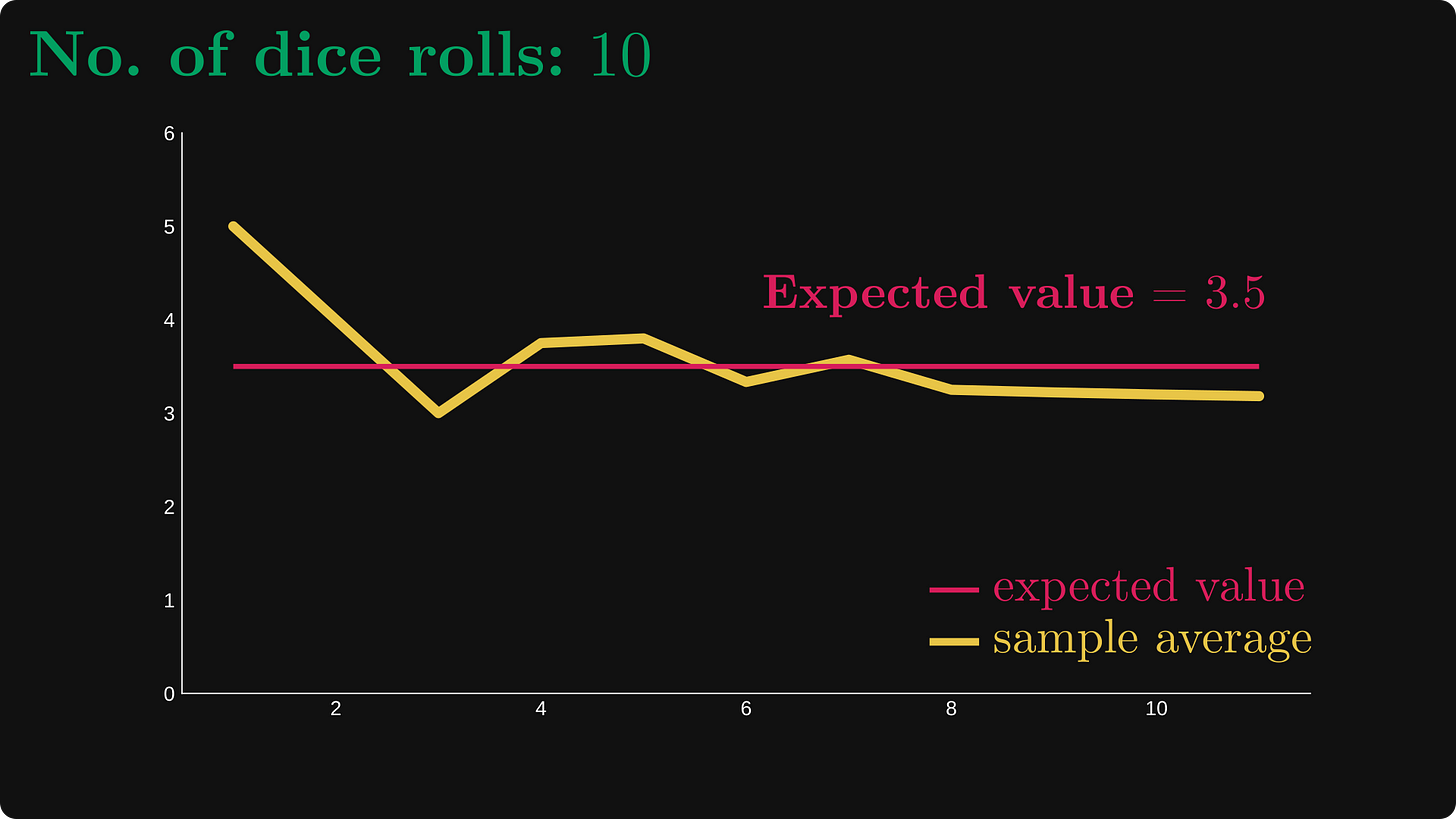
Сначала мы выбросили 5, затем 1, и так далее.
Теперь давайте проверим, что произойдёт, если увеличить количество экспериментов до 100 и 1000:


Чем «больше» становится число, тем ближе средние значения выборки к истинному ожидаемому значению. Закон больших чисел говорит именно об этом: среднее значение выборки сходится к среднему ожидаемому значению.
Если точнее, существует две версии ЗБЧ: слабая и сильная.
Слабый закон постулирует следующее.

Иными словами, вероятность того, что среднее значение выборки X̅ₙ находящееся на любом расстоянии от ожидаемого значения μ, сходится к нулю с увеличением количества выборок (n). (Подробнее мы рассмотрим это ниже.)
Похоже, n = 1000 достаточно «большое» для эксперимента с кубиком. А как насчёт других ситуаций?
Давайте рассмотрим другой пример! Вот этот лотерейный билет из Техаса со стираемыми полями.

На официальной веб-странице написано следующее:
-
Выигрыши на общую сумму $829 миллионов!
-
Сумма выигрыша от $150!
-
Шанс выиграть $20 000 000
-
Билет стоит всего $100!
Звучит прекрасно, но мы знаем математику достаточно хорошо, чтобы не обманываться этими числами. Если покопаться, мы сможем найти вероятность выигрыша. Вот таблица выигрышей с официального сайта:
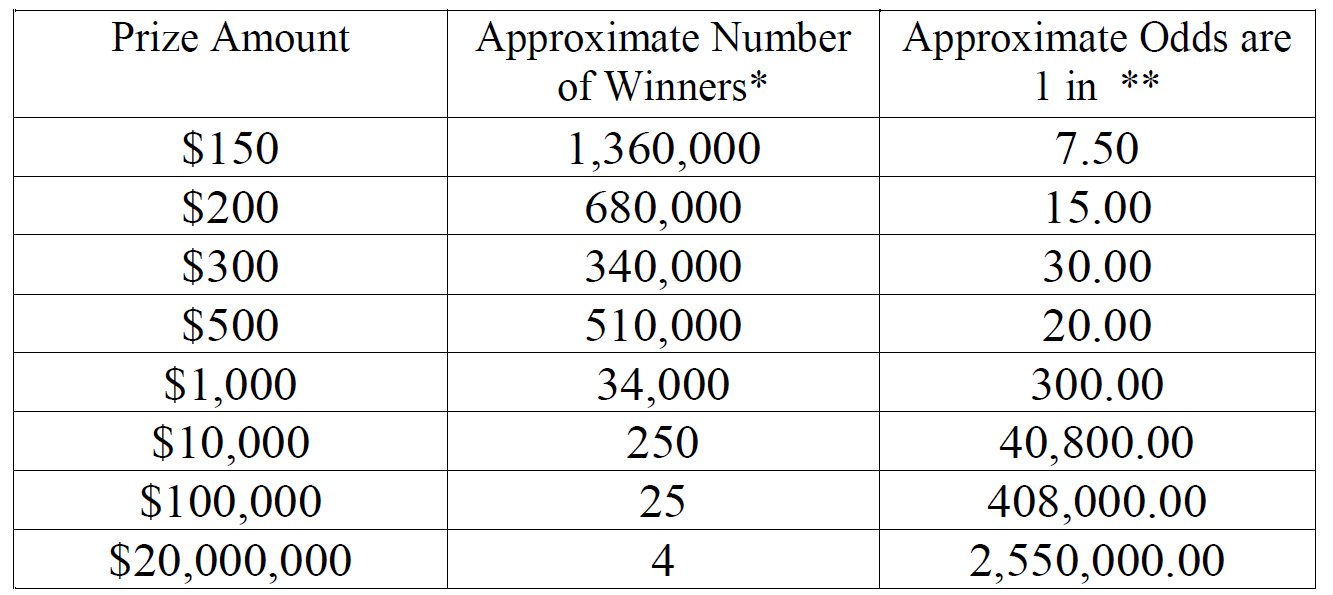
Зная это, мы можем с лёгкостью вычислить наши шансы и ожидаемые значения:
-
шанс что-то выиграть составляет 26,34%,
-
а ожидаемая выплата составляет $75,28958 на билет. (Не учитывая $100 за участие.)
Похоже, билет за $100 покупать не стоит, потому что ожидаемое значение равно всего примерно $75,3.
А теперь давайте проведём эксперимент, похожий на эксперимент с кубиком. Мы (гипотетически) покупаем всё больше и больше билетов, параллельно вычисляя средние выигрыши. Чем больше билетов мы купим, тем ближе будем к ожидаемому значению (примерно $75).
С первыми десятью билетами нам не очень повезло.

Но давайте купим ещё девяносто! С сотней билетов мы приблизились к ожидаемому, но на долгую перспективу нам нужен сглаженный график рядом с красной линией.

Давайте совершим шаг побольше: увеличим n до 10000.
Теперь у нас получилась плавная линия, но это совсем не то, что мы ожидали! Она находится примерно рядом с $67, а не с ожидаемым значением.

Давайте пойдём дальше. С одним миллионом билетов снова происходит что-то странное: нам начинает везти и выигрыши превышают среднее. Теперь мы отдалились ещё больше!
Похоже, 1000000 — это всё ещё не «большое» число!

Пойдём дальше! При десяти миллионах билетов у нас получается множество крупных выигрышей, которые поднимают среднее вверх, но эффект становится всё меньше и меньше. Мы медленно, но верно приближаемся к ожидаемому значению.
Теперь мы наконец получили ожидаемую плавную линию, находящуюся рядом с истинным средним.

В первом эксперименте мы смогли продемонстрировать закон больших чисел на тысяче бросков, но во втором не хватает даже миллиона.
Большие числа != большим числам.
Как же объяснить странности, произошедшие во втором эксперименте?
Дисперсия и скорость сходимости
Давайте приглядимся к слабому закону больших чисел!
По сути, вероятность P(|X̅ₙ — μ| > ε) — это показатель расстояния между средним значением выборки до истинного среднего (то есть ожидаемого значения) в вероятностном смысле.
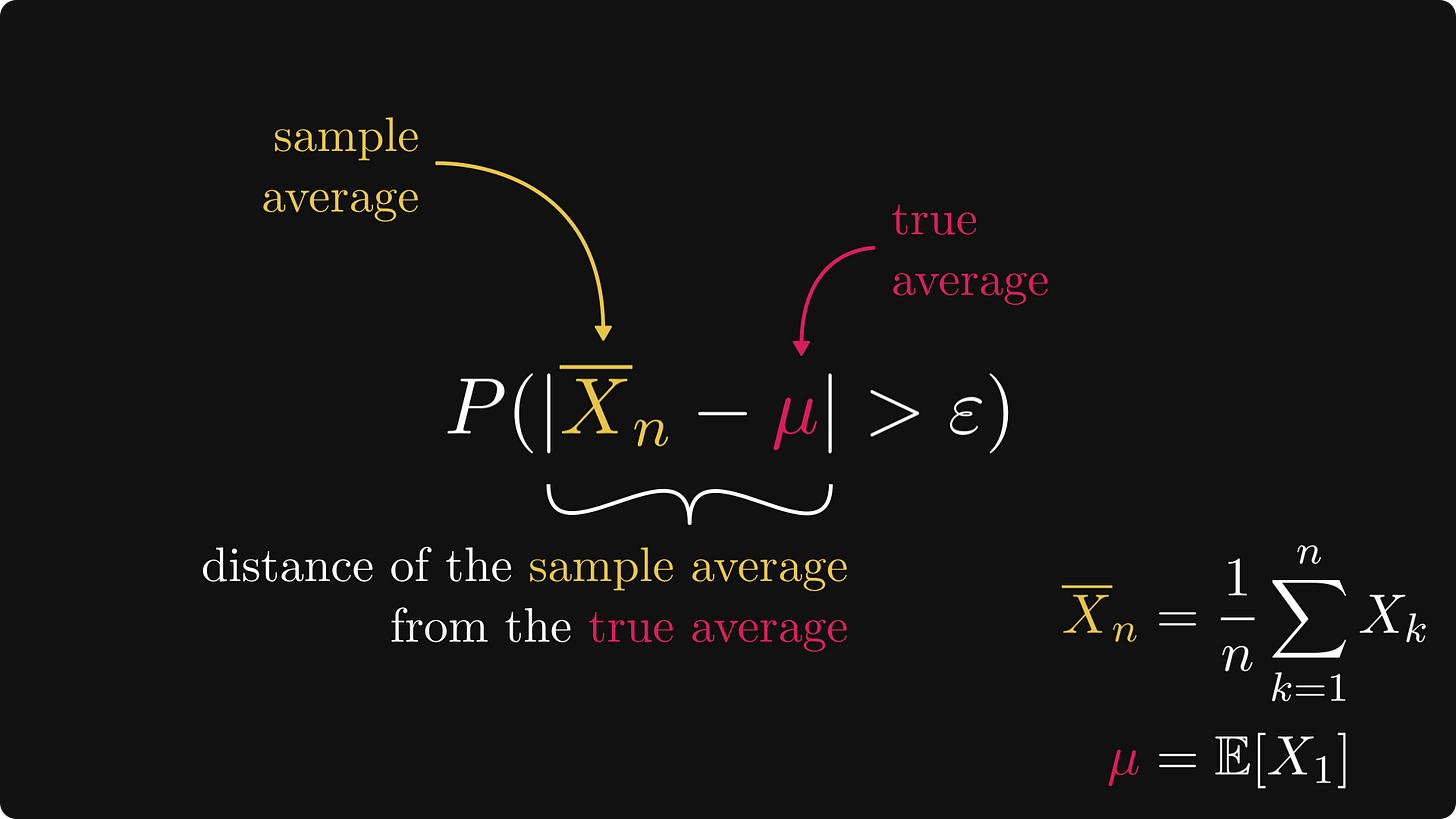
Чем меньше ε, тем больше вероятностное расстояние. В математической записи верно следующее:

Слабый закон больших чисел гласит:

то есть, вероятностное расстояние становится маленьким, как мы и хотели.
Грубо говоря, это означает, что среднее значение выборки равно истинному среднему плюс распределение, которое становится всё более и более концентрированным в области нуля. Иными словами, мы имеем:
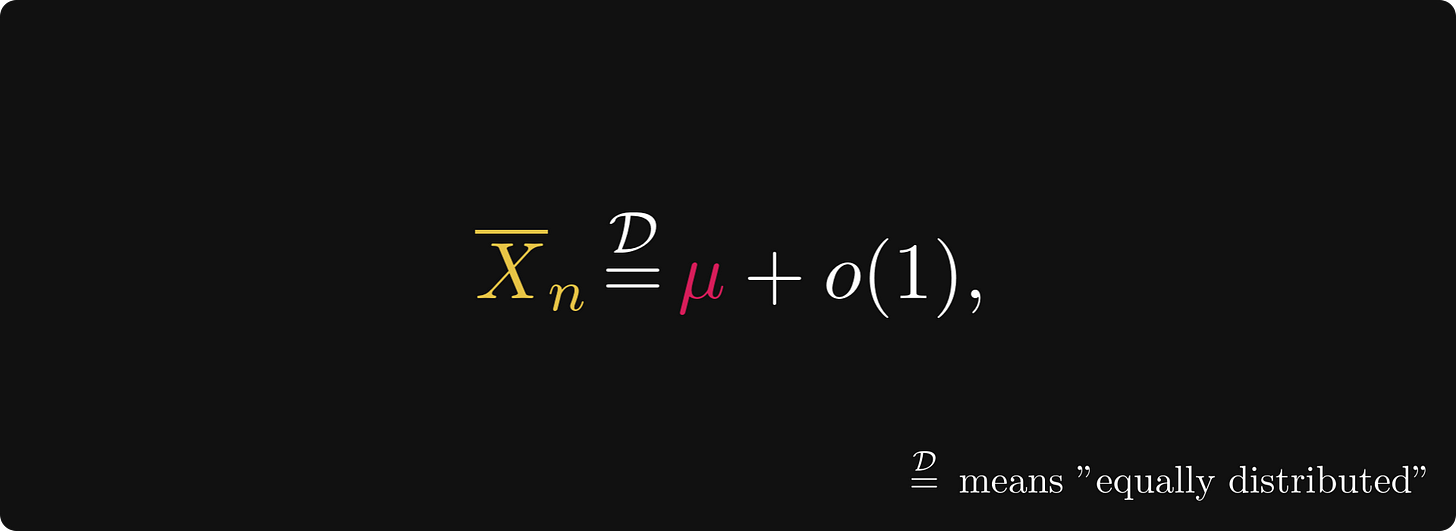
асимптотическое расширение в смысле распределения. Член o(1) обозначает распределение, которое с ростом n aстановится всё более концентрированным в области нуля. Возможно, вы знакомы с обозначениями большого и малого «O»; это тоже самое, но с распределениями вероятности.
Объясняет ли слабый закон больших чисел и асимптотическое расширение происходящее с нашими лотерейными билетами; то есть, почему нам нужно десять миллионов выборок, чтобы достаточно приблизиться к истинному среднему?
Краткий и жёсткий ответ: нет.
Нам нужно асимптотическое расширение большего размера. Нашим инструментом для этого будет центральная предельная теорема — один из самых известных результатов в теории вероятностей, формализующий понимание того, почему средние значения выборки напоминают гауссовы распределения.
Центральная предельная теорема
Давайте сразу нырнём с головой и перейдём непосредственно к центральной предельной теореме (central limit theorem, CLT). Она гласит, что с точки зрения распределения масштабированные на √n средние центрированные значения выборок сходятся к стандартному нормальному распределению. (Термин «центрированные» означает, что мы вычитаем ожидаемое значение.)

Нужно подчеркнуть, что эта сходимость справедлива в случае распределений. Это просто иной способ сказать, что кумулятивные функции распределения являются сходящимися поточечно. (Знаю, сходимость в теории вероятностей — это довольно запутанная тема.)
Давайте развернём это: для асимптотического расширения закон больших чисел и центральная предельная теорема подразумевают, что

то есть среднее значение выборки равно сумме 1) ожидаемого значения μ, 2) масштабированного нормального распределения и 3) распределения, сводящегося к нулю быстрее, чем 1/√n.
То есть для нашего асимптотического расширения мы имеем

Это можно переписать в упрощённом виде, если объединить константы в нормальное распределение. А именно, мы получаем

и это значит, что наше асимптотическое расширение принимает вид

Иными словами, при больших n среднее значение выборки приблизительно равно нормальному распределению с дисперсией σ²/n. Чем больше n, тем меньше дисперсия; чем меньше дисперсия, тем сильнее нормальное распределение концентрируется рядом с ожидаемым значением μ.
И это даёт ответ на наш вопрос: каким должно быть зловещее число в законе больших чисел? Это зависит от дисперсии нашего распределения!
Из нашего асимптотического расширения можно понять, что если дисперсия в 10 больше, то чтобы среднее было так же близко к изначальному, нам нужно приблизительно в десять раз больше выборок. Это происходит из-за члена σ²/n, где σ² обозначает дисперсию нашей выборки X₁, X₂, …, Xₙ, а n обозначает количество выборок.
Давайте вернёмся к броскам кубиков и лотерее. Дисперсия броска кубика составляет 35/12 ≈ 2,916, а дисперсия техасской лотереи — приблизительно 157 000 000. Это в пятьдесят миллионов больше. То есть в среднем нужна выборка в пятьдесят миллионов раз больше, чтобы среднее значение выборки было столь же близко к истинному среднему, как и в случае кубиков.
Также важно заметить, что поскольку закон больших чисел — это вероятностная формулировка, утверждения типа «нам нужно в пятьдесят миллионов раз больше образцов» должны пониматься вероятностно. Если нам повезёт, среднее значение выборки может быть очень близко к истинному среднему же через несколько тысяч образцов.
Заключение
Закон больших чисел часто понимают неверно.
Мы используем его достаточно часто, но он имеет важную тонкость. Хотя среднее значение выборки сходится (почти гарантированно) к ожидаемому значению, скорость сходимости зависит от дисперсии выборки. Чем больше дисперсия, тем медленнее сходимость.
И для множества практических применений это оказывается плохим известием. Например, поэтому сходимость метода Монте-Карло медленна. В реальной ситуации, например, в азартных играх, у вас даже могут закончиться деньги, прежде чем вы начнёте выигрывать. (Впрочем, у большинства игр в казино ожидаемое значение отрицательно, поэтому в длительной перспективе вы всегда будете проигрывать.)
Какой же можно сделать из этого вывод? Применяя закон больших чисел, всегда учитывайте скорость сходимости.


