Забегая вперед скажу, что всё, что касается программирования в Space Engineer, будет в следующей статье. В этой я расскажу про обратную кинематику и покажу прототип на HTML Canvas в котором я занимался отладкой алгоритмов.
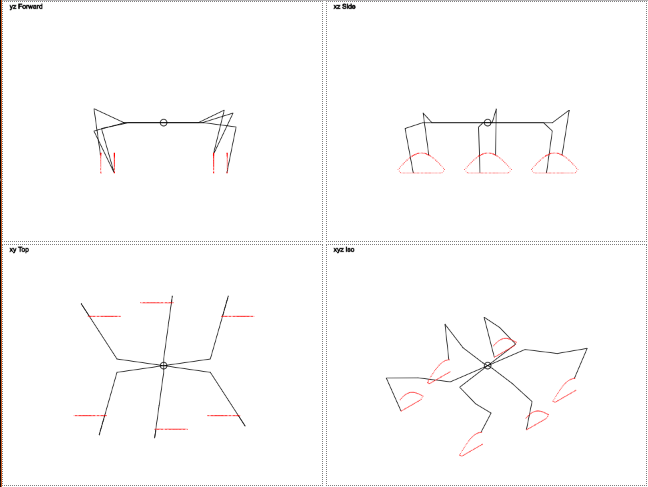
Предыстория и постановка задачи.
Изначально было построено сочлененное шасси, а затем на нем копательный агрегат. Такая конфигурация обеспечивала контакт всх колес с поверхностью на больших неровностях, в том числе и при скручивании.

Вроде такого
Но я столкнулся с невозожностью его точно разместить на месторождении, так-как колеса часто соскальзывали вниз (проблема физики — большинство блоков (в том числе и колеса) имеют слишком малый коэффициент трения). Колесная платформа с цельноповоротными колесными модулями оказалась слишком громоздкой и страдала от периодических physics explosion. В результате было решено строить шагающего робота — а именно — гексапод, как самую стабильную шагаюшую платфрому.
С чего начнет строить гексапод нормальный человек? Наверное зайдет в игру и начнет строить тело робота с конечностями, а потом думать как это всё оживлять. Но это не наш метод (ц)
Я начал с теории
Для строения ноги была выбрана следующая схема:
Inner joint — внутренний сустав, качающийся по оси рысканья (yaw)
Mid joint и outer joint — внешние суставы, качающиеся по оси тангажа (pitch). Направление отсчета — от основания ноги к концу ноги.

Угол 0 для всех суставов означает, что нога полностью выпрямлена (прямую ногу будет проще строить в игре).
Задача — при заданной целевой точке найти такие углы поворота сустовов, что-бы конец ноги оказался в заданной точке. Значит время вспоминать тригонометрию.
Угол внутреннего сустава можно найти через арктангенс горизонтальных координат цели.
const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y);С двумя другими суставами посложнее. У нас есть длина всех суставов. Можно найти угол к горизонту и расстояние между средним суставом и землей, а так-же расстояние до целевой точки.
Дальше через теорему косинусов нужно найти углы треугольника по известным сторонам.
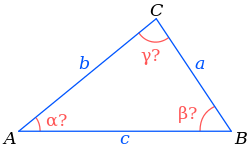

Так это выглядит в коде:
getLegAngles(esimatedLegPosition) { const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y); const dx = Math.hypot(esimatedLegPosition.x, esimatedLegPosition.y) - this.innerJoint.length; const dz = this.step.idlePosition.z + esimatedLegPosition.z; const hyp = Math.hypot(dx, dz); if (hyp > this.midJoint.length + this.outerJoint.length) {//out of reach hyp = this.midJoint.length + this.outerJoint.length; } const innerAngleRad = Math.acos((this.outerJoint.length * this.outerJoint.length - this.midJoint.length * this.midJoint.length - hyp * hyp) / (-2 * this.midJoint.length * hyp)) + Math.atan2(dz, dx); const outerAngleRad = Math.acos((hyp * hyp - this.midJoint.length * this.midJoint.length - this.outerJoint.length * this.outerJoint.length) / (-2 * this.midJoint.length * this.outerJoint.length)) - Math.PI; return { yaw: yawRad, midPitch: innerAngleRad, outerPitch: outerAngleRad }; }Движение
Далее. Робот должен ходить, верно? То-есть мы должны передавать N раз в секунду каждой ноге координаты заданной позиции. С учетом того, что ног 6 и 3 из них двигаются в противофазе получается как-то сложно. Нужно ввести новый уровень абстракции.
А что если мы представим что нога движется по окружности и ей нужно передавать угол обозначающий позицию на этой окружности? Удаление в сторону становится постоянным и нужно передавать только один параметр, меняющийся циклично. Тогда целевые координыты находятся через синус и косинус.
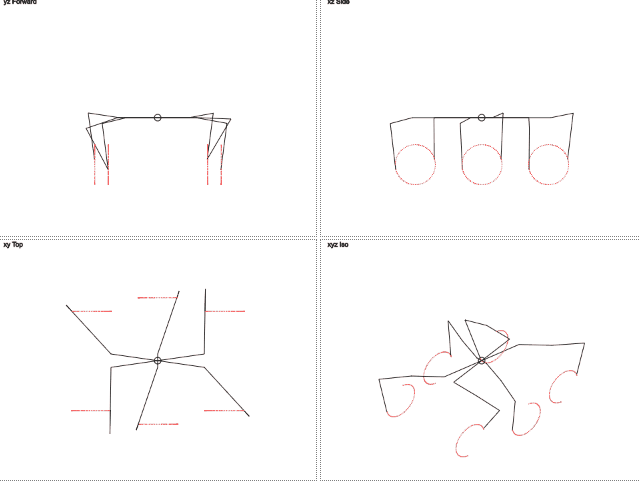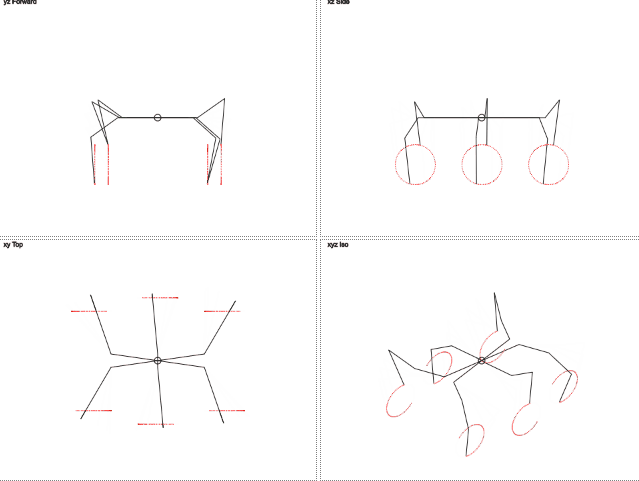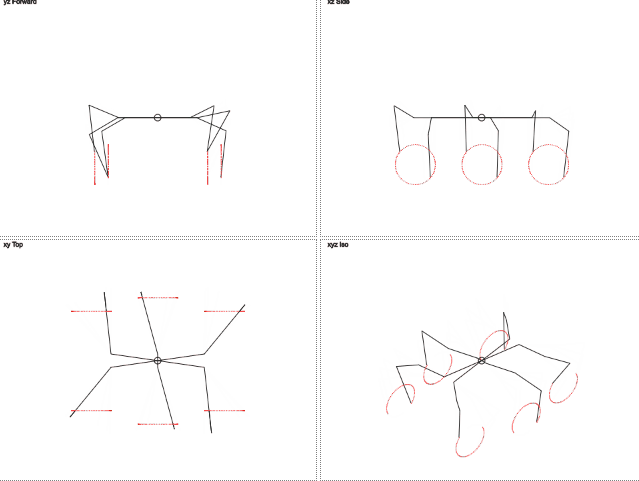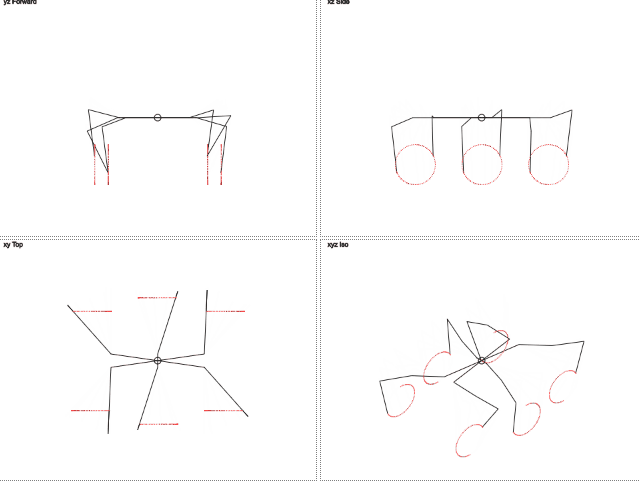
Пока достаточно
Обдумывая как всё будет работать я понял, что задача слишком сложная для того, что-бы всё заработало с первого раза (с дебагом в Space Engineers всё плохо, но об этом в следующей части).
Поэтому я решил написать визуализатор. Мне хотелось его сделать без дополнительных библиотек и иметь возможность запускать его в один клик и без привязки к окружению.
Поэтому был выбран JS + HTML Canvas.
А сейчас нарисуем сову.
Код:
class Vector { constructor(x, y, z) { this.x = x; this.y = y; this.z = z; }; distanceTo(vector) { return Math.sqrt(Math.pow(this.x - vector.x, 2) + Math.pow(this.y - vector.y, 2) + Math.pow(this.z - vector.z, 2)); } diff(vector) { return new Vector( this.x - vector.x, this.y - vector.y, this.z - vector.z ); } add(vector) { return new Vector( this.x + vector.x, this.y + vector.y, this.z + vector.z ); } } Сустав:
class Joint { constructor(angle, position, length) { this.angle = angle; this.position = position; this.length = length; this.targetAngle = angle; this.previousAngle = angle; this.velocity = 0; }; setTargetAngle(targetAngle) { this.targetAngle = targetAngle; this.velocity = this.targetAngle - this.normalizeAngle(this.angle); } normalizeAngle(angle) { while (angle <= -Math.PI) angle += Math.PI * 2; while (angle > Math.PI) angle -= Math.PI * 2; return angle; } getCurrentVelocity() {//per tick return this.normalizeAngle(this.angle - this.previousAngle); } tick() { this.previousAngle = this.angle; this.angle = this.angle + this.velocity; } } Шаг — структура данных для управления ногой:
class Step { constructor( idlePosition,//vector relative to inner joint angle,//step direction length,//step length height,//step height phaseShift// ) { this.idlePosition = idlePosition; this.angle = angle;//radians this.length = length; this.height = height; this.phaseShift = phaseShift; } } Нога:
class Leg { constructor( vehicleCenter, innerJoint, midJoint, outerJoint, step, phaseStep ) { this.vehicleCenter = vehicleCenter; this.innerJoint = innerJoint; this.midJoint = midJoint; this.outerJoint = outerJoint; this.step = step; this.phaseStep = phaseStep; this.innerJoint.length = innerJoint.position.distanceTo(midJoint.position);//calculate this.midJoint.length = midJoint.position.distanceTo(outerJoint.position);//calculate //this.outerJoint.length = 100; this.joints = [innerJoint, midJoint, outerJoint]; this.preCalculateAngles(); } preCalculateAngles() { this.angles = {}; for (let phase = 0; phase < 360; phase += this.phaseStep) { this.angles[phase] = this.getLegAngles(this.getEsimatedLegPosition(phase, this.step.phaseShift)) } } applyStepHeight(z) { const idleYawRad = Math.atan2(this.step.idlePosition.x, this.step.idlePosition.y); const diffHypot = Math.hypot(this.step.idlePosition.x, this.step.idlePosition.y); const minZ = Math.abs(this.midJoint.length - this.outerJoint.length); const maxZ = (this.midJoint.length + this.outerJoint.length) * 0.6; if (Math.hypot(z, 0) > maxZ) { z = z > 0 ? maxZ : -maxZ; } const safeY = (this.innerJoint.length + this.midJoint.length * 0.5 + this.outerJoint.length * 0.5) * Math.cos(idleYawRad); const vAngle = Math.asin(z / safeY); const y = safeY * Math.cos(vAngle) * Math.cos(idleYawRad); this.step.idlePosition.z = z; this.step.idlePosition.y = this.step.idlePosition.y > 0 ? y : -y; this.preCalculateAngles(); } applyStepAngle(angle) { this.step.angle = angle; this.preCalculateAngles(); } applyPhase(phase/*0-360*/) { const legAngles = this.angles[phase]; this.innerJoint.setTargetAngle(legAngles.yaw); this.midJoint.setTargetAngle(legAngles.midPitch); this.outerJoint.setTargetAngle(legAngles.outerPitch); } getEsimatedLegPosition(phase, phaseShift) { phase = (phase + phaseShift) % 360; const stepX = ((phase < 180 ? phase : 180 - phase % 180) / 180 - 0.5) * this.step.length;//linear movement along step direction const stepZ = Math.max(Math.sin(phase * Math.PI / 180), -0.2) * this.step.height / 1.2; //const stepZ = Math.max((phase > 180 ? Math.cos(phase * Math.PI / 360) + 0.9 : Math.cos((phase - 120) * Math.PI / 360)) * .9 - .1, 0) * this.step.height; const x = this.step.idlePosition.x + stepX * Math.cos(this.step.angle); const y = this.step.idlePosition.y + stepX * Math.sin(this.step.angle); return new Vector(x, y, stepZ); } getLegAngles(esimatedLegPosition) { const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y); const dx = Math.hypot(esimatedLegPosition.x, esimatedLegPosition.y) - this.innerJoint.length; const dz = this.step.idlePosition.z + esimatedLegPosition.z; const hyp = Math.hypot(dx, dz); if (hyp > this.midJoint.length + this.outerJoint.length) {//out of reach hyp = this.midJoint.length + this.outerJoint.length; } const innerAngleRad = Math.acos((this.outerJoint.length * this.outerJoint.length - this.midJoint.length * this.midJoint.length - hyp * hyp) / (-2 * this.midJoint.length * hyp)) + Math.atan2(dz, dx); const outerAngleRad = Math.acos((hyp * hyp - this.midJoint.length * this.midJoint.length - this.outerJoint.length * this.outerJoint.length) / (-2 * this.midJoint.length * this.outerJoint.length)) - Math.PI; if (isNaN(yawRad) || isNaN(innerAngleRad) || isNaN(outerAngleRad)) { console.log(yawRad, innerAngleRad, outerAngleRad); console.log(dx, dz); return; } return { yaw: yawRad, midPitch: innerAngleRad, outerPitch: outerAngleRad }; } getMaxMinAngles() { const angles = [0, 90, 180, 270].map((phase) => { return this.getLegAngles(getEsimatedLegPosition(phase, 0)); }); return { yawMin: Math.min(angles.map((x) => { return x.yaw })), yawMax: Math.max(angles.map((x) => { return x.yaw })), midPitchMin: Math.min(angles.map((x) => { return x.midPitch })), midPitchMax: Math.max(angles.map((x) => { return x.midPitch })), outerPitchMin: Math.min(angles.map((x) => { return x.outerPitch })), outerPitchMax: Math.max(angles.map((x) => { return x.outerPitch })), } } tick() { this.joints.forEach(function (joint) { joint.tick(); }); } getVectors() { const res = []; const sinYaw = Math.sin(this.innerJoint.angle); const cosYaw = Math.cos(this.innerJoint.angle); let currentVector = this.vehicleCenter; res.push(currentVector); currentVector = currentVector.add(this.innerJoint.position); res.push(currentVector); currentVector = currentVector.add(new Vector( this.innerJoint.length * sinYaw, this.innerJoint.length * cosYaw, 0 )); res.push(currentVector); const dxMid = Math.cos(this.midJoint.angle) * this.midJoint.length; const dzMid = Math.sin(this.midJoint.angle) * this.midJoint.length; currentVector = currentVector.add(new Vector( dxMid * sinYaw, dxMid * cosYaw, dzMid )); res.push(currentVector); const c = this.midJoint.angle + this.outerJoint.angle; const dxOuter = Math.cos(c) * this.outerJoint.length; const dzOuter = Math.sin(c) * this.outerJoint.length; currentVector = currentVector.add(new Vector( dxOuter * sinYaw, dxOuter * cosYaw, dzOuter )); res.push(currentVector); return res; } } Робот:
class Hexapod { constructor(phaseStep) { this.idleHeight = -70; this.stepAngle = 0; this.turnAngle = 0; this.stepLength = 70; this.stepHeight = 30; this.debugPoints = []; const vehicleCenter = new Vector(0, 0, 0); this.legs = [ new Leg( vehicleCenter, new Joint(0, new Vector(-70, 10, 0), 50), new Joint(0, new Vector(-70, 60, 0), 50), new Joint(0, new Vector(-70, 110, 0), 70), new Step(new Vector(-30, 90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(-70, -10, 0), 50), new Joint(0, new Vector(-70, -60, 0), 50), new Joint(0, new Vector(-70, -110, 0), 70), new Step(new Vector(-30, -90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(0, 10, 0), 50), new Joint(0, new Vector(0, 60, 0), 50), new Joint(0, new Vector(0, 110, 0), 70), new Step(new Vector(0, 100, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(0, -10, 0), 50), new Joint(0, new Vector(0, -60, 0), 50), new Joint(0, new Vector(0, -110, 0), 70), new Step(new Vector(0, -100, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(70, 10, 0), 50), new Joint(0, new Vector(70, 60, 0), 50), new Joint(0, new Vector(70, 110, 0), 70), new Step(new Vector(30, 90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(70, -10, 0), 50), new Joint(0, new Vector(70, -60, 0), 50), new Joint(0, new Vector(70, -110, 0), 70), new Step(new Vector(30, -90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180), phaseStep ), ]; } applyPhase(phase/*0-360*/) { this.legs.forEach(function (leg) { leg.applyPhase(phase); }); } changeHeight(value) { this.legs.forEach(function (leg) { leg.applyStepHeight(this.idleHeight + value); }, this); } changeStepLength(value) { this.stepLength += value; this.legs.forEach(function (leg) { leg.step.length = this.stepLength; leg.preCalculateAngles(); }, this); } applyTurn1(centerX, centerY) { const angleToAxis = Math.atan2(centerX, centerY); const distanceToAxis = Math.hypot(centerX, centerY); distanceToAxis = 1000/distanceToAxis; this.legs.forEach(leg => { const dx = leg.step.idlePosition.x + leg.innerJoint.position.x + Math.sin(angleToAxis)*distanceToAxis || 0; const dy = leg.step.idlePosition.y + leg.innerJoint.position.y + Math.cos(angleToAxis)*distanceToAxis || 0; const angle = Math.atan2(dy,dx); const hypIdle = Math.hypot(dx, dy); leg.applyStepAngle(angle+Math.PI/2); leg.step.length = this.stepLength *hypIdle/ ((distanceToAxis || 0) + 1000); }); } applyTurn(centerX, centerY) { this.stepAngle = Math.atan2(centerX, centerY); if (this.stepAngle > Math.PI / 2) this.stepAngle -= Math.PI; if (this.stepAngle < -Math.PI / 2) this.stepAngle += Math.PI; const mults = this.legs.map(leg => Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x) / Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y + centerY*.3, leg.step.idlePosition.x + leg.innerJoint.position.x + centerX*.3)); const minMult = Math.min(...mults); const maxMult = Math.max(...mults); const mult = minMult / maxMult; const d = Math.pow(Math.max(...this.legs.map(leg =>Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x))),2)/Math.hypot(centerX,centerY); const a = Math.atan2(centerX,centerY); this.legs.forEach(leg => { const dx = leg.step.idlePosition.x + leg.innerJoint.position.x; const dy = leg.step.idlePosition.y + leg.innerJoint.position.y; const idleAngle = Math.atan2(dx, dy) + this.stepAngle; const turnAngle = Math.atan2(dx + centerX, dy + centerY); const hypIdle = Math.hypot(dx, dy); const hyp = Math.hypot(dx + centerX, dy + centerY); leg.applyStepAngle(turnAngle - idleAngle); leg.step.length = this.stepLength * hyp / hypIdle * mult; }); this.debugPoints = [new Vector(Math.sin(a)*-d,Math.cos(a)*-d,0)]; } tick() { this.legs.forEach(function (leg) { leg.tick(); }); } getVectors() { return this.legs.map(function (leg) { return leg.getVectors() }); } } Но для отрисовки понадобятся еще несколько классов:
Обертка над Canvas:
class Canvas { constructor(id, label, axisSelectorX, axisSelectorY) { const self = this; this.id = id; this.label = label; this.canvas = document.getElementById(id); this.ctx = this.canvas.getContext('2d'); this.axisSelectorX = axisSelectorX; this.axisSelectorY = axisSelectorY; this.canvasHeight = this.canvas.offsetHeight; this.canvasWidth = this.canvas.offsetWidth; this.initialY = this.canvasHeight / 2; this.initialX = this.canvasWidth / 2; this.traceCounter = 0; this.maxTraces = 50; this.traces = {}; const axisSize = 150; this.axisVectors = [ [ new Vector(-axisSize, -axisSize, -axisSize), new Vector(-axisSize, -axisSize, axisSize) ], [ new Vector(-axisSize, -axisSize, -axisSize), new Vector(-axisSize, axisSize, -axisSize) ], [ new Vector(-axisSize, -axisSize, -axisSize), new Vector(axisSize, -axisSize, -axisSize) ], ] this.mouseOver = false; this.mousePos = { x: 0, y: 0 };//relative to center this.clickPos = { x: 0, y: 0 };//relative to center this.canvas.addEventListener("mouseenter", function (event) { self.mouseOver = true; }, false); this.canvas.addEventListener("mouseleave", function (event) { self.mouseOver = false; }, false); this.canvas.addEventListener("mousemove", function (event) { if (self.mouseOver) { self.mousePos = { x: event.offsetX - self.initialX, y: event.offsetY - self.initialY }; } }, false); this.canvas.addEventListener("mouseup", function (event) { if (self.mouseOver) { self.clickPos = { x: event.offsetX - self.initialX, y: event.offsetY - self.initialY }; } }, false); }; clear(drawAxis) { this.ctx.clearRect(0, 0, this.canvasWidth, this.canvasHeight); this.ctx.strokeStyle = "#000000"; this.ctx.strokeText(this.label, 10, 10); if (drawAxis) { this.axisVectors.forEach(function (vectors, i) { this.ctx.moveTo(this.initialX, this.initialY); this.ctx.beginPath(); vectors.forEach(function (vector) { this.ctx.lineTo(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector)); }, this); this.ctx.stroke(); const lastVector = vectors[vectors.length - 1]; this.traces[[this.traceCounter, i]] = lastVector }, this); } } drawVectors(vectors) {/*2d array*/ vectors.forEach(function (vectors, i) { this.ctx.moveTo(this.initialX, this.initialY); this.ctx.beginPath(); vectors.forEach(function (vector) { this.ctx.lineTo(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector)); }, this); this.ctx.stroke(); const lastVector = vectors[vectors.length - 1]; this.traces[[this.traceCounter, i]] = lastVector }, this); for (const key in this.traces) { const vector = this.traces[key]; this.ctx.fillStyle = "#FF0000";//red this.ctx.fillRect(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector), 1, 1); } this.ctx.strokeStyle = "#000000"; this.ctx.beginPath(); this.ctx.arc(this.clickPos.x + this.initialX, this.clickPos.y + this.initialY, 5, 0, 2 * Math.PI); this.ctx.stroke(); if (this.mouseOver) { this.ctx.strokeStyle = "#00FF00"; this.ctx.beginPath(); this.ctx.arc(this.mousePos.x + this.initialX, this.mousePos.y + this.initialY, 10, 0, 2 * Math.PI); this.ctx.stroke(); } this.traceCounter = (this.traceCounter + 1) % this.maxTraces; } drawPoints(points) { this.ctx.fillStyle = "#00ff00";//green points.forEach(function (point) { this.ctx.fillRect(this.initialX + this.axisSelectorX(point), this.initialY - this.axisSelectorY(point), 3, 3); }, this); } } В классе Leg есть метод для получения текущих координат суставов. Вот эти координаты мы и будем отрисовывать.
Так-же я добавил отрисовку точек, в которых находилась нога в N последних тиков.
И наконец Worker, который будет запускать симуляцию:
class Worker { constructor(tickTime) { const self = this; this.phaseStep = 5; this.tickTime = tickTime; const tan30 = Math.tan(Math.PI / 6); const scale = 0.7; this.canvases = [ new Canvas('canvasForward', 'yz Forward', function (v) { return v.y }, function (v) { return v.z }), new Canvas('canvasSide', 'xz Side', function (v) { return v.x }, function (v) { return v.z }), new Canvas('canvasTop', 'xy Top', function (v) { return v.x }, function (v) { return -v.y }), new Canvas('canvasIso', 'xyz Iso', function (v) { return v.x * scale + v.y * scale }, function (v) { return v.z * scale + v.x * tan30 * scale - v.y * tan30 * scale }), ]; this.bot = new Hexapod(this.phaseStep); this.phase = 0; this.focus = true; window.addEventListener('focus', function () { console.log('focus'); self.focus = true; }); window.addEventListener('blur', function () { console.log('blur'); self.focus = false; }); this.start(); } tick(argument) { const canvasForward = this.canvases[0]; const bot = this.bot; if (canvasForward.mouseOver) { bot.changeHeight(-canvasForward.mousePos.y); } else { bot.changeHeight(0); } const canvasTop = this.canvases[2]; if (canvasTop.mouseOver) { bot.applyTurn(-canvasTop.mousePos.x, -canvasTop.mousePos.y); } else { bot.applyTurn(0, 0); } this.phase = (this.phase + this.phaseStep) % 360; bot.applyPhase(this.phase); bot.tick(); const vectors = bot.getVectors(); this.canvases.forEach(function (c) { c.clear(false); c.drawVectors(vectors); c.drawPoints(bot.debugPoints); }); } start() { this.stop(); this.interval = setInterval((function (self) { return function () { if (self.focus) { self.tick(); } } })(this), this.tickTime); } stop() { clearInterval(this.interval); } }
Результат:
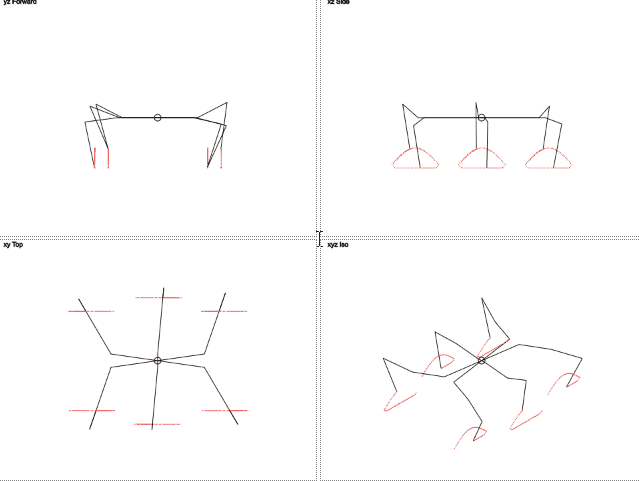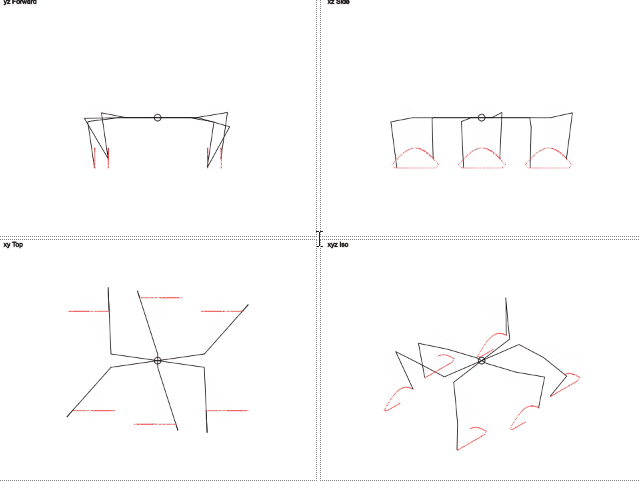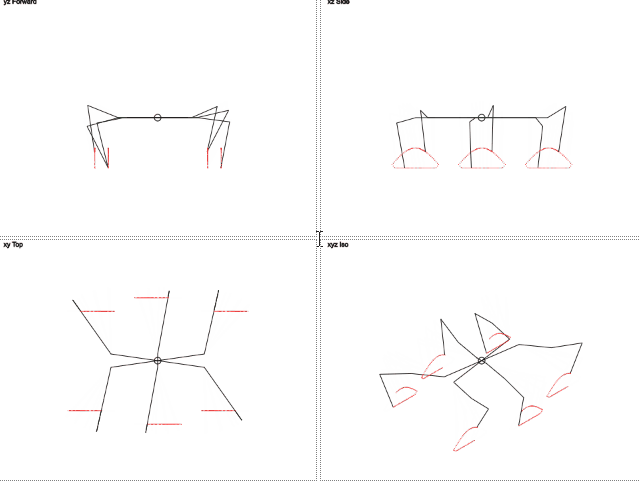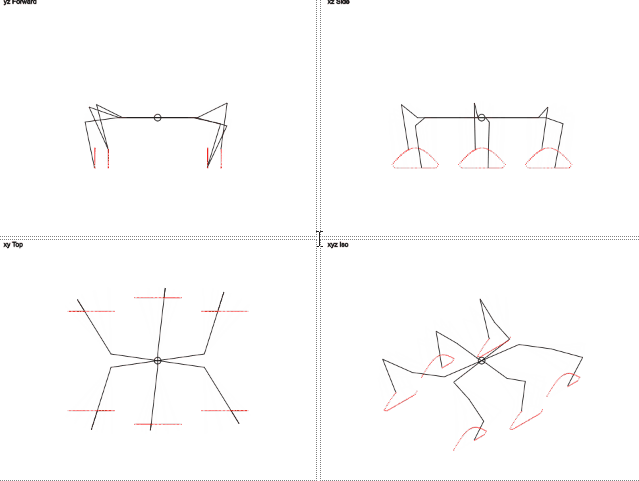
Правда миленько?
Здесь видно, что траектория движения ног отличается от окружности. Движение по вертикали напоминает урезанную синусоиду, а движение по горизонтали линейно. Это должно уменьшить нагрузку на ноги.
Теперь несколько пояснений, что происходит в коде.
Как научить робота поворачивать?
Для поворота я рассмотрел 2 ситуации:
Если робот стоит — ноги двигаются по окружности.
Единственное но — движение именно по окружности сильно усложнило-бы код с текущей реализацией. Поэтому ноги двигаются по касательной к окружности.
Когда робот двигается нужно реализовать что-то вроде Ackermann steering geometry с дифференциалом.
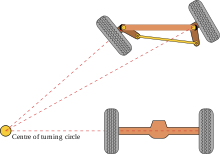
То-есть длина шага ног, двигающихся по меньшему радиусу, — меньше. А угол поворота — больше.
Что-бы реализовать изменение угла поворота для каждой ноги я придумал следующий алгоритм:
1. Считаем угол от изначального положения ноги к центру робота:
const idleAngle = Math.atan2(dx, dy) + this.stepAngle;2. Считаем угол от изначального положения ноги к (центру робота + смещение, которое отвечает за поворот — это изменяемый параметр):
const turnAngle = Math.atan2(dx + centerX, dy + centerY);3. Поворачиваем шаг на разницу этих углов:
leg.applyStepAngle(turnAngle - idleAngle);Но это не всё. Еще нужно измнять длину шага. Реализация в лоб — домножать длину шага на изменение расстояния до центра — имело фатальный недостаток — внешние ноги слишком широко шагали и начинали задевать друг друга.
Поэтому пришлось усложнить реализацию:
1. Считаем изменение расстояния до центра для каждой ноги:
const mults = this.legs.map(leg => Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x) / Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y + centerY*.3, leg.step.idlePosition.x + leg.innerJoint.position.x + centerX*.3));0.3 — магическое число
2. Находим отношение между минимальным и максимальным изменением
const minMult = Math.min(...mults); const maxMult = Math.max(...mults); const mult = minMult / maxMult;Этот множитель отражает разницу между минимальным и максимальным изменением расстояния до центра. Он всегда меньше 1 и если на него домножать длину шага — она при повороте не будет увеличиваться даже для внешних по отношению к направлению поворота ног.
const hypIdle = Math.hypot(dx, dy); const hyp = Math.hypot(dx + centerX, dy + centerY); leg.step.length = this.stepLength * hyp / hypIdle * mult; Вот как это работает (gif 2 мегабайта):
→ Поиграться с результатом можно тут
Для более пристального изучения рекомендую сохранить содержимое в html файл и продолжить в любимом текстовом редакторе.
В следующей публикации я расскажу как заставил всё это работать в Space Engineers.
Спойлер: в Programmable Block можно писать на C# почти последней версии.
Источник


