Как возникают электромагнитные волны

Bremsstrahlung («тормозное излучение») — ударная волна света, которая генерируется, когда заряженные частицы «застревают» в твердом теле (классический процесс генерации излучения в рентгеновских вакуумных трубках).

Для многих вполне естественно ассоциировать электрическое и магнитное поля с векторами и силовыми линиями. Но как этими математическими объектами описать волны? Когда они возникают? Ответы на этот вопрос можно получить с помощью школьных формул с щепоткой специальной теории относительности.

По старой традиции, начинаем плясать от печки. Пусть имеются две заряженные параллельные пластины. Электрическое поле между ними равномерно, и равно нулю снаружи (пренебрегаем краевыми эффектами). Также мы сажаем на систему неподвижную гауссову поверхность — это абстрактная рамка, через которую вычисляется поток векторного поля. Каково электрическое поле нашего конденсатора в системе отсчета, где он находится в движении?

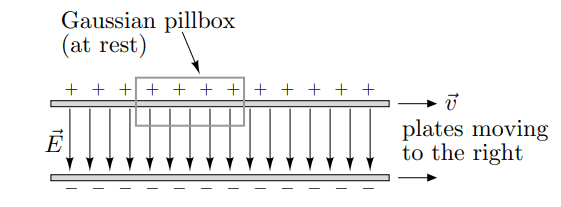
Начнем со случая, где движение происходит в направлении, параллельном пластинам. Они начинают претерпевать лоренцево сокращение, при этом расстояние между ними не меняется, и общий заряд на каждой пластине сохраняется. Далее предполагаем, что читатель провел достаточное количество бессонных ночей разбираясь с парадоксами специальной теории относительности (Чтобы освежевать память, предлагаю просмотреть ламповый советский видеоролик). Таким образом, рамка фиксирует что заряд на единицу площади увеличивается в $$, а поле также возрастает на этот Лоренц-фактор.

Разберем детальней. Гауссова рамка оседлала положительно-заряженную пластину, причем одна грань снаружи, а другая — внутри области ненулевого электрического поля. Применяя закон Гаусса можно показать, что величина электрического поля между пластинами равна

$$

где штрих обозначает величину, измеренную в рамке в которой пластины движутся, а сигма — поверхностная плотность заряда пластины. Поскольку пластины сокращаются по длине, поверхностная плотность заряда отличается от оной для неподвижных пластин вот так

$$

Поглядывая на первую формулу заключаем, что величина поля тоже претерпевает действие лоренцева множителя. То есть, электрическое поле в загрунтованной рамке сильнее, чем в той, что будет двигаться вместе с пластинами.

А как будет выглядеть ситуация, если движение происходит в направлении, перпендикулярном пластинам, то есть параллельно полю Е? В этом случае сокращение длины не влияет на размер пластин, хотя и уменьшает расстояние между ними. Но расстояние между парой близко расположенных, равномерно заряженных пластин не влияет на напряженность поля между ними.

Тогда рассмотрим самый общий случай, когда движение происходит в некотором диагональном направлении относительно поля. В этом случае мы можем рассматривать поле как суперпозицию поля параллельного и поля перпендикулярного движению. Каждое из них как бы порождается своим набором соответствующим образом ориентированных пластин. Затем одна пара пластин сжимается по длине, как описано выше, и вносит вклад в общее поле:

Важно помнить, что такого рода телодвижения применимы только в том случае, если источник поля с точки зрения незакрепленной рамки будет находиться в состоянии покоя. Поскольку всегда существует некоторая система отсчета, в которой любой конкретный источник находится в состоянии покоя, этих уравнений достаточно для решения широкого круга задач. Заметим, что закон преобразования для вектора электрического поля сильно отличается от закона преобразования для обычных векторов перемещения (которые сжимаются в направлении вдоль движения и неизменны в перпендикулярных направлениях).

Равномерное движение точечного заряда

Следующим шагом будет рассмотрение поля единичного точечного заряда, движущегося с постоянной скоростью. В своей системе покоя электрическое поле положительного точечного заряда имеет одинаковую силу во всех направлениях. Как выглядит это поле в какой-то другой системе отсчета? Применяя наш подход к неоднородному электрическому полю, мы должны быть очень осторожны, так как придется следить не только за величиной поля, но и за тем, где оно имеет эту величину. Поэтому представим себе, что наш точечный заряд окружен сферической оболочкой. В нашей системе отсчета и частица, и ее сфера движутся.

Таким образом, сокращение длины говорит о том, что сфера сплющивается в сфероид, как показано в поперечном сечении на рисунке:

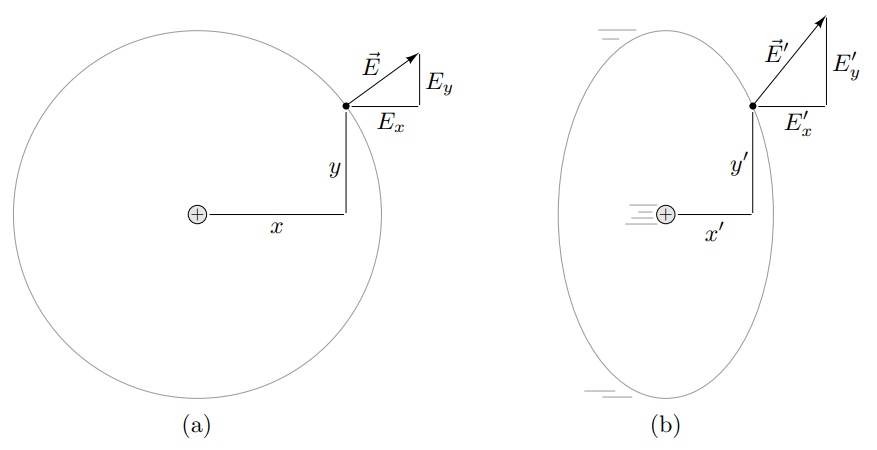
(a) Точечный заряд в состоянии покоя, окруженный воображаемой сферой. Электрическое поле в любой точке сферы направлено прямо в сторону от заряда. (b) В системе отсчета, где заряд и сфера движутся вправо, сфера сжимается по длине, но вертикальная составляющая поля становится сильнее. Эти два эффекта объединяются, чтобы заставить поле снова указывать прямо от текущего местоположения заряда.

Теперь рассмотрим величину электрического поля в некой точке поверхности сферы. Ее координата имеет х и у компоненты. Вектор поля идущий от заряда через эту некую точку также вполне представим как пара компонент, причем справедливо соотношение:

$$

В нашей системе отсчета, где заряд движется, длина x в направлении движения уменьшается:

$$

(в то время как y-составляющая смещения одинакова в обоих случаях). Однако, согласно результатам предыдущего раздела, y-составляющая поля усиливается аналогичным множителем:

$$

(в то время как х-компонента поля одинакова на обеих картинках). Таким образом, соотношение компонентов поля

$$

Другими словами, поле в фиксированной рамке указывает прямо на заряд, как и в движущейся. Накидаем схематически электрическое поле точечного заряда, движущегося с постоянной скоростью:

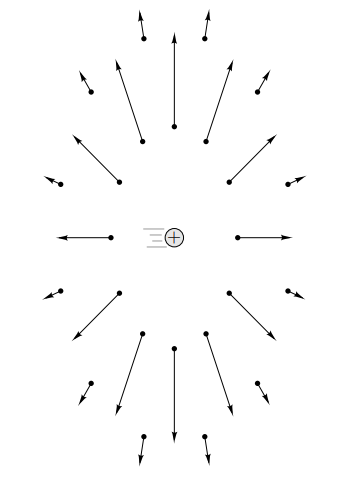
Электрическое поле точечного заряда движущегося вправо с постоянной скоростью, равной 4/5 скорости света.

Чем быстрее движется заряд, тем заметнее становится усиление перпендикулярной составляющей поля. Если скорость заряда намного меньше скорости света, то это усиление часто пренебрежимо мало.

Поле ускоряющегося заряда

Итак, когда точечный заряд движется с постоянной скоростью, его электрическое поле всегда направлено прямо от него, радиально. В свете специальной теории относительности это может показаться странным, поскольку никакая информация не может перемещаться быстрее скорости света. Почему же тогда поле в каком-то отдаленном месте указывает прямо на то место, где заряд находится сейчас, а не на то, где он был некоторое время назад? Означает ли это, что информация о движении заряда мгновенно распространяется по всей Вселенной? Ну, не обязательно.

Видите ли, частица уже некоторое время движется с постоянной скоростью по предсказуемому курсу. Поэтому, если вы находитесь в далеком месте, вы могли бы организоваться так, чтобы частица посылала вам информацию о своем положении и скорости, а вы, получив эту информацию, экстраполировали бы движение чтобы выяснить, где частица должна находиться. Однако ваша схема предсказания положения частицы будет разрушена, если частица претерпит некоторое ускорение между тем моментом, когда она послала вам информацию, и настоящим.

Вы могли бы подумать, что частица продолжает двигаться с постоянной скоростью, и поле в вашем местоположении указывало бы в сторону того места, где частица была бы сейчас, если бы не было факта ускорения. Но на самом деле частицы там нет.

Например, предположим, что частица сначала движется вправо со скоростью 1/4 скорости света, а затем внезапно отскакивает от стены и с той же скоростью летит обратно. Через одну секунду новость об отскоке не могла пройти дальше одной световой секунды (300 000 км). Если вы находитесь ближе, чем на одну световую секунду к месту отскока, то вы уже получили известие, и поле в вашем местоположении указывает туда, где сейчас находится частица. Но если вы находитесь дальше, чем на одну световую секунду от места отскока, то новость еще не дошла до вас, и поле в вашем местоположении указывает туда, где частица была бы сейчас, если бы не было отскока.

Положительно заряженная частица, первоначально движущаяся вправо со скоростью 1/4 скорости света, отскакивает от стены в точке В. Частица сейчас находится в точке А, но если бы не было отскока, она была бы сейчас в точке С. Окружность (фактически поперечное сечение сферы) охватывает область пространства, в которую уже поступила новость об отскоке; внутри этой окружности (как в точке D) электрическое поле указывает прямо на точку A. Вне окружности (как в точке E) новость еще не поступила, поэтому поле указывает прямо на точку C. Со временем круг расширяется наружу со скоростью света, а точки А и С удаляются от точки В со скоростью 1/4 скорости света.

Из специальной теории относительности мы знаем, что никакая информация не может перемещаться быстрее скорости света. Предположим наилучший возможный случай: информация распространяется точно со скоростью света, но не быстрее. Этого предположения вместе с законом Гаусса достаточно, чтобы определить электрическое поле повсюду вокруг ускоренного заряда. Полная карта электрического поля ускоренного заряда оказывается довольно сложной. Вместо того чтобы представлять поле в виде пучка стрелок, гораздо удобнее использовать более абстрактное представление в виде линий поля. Силовые линии — это непрерывные линии в пространстве, идущие параллельно направлению электрического поля. Таким образом, рисунок силовых линий в некой области немедленно сообщает нам направление электрического поля, хоть определить его величину и не так просто.

Так будет выглядеть карта полевых линий для нашей ситуации

Линии поля через серую сферическую оболочку опускаем, так как эта область как раз в разгаре получения новостей об ускорении частицы. Чтобы определять направление поля здесь, представьте, что гауссовская рамка изогнута (на рисунке обозначена пунктирной линией, которая оседлает серую оболочку. Эта поверхность должна быть симметричной относительно линии, по которой движется частица; если смотреть вдоль этой линии, рамка будет круглой).

Гауссова поверхность не содержит электрического заряда, поэтому закон Гаусса говорит нам, что полный поток E через нее должен быть равен нулю. Теперь рассмотрим поток, проходящий через различные части поверхности. На внешней (правой) части есть положительный поток, в то время как на внутренней (левой) части есть отрицательный поток. Но эти два вклада в поток не отменяют друг друга, так как поле значительно сильнее снаружи, чем внутри. Это происходит потому, что поле снаружи — это поле точечного заряда, расположенного в точке С, в то время как поле внутри — это поле точечного заряда, расположенного в точке А, и С значительно ближе, чем А. Таким образом, общий поток через внутреннюю и внешнюю части поверхности является положительным. Чтобы отменить этот положительный поток, остальные края рамки должны пропускать отрицательный поток.

Таким образом, электрическое поле внутри серой оболочки должно иметь ненулевую составляющую вдоль оболочки, по направлению к центру гауссовой поверхности. Будем называть эту составляющую поперечным полем, поскольку она указывает в поперечном (то есть перпендикулярном) чисто радиальном направлении поля с обеих сторон. Чтобы быть более точными относительно направления поля внутри серой оболочки, рассмотрим модифицированную гауссову поверхность

Ужимаем внешнюю поверхность ef до тех пор, пока она не уменьшится до того же угла относительно точки С, что и внутренняя поверхность ab, если смотреть с точки A. Теперь потоки через ab и ef действительно взаимокомпенсируются. Отрезки bc и de выбраны так, чтобы они были точно параллельны линиям поля в их местоположении, поэтому поток через эти участки поверхности отсутствует.

И тогда, для того, чтобы общий поток был равен нулю, он должен быть нулевым и через сегмент cd. Это означает, что электрическое поле внутри серой оболочки должно быть параллельно cd. Если стартануть с точки А и пойти по любой линии поля наружу, то придется навернуть резкий угол на внутреннем краю серой оболочки, а затем пройти вдоль оболочки и медленно выйти наружу, сделав еще один резкий поворот на внешнем краю. (Толщина серой оболочки определяется длительностью ускорения заряда.)

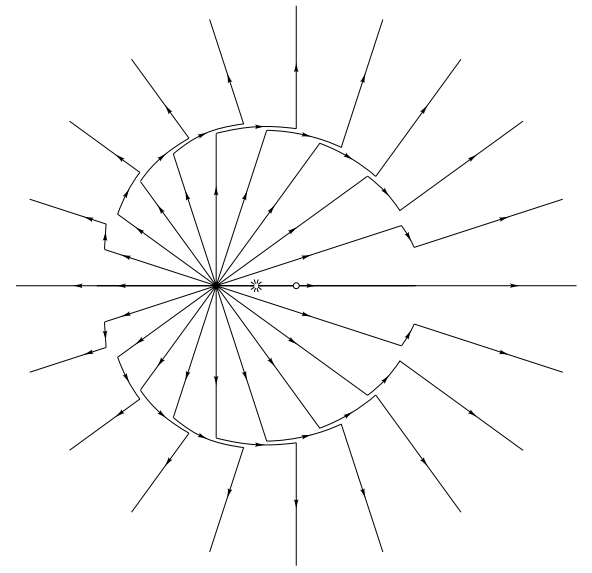
И вот выходит итоговая иллюстрация силовых линий. Поперечная часть электрического поля ускоренного заряда также называется полем излучения, поскольку со временем она «излучается» наружу в сферу, расширяющуюся со скоростью света. Если ускорение заряженной частицы достаточно велико, то поле излучения может быть достаточно сильным, воздействуя на далекие заряды гораздо сильнее, чем обычное радиальное поле заряда, движущегося с постоянной скоростью. Поле излучения может также накапливать относительно большое количество энергии, которая уносится от создавшего ее заряда.

Сила поля излучения

Чтобы превратить качественные идеи предыдущего раздела в количественные формулы,
рассмотрим несколько более простую ситуацию, в которой положительно заряженная частица вначале летит вправо, а потом внезапно останавливается. Пусть v₀ — начальная скорость, и пусть замедление начинается в момент времени t = 0 и заканчивается в момент времени t = t₀. Предположим, что ускорение является постоянным в течение этого временного интервала:

$$

Также положим, что v₀ намного меньше скорости света, так что релятивистское сжатие и растяжение электрического поля, обсуждаемые ранее, пренебрежимо малы. Покажем ситуацию в некоторый момент времени T, значительно более поздний, чем t₀. «Импульс» излучения содержится в сферической оболочке толщиной ct₀ и радиусом cT. Вне этой оболочки электрическое поле указывает в сторону от того места, где была бы частица, если бы она продолжала двигаться; эта точка находится на расстоянии v₀T справа от ее фактического местоположения. (Расстояние, пройденное во время торможения ничтожно мало в этом масштабе.) На рисунке для ясности показана только одна полевая линия, выходящая под углом θ от направления движения частицы. В этой линии есть резкий изгиб, когда она проходит через оболочку, как обсуждалось выше. Мы хотели бы знать, насколько сильно электрическое поле внутри оболочки.

Давайте разберем искривленное поле на две составляющие: радиальную составляющую $$, которая указывает в сторону от местоположения частицы, и поперечную составляющую $$, которая указывает в перпендикулярном направлении

Соотношение этих компонентов определяется направлением излома

$$

Мы можем найти радиальную компоненту, применив закон Гаусса к крошечной рамке, расположенной на внутренней поверхности оболочки (Gaussian pillbox на рисунке). Пусть стороны рамки будут бесконечно короткими, чтобы поток через них был ничтожен. Тогда, поскольку чистый поток через рамку равен нулю, радиальная составляющая вектора E (то есть составляющая, перпендикулярная верхней и нижней частям рамки) должна быть одинаковой с каждой стороны внутренней поверхности оболочки. Но внутри сферы излучения электрическое поле задается законом Кулона. Таким образом, радиальная составляющая искривленного поля равна

$$

где q — заряд частицы. Подставим это уравнение в предыдущее и используем тот факт, что R = cT:

$$

Хотя выражение выводилось для частного случая, когда конечная скорость частицы равна нулю, оно верно и в более общих случаях. (Чтобы убедиться в этом, рассмотрите случай, когда частица сначала находится в состоянии покоя, а затем получает внезапный удар вправо).

Таким образом, у нас есть все, что нужно знать о силе импульса излучения. Во-первых, обратите внимание, что поперечное поле пропорционально 1/R, а не квадрату. Это означает, что с течением времени и увеличением R, поперечное поле становится намного сильнее радиального; на очень больших расстояниях радиальным полем можно полностью пренебречь, и поле будет чисто поперечным. Во-вторых, рассмотрим зависимость $$ от угла θ: она слабее всего вдоль направления движения (θ = 0 или 180°) и сильнее всего под прямым углом к движению (θ = 90°). Оглядываясь на предыдущий рисунок, мы видим, что размер излома в поле является качественным показателем напряженности поля. Наконец, обратите внимание, что сила поперечного поля пропорциональна а, величине ускорения частицы. Чем больше ускорение, тем сильнее импульс излучения.

Этот импульс излучения несет в себе энергию. Вспомним из электростатики, что энергия на единицу объема, запасенная в любом электрическом поле, пропорциональна квадрату напряженности поля. В нашем случае это подразумевает

$$

Поскольку объем сферической оболочки (самой оболочки, а не области, которую она охватывает) пропорционален квадрату радиуса, полная энергия, содержащаяся в ней, не изменяется с течением времени и увеличением R. Таким образом, когда заряженная частица ускоряется, она теряет энергию для своего окружения в количестве, пропорциональном квадрату ее ускорения. Этот процесс является основным механизмом, лежащим в основе всего электромагнитного излучения: видимого света и его невидимых собратьев, от радиоволн до гамма-лучей.

Формула Лармора

Теперь можно перейти к приложениям. Выведем точную формулу для энергии, излучаемой ускоренной заряженной частицей. Энергия на единицу объема, запасенная в любом электрическом поле, равна

$$

Как только импульс становится достаточно большим, мы можем пренебречь радиальной составляющей поля и просто подключить $$ для $$. В результате получается

$$

Если нас не волнует направление, в котором идет энергия, то удобно усреднить уравнение по всем направлениям. Провернем один математический трюк. Введем координатную систему с началом координат в центре сферы и осью вдоль первоначального направления движения частицы. Тогда для любой точки (x, y, z) на сферической оболочке cosθ = x/R. Используя угловые скобки〈 〉для обозначения среднего значения по всем точкам на оболочке, запишем тождество

$$

Теперь, поскольку начало координат находится в центре сферы, придется согласиться, что среднее значение квадрата икс равно среднему значению и для квадратов других компонент:

$$

но тогда выходит, что

$$

Ну, а так как $$ и R — константа по всей оболочке, то:

$$

Таким образом, средняя энергия на единицу объема, запасенная в поперечном электрическом поле, равна

$$

Для получения полной энергии, накопленной в поперечном электрическом поле, необходимо умножить полученное выражение на объем сферической оболочки. Площадь поверхности оболочки равна 4πR², а ее толщина — ct₀, поэтому ее объем является произведением этих множителей. Тогда общая энергия

$$

Заметим, что полная энергия не зависит от R; то есть оболочка несет в себе фиксированное количество энергии, которое не уменьшается по мере ее расширения. До сих пор в обсуждениях фигурировало только электрическое поле ускоренного заряда. Но оказывается, что есть еще и магнитное поле, которое уносит равное количество энергии. В принципе, ошибка в два раза не так существенна для нашей формулы, но все же будем честными. Оставим все интересности связанные с магнитным полем на следующий раз, а пока все же учтем, что суммарная энергия, переносимая импульсом излучения, в два раза больше, чем в последнем уравнении, или

$$

Обычно удобнее разделить обе стороны этого уравнения на длительность ускорения частицы t₀. Левая сторона тогда становится энергией, излучаемой частицей в единицу времени, или мощностью, выделяемой во время ускорения:

$$

Этот результат называется формула Лармора, так как он был впервые получен (с использованием более сложного метода) Джозефом Лармором в 1897 году. Вывод, приведенный здесь, был впервые опубликован Джозефом Томсоном (первооткрывателем электрона) в 1907 году. Хотя наш вывод опиратся на частный случай, когда конечная скорость частицы равна нулю, формула Лармора справедлива для любого вида ускоренного движения при условии, что скорость частицы всегда намного меньше скорости света. В любом случае, можно сделать и обобщение на релятивистский случай.

Электромагнитные Волны

В предыдущем разделе мы пришли к выводу, что когда заряженная частица ускоряется, часть ее электрического поля вырывается на свободу и удаляется со скоростью света, образуя импульс электромагнитного излучения. Часто на практике заряженные частицы непрерывно колеблются взад и вперед, посылая один импульс за другим в периодической последовательности. Вот пример электрического поля вокруг колеблющегося заряда

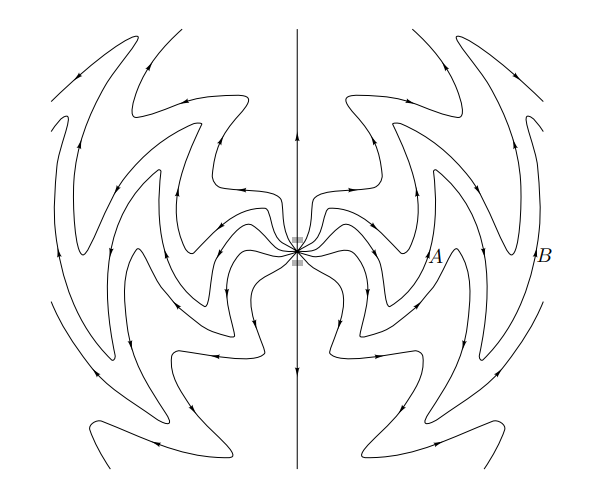
Если проследить прямую линию от заряда в центре рисунка, можно заметить, что поле колеблется взад и вперед. Расстояние, на котором повторяется направление поля, называется длиной волны. Например, точки А и В находятся на расстоянии одной длины волны друг от друга.

Если вы сидите в неподвижной точке и наблюдаете, как электрическое поле проходит мимо, вы обнаружите, что его направление колеблется. Время, за которое паттерн повторяется один раз, называется периодом волны и равно времени, за которое заряд источника повторяет один цикл своего движения. Период также равен времени, за которое волна проходит расстояние в одну длину волны. Поскольку она движется со скоростью света, мы можем заключить, что длина волны и период связаны пропорцией

$$

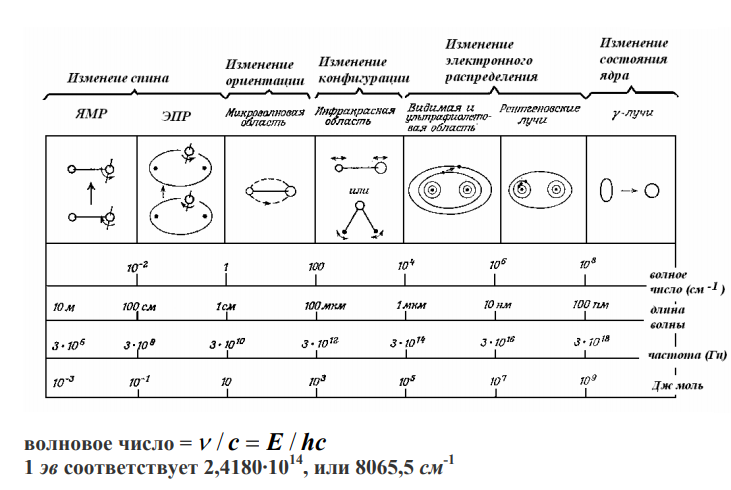
где λ («лямбда») — стандартный символ для длины волны, а Т — это стандартный символ для периода, и с — скорость света. Частота колебания обратнопропорциональна периоду. Из соображений традиции и удобства, электромагнитные волны разной длины называются по-разному. Радиоволны с длиной волны в метр и более генерируются относительно легко, когда заряд проходит вверх и вниз по антенне. Несколько более короткие длины волн используются для телевизионной и микроволновой связи. Инфракрасные волны — длина волны от миллиметра до 700 нанометров; случайные микроскопические движения, присутствующие во всей материи при комнатной температуре, вызывают излучение инфракрасного излучения с длиной волны около сотой доли миллиметра. Более горячие объекты, такие как Солнце, испускают излучение в видимом спектре, который охватывает диапазон 400-700 нанометров, к которому чувствителен человеческий глаз. Длина волны видимого света определяет его цвет, причем красный свет имеет самую длинную длину волны, а фиолетовый — самую короткую. Еще более коротковолновые волны относятся к ультрафиолетовым, рентгеновским и гамма-лучам.

Почему небо голубое?

Солнце испускает видимый свет всех цветов, который бомбардирует атмосферу Земли. Атмосфера относительно прозрачна для большей части этого света. Но если бы атмосфера была полностью прозрачной, небо казалось бы черным. По-видимому, часть света от Солнца рассеивается или отклоняется молекулами воздуха. Когда мы смотрим на небо в направлении от Солнца, мы видим этот рассеянный свет, который в основном синий, и наоборот, красный свет легче проходит толщу атмосферы, что делает его видимым, когда Солнце находится вблизи горизонта. Но почему молекулы воздуха рассеивают синий свет больше, чем красный? Очевидно, короткие волны рассеиваются гораздо сильнее, чем длинные. Мы можем понять это явление, представив простую модель процесса рассеяния и применив результаты вышепроведенных выкладок, согласно которым энергия, излучаемая ускоренным зарядом, пропорциональна квадрату ускорения. Рассмотрим один атом азота или кислорода в атмосфере.

Для наших целей лучше всего представить атом как крошечную точку с положительным зарядом (ядро), окруженную большим облаком размазанного отрицательного заряда (электроны). Заряды компенсируются, и атом электрически нейтрален. Теперь предположим, что мимо проходит электромагнитная волна. Электрическое поле в месте расположения атома сначала указывает вверх, затем вниз, затем снова вверх, снова вниз… (Для видимого света длина волны намного больше, чем размер атома.) Хотя нейтральный атом не чувствует чистой силы от этого электрического поля, его составляющие действительно чувствуют силы, поэтому они слегка отклоняются в противоположных направлениях. Впрочем, далеко они не уходят, так как потенциал дает о себе знать. Это похоже на то, как если бы электроны и ядро были соединены вместе жесткой пружиной. Когда волна проходит мимо, ядро слегка колеблется вверх и вниз на той же частоте, что и волна. Мы можем описать его положение как:

$$

где ω = 2πc/λ и λ-длина волны. Пока «пружина» очень жесткая, амплитуда x₀ будет зависеть только от силы электрического поля, а не от длины волны. Поскольку ядро колеблется вверх и вниз, оно само испускает электромагнитное излучение с одинаковой частотой и длиной волны. Согласно предыдущим пунктам, излучаемая энергия пропорциональна квадрату ускорения. Ускорение ядра определяется как вторая производная его положения:

$$

Теперь мы можем определить, как количество излучаемой энергии зависит от длины волны:

$$

Эта формула гласит, что коротковолновая волна заставляет ядро излучать гораздо больше энергии, чем длинноволновая. То же самое верно и в отношении излучения, испускаемого электронами, которые колеблются в противоположном направлении с той же частотой. Это электромагнитное излучение, испускаемое атомом, несет в себе энергию, и энергия должна откуда-то браться. Должно быть правдоподобным, что энергия исходит от поступающей волны, возбуждающей атомные колебания. Эта волна продолжает свой путь, но часть ее энергии была потеряна. Не будем вдаваться в точный механизм этого процесса на данном этапе — просто уповаем на сохранение энергии.

Таким образом, можно заключить, что когда проходит световая волна, атом забирает из нее некоторую энергию и вновь излучает эту энергию как волну той же длины во все направления. Из последнего уравнения видно, что этот процесс гораздо эффективнее для коротковолнового (то есть фиолетового и синего) света, чем для длинноволнового. Вот почему небо голубое. И наоборот, когда смесь различных цветов света проходит через большое количество воздуха, большая часть синего света удаляется, оставляя в основном красный. Вот почему так прекрасны закаты.

P.S.

Кто-то может возразить, дескать, небо фиолетовое, но на восприятии человека сказывается предрасположенность к синему спектру из-за строения колбочек в глазах, да и вообще, в ваших расчетах слишком много частностей и допущений. Наиболее правильным будет обратить его внимание на неравномерность интенсивности спектра Солнца. А более строгий вывод формулы Лармора осуществляется через уравнения Максвелла, потенциалы Лиенара-Вихерта и функции Грина. Подобные строгие выкладки приводят к тому же результату и описаны во многих книжках по электродинамике (Например Е.Ю.Петров Излучение электромагнитных волн движущимися заряженными частицами). Мы же использовали лекционные наброски Дэниела Шрёдера, который в свою очередь опирался на потрясающий учебник Эдварда Перселла «Электричество и магнетизм», что во многом наглядней и более интуитивно.