Как в Индиане чуть не узаконили π = 3.2

Поздравляю всех с (прошедшим) днем числа Пи! (день числа Пи отмечается 14 марта, поскольку эта дата в американском формате записывается в как 3.14 — прим. перев.) Чтобы отметить его как следует, я хочу ненадолго отвлечься от программного обеспечения и поговорить о чем-то особом. Возможно, вы слышали байку о том, как в штате Индиана пытались законодательно приравнять число Пи к чем-то типа 3, или 4, или 3.15. Обычно ее рассказывают в качестве доказательства того, что жители Индианы — бестолковая деревенщина, но это далеко не вся история. Зачем они пытались поменять значение π и на что они рассчитывали?

_{Предвосхищая комментарии: конечно, я знаю про константу τ и считаю ее более уместной для описания свойств круга. Однако никто не пытался поменять ее значение на законодательном уровне, не так ли?}

Я занялся исследованием, и теперь могу рассказать историю целиком. Чтобы вы поняли контекст, мне придется объяснить кое-какие математические концепции.

Мне придется объяснить немало математических концепций.

Линейка и циркуль

Западная математическая традиция берет свое начало из Греции. Они были не первой цивилизацией, занимавшейся математикой, и многие приписываемые им вещи были открыты еще раньше математиками из Вавилона, Египта и Китая — однако эти исследования дошли до нас через античную Грецию. Также греки того времени имели неоспоримое превосходство в области геометрии, и особенно интересовались классом задач, называемым «Построение с помощью циркуля и линейки».

Если у вас есть бесконечно длинная неградуированная линейка и циркуль, какие формы вы можете построить и что можно получить из существующих форм? Сделать можно гораздо больше, чем вы думаете. Например, можно взять угол и получить его бисекцию, то есть провести линию, разделяющую его ровно пополам. Можно взять линию и построить из нее 32-угольник. Можно взять квадрат и построить другой квадрат, площадь которого будет ровно в 2 раза больше.

Некоторые задачи на построение греки так и не решили, однако это не значило, что задача нерешаема вообще. Некоторые слишком сложные для античности задачи были решены позже, например построение 17-угольника (решена в 1796 году). Одна из самых долго обсуждаемых задач такого рода называлась «квадратура круга»: если у вас есть круг, можно ли построить квадрат точно такой же площади?

Теперь нужно очень точно сформулировать, что это значит. Если вы можете построить квадрат с погрешностью 0.00001% — это не считается. Если вы придумаете способ, решение которого будет стремиться к точному значению за бесконечное количество шагов — это не считается. Также не считается решение, требующее что-либо еще помимо немаркированной линейки и циркуля. Греки уже знали способ найти квадратуру круга с помощью градуированной линейки или архимедовой спирали — вопрос был именно в том, можно ли получить точную площадь с минимумом инструментов.

К эпохе Возрождения математики сходились во мнении, что это скорее всего невозможно, поскольку все мыслимые попытки провалились. В 1837 году ученый Пьер Ванцель подвел под это утверждение твердый фундамент. Площадь круга с радиусом 1 будет равна π, следовательно стороны квадрата должны иметь длину, равную √π. Ванцель доказал, что это значение можно получить только в том случае, если бы π было алгебраическим числом, а математики подозревали, что оно на самом деле трансцендентное.

Алгебраическое? Трансцендентное? Я позаимствую объяснение, написанное Марком Доминусом:

Сыграем в игру. Возьмите произвольное число X. Дальше вы можете использовать сложение, вычитание, деление и умножение на любое целое число. Вы также можете умножать результат на X. Операции можно производить сколько угодно раз. Если в результате вы получите 0 — вы победили.

Например, X = 2/3. Умножаем на 3, вычитаем 2, получаем 0 — вы победили!

Допустим, X равен ∛7. Умножаем на X, потом еще раз, потом вычитаем 7. Вы снова победили!

Теперь допустим, что X = √2 + √3. Тут увидеть решение уже не так просто. Но оказывается, что если умножить на X, вычесть 10, дважды умножить на X, а потом добавить 1, то вы тоже победите. Это абсолютно неочевидно, но вы можете попробовать выполнить это на калькуляторе.

А вот если X = π — вы не можете выиграть. Нет такого способа, позволившего бы получить 0 с помощью разрешенных действий, сколько бы раз вы их не повторяли. Это также очень хитрая, неочевидная штука.

Числа, с которыми вы можете победить, называются алгебраическими. Числа вроде π, с которыми вы не можете, называются трансцендентными.

Хотя «почти все» числа являются трансцендентными, доказать что конкретное число является таковым очень сложно. Мы даже не знаем, является ли таковым значение π + e. Тем не менее, в 1882 году Фердинанд фон Линдеманн доказал трансцендентность числа π — это значит, что построить сторону квадрата длиной √π невозможно, а следовательно и построить квадратуру круга тоже нельзя.

_{Быстрый набросок доказательства: действительные числа являются неисчислимыми. Каждое алгебраическое число является корнем некого полинома. Полиномы могут быть представлены в виде кортежа коэффициентов, например: x^2 — 3 → (1, 0, -3). Множество всех конечных списков является счетным, следовательно алгебраические числа также счетны. Если вычесть из несчетного множества действительных чисел счетное множество алгебраических, останутся трансцендентные.}

Хочу еще раз подчеркнуть, что это практически не влияет на настоящие прикладные задачи. Получить приближенное решение легко, а если вам позарез необходимо получить точное значение — можно взять линейку с делениями.

Мракобесы

Даже после того, как математики доказали невозможность построения квадратуры круга, существует группа людей, продолжающих с энтузиазмом искать решения: мракобесы.

Мракобесы — это люди, глубоко и непоколебимо убежденные в чем-то внешне похожем на научные исследования, но на самом деле являющемся бредом сивой кобылы. Для завсегдатаев интернета самым известным примером наверняка является куб времени. Большинство мракобесов говорят более осмысленно, но руководствуются такой же инопланетной логикой. В любой области такие ребята есть: например, мракобесы от информатики опровергают проблему останова, доказывают равенство P и NP, и выдают вот такие охренительные шедевры _{(нет, серьезно, посмотрите — это божественно!)}.

Мракобесов в области математики также немало, и порядочное их число озабочены квадратурой круга и трисекцией угла. Я думаю, что причины следующие:

1. Задачу легко понять обывателю.

2. Задача известна за пределами математического сообщества. Мракобесов, решающих проблему Гольдбаха, гораздо меньше (но они тоже есть).

3. Задача выглядит так, будто ее можно «попытаться решить» без каких-либо познаний в математике: просто делай построения до тех пор, пока что-нибудь не получится.

4. Легко посчитать задачу решенной, если вы не понимаете нюансов насчет точного решения и использования только линейки и циркуля.

В книге «A Budget of Paradoxes» Огастес Де Морган упоминает более тридцати «квадратурщиков», с которыми он вел переписку. Читая его заметки из 1872 года, не перестаешь удивляться тому, как похожи тогдашние мракобесы на нынешних. Именно поэтому мракобесие настолько меня завораживает — в нем безумие противоречит конформизму. Какими бы ни были предметная область и эра, какие бы слова ни произносил мракобес — они всегда идут по тому же сценарию и говорят одно и то же. Именно поэтому мракобесие можно распознать, даже не вчитываясь — по соответствию форме все становится понятно. Это научная версия того, что в искусстве называют «ар-брют«.

Эдвард Дж. Гудвин

Мракобесие возникает по-разному. В случае с Эдвардом Дж. Гудманом, к несчастью, причиной было психическое заболевание. Он считал, что доказательства ниспосланы ему свыше — в прямом смысле слова Бога. В 1888 году Бог рассказал ему, как построить квадратуру круга. Полное описание метода можно прочитать здесь, но вот его краткое содержание: сначала берем 90-градусную дугу и проводим хорду между ее концами. Отношение длины дуги к хорде будет равно 8:7, а длины хорды к основанию треугольника — 10:7. Из произведения этих величин следует, что длина основания равна 4/5 длины дуги, а поскольку мы рассматривали только четверть круга, то умножение на 4 даст нам искомое значение: 16/5. Далее построение является тривиальным.

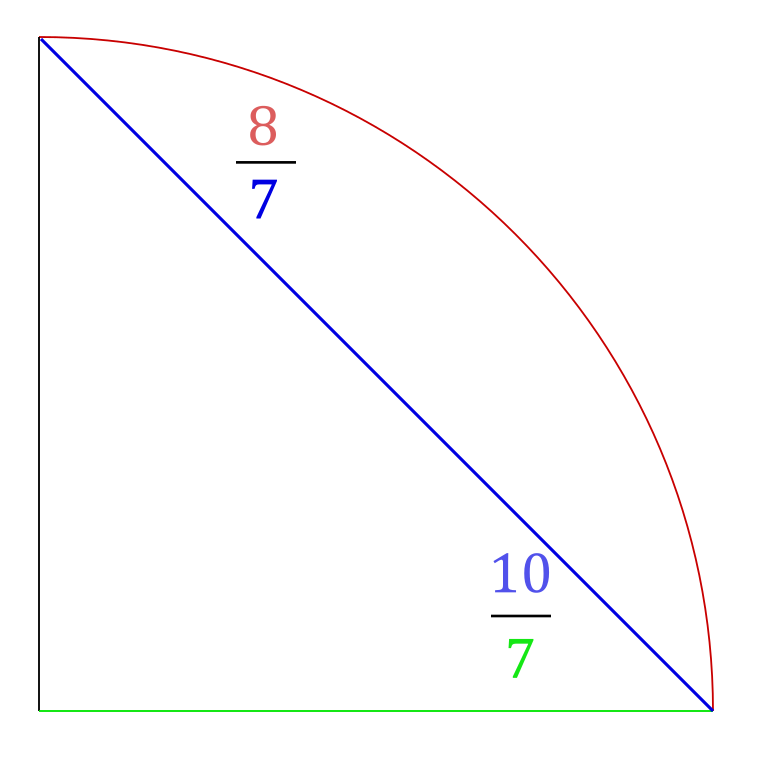
Уследили за ходом мысли? Надеюсь, что нет! Я потратил три часа, разглядывая это доказательство и пытаясь понять, что, черт возьми, творилось у него в голове. Должен сказать, что заставить себя думать как мракобес отнюдь не просто. Теперь эта инопланетная логика отпечаталась у меня в голове. Я на один шаг приблизился к тому, чтобы самому стать мракобесом. Чего я только не делаю ради вас!

Самое важное для нашей истории — это соотношения, которые он использовал: 8:7 и 10:7. Они примерно на 2% и 1% отличаются от настоящих значений π/2 и √2 соответственно, и из них мы можем получить значение π c погрешностью примерно 4% (160/49). Гудвин дальше совершил еще две ошибки, которые по стечению обстоятельств отменили друг друга, и пришел к чуть более точному значению π = 3.2.

_{Во-первых, он умножил на 7/10, а не на 10/7.
Во-вторых, он умножил на 4 (окружность состоит из 4 таких дуг), но не поделил на 2 (диаметр равен удвоенному радиусу).}

Сразу оговорюсь: это не единственная его ошибка вообще, а единственная очевидная ошибка в вычислениях. Непонятно, как именно переопределение π позволяет ему построить квадратуру круга. Если предположить, что это сработает, стороны получаемого квадрата будут примерно на 1% длиннее — погрешность достаточно малая, чтобы на глазок решение казалось верным.

Гудвин расхождение между его значением 3.2 и «общепризнанным» 3.1416, а потом заявляет, что 3.1416 — ошибочное. Это, на мой взгляд, самое захватывающее и жуткое в мракобесии. Даже если это что-то несусветное и легко опровергается эмпирически, их вера в собственное утверждение непоколебима. Слабые метакогнитивные способности не позволяют им даже допустить собственную неправоту. Это не он где-то допустил ошибку, а все остальные облажались. Многим мракобесам присущи иллюзии величия, они сравнивают себя с Галиллеем или Эйнштейном. Впрочем, если бы я думал, что обладаю истинным знанием о вселенной, я бы тоже сравнивал.

Идем в правительство!

Итак, у Гудвина появился способ в прямом смысле сделать невозможное. Как о нем рассказать? Конечно, его нужно опубликовать! В 1894 году он отправил свое доказательство в Американский Ежемесячный Математический Журнал (American Mathematical Monthly, AMM), который опубликовал его в июльском выпуске.

Как оно могло туда попасть? Просто повезло. AMM был основан всего за 7 месяцев до этого, и редакторы еще не определились с курсом издания. Общее направление заключалось в том, чтобы сделать математику доступнее и интереснее для широкой аудитории, и они пробовали различные способы этого добиться. Как писал один историк, в первое время они печатали «все, что присылали — или по крайней мере то, на что хватало места». Сначала они печатали «высшую пробу», а потом уже все остальное. Доказательство Гудвина было опубликовано в разделе «Запросы и информация», который редакторы не проверяли вообще.

_{Также в этом разделе постоянно творилась перепалка между авторами.}

Но тонкости внутренней работы издательства для большинства недоступны: они думают, что «опубликовано» и «признано» — одно и то же. Это дало Гудвину желаемую убедительность и раздуло его мракобесские амбиции. В 1889 году он уже оформил «копирайт» на свое доказательство, и теперь, думая, что все математическое сообщество его поддерживает, решил заработать на нем денег. Он считал, что открытие такого масштаба должны проходить в каждой школе, а значит каждая школа должна платить ему отчисления за использование его доказательства. Поэтому в 1897 году он обратился в законодательные органы штата Индиана с предложением: они официально объявят его доказательство верным, а он взамен позволит им использовать его бесплатно, что сэкономит государству кучу денег.

Так что да, мотивация правительства штата Индиана была в экономии бюджетных средств.

Закон можно прочитать целиком по этой ссылке.

Новое платье короля

Не до конца понятно, как именно постановление прошло рассмотрение. Некоторые люди спекулируют, что члены палаты представителей не обладали математической грамотностью и не поняли, что фраза «диаметр относится к длине окружности, как пять четвертых к пяти» была про число π. Мне же кажется, что поначалу они догадывались, что это брехня! Вот что пишет The Telegraph:

Гаст из Блумингтона, демократ, под громкий хохот заявил, что постановление нужно отправить в Министерство Финансов, поскольку оно взяло на себя ответственность за решение глобальных задач и обладает свободным временем. Другой представитель поднялся и высказал мнение, что более уместным окажется Министерство Болот. В такой шутливой обстановке спикер отправил «Квадратуру Круга» в Министерство Болот, где, в болоте, постановление и найдет достойную могилу.

Но потом Министерство Каналов («болот») отправило его в Министерство Образования, а оттуда оно вернулось с полной поддержкой государственного управляющего. Постановление было принято с 67 голосами «за» и без единого голоса «против». Как же так? Моя догадка: никто, по иронии, не хотел показаться глупым. Большинство людей не знакомы с мракобесием и не могут с легкостью отличить бред от фактов, которые просто звучат неправдоподобно для не разбирающегося в теме человека. Вы действительно хотите быть тем человеком, который вздумал попрепираться с Эйнштейном? По крайней мере, этого хватило, чтобы убедить газету Indianapolis Journal:

Среднестатистический редактор не добьется ничего особого, поднимая на смех открытие, признанное Американским Математическим Журналом, подтвержденное профессорами Национальной Астрономической Обсерватории Вашингтона (в том числе профессором Холлом, который открыл спутники Марса), объявленное «безупречным» профессорами из университетов Энн Арбор и Джона Хопкинса, а также запатентованное в семи странах Европы. Он едва ли настолько подкован в математике, чтобы противостоять их совместному авторитету.

Может быть, это и палату представителей тоже убедило? На мой взгляд, звучит вполне правдоподобно, но это спекуляция.

_{Гудвин утверждал, что обсудил это с Аcафом Холлом, и все поверили ему на слово. Почему именно с ним? Возможно потому, что он первым публично провел эксперимент Бюффона с бросанием иглы — это способ вычисления π с помощью случайной выборки. Могу представить, как Гудман услышал про это и решил, что Холл тоже пытается найти его истинное значение — еще один ске(π)тик.}

Какими бы ни были причины, постановление прошло, и Сенат тоже собирался его принять. Но так случилось, что на той неделе в Капитолии оказался математик из университета Purdue. Кто-то из сенаторов спросил его мнение, и ученый объяснил, почему доказательство было чушью — в результате постановление ушло в стол. Думаю, что это подтверждает мою гипотезу: мракобес может сойти за эксперта и заставить людей усомниться в себе, но когда в дело вступает настоящий эксперт, заклинание рассеивается.

Гудвин умер спустя 5 лет в возрасте 77. Многие его знакомые все еще в него верили. Из его некролога:

Годы шли, а дитя его гения оставалось непринятым математическим сообществом. Он был разбит досадой, но никогда не терял надежды на то, что доживет до момента, когда мир узрит величие его замысла, а он испытает мимолетное блаженство успеха. На фоне размеренной деревенской жизни разыгралась трагедия нереализованных амбиций.

В чем мораль этой истории? Большинство людей ограничиваются выводом о том, что американцы / жители Индианы / политики — тупицы. Я же считаю, что главное в истории — мракобесие. Оно нарушает наши эпистемологические нормы, подавая абсолютную неправоту с абсолютной самоуверенностью. Мало кто оказывается к этому готов. Гудвин, по всем меркам, обладал харизмой и говорил убедительно. Он вел себя как человек, которому можно верить — люди и верили, и от его лица чуть не развалили геометрию.

Но если не брать в расчет его почти-успех, Гудвин ничем не отличался от других мракобесов. Он думал, писал и действовал точно так же. Я иногда получаю электронную почту с таким же мракобесным настроением. Сто лет прошло, а оно ни капли не поменялось.

 

Источник