В развитии темы орнитоптеров хотелось бы рассказать, как можно решать подобные инженерные задачи с высокой степенью неопределенности результата.
И так, наш махолет является самым большим подобным аппаратом на планете. Ближайший полноценно летающий аппарат весит в 3 раза меньше. Как же двум молодым инженерам удалось создать аппарат, который многие считают невозможным? Для этого существует определенный алгоритм, который является компиляцией из классической инженерии, ТРИЗа и личного опыта.
1. Постановка задачи.
Большинство инженеров, занимающихся этой задачей, стремились повторить полет птиц или насекомых, либо изобретали некие совершенно невероятные конструкции, весьма далекие от принципов аэродинамики. Первый подход заведомо обречен на провал, так как создать адаптивное крыло подобное птичьему или насекомого крайне сложная инженерная задача, не решаемая на данном этапе развития техники. Второй подход примитивен, так как большинство предлагаемых способов создания аэродинамических сил не имеют ничего общего с законами среды.
В связи с этим мы упростили задачу и свели ее к следующему: как создавать необходимые для полета аэродинамические силы на основании существующей аэродинамической теории. Именно отталкиваясь от классической теории, глубоко ее изучив можно придумать что-то новое. Базируясь на законах дозвуковой аэродинамики нам удалось вывести уравнение полета махолета, которое описывает поле возможных скоростей и масс в которых может существовать подобный аппарат. Это позволило перейти к следующему этапу — моделированию.

2. Информационно-энергетическая модель.
Для перехода от общей теории полета к проектированию конкретного аппарата нам предстояло создать математическую модель движения сегмента крыла — бесконечного размаха по гармонической траектории. Звучит сложно, но если упростить, то идея в том, чтобы попытаться смоделировать, какими именно параметрами должно обладать крыло, чтобы создать потребные для полета силы. И тут мы использовали 2 модели:
— модель идеального крыла (это модель крыла, где каждое сечение соответствует заданным параметрам)
— модель жесткого или реального крыла.
Эти две модели стали базисом для определения поля возможных сочетаний параметров, тем самым снизив степень неопределенности решения задачи во много раз.
Сама по себе модель, это не набор формул написанных на бумажке, это математический алгоритм с широкими возможностями, который позволяет оценить диапазон используемых параметров, откорректировать существующие предположения согласно полученным экспериментальным данным.
По факту эта модель имеет следующую структуру:
— энергетическая модель – это модель взаимодействия искомых характеристик с параметрами среды
— информационная модель – модель взаимосвязи параметров друг с другом.
Такие модели были созданы не только для аэродинамики, но динамики и конструкции.
Фактически это своеобразная «машина времени», которая позволяет прибывать одновременно на всех стадиях проекта. Тем самым вся задача сводится к тому, то через совершенствование модели вы начинаете совершать предсказания по поведению реальной модели-прототипа.
Чем больше вы получаете экспериментальных данных тем точнее и лучше предсказание.
Подобная динамическая модель и позволила нам довести модель полета.
3. Опыт и аналитика.
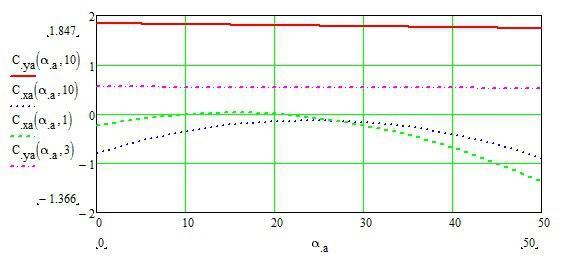
Самой большой загадкой махолета является его аэродинамика. Так как в ходе опыта мы выявили значительные расхождения между классической теорией и результатами испытаний.
Аэродинамика махолета крайне сложная для понимания и описания вещь. Проще говоря — не понятно, как он вообще летает.
И вот в чем дело:
Если мы с вами рассмотрим идеальное крыло (крыло птицы, как эталон), то оно способно в каждом своем сечении обладать своими оптимальными характеристиками, что им и позволяет весьма эффективно расходовать энергию.
Но если мы возьмем жесткие крылья, как на нашей модели, то вот тут начинается веселье. Большая часть крыла находится в зоне срыва потока, что с энергетической точки зрения крайне не выгодно (высокое сопротивление и малая подъемная сила), но если мы посмотрим на реальные характеристики полета (прямые замеры тяги и подъемной силы), то окажется что средние по времени показатели подъемной силы и тяги весьма приемлемы (аэродинамическое качество 10-12). Отчего так?
Вот тут начинается совсем другая аэродинамика. Видите ли, вся современная авиационная наука стоит на базисе, что аэродинамическая плоскость находится в равноускоренном или равномерном потоке и значения аэродинамических коэффициентов весьма стабильны. Но вот если теперь мы возьмем не равноускоренное движение, то воздух начинает проявлять себя совсем иначе, проявляется эффект присоединенных масс. Что это за эффект? Присоединенные массы это условные массы присваиваемые движущемуся объекту, что бы скорректировать его динамические свойства при движении в вязкой среде. Однако мне кажется, что данное явление можно рассматривать и иначе, что воздух, как и вода способны проявлять свойства условного повышения вязкости при ускоренном движении. Т.е. воздух ведет себя как неньютоновская жидкость, только она не становится «твердой», а становится более упругой.
Данное явление может нам раскрыть совсем другое направление аэродинамики, которое на текущий момент мало изучено (только в области маха лопасти вертолета). В нем могут крыться секреты повышения аэродинамических характеристик существующих ЛА и создание принципиально новых способов полета, вроде машущего.

Именно строго научный подход и создание соответствующего математического аппарата, а так же много-много часов устранения недостатков конструкции позволили нам реализовать полет.
По факту этот алгоритм применим к абсолютно любой инженерной задачи связанной с созданием принципиально новых вещей.
И так, наш махолет является самым большим подобным аппаратом на планете. Ближайший полноценно летающий аппарат весит в 3 раза меньше. Как же двум молодым инженерам удалось создать аппарат, который многие считают невозможным? Для этого существует определенный алгоритм, который является компиляцией из классической инженерии, ТРИЗа и личного опыта.
1. Постановка задачи.
Большинство инженеров, занимающихся этой задачей, стремились повторить полет птиц или насекомых, либо изобретали некие совершенно невероятные конструкции, весьма далекие от принципов аэродинамики. Первый подход заведомо обречен на провал, так как создать адаптивное крыло подобное птичьему или насекомого крайне сложная инженерная задача, не решаемая на данном этапе развития техники. Второй подход примитивен, так как большинство предлагаемых способов создания аэродинамических сил не имеют ничего общего с законами среды.
В связи с этим мы упростили задачу и свели ее к следующему: как создавать необходимые для полета аэродинамические силы на основании существующей аэродинамической теории. Именно отталкиваясь от классической теории, глубоко ее изучив можно придумать что-то новое. Базируясь на законах дозвуковой аэродинамики нам удалось вывести уравнение полета махолета, которое описывает поле возможных скоростей и масс в которых может существовать подобный аппарат. Это позволило перейти к следующему этапу — моделированию.

2. Информационно-энергетическая модель.
Для перехода от общей теории полета к проектированию конкретного аппарата нам предстояло создать математическую модель движения сегмента крыла — бесконечного размаха по гармонической траектории. Звучит сложно, но если упростить, то идея в том, чтобы попытаться смоделировать, какими именно параметрами должно обладать крыло, чтобы создать потребные для полета силы. И тут мы использовали 2 модели:
— модель идеального крыла (это модель крыла, где каждое сечение соответствует заданным параметрам)
— модель жесткого или реального крыла.
Эти две модели стали базисом для определения поля возможных сочетаний параметров, тем самым снизив степень неопределенности решения задачи во много раз.
Сама по себе модель, это не набор формул написанных на бумажке, это математический алгоритм с широкими возможностями, который позволяет оценить диапазон используемых параметров, откорректировать существующие предположения согласно полученным экспериментальным данным.
По факту эта модель имеет следующую структуру:
— энергетическая модель – это модель взаимодействия искомых характеристик с параметрами среды
— информационная модель – модель взаимосвязи параметров друг с другом.
Такие модели были созданы не только для аэродинамики, но динамики и конструкции.
Фактически это своеобразная «машина времени», которая позволяет прибывать одновременно на всех стадиях проекта. Тем самым вся задача сводится к тому, то через совершенствование модели вы начинаете совершать предсказания по поведению реальной модели-прототипа.
Чем больше вы получаете экспериментальных данных тем точнее и лучше предсказание.
Подобная динамическая модель и позволила нам довести модель полета.

3. Опыт и аналитика.
Самой большой загадкой махолета является его аэродинамика. Так как в ходе опыта мы выявили значительные расхождения между классической теорией и результатами испытаний.
Аэродинамика махолета крайне сложная для понимания и описания вещь. Проще говоря — не понятно, как он вообще летает.
И вот в чем дело:
Если мы с вами рассмотрим идеальное крыло (крыло птицы, как эталон), то оно способно в каждом своем сечении обладать своими оптимальными характеристиками, что им и позволяет весьма эффективно расходовать энергию.
Но если мы возьмем жесткие крылья, как на нашей модели, то вот тут начинается веселье. Большая часть крыла находится в зоне срыва потока, что с энергетической точки зрения крайне не выгодно (высокое сопротивление и малая подъемная сила), но если мы посмотрим на реальные характеристики полета (прямые замеры тяги и подъемной силы), то окажется что средние по времени показатели подъемной силы и тяги весьма приемлемы (аэродинамическое качество 10-12). Отчего так?
Вот тут начинается совсем другая аэродинамика. Видите ли, вся современная авиационная наука стоит на базисе, что аэродинамическая плоскость находится в равноускоренном или равномерном потоке и значения аэродинамических коэффициентов весьма стабильны. Но вот если теперь мы возьмем не равноускоренное движение, то воздух начинает проявлять себя совсем иначе, проявляется эффект присоединенных масс. Что это за эффект? Присоединенные массы это условные массы присваиваемые движущемуся объекту, что бы скорректировать его динамические свойства при движении в вязкой среде. Однако мне кажется, что данное явление можно рассматривать и иначе, что воздух, как и вода способны проявлять свойства условного повышения вязкости при ускоренном движении. Т.е. воздух ведет себя как неньютоновская жидкость, только она не становится «твердой», а становится более упругой.
Данное явление может нам раскрыть совсем другое направление аэродинамики, которое на текущий момент мало изучено (только в области маха лопасти вертолета). В нем могут крыться секреты повышения аэродинамических характеристик существующих ЛА и создание принципиально новых способов полета, вроде машущего.

Именно строго научный подход и создание соответствующего математического аппарата, а так же много-много часов устранения недостатков конструкции позволили нам реализовать полет.
По факту этот алгоритм применим к абсолютно любой инженерной задачи связанной с созданием принципиально новых вещей.
Источник

