Радиокоммуникации играют ключевую роль в современной электронике, но их теорию сложно понять начинающему любителю. Да, у нас есть общее представление: мы знаем о частотах и, вероятно, можем объяснить разницу между амплитудной и частотной модуляциями. Однако большинству из нас сложно сформулировать, как создать качественную антенну или как приёмник может настраиваться на конкретную частоту, игнорируя все остальные.
В этой статье я постараюсь изложить введение в радио без использования жаргона радиолюбителей и сложной математики. Для этого я воспользуюсь концепциями, рассмотренными в четырёх предыдущих статьях моего блога:
- Базовые концепции электронных цепей
- Электромагнитные поля и хранение энергии
- Задержки распространения сигналов и отражения сигналов
- Анализ диапазона частот при помощи дискретного преобразования Фурье и дискретного косинусного преобразования
Если вы подзабыли какие-то из этих тем, то рекомендую сначала освежить память.
▍ Давайте изготовим антенну
Если вы знакомы с основами электроники, то проще всего начать изучение антенн, представив заряженный конденсатор, растягиваемый так, что его внутреннее электрическое поле распространяется по окружающему пространству:
 Превращаем конденсатор в ужасную антенну
Превращаем конденсатор в ужасную антенну
Электрические поля можно визуализировать, отрисовав пути гипотетических положительно заряженных частиц, расположенных по соседству. В случае нашего бывшего конденсатора мы увидели бы дугообразные линии, соединяющие пластины (строго говоря, они распространяются в обе стороны в бесконечность).
Неизменяющееся электрическое поле не особо полезно для радио, но если мы начнём перемещать заряды туда и обратно между полюсами антенны, то получим замечательный релятивистский эффект: цепочку переменных полей, распространяющуюся со скоростью света, ускользая с частью энергии, которую мы раньше всегда могли вернуть из статического поля конденсатора.
Иными словами, поприветствуйте электромагнитные волны:
Идеально ровный сигнал тоже бесполезен для коммуникаций, но мы можем закодировать информацию, слегка меняя его характеристики, например, регулируя амплитуду. И если мы так поступим, то благодаря хитрому трюку, о котором мы поговорим чуть ниже, принимающей стороне можно разделять одновременные передачи на разных частотах.
Но для начала нужно провести проверку: если мы подключим наш разобранный конденсатор к источнику сигнала, то ничего не произойдёт. Разделив пластины, мы существенно снизили электроёмкость устройства, то есть, по сути, получили разомкнутую цепь. Для перемещения достаточного количества электронов потребуется довольно высокое напряжение. Без этого движения, то есть без надёжного тока, излучаемая энергия будет ничтожной.
Самое изящное решение этой проблемы заключается в использовании полуволновой дипольной антенны: два проводника на одной оси, на которые из центра подаётся синусоидальный сигнал, а длина каждого проводника равна ¼ длины волны. Если вы забыли или не знали, преобразование из частоты (f, в герцах) в длину волны (λ) выполняется по следующей формуле:
Третье значение (c) — это скорость света за секунду в предпочтительных единицах измерения.
Полуволновой диполь имеет интересное свойство: если мы примем в расчёт задержки распространения сигнала, то увидим, что каждый пик ведущего сигнала достигает концов антенны идеально синхронно с предыдущим колебанием. Такой паттерн приводит к созданию стоячей волны с существенным размахом напряжения на дальних концах антенны. Ещё одна особенность заключается в постоянно низком напряжении (и низком импедансе) в точке возбуждения. Благодаря всем этим характеристикам антенна оказывается очень эффективной и удобной в управлении:
Все диполи, рассчитанные на нечётные кратные полуволн (3/2 λ, 5/2 λ, …), проявляют такое резонирующее поведение. Похожий резонанс также присутствует в чётных кратных (1 λ, 2 λ, …), но стоячая волна оказывается не в том месте, постоянно мешая возбуждению антенны, а не помогая ему.
Антенны с другими длинами резонируют неидеально, но могут быть достаточно близки. Слишком короткую для резонанса антенну можно улучшить подключением коллинеарного индуктора, добавляющего отставание тока. Возможно, вы видели антенны с пружинообразными секциями в основании — это называется электрическим удлинением. При этом характеристики короткой антенны будут не такими же, как у обычной, но это позволяет контролировать входное полное сопротивление.
Рассмотрев в общем полуволновые диполи, давайте вернёмся к анимации распространения поля антенны:
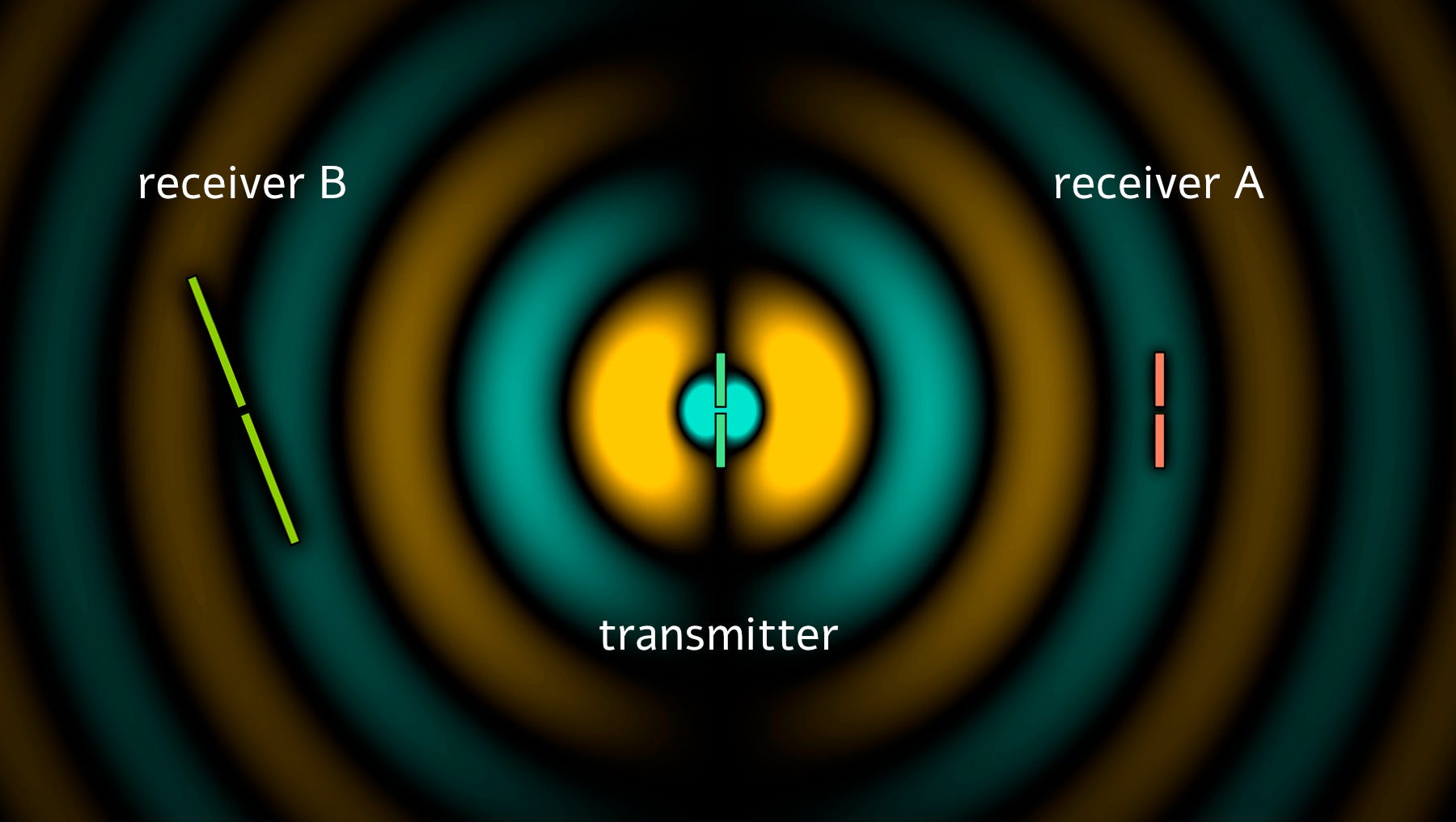
Обратите внимание на две мёртвые зоны вдоль оси антенны — они возникают из-за деструктивной интерференции электрических полей. Посмотрим, сможете ли сами понять причину — помните, что для прохождения по всей длине диполя сигналу нужна ровно половина цикла.
Теперь давайте подумаем, что произойдёт, если мы расположим идентичную принимающую антенну на каком-то расстоянии от передатчика. Посмотрите на приёмник A справа:

Легко увидеть, что красный диполь «плывёт» в переменных электрических полях — он «ощущает» между своими полюсами возвратно-поступательные токи на рабочей частоте передатчика. Кроме того, если длина антенны подобрана правильно, должна также возникать конструктивная интерференция индуцированных токов, что приводит к гораздо большим амплитудам сигнала.
На иллюстрации показано интуитивно понятное объяснение того, о чём я не говорил выше: что диполи длиннее ½ длины волны более направленные. Если посмотреть на приёмник B слева, то станет ясно, что даже небольшой наклон длинного диполя приводит к тому, что концы подвергаются действию противоположных электрических полей, приводя к сильному снижению или полному отсутствию суммарного тока.
Не все антенны являются диполями, но большинство работает схожим образом. Одним из небольших отличий монополя является то, что одна половина антенны заменена на подключение к земле. Более сложные формы обычно используются с целью поддержания резонанса на множественных частотах или для тонкой настройки направленности. Вы можете столкнуться и с антенными решётками — эти устройства используют паттерны конструктивной и деструктивной интерференции между сигналов с цифровым управлением для гибкой фокусировки на нужной точке.
▍ Преимущества и недостатки модуляции сигналов
В сравнении с конструкцией антенн модуляция сигнала выглядит гораздо проще. Существует амплитудная модуляция (AM), меняющая амплитуду несущего сигнала для кодирования информации; есть частотная модуляция (frequency modulation, FM), сдвигающая несущий сигнал вверх и вниз; и есть фазовая модуляция (phase modulation, PM). Также существует квадратурная амплитудная модуляция (quadrature amplitude modulation, QAM), которая надёжным образом передаёт информацию при помощи относительной амплитуды двух сигналов с фазами, смещёнными на 90°.
Как бы то ни было, после выделения несущего сигнала демодуляцию обычно выполнить довольно легко. В случае AM бывает достаточно очистить усиленную синусоиду при помощи диода, а затем пропустить её через фильтр низких частот, чтобы получить огибающую звуковой частоты. С другими модуляциями всё чуть сложнее, в FM и PM для определения сдвигов используются фазовая автоподстройка частоты, но в целом в этом нет ничего особенно сложного.
Однако в модуляции всё равно есть два тонких момента. Во-первых, частота изменения несущего сигнала должна быть гораздо меньше, чем его рабочая частота. Если модуляция слишком быстрая, то несущая волна будет уничтожена и превратится в широкополосный шум. Единственная причина работы цепей резонансных антенн и настройки радио заключается в том, что между циклами практически ничего не меняется, так что при локальном отслеживании мы имеем дело с почти идеальной синусоидой постоянной частоты.
Второй аспект заключается в том, что вся модуляция является частотной. Может показаться, что AM — это какой-то хитрый фокус с нулевой шириной полосы: в конечном итоге, мы просто меняем амплитуду синусоиды фиксированной частоты, так что может помешать нам выполнять любое количество AM-передач, разделённых на небольшую часть герца?
К сожалению, это невозможно: в посте о преобразовании Фурье мы говорили, что любое отклонение от стабильной синусоиды привносит в диапазон частот кратковременные артефакты. Масштаб артефактов пропорционален частоте изменения — AM в этом не уникальна и тоже занимает полосу частот. Проиллюстрируем это сигналом местной AM-станции. Как видно, артефакты модуляции звука распределяются на несколько кГц по обе стороны от несущей частоты:

И в самом деле, все типы модуляции сводятся к тому, что берётся низкочастотный диапазон сигналов (например, звук) и тем или иным образом перемещается в срез спектра схожего размера в окрестностях какой-то выбранной центральной частоты.
Здесь кто-то может возразить: преобразование Фурье — не единственный способ восприятия спектра частот. Только то, что мы видим гало на графике быстрого преобразования Фурье, не значит, что они на самом деле реальны. Теоретически это может быть правдой. Но дело в том, что принцип работы радиоприёмников очень напоминает преобразование Фурье…
▍ Внутри супергетеродинного приёмника
Как мы сказали чуть выше, принцип работы почти каждого радиоприёмника сводится к смешению (умножению) усиленного сигнала антенны с синусоидой выбранной частоты. Это очень похоже на то, как преобразование Фурье разделяет сложные сигналы на отдельные частотные компоненты.
В обсуждении дискретного косинусного преобразования (DCT) в одной из предыдущих статей говорилось, что если совпадающая частота присутствует во входном сигнале, то при умножении получается волна с постоянным смещением, пропорциональным величине этого частотного компонента. Для всех остальных входных частот получающиеся волны при анализе в течение достаточно долгого промежутка времени обнуляются.
Но этот временной промежуток усреднения тоже любопытен: в вышеупомянутой статье мы отметили, что итоговые составные колебания имеют более короткие периоды, если исходные частоты находятся далеко друг от друга, и более длинные, если частоты близки. Как оказывается, для DCT низкочастотный цикл всегда имеет вид |f1 — f2| и наложен поверх менее интересного высокочастотного цикла.

Это поведение может показаться загадочным, но оно естественным образом возникает из свойств синусоид. Давайте начнём с равенства сумм углов, имеющего красивое и простое доказательство на основе треугольников. Это равенство имеет следующую формулу:
Из этого можно тривиальным образом показать следующее:
Если поделить обе части пополам и перевернуть, то мы получим формулу равенства произведения двух частот синусоид и суммы косинусов при f1 — f2 и f1 + f2:
Для доказательства нам даже не нужно верить в тригонометрию. Музыкантам уже давно известно тесно связанное с этим явление: при воспроизведении двух очень схожих тонов в результате получается неожиданная медленно пульсирующая частота. Вот демонстрация пульсации в 5 Гц, создаваемая сочетанием 400 Гц и 405 Гц:
Впрочем, вернёмся к радио: из этого следует, что если нам нужно получать передачи, центрированные относительно 10 МГц, то проще всего будет смешать входной радиосигнал с синусоидой на 10 МГц. Согласно нашим формулам, это должно понизить частоту 10,01 МГц до пульсации в 10 кГц (с дополнительным компонентом 20,01 МГц), превратить 10,02 МГц в 20 кГц (+ 20,02 МГц) и так далее. После завершения смешения на выходе применяется фильтр низких частот, сохраняющий только низкие частоты, составляющие схему модуляции, и избавляющий от всего ненужного, в том числе от нежелательных компонентов f1 + f2. Недостаток этой методики становится очевидным, если вспомнить, что на выходе частоты пульсации проявляют симметрию относительно 0 Гц. В вышеупомянутом примере входной компонент 9,99 МГц создаёт зеркальный сигнал на 10 кГц — именно там, где должны были оказаться 10,01 МГц. Чтобы избежать этого отзеркаливания, приёмники смешивают радиочастотный входной сигнал с частотой ниже, чем интересующий нас сигнал, сдвигая его на постоянную ненулевую промежуточную частоту (fif), а затем применяют полосовой фильтр для извлечения соответствующих частей.
В такой схеме, придуманной Эдвином Армстронгом примерно в 1919 и названной супергетеродином, по-прежнему присутствует неотъемлемое отзеркаливание, но точка симметрии может быть размещена очень далеко. Благодаря этому трюку становится проще управлять случайным отзеркаливанием ненужных нам передач, например, спроектировав антенну так, чтобы она имела узкую частотную характеристику и вообще не принимала мешающие сигналы, или разместив перед смесителем фильтр низких радиочастот. Поведение супергетеродинов иногда принимается во внимание и при выделении спектра радиочастот.
Telegram-канал со скидками, розыгрышами призов и новостями IT 💻



