Как Осборн Рейнольдс пришёл к своему числу. Часть 3

II Эксперименты с цветными полосками в стеклянных трубках.

18.

Когда эти эксперименты начинались, было совершенно не понятно, при какой скорости в данной трубке будут появляться вихри. В экспериментах Пуазейля линейная зависимость сопротивления от скорости нарушалась для каналов диаметром, скажем, 0.6 мм. По данным Дарси этот закон не работал в канале диаметром 12.2 мм при скорости 152 мм/с.

Исходя из этого, а также из того, что их было сравнительно легко провести, я начал с экспериментов в маленькой трубке, рассчитывая, что в ней вихри будут видны невооружённым взглядом, и при тех скоростях, которые можно было легко реализовать.

19. Первая установка.

Она представляла собой трубку диаметром около 6 мм, согнутую в виде сифона с коленами длиной 0.6 и 1.5 м.

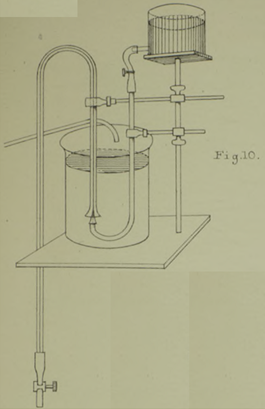
Короткое колено заканчивалось воронкой, а длинное – резиновой насадкой с краном. Короткое колено располагалось вертикально посредине чаши, воронка находилась в нескольких сантиметрах от её дна.

Трубка с подкрашенной водой диаметром 6 мм тоже была в виде сифона. Как показано на рисунке, короткое колено с открытым концом находилось под воронкой. Длинное колено через кран соединялось с ёмкостью, в которой находилась сильно подкрашенная вода. Эта ёмкость устанавливалась на достаточной высоте. Ещё одна трубка служила просто для наполнения чаши водой. При этом не предполагалось поддерживать чашу целиком заполненной, так как втекающая вода создавала бы слишком большие возмущения. Опыт показал, что для таких экспериментов важно дать воде сначала полностью устаканиться.

20. Первый эксперимент.

Ёмкости и сифоны были наполнены и стояли несколько часов, чтобы всякое внутреннее движение прекратилось. Затем открыли кран с подкрашенной водой, и она начала медленно вытекать под воронку, как на рисунке 11.

Далее очень медленно стали открывать кран на сифоне с воронкой. Вода стала затекать в неё, при этом подкрашенная вода сначала выглядела как пламя свечи (рисунок 12), затем постепенно вытягивалась, и превращалась в  очень тонкую полоску.

Как показано на рисунке 10′, полоска начинала сжиматься сразу на выходе из цветной трубки, и продолжалась от воронки до самого выходного отверстия.

Если сильнее открыть нижний кран, то  скорость потока увеличивалась, а расход краски не менялся, при этом полоска становилась тоньше. Далее, чтобы увеличить её толщину, увеличивали расход краски. Так продолжалось до достижения максимальной скорости в этих условиях, то есть до полного открытия нижнего крана. Даже в этом случае на всём протяжении канала была чётко видна полоска. Очевидно, для появления вихрей нужна была боль`шая скорость. Для этого длинное колено было удлинено ещё на 0.6 метра, и стало доставать до пола.

Однако и после этой модификации полоска по-прежнему оставалась чёткой и невозмущённой.

В итоге за неимением возможности достичь более высоких скоростей, в этом эксперименте вихри не обнаружились.

Подача воды во время эксперимента приводила к возмущению воды в чаше. Это в свою очередь несколько возмущало полоску, однако трудно сказать, были ли это колебания самой полоски или проявление  вихрей.

21. Окончательный вариант установки.

В окончательном виде установка стала значительно больше. Из широкого ассортимента трубок была выбрана наиболее ровная, с непостоянством диаметра не более 0.7 мм при диаметре около 25 мм и длине 1.5 м.

Трубка была установлена горизонтально. На один конец, который на вид казался несколько бо`льшим, была установлена воронка из лакированного дерева. Большое внимание уделено тому, чтобы стекло и дерево были заподлицо. Другой конец через резиновую шайбу соединялся с железной трубкой диаметром около 2 дюймов (51 мм).

Из торца бака горизонтально выходила железная трубка. Длина бака 1.8 метра, ширина и глубина 0.46 метра. На выходе из бака она сгибалась на 90 градусов и вертикально опускалась на уровень 2.1 метра ниже, чем стеклянная трубка. На конце был уставлен большой кран, который в полностью открытом состоянии обеспечивал проходное сечение около квадратного дюйма (645 квадратных миллиметров).

Кран управлялся длинным рычагом, который доходил до высоты, на которой находился бак, т.е. 2.1 метра от пола. На высоте  1.2 метра от пола вокруг бака была сооружена площадка для наблюдения. Стеклянная трубка проходила горизонтально посредине бака, а воронка находилась на расстоянии чуть менее 0.3 метра от торца бака. Через этот торец, напротив воронки, была подведена цветная трубка диаметром 19 мм. Через резиновую трубку с краном она соединялась с бутылкой с подкрашенной водой.

Скорость потока измерялась с помощью приспособления, которое позволяло измерять уровня воды с точностью 0.25 мм. На нескольких высотах в баке были подвешены термопары.

22. Чистовые эксперименты.

Первый эксперимент на этой установке был проведён 22-го февраля 1880-го года.

Бак был заполнен с помощью водопроводной магистрали и шланга и оставлен на несколько часов, с 10:00 до 14:00. После этого температура воды была 46°F (25.6°C) у дна и 47°F (26.1°C) у поверхности. Эксперимент был начат так же, как в первом варианте. Кран был слегка приоткрыт, и краска медленно потекла. Струйка краски так же, как и ранее, была красивой и устойчивой. Скорость постепенно увеличивалась за счёт медленного открытия крана, и в какой-то момент на расстоянии 0.6 м от железной трубки полоска расширилась и перемешалась с водой, закрасив остаток канала облаком  равномерного цвета на первый взгляд.

Однако если проследить движение воды глазом, было хорошо видно, что расширение полоски происходит в результате волнового движения. Сначала оно не испытывает возмущений, но после двух-трёх волн появляются чётко различимые отдельные вихри. Их хорошо видно глазом, но ещё лучше в свете вспышки.

Они появились при скорости падения уровня воды 1 дюйм (25.4 мм) в минуту, что соответствует скорости потока 0.627 м/c. Если же немного прикрыть кран, вихри исчезали, и полоска снова становилась прямой.

Таким образом, мы установили существование вихрей, и то, что они появляются при определённом значении скорости. Обратимся к связи между критической скоростью, размером трубки и вязкостью.

Были подготовлены ещё две трубки (№ 2 и 3) той же длины и диаметром около 12 и 6 мм. Устанавливались они так же, как и первая трубка.

Между тем мы попробовали проследить влияние вязкости, используя воду различной температуры. Водопроводная вода имела температуру 25°C, тогда как в комнате было 30°C. Чтобы поднять температуру ещё выше, бак был разогрет до 39°C струёй пара. После этого, при насколько можно судить, тех же возмущениях, были проведены эксперименты, обозначенные в таблице 1 под номерами 1 и 2.

Для определения вязкости можно было бы использовать данные Пуазейля, но были опасения из-за возможных отличий в свойствах исследуемой воды. Поэтому мы повторили эксперименты Пуазейля для нашей воды из бака, и их результаты очень хорошо совпали с его данными. Поэтому для вязкости можно использовать его формулу P^-1 = 1 + 0.03368T + 0.00021T², где P~μ с изменением температуры, а T – в градусах Цельсия.

Значения P при 26 и 39°C относятся как 1.3936 к 1, а значения критических скоростей при этих температурах относятся как 1.45 к 1. Это очень хорошее совпадение с учётом погрешностей экспериментов.

Однако что бы ни было причиной аномалий, которые наблюдались ранее, в подогретом баке их стало ещё больше. После подогрева бак час или два устаканивался. После открытия крана наблюдались вихри, однако они были не похожи на вихри в холодной воде. Видимо, причиной этому был какой-то источник начальных возмущений. Например, то, что температура бака была на 11°C выше комнатной, должно было приводить к охлаждению воды у поверхности и у стенок бака, что в свою очередь должно было вызывать в воде циркуляцию. Подкрашенные полоски, добавленные в воду, это подтвердили, хотя циркуляция была очень медленной. Ещё один источник возмущений – разница в температуре 2.8°C между верхом и низом бака.

Для устранения этих возмущений нужно было иметь температуру бака как в комнате, около 30°C. Тогда по результатам нескольких измерений получилось, что вихри возникают при скорости падения уровня воды около 1 дюйм за 64 секунды, что, с учётом вязкости, больше, чем в предыдущем случае. Видимо, это обусловлено тем, что в воде было меньше возмущений.

Итак, чтобы провести эксперименты при повышенной температуре и при прочих равных, нужно было изменить температуру в здании, что представлялось сложным. Однако, той же цели можно было достигнуть, охладив воду с помощью льда до её максимальной плотности при 22 °C.

Были проведены эксперименты с тремя трубками 1, 2 и 3 при температурах около 28 и 22 °C. Результаты приведены в таблице 1.

Таблица 1. Эксперименты с цветными полосками – критические скорости распада устойчивого движения.

Трубка №1	стекло	диаметр 0.0268 м	log. диаметра 2.42828
Трубка №2	стекло	0.01527	2.18400
Трубка №3	стекло	0.007886	3.89783

Расход 0.021237 куб. м; log = 2.32709.

Дата, 1880	№ п/п	Трубка	Температура, °С	Время истечения	Скорость, метры	log времени.	-log P.	log V.	log Bs.
1 марта	1	1	8.3	60	0.6270	1.77815	0.11242	1.79729	1.66200

От переводчика: остаток таблицы с численными данными можно найти в первоисточнике.

При обработке результатов длина измерялась в метрах, температура – в градусах Цельсия.

Диаметры трубок были определены путём заполнения их водой.

Время истечения – это время, за которое уровень воды в баке падал на 1 дюйм (25.4 мм), что соответствует объёму Q = .021237 м³.

В таблице приведены значения P, V и B_s, а также их логарифмы.

Скорость получена по формуле .

получено по формуле .

Итоговое значение = 43.79 получено из среднего значения логарифма =1.64139.

23. Результаты.

Полученные значения log B_s практически одинаковы. Это доказывает, что существует критическая скорость, при которой начинают появляться вихри, и что она пропорциональна вязкости и обратно пропорциональна диаметру трубки.

Но не будем забывать, что это соотношение получено лишь после большой работы по минимизации уровня внутренних возмущений в воде.

Тот факт, что устойчивое движение распадается внезапно, означает, что жидкость неустойчива к возмущениям с достаточно большой амплитудой. То, что при определённых условиях оно распадается от большого возмущения, но устойчиво к меньшим возмущениям, означает, что пока возмущение не превышает некоторого уровня, существует некоторая остаточная устойчивость.

Единственная гипотеза, которую я выработал перед началом экспериментов, заключалась в том, что при некоторой критической скорости движение становится неустойчивым, и при любом отклонении от идеально устойчивого движения возникают вихри.

Я не имел представления о том, какой именно вид возмущений необходим. Практика показывала, что абсолютно устойчивое движение невозможно, поэтому я не сомневался, что появление вихрей происходит почти одновременно с потерей устойчивости. Поэтому я старался максимально подавить возмущения. Я ожидал, что с увеличением скорости вихри будут сначала появляться медленно и вяло, так как сначала неустойчивость воды слаба. Поэтому была полной неожиданностью та внезапная сила, с которой возникают вихри, которая указывает на то, что сильная неустойчивость возникает сразу в момент распада устойчивого движения.

Это привело меня к мысли о том, что возмущения определённой амплитуды приводят к неустойчивости, а более слабые возмущения устойчивы.

Для исследования этого я внёс в поток искусственное возмущение, установив проволочную спираль.

Теперь вихри появлялись при скорости, более чем в 2 раза меньшей, чем ранее. Они разрушали цветную полоску, но трудно было сказать, является ли движение неустойчивым, или вихри появляются из исходного возмущения. Потому что когда полоска разрушается, она перемешивается с остальной водой, и если ниже по потоку течение становится устойчивым, этого уже нельзя увидеть.

Однако дальнейшие эксперименты показали, что критическая скорость в какой-то степени зависит от того, насколько изначально вода успела устаканиться. Например, следующее явление очень показательно.

Если изначально в воде имеется значительное возмущение, и открывать кран очень медленно, то цветная полоска в трубке начинает колебаться. В этом случае она даже может попадать на стекло и растекаться, но вихрей при этом нет. Если немного увеличить скорость, то ближе к концу трубки появляются вихри, часто регулярные. При ещё большем открытии крана они исчезают, и полоска выпрямляется и фиксируется посередине трубки. В этом состоянии она находится, пока скорость не достигнет своего обычного критического значения, и вихри начнут появляться внезапно.

Ещё одно важное явление, которое особенно часто наблюдалось в маленьких трубках – перемежающийся характер возмущения. Возмущение внезапно появляется в каком-то месте трубки, сносится по течению, и появляется новое возмущение, зачастую в том же месте.  То есть они возникают как бы в виде вспышек. На рисунке 16 показан случай, когда эти вспышки возникают достаточно быстро.

Этот феномен наблюдался как для очень спокойной воды, так и при наличии начальных возмущений.

Возмущения никогда не наблюдались ближе, чем 30 диаметров от входа в трубку. Вспышки тоже обычно возникали на этом расстоянии, хотя и не всегда.

В маленьких трубках (а также в больших трубках с водой, охлаждённой до 22 °C), как правило, неустойчивость сначала проявлялась как случайная вспышка в обычном месте, которая ниже по течению превращалась в пятно длиной 50–75 мм. С увеличением скорости вспышки учащаются, и возмущение становится непрерывным.

Я не видел способа проверить утверждение, что движение становится неустойчивым для больших возмущений раньше, чем для маленьких. Но по моим впечатлениям, это в некотором роде так – как будто для возникновения неустойчивости необходимы возмущения в баке или неоднородности в трубке.

Однако, что бы ни значили эти нюансы проявлений вихрей, можно считать точно установленным тот факт, что устойчивое движение становится неустойчивым при определённом значении скорости, которое пропорционально  μ/(ρc), где c – диаметр трубки, μ/ρ – отношение вязкости к плотности. Для стеклянных цилиндрических каналов и малого уровня начальных возмущений в воде это значение составляет v = P/(B_sD), где B_s = 43.79 в метрах.

Продолжение следует.

 

Источник