Как графы помогут создать идеальный шифр

Чтобы создать оптимальный метод кодирования информации, исследователи разработали граф, который формой напоминает паутины раскрытых книг. На его базе создали локально тестируемый код, который сразу же обнаруживает ошибки, возникшие при его передаче.

Предположим, вы пытаетесь передать сообщение. Преобразуйте каждый символ в бит и каждый бит в сигнал. Затем отправьте его по медному проводу, оптоволокну или воздуху. Как бы вы ни осторожничали, принятые на другой стороне данные будут отличаться от тех, что вы послали. Шум вмешивается в работу всегда.

В 1940-х годах учёные впервые столкнулись с неизбежной проблемой шума. Пять десятилетий спустя они придумали, как его обойти. Что, если закодировать сообщение так, чтобы искажение было очевидно получателю ещё до чтения? Книгу нельзя оценить по обложке, а это сообщение — можно.

Учёные назвали это свойство локальной тестируемостью, потому что такое сообщение можно проверить всего в нескольких точках, чтобы убедиться в его точности. В течение следующих 30 лет исследователи шли к созданию такого теста, но их усилия всегда терпели неудачу. Многие думали, что идеальная локальная тестируемость невозможна.

8 ноября информатик Ирит Динур из Института Вейцмана и четыре математика, Шай Эвра, Рон Ливне, Алекс Любоцки и Шахар Мозес — все из Еврейского университета в Иерусалиме, создали такой тест и опубликовали препринт.

«Это одно из самых замечательных явлений в математике и информатике, о которых я знаю», — сказал Том Гур из Уорикского университета. «Это был святой Грааль целой отрасли».

Новый метод преобразует сообщение в суперканарейку: объект, который говорит о своём здоровье точнее, чем любое другое известное сообщение. Любое существенное искажение, которое зарыто где-нибудь в надстройке, становится очевидным после простых тестов в нескольких местах.

Большинство предшествующих методов кодирования данных полагались на случайность. Но для локальной проверки случайность не подходит. Исследователям пришлось изобрести совершенно новую структуру графа с высокой степенью неслучайности, на которой они построили свой метод. Это прогресс в обеспечении максимальной устойчивости информации.

Кодирование 101

В коммуникации повсюду присутствует шум. Исследователи сначала представляют информацию в виде последовательности битов — единиц и нулей. Шум можно назвать случайным влиянием, которое переворачивает определённые биты.

Есть много методов борьбы с этим шумом. Рассмотрим короткое и простое сообщение 01. Измените его, повторяя каждую часть — каждый бит — три раза, чтобы получить 000111. Затем, даже если шум повредит, допустим, второй и шестой биты и сообщение изменится на 010110, получатель всё ещё сможет исправить ошибки после проверки. Получатель знает, что первые три бита в сообщении кодируют один бит, вторые три бита — другой бит. Дважды получив большинство голосов — один раз для 0, один раз для 1 — пользователь приходит к содержанию сообщения 01.

Такой метод изменения сообщения называется кодом. Когда код содержит в себе процедуру исправления ошибок, он называется корректирующим. Коды похожи на словари, каждый из которых определяет набор кодовых слов, например, 000111.

Для хорошей работы код должен иметь несколько свойств. 

• Во-первых, кодовые слова в нём не должны быть слишком похожими. Если код содержит кодовые слова 0000 и 0001, потребуется всего лишь один переворот битов, чтобы спутать эти два слова. 

• Во-вторых, кодовые слова не должны быть слишком длинными. Повторяющиеся биты могут сделать сообщение более надёжным, но они также увеличивают время отправки.

Эти два свойства называются расстоянием и скоростью. Хороший код должен иметь как большое расстояние между отдельными кодовыми словами, так и высокую скорость  передачи реальной информации. Но как соединить эти свойства?

В 1948 году Клод Элвуд Шеннон показал, что случайно выбранное кодирование приближается к оптимальному компромиссу между двумя свойствами. Однако разобрать код, в котором кодовые слова выбраны наугад, чрезвычайно трудно. То есть Шеннон показал, что хорошие коды существуют, но предложенный метод их создания не работает.

В течение следующих 40 лет учёные работали, чтобы найти неслучайные шаблоны расположения битов, близкие к случайному идеалу. В 1990 году исследователи сформулировали идею локальной проверяемости. Локально проверяемые коды были бы прекрасными, если бы существовали.

Графы как коды

Чтобы понять, почему так трудно добиться локальной тестируемости, нужно представить сообщение как граф: совокупность вершин (точек), соединённых рёбрами (линиями). Это представление играет центральную роль в понимании кодов с тех пор, как Ричард Уэсли Хэмминг создал первые корректирующие коды. Статья Р. Майкла Таннера 1981 года укрепила позицию графического представления.

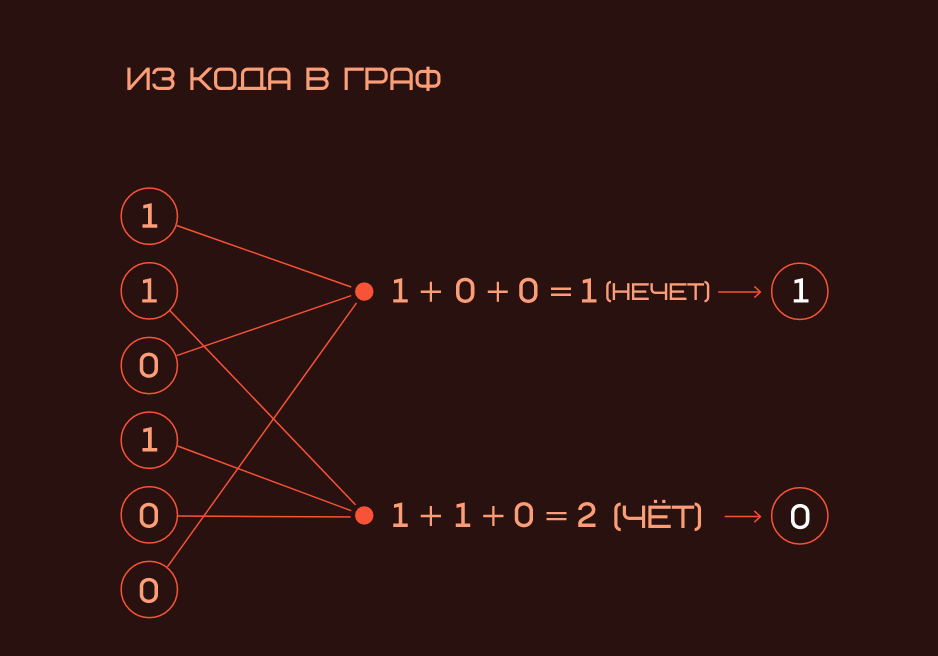
Работа Хэмминга заложила основу для корректирующих кодов с проверкой на чётность. Он придумал правило, согласно которому каждое сообщение делится на пакет данных. Каждый такой пакет сопровождается проверочным битом, в котором учитывается количество битов в сообщении. Каждый проверочный символ в коде Хэмминга представляет сумму по модулю 2 подпоследовательности данных в сообщении. Когда эта сумма имеет чётное значение, проверочный бит 0, а когда она имеет нечётное, проверочный бит отмечается 1.

Хэмминг определил процедуру добавления проверочных битов к сообщению. Получатель может обнаружить ошибки, рассчитывая биты чётности при получении данных. Эти коды работают, они отправная точка для рассмотрения кодов как графов и графов как кодов.

Графы расширяют возможности

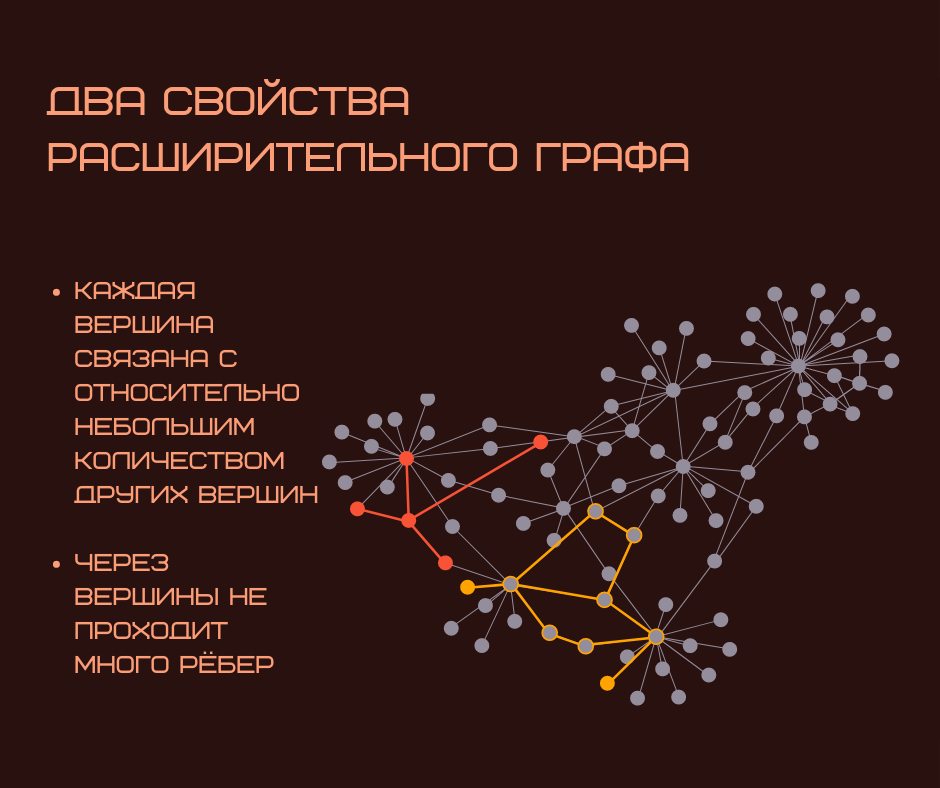
Расширительные графы отличаются двумя свойствами, которые, кажется, противоречат друг другу.

• Во-первых, они разреженные: каждая вершина связана с относительно небольшим количеством других вершин.

• Во-вторых, у них есть свойство расширения — никакой набор вершин не может быть бутылочным горлышком, через которое проходят несколько рёбер.

Другими словами, каждая вершина хорошо связана с другими, несмотря на то, что у графа мало связей.

Майкл Сипсер и Дэниэл Спилмен придумали, как превратить расширительный граф в код. Кодовые слова, которые они придумали, состояли из множества коротких слов на базе кода Хэмминга. Исследователи называли из коротким кодом. Биты кодовых слов были представлены как рёбра расширительного графа. И все контрольные биты коротких кодов были представлены на каждой вершине.

Сипсер и Спилмен показали, что если вы определяете короткие коды в каждой вершине с определёнными свойствами, то, поскольку граф хорошо связан, эти свойства распространяются на глобальный код.

Однако локальное тестирование на этом этапе всё ещё невозможно. Предположим, что существует допустимое кодовое слово из расширительного кода, и вы удалили контрольный бит из одной вершины. Получится новый код с большим количеством допустимых кодовых слов. Для тех, кто работает с исходным кодом, эти новые кодовые слова будут соответствовать контрольным битам на большинстве вершин — кроме той, где контрольный бит стёрли. Но поскольку у обоих кодов большое расстояние Хэмминга, новое кодовое слово, которое кажется правильным, будет чрезвычайно далеко от исходного набора кодовых слов. Локально протестировать расширительный граф нельзя. Исследователи должны были понять, как бороться со случайностью.

Противоположность случайности

Никто не мог сказать, что задачу когда-то получится решить. К 2007 г. учёные добрались до возможности локального тестирования, но только за счёт снижения других параметров, таких как скорость и расстояние. Эти параметры ухудшаются по мере увеличения кодового слова. В мире, где нужно отправлять и хранить крупные сообщения, такой код не нужен. Хотя на практике даже существующие локально тестируемые коды уже были более мощными, чем требовалось большинству инженеров.

Гипотеза о том, что можно создать код с оптимальной скоростью, расстоянием и локальной проверяемостью, которая останется неизменной даже при увеличении сообщений, стала известна как гипотеза c³.

В 2017 году появился новый источник идей. Динур и Любоцки начали работать вместе в Израильском институте перспективных исследований. Они пришли к выводу, что результат математика Говарда Гарленда, полученный в 1973 году, поможет решить задачу.

Обычные расширительные графы — это одномерные структуры, каждое ребро которых простирается только в одном направлении. Гарланд создал математический объект, который можно интерпретировать как расширительный граф, охватывающий более высокие измерения. Например, с рёбрами, переопределёнными как квадраты или кубы.

У графов Гарланда были свойства, которые казались подходящими для локальной тестируемости. Такие графы нужно преднамеренно строить с нуля — то есть они противоположны случайности. Их вершины настолько взаимосвязаны, что их локальные характеристики становятся практически неотличимыми от глобальных.

Любоцки и Динур пытались решить гипотезу c³. Вскоре к команде присоединились Эвра, Ливне и Мозес — эксперты в крупных расширительных графах.

Распространение ошибок

В новой работе авторы выяснили, как собрать расширительные графы для создания нового графа, который приводит к оптимальной форме локально тестируемого кода. Они называют свой граф комплексом Кэли.

Строительными блоками графа являются уже не одномерные рёбра, а двумерные квадраты. Каждый информационный бит кодового слова назначается квадрату, а биты чётности назначаются краям и углам, которые являются вершинами. Каждая вершина определяет значения битов или квадратов, которые могут быть с ней связаны.

Чтобы понять, как выглядит граф, представьте, что вы наблюдаете за ним изнутри, стоя на единственном ребре. К каждому ребру прикреплено фиксированное количество квадратов. Вы как будто смотрите на книгу со стороны её корешка. Однако с других трёх сторон от книги ответвляются новые книжные корешки. Так до бесконечности

Сложный граф разделяет свойства расширительного графа: разреженность и связность, но с другой локальной структурой. Наблюдатель в одной вершине многомерного графа может сделать вывод о связанности всего графа.

При чём тут локальная тестируемость кода? В расширительном графе так: если бит, который является ребром, ошибочен, эту ошибку можно обнаружить только путём проверки контрольных битов в соседних узлах. Но в комплексе Кэли иначе. Если бит (квадрат) ошибочен, эта ошибка видна из нескольких разных вершин, в том числе из тех, которые даже не связаны друг с другом ребром. Таким образом, тест на одной вершине может выявить информацию об ошибках на удалённых вершинах. 

Новый код поддерживает скорость, расстояние и другие свойства, даже в масштабе кодовых слов, что доказывает верность гипотезы c³.

Вскоре должны появиться практические и теоретические приложения: в децентрализованных финансовых системах, например. 

В информатике существуют теоретические конструкции — вероятностно проверяемыми доказательства. Они похожи на коды с локальной тестируемостью. Так что теперь есть повод ждать прорыва в этой области.

Новый код — это прогрессивный шаг, выходящий за рамки случайно сгенерированных шифров. Остаётся только один вопрос: есть ли какие-то реальные пределы качеству подделки информации.