Некто когда-то сказал, что прогресс науки это результат бесконечного спора между учеными, которые регулярно пытаются опровергнуть или перепроверить теории друг друга. Безусловно, в этом есть смысл, ибо теория одного человека, какой бы идеальной она ни была на первый взгляд, остается умозаключением лишь одного человека. Следовательно, в споре рождается истина. Сегодня мы рассмотрим исследование, в котором ученые из университета Арканзаса предложили собирать энергию из Броуновского движения атомов графена. Загвоздка в том, что небезызвестный физик Ричард Фейнман уже давно говорил, что подобное невозможно. Как ученым удалось оспорить это высказывание, что для этого потребовалось, и насколько эффективен разработанный графеновый генератор энергии? Ответы на эти вопросы мы узнаем из доклада ученых. Поехали.
Основа исследования
Отдельно стоящие двумерные (2D) кристаллические мембраны демонстрируют уникальное внеплоскостное движение. В расслабленном состоянии листы отдельно стоящего графена имеют волнистую морфологию, в которой соседние области чередуются между вогнутой и выпуклой кривизной. Происхождение этой ряби нанометрового размера остается неизвестным.
Теоретические исследования утверждают, что источником этого является электрон-фононная связь, поскольку она подавляет жесткость длинноволнового изгиба и усиливает внеплоскостные флуктуации. Для состояния теплового равновесия была выведена система уравнений высоты графеновой мембраны, включая вспомогательные поля напряжений и кривизны. В рамках этой пертурбативной формулировки квантовой статистической механики круглые графеновые мембраны спонтанно изгибаются ниже критической температуры и выше критического радиуса. В этом же русле были проведены и численные исследования статической ряби в мембране, связанной с фермионами Дирака*. Они показали наличие фазового перехода от плоской к волнистой морфологии.
Фермион Дирака* — фермион (частица с полуцелым спином), который не является античастицей.
Однако, как заявляют ученые, ранее не проводилось никаких исследований динамических флуктуаций с использованием гамильтониана*, включающего электроны Дирака, упругость и электрон-фононное взаимодействие.
Гамильтониан* — оператор* полной энергии системы, куда входит и кинетическая, и потенциальная энергии.
Оператор* — линейное отображение, действующее на волновую функцию, которая является комплекснозначной функцией, наиболее полно описывающей состояния системы.
Ранние феноменологические исследования моделировали электрон-фононное взаимодействие путем связывания точечных частиц в узлах гексагональной решетки со спинами Изинга*, которые претерпевают глауберовскую динамику*.
Модель Изинга*: каждая из вершин кристаллической решетки обозначается числом (спином), равным либо +1, либо -1. У спина имеется 2N (N — число атомов решетки) возможных вариантов расположения, каждому из которых приписывается энергия, получаемая из попарного взаимодействия спинов соседних атомов.
Глауберовская динамика* — метод моделирования модели Изинга на компьютере. Является разновидностью алгоритма Монте-Карло с марковскими цепями.
Спины обмениваются энергией с тепловым резервуаром*, их динамика демонстрирует рябь, а их взаимодействие с мембраной приводит всю систему в состояние равновесия.
Тепловой резервуар* — термодинамическая система с достаточно большой теплоемкостью, позволяющей сохранять свою температуру на стабильном уровне даже при контакте с другими системами и/или окружающей средой.
Относительно недавнее исследование (Anomalous Dynamical Behavior of Freestanding Graphene Membranes) позволило измерить движение атомов вне плоскости в отдельно стоящем графене с помощью сканирующей туннельной микроскопии (СТМ). Результаты этих измерений показали, что отдельные атомы в мембране испытывают броуновское движение* со спорадическими (редкими / одиночными) большими скачками.
Броуновское движение* — беспорядочное движение микроскопических видимых взвешенных в жидкости или газе частиц твердого вещества, вызываемое тепловым движением частиц жидкости или газа.
Редкие скачки высоты атомов графена соответствуют когерентным инверсиям кривизны ряби, на которой сидят атомы. Это согласуется как с молекулярной динамикой, так и с глауберовской динамикой спиновых мембран.
Для рассматриваемого нами сегодня исследования графен был выращен на Ni и перенесен на сверхтонкую медную сетку с решеткой из квадратных отверстий (ширина 7.5 мкм) и стержневых опор (ширина 5 мкм). РЭМ (растровая электронная микроскопия) исследование подтвердило, что 90% сетки было успешно покрыто графеном.
В работе использовался сканирующий туннельный микроскоп в условиях сверхвысокого вакуума (базовое давление 10-10 мбар) при комнатной температуре. Графеновая пленка была прикреплена к пластине для образцов на специальных стойках, позволяя наконечнику СТМ проходить через отверстия сетки. Также использовалась система шумоподавления и виброизоляции. Питание системы осуществлялось посредством аккумуляторной батареи с изолированным заземлением для достижения исключительно низкого механического и электрического шума.

Изображение №1
Точка контакта СТМ-иглы (зонда) и образца была включена в электрическую цепь (1а). Образец был изолирован от земли и подключен к двум диодам. Точка контакта в цепи выполняет роль переменного конденсатора. Туннельный ток, ток диода №1 (D1C) и ток диода №2 (D2C) контролировались одновременно. Такая диодная схема используется для сбора энергии, но в данном случае она использовалась, чтобы изолировать индуцированный графеном ток от тока батареи. При расстоянии между зондом и образцом менее 2 нм туннельные электроны преобладают в токе, а в случае больших расстояний преобладает ток смещения.
На 1b показан волнистый графен и изменения формы, вызванные напряжением. Когда напряжение смещения увеличивается, графен растягивается, и СТМ-игла перемещается вместе с графеном. На 1с показано типичное измерение высоты мембраны во времени в точечном режиме с постоянным током. Важно отметить, что в ходе данного эксперимента игла микроскопа передвигалась исключительно вертикально.
График 1d показывает туннельный ток в зависимости от времени как для неподвижного графена (т.е. графена на меди), так и для отдельно стоящего графена. Для отдельно стоящего образца средний ток такой же, как у неподвижного образца, но колебания в 100 раз больше (10 пА против 0.1 пА). Важно и то, что результаты, показанные на 1d, не зависит от приложенного напряжения смещения (до 3 В) и настройки усиления обратной связи.
По мере увеличения уставки* тока (SPC от setpoint current) стандартное отклонение также увеличивается (1e), что может быть связано с нагревом образца.
Уставка* — желаемое или целевое значение важной переменной или процесса в системе.
При экстраполяции к нулевому туннельному току флуктуации по-прежнему вносят вклад в ток смещения в размере 20 пА.
Чтобы измерить ток смещения при нулевом туннельном токе, иглу СТМ постепенно отклоняли от образца, пока расстояние не стало слишком большим для туннелирования электронов через вакуумный барьер. В этом положении SPC находится на уровне 50 нА, тем самым используя цепь обратной связи, чтобы игла СТМ оставалась неподвижной.
После этого было приложено напряжение смещения постоянного тока и отслеживание D2C во времени (2а).

Изображение №2
При одном вольте ток не индуцируется, но при 15 В и 45 В систематически наблюдались резкие и зависящие от времени пики D2C.
На 2b показаны вольт-амперные характеристики (ВАХ) диода при низком значении тока. Далее были проведены расчеты мощности, рассеиваемой в диоде №2 (2c), которая достигает 40 пВт.
На 2d собраны данные по средней мощности для большого количества отдельно стоящих и неподвижных образцов. Отсутствие тока для неподвижного образца подтверждает, что загрязнение и эмиссия электронного поля не являются источниками D2C.
Эти данные предполагают, что электрическая работа* совершается на D2 движением графена, даже если он поддерживается при одной температуре (т.е. при комнатной температуре).
Электрическая работа* — работа, совершаемая над заряженной частицей электрическим полем.
Ученые уверены, что работа может выполняться, находясь в термодинамическом равновесии, и более глубокое понимание этого прольет свет на потенциальные методы получения неравновесной энергии. Для этого была создана модель (3а).
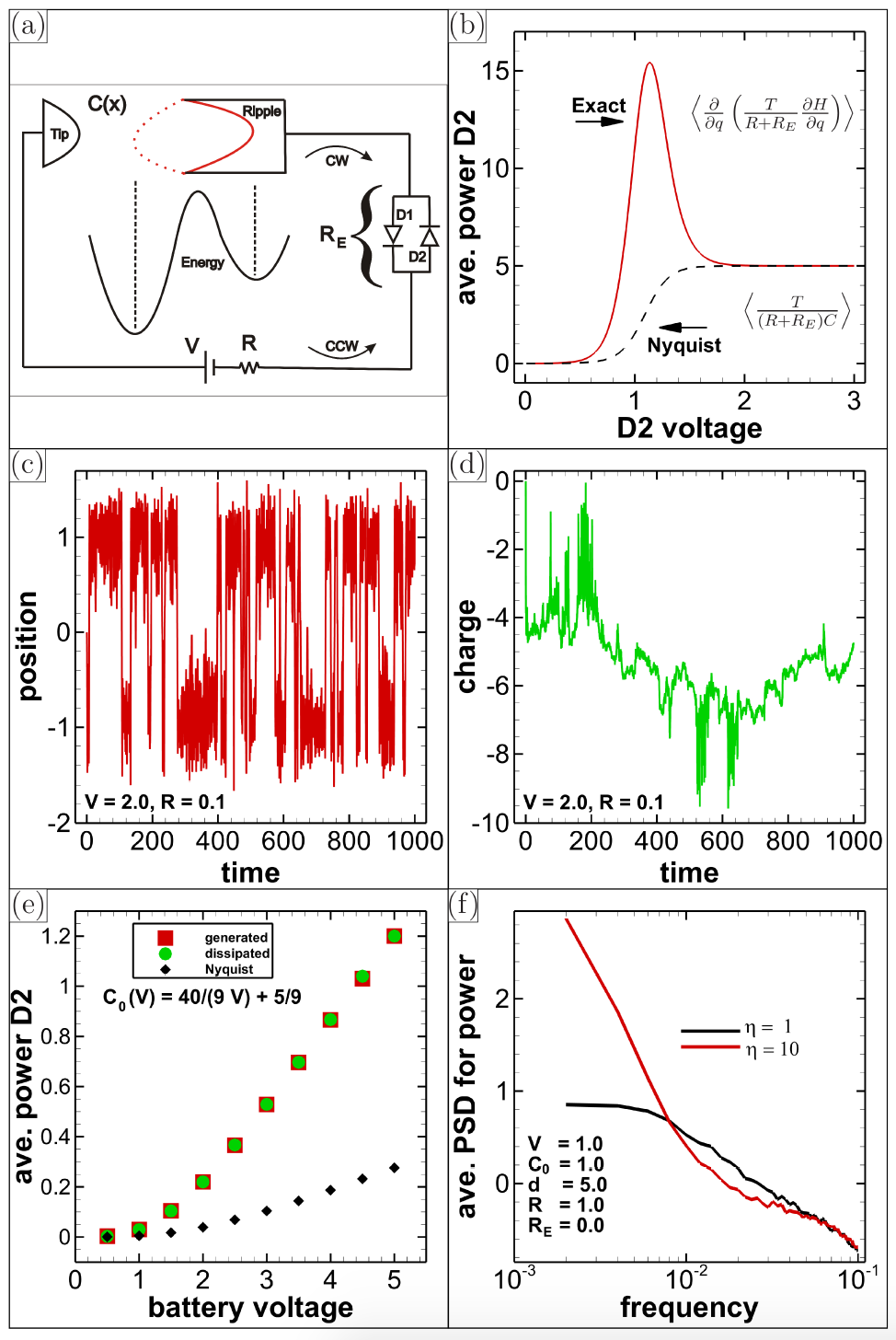
Изображение №3
Атом углерода, ближайший к игле СТМ, находится над волнистостью, которая колеблется между выпуклой и вогнутой кривизной. Данная ситуация моделируется как броуновская частица в двухъямном потенциале, контактирующая с тепловым резервуаром при температуре T.
Игла СТМ и образец действуют как конденсатор переменной емкости C(x) = C0 / (1 + x/d), где d + x(t) — мгновенное расстояние между иглой СТМ и образцом, x(t) (x ≪ d) — вертикальное положение атома углерода, измеренное по отношению к плоской конфигурации графеновой мембраны.
Если мгновенный заряд и падение напряжения конденсатора игла-образец равны q(t) и u(t), то электростатическая сила, действующая на частицу будет равна qu / [2(d + x)] = q2 / (2C0d).
Формула заряда q(t) следует из правил Кирхгофа (соотношение между токами и напряжениями на участках электрической цепи). Следовательно, связанные системы частиц и цепи удовлетворяют уравнениям Ланжевена-Ито (описывает броуновское движение):

где U(x) = x4 — 2x2 это двухъямный потенциал;
C0V2/2d это постоянное напряжение из-за растяжения графена;
R = R + RE это полное сопротивление;
1/RE = 2I0/uD sinh uD/Te это эквивалентное сопротивление диодов;
uD — падение напряжения на диодах, Te = T/e;
∂/∂q·(T/R) это коррекция дрейфа, вызванного шумом;
v и q это независимый и одинаково распределенный белый шум с дельта-корреляциями ⟨ξi(t)ξj(t’)⟩ = δijδ(t — t’) i,j = v, p.
Уравнение цепи имеет шум Найквиста (тепловой шум*) при температуре T, которая установлена на том же уровне, что и пульсация графена.
Тепловой шум* — равновесный шум, вызванный тепловым движением носителей заряда в проводнике, в результате чего на концах проводника возникает флуктуирующая разность потенциалов.
Член ∂/∂q·(T/R) гарантирует детальное равновесие* и факт того, что вся система достигает теплового равновесия при температуре T.
Принцип детального равновесия* заключается в равенстве вероятностей прямого (n → m) и обратного (m → n) переходов между дискретными состояниями системы m и n.
Чтобы убедиться в правдивости данного утверждения, необходимо было сформулировать уравнение для плотности вероятности электронов со скоростями переходов, подчиняющимися детальному равновесию. Вероятность перехода была представлена как T(iD1 + iD2)/(e2uD) = T/(e2R), что согласуется с правилом Кирхгофа для токов.
Гамильтониан системы (3а) был равен:

А равновесная плотность вероятности равна e-H/T/Z, где Z — константа нормализации.
С точки зрения графеновой ряби, представленной частицей в формуле №1 цепь представляет собой внешнюю систему, которая воздействует на рябь. В таком случае тепло, создаваемое силами трения и шума, будет равно:

где q = q(t) — внешний параметр, а d’Q > 0, если частица поглощает тепло.
Используя равновесную плотность вероятности для вычисления среднего и интегрирования по частям, средняя мощность, поглощаемая частицей, оказывается равной нулю. Падение напряжения такое же, как падение на эквивалентном резисторе R. Усредненная по времени мощность, рассеиваемая на резисторе, равна усредненной по времени мощности, поставляемой тепловым резервуаром.
Таким образом, с точки зрения резистора, движение графеновой ряби создает постоянный источник средней тепловой мощности (3b).
Данные выводы были подтверждены посредством численного моделирования уравнения №1, в котором использовались T = 0.5; Ƞ = 1; d = 10; I0 = 0.0002 и Te = 0.1. Чтобы учесть изменение формы графена, было включено падение C0 с 5 до 1 при увеличении V от 1 до 10. Положение частицы x и заряд на конденсаторе q колеблются со временем (3с и 3d).
Отдельно были определены два члена средней мощности для полупериода q̇ > 0, в котором ток через диод №2 проходит против часовой стрелки. Даже в полупериоде два члена равны. На 3е показана средняя мощность (генерируемая и рассеиваемая) и прогноз Найквиста.
Демонстрация принципа работы разработанной цепи.
Было обнаружено, что мощность увеличивается с увеличением напряжения смещения, что наблюдалось и в ходе экспериментов. Данные по сопротивлению и мощности из экспериментов (изображение №2) позволили оценить электрическую емкость точки контакта иглы микроскопа и графена, которая равна 1 фФ (фемтофарад).
Ученые отмечают, что точная формула тепловой мощности отличается от варианта Найквиста: мощность включает в себя вклады от броуновского движения ряби графена, а не только от электронов. В результате двухъямный потенциал вводит новую шкалу времени — скорость пересечения барьера. Это приводит к возникновению колебаний очень низкой частоты. Для иллюстрации этого на 3f показана средняя спектральная плотность мощности, рассеиваемая в резисторе, построенная с использованием двух разных времен релаксации скорости 1 и 10. Общая рассеиваемая мощность такая же, а уменьшение скорости пересечения барьера перераспределяет мощность на более низкие частоты.
Для более детального рассмотрения результатов исследования рекомендую заглянуть в доклад ученых.
Эпилог
В данном труде ученые провели исследование термического воздействия в отдельно стоящих графеновых мембранах с помощью точечной сканирующей туннельной микроскопии. Пульсация графена, наблюдаемая рядом с иглой микроскопа, была смоделирована как броуновская частица в двухъямном потенциале. Когда графен движется, заряд должен проходить по цепи и выполнять электрические работы.
Данная модель показывает, что непрерывная тепловая энергия может генерироваться броуновской частицей при одной температуре, находясь в термодинамическом равновесии, при условии, что такое же количество энергии постоянно рассеивается в резисторе. В таком случае подключение к цепи позволяет выполнять электрические работы на нагрузочном резисторе без нарушения второго закона термодинамики.
В условиях созданной системы графен и электрическая цепь поддерживают работу друг друга. Несмотря на то, что тепловая среда выполняет работу с нагрузочным резистором, температура графена и цепи остается одинаковой, а тепло между ними не протекает. Таким образом нет противоречий по отношению к второму закону термодинамики.
Важно и то, что относительно медленное движение графена индуцирует ток в цепи на низких частотах. Эта находка может стать очень полезной в будущем, поскольку электроника работает более эффективно именно на низких частотах.
В будущем ученые намерены продолжить свое исследование. Они хотят выяснить, можно ли хранить постоянный ток в конденсаторе для последующего использования. Для реализации этой задумки необходимо провести миниатюризацию схемы и нанесение ее на кремниевую пластину или микросхему. По словам ученых, если успешно построить кластер из миллиона таких схем размером 1х1 мм, то он смог бы заменить маломощные батарейки.
Возможно, подобные планы звучат не особо грандиозно, но любые исследования, любые свершения, изменившие мир, начинались с малого. Для достижения конечного результата нужно лишь упорство, время и терпение.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. 🙂
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?

