[Из песочницы] Ticket to Ride.Европа — скромные шаги в арифметику игры

День первый. Нам подарили игру «Ticket to ride. Европа». Это моё первое знакомство с игрой данной серии, надо обязательно попробовать и заценить.

День пятый. Как-то надоело регулярно проигрывать, пора бы призвать на помощь математику и попробовать таким образом одержать заслуженную победу.

С помощью гугла, excel и python и чёртовой матери была проведена познавательная экскурсия в механики игры. Волшебной таблетки не нашлось, но что-то полезное на выходе получилось.

Очки в игре можно набрать четырьмя различными способами. Предлагаемая теория хорошо подходит для одного из них под названием «построить большое количество маршрутов».

Аксиомы игры

1. Всего на поле расположено 46 городов. Между городами проходит 90 маршрутов безотносительно типа (паромная переправа, туннель, двойной). Максимально на поле помещаются 300 вагонов (с использованием обоих перегонов на «двойных» участках) — в среднем, длина перегона равна 3.33 вагона
2. На игровом поле встречаются следующие перегоны:
   

   	Обычный перегон	Двойной перегон	Туннель	Двойной туннель	Паромная переправа	Двойная паромная переправа
   Цветной	Есть	Есть	Есть	Есть
   Серый	Есть		Есть		Есть	Есть

   Ни один перегон не может быть одновременно паромом и туннелем.

Откровение первое: не все вагоны одинаково полезны

Если внимательно посчитать все цветные перегоны между городами, получится, что максимальная потребность в вагончиках примерно одинаково. Однако, если включить «поправочный коэффициент» для участков, отличных от обычного перегона, ситуация существенно изменится (разница между самыми востребованными и менее нужными цветами достигает почти 20%).

• Потребность в вагонах для обычного перегона оценивается как 100% длины перегона (считаем, что для перегона используются только цветные вагоны).
• Потребность в вагонах для двойного перегона оценивается как 50% (считаем, что для перегона могут быть использованы вагоны любого из двух цветов. Например, для строительства участка Париж-Франкфурт могут быть использованы как белые, так и оранжевые вагоны).
• Был затрачен литр кофе, чтобы на основе теории вероятности рассчитать потребность в вагонах для строительства туннеля, в конечном итоге она была высчитана методом Монте-Карло. Эмулировано извлечение трёх карт из полной колоды, зафиксирована вероятность выпадения «игровых карт» — локомотивов, либо вагонов того же цвета. (Здесь и далее: каждый раз считалась вероятность для полной колоды, не учитывались карты, которые уже могут быть на руках у юзеров).
  

  Доп. вагоны	Вероятность
  0	44,14%
  1	41,95%
  2	12,71%
  3	1,2%

  Итоговая «средняя по больнице» потребность в вагонах для строительства туннеля длиной N составляет:

  $\$\$display\$\$=N+1*0.4194+2*0.1271+3*0.012=N+0.709\$\$display\$\$$

• Двойной туннель считается как смесь правил 2 и 3

Прогнав все 90 путей через программу, написанную по этим простым правилам, получаем на выходе (указано общее количество участков нужного цвета и «реальная» потребность в вагонах):

Серые вагоны в природе отсутствуют — при строительстве перегона заменяются нужным количеством любого цвета. Путаница с разделителями целой и дробной части возникает из-за использования двух инструментов – Excel и Python, каждый из которых обозначает вещественные числа по-своему. Можно было бы поковыряться в настройках отображения, но зачем? На результатах это никак не сказывается

Отсюда рождается первый совет: В общем случае для строительства «серых» маршрутов выгоднее использовать чёрные или белые вагоны. Зелёные и голубые по возможности следует придержать и использовать по назначению.

Откровение второе: для строительства перегонов различного типа нужно различное количество ходов

И снова старый-добрый Монте-Карло, который считает сколько нужно раз взять две карты «вслепую» (читай: потратить ходов), чтобы получить нужное количество вагонов и/или локомотивов для строительства перегона нужной длины и нужного типа. Для строительства перегона нужен ещё один ход, на выходе получается такая таблица:

которая мало что даёт сама по себе, но служит основой для будущих расчётов.

Двойной цветной туннель «Памплона-Мадрид» (длиной 3 вагона) в таблицу не вошёл, для него количество ходов посчитано отдельно, оно составляет 7,511.

Откровение третье: не все города одинаково важны

В левом верхнем углу карты расположен город Эдинбург, к нему подходит один двойной путь из Лондона. При этом, Эдинбург является конечной станцией для двух маршрутов (Эдинбург-Афины (21) и Эдинбург-Париж (7)). То есть, при игре вдвоём-втроём есть вероятность, что за перегон Лондон-Эдинбург развернётся война и один из игроков останется с незавершённым маршрутом.

Ещё для 4 городов количество подходящих путей совпадает с количеством маршрутов, начинающихся или оканчивающихся в данном городе.

Город	Путей	Конечная
Эдинбург	1	2
Копенгаген	2	2
Стокгольм	2	2
Брест	3	3
Смоленск	3	3

Совет второй: Если ваши маршруты начинаются или оканчиваются в указанных городах, стройте пути в нужном направлении при первой же возможности.

Если ограничиваться не только конечными станциями, но и промежуточными (о методе «вычисления» промежуточных станций см. в пятом откровении), получается своеобразный рейтинг «загруженных» городов, которые нужно «опоясывать» в первую очередь.

Город	Путей	Конечная	Промежуточная
Париж	7	3	11
Берлин	5	4	8
Франкфурт	6	2	9
Вильно	5	2	6

На другом краю рейтинга расположились города, малоинтересные с точки зрения маршрутов – их можно оставить на потом, на самый конец игры (главное, чтобы вагонов хватило).

Город	Путей	Конечная	Промежуточная
Севастополь	5	1	1
Петроград	4	2	0
Рига	3	1	0
Ангора	3	2	0
Афины	4	3	0
Барселона	3	2	0
Брюссель	4	2	1

Откровение четвёртое: не все маршруты одинаково полезны

К текущему моменту имеются следующие данные:

• Перечень маршрутов с карточек.
• Список перегонов между городами.
• Усреднённое количество ходов, которые нужно потратить, чтобы построить перегон того или иного типа.

Вполне возможно найти для каждого маршрута самый быстрый путь (путь, которым можно построить маршрут за наименьшее количество ходов). Для этого вполне подходит алгоритм Дейкстры, в качестве весов для перегонов применяется количество ходов, необходимых для постройки оного.

В таблице ниже приведены наиболее и наименее выгодные маршруты, «выгода» от маршрутов (количество полученных очков / количество потраченных ходов) варьируется достаточно ощутимо, при этом «длинные маршруты» (выделены голубым) идут уверенным пелетоном в верхней части таблицы:

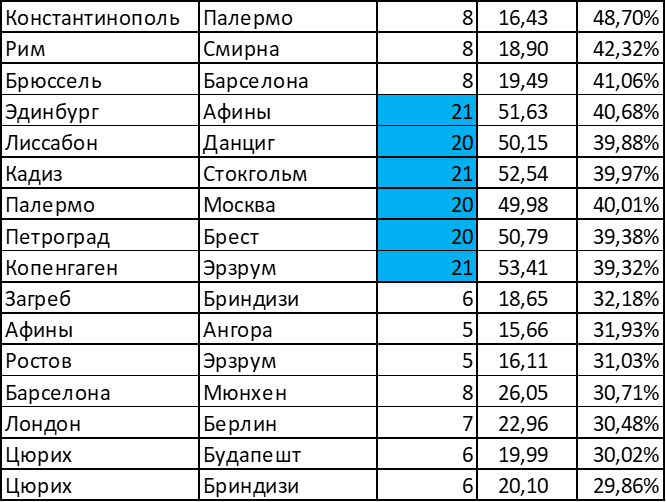
Откровение пятое: не все перегоны одинаково полезны

Когда готов список самых оптимальных путей, можно оценить «загруженность» каждого из перегонов и выбрать «ключевые» участки, которые используются в наибольшем количестве маршрутов.

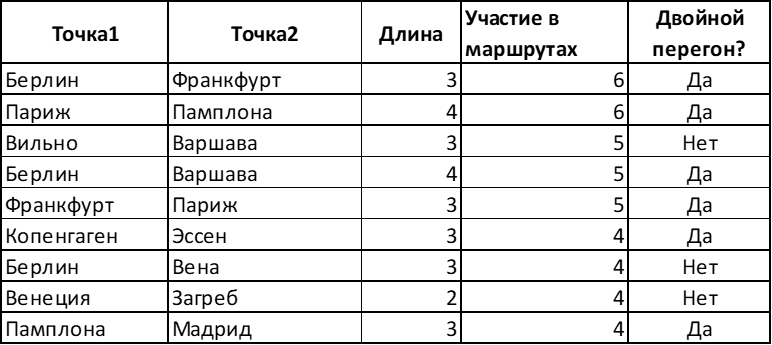
Из-за явной востребованности данных участков, рано или поздно за них возникнет борьба. И будет лучше, если проблемы с занятостью участков возникнут рано и для ваших соперников.

Совет третий: В случае, если ваш маршрут проходит через перегоны, указанные выше (и через перегон Эдинбург-Лондон), занимайте их в первую очередь, по мере наличия вагонов нужного цвета.

В случае, если играют 4-5 игроков, ситуация несколько упростится для двойных перегонов.

На другом конце таблицы имеются перегоны, которые минимально востребованы в среднестатистической игре.

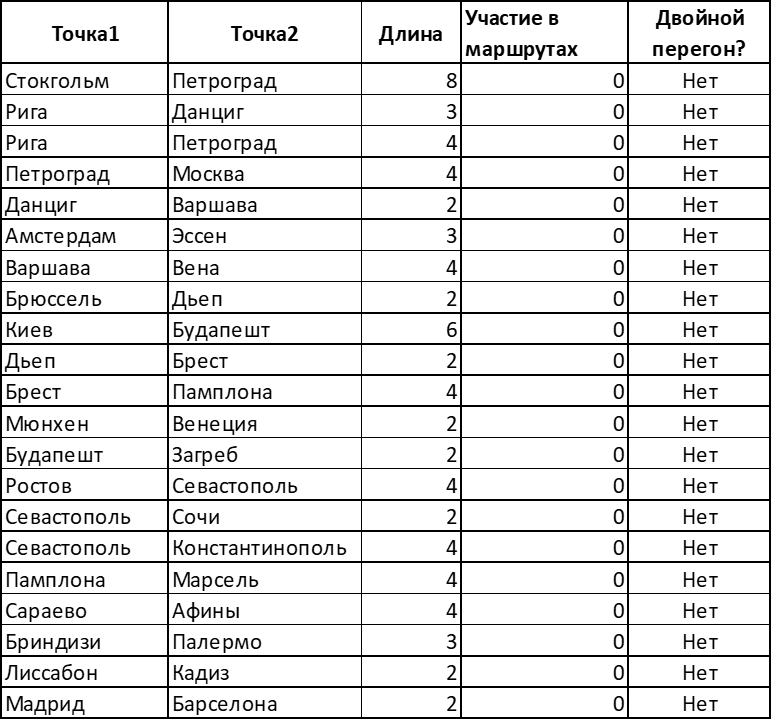
Вообще, если с высоты птичьего полёта взглянуть на тепловую карту загруженности городов и перегонов (чем коричневее, тем загруженнее; белый цвет – нулевая загруженность), станет понятно где скорее всего развернётся борьба.

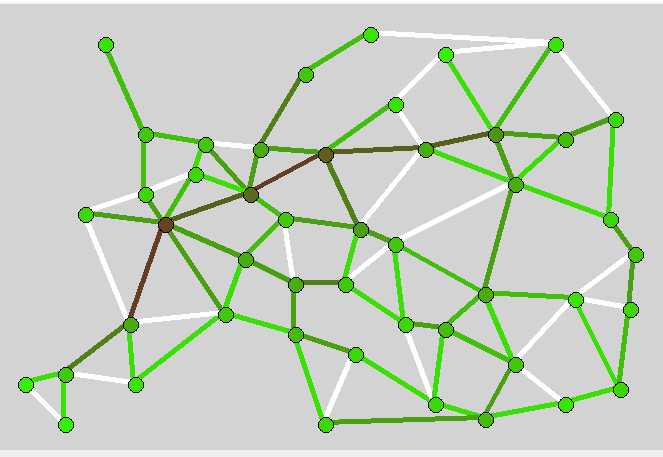
Указанные советы могут быть полезны при игре rush-ем – быстрее всех построить много маршрутов. Математизация наиболее выгодных маршрутов между городами (очки/количество ходов), добавление алгоритмов «самой длинной непрерывной ветки», использование ранее построенных участков и использование путей соперников при помощи станций ещё ждут своих исследователей.

Побед вам и интересных баталий.