Суть разработки такая. Рассмотрим обычный, скажем, 5-ти осевой манипулятор (кинематическая структурная схема изображена на рисунке ниже). Его возможности при перемещении в пространстве широки: он способен совершать движения в 5-ти координатах, причём одновременно, т.е. 3 координаты по трём осям XYZ и вращение вокруг двух из них. В таком случае рабочий элемент манипулятора способен занять любое положение в рабочем пространстве и вместе с этим сохранить требуемую ориентацию рабочего органа (не считая поворот рабочего элемента вокруг собственной оси).
![[Из песочницы] «Ручной» манипулятор [Из песочницы] «Ручной» манипулятор](https://habrastorage.org/webt/h5/gw/vy/h5gwvyur-unszdlq6w-knkvihwe.jpeg)
Данная конструкция относится к манипуляторам антропоморфного типа и поэтому способна, приближённо конечно, воспроизводить движение человеческой руки. Рассуждая над этим тезисом как раз пришла мысль, что интересно бы сделать так, чтобы манипулятор дистанционно мог копировать движения моей руки в реальном времени. Чтобы я просто одевал на руку сенсор, считывающий перемещения руки (как линейные, так и угловые), и эта механическая штука будет повторять их вслед за мной. Как манипулятор может выполнять функции перемещения и ориентирования рабочего органа, так и с помощью руки человек может перемещать и ориентировать свою ладонь, следовательно эти два процесса схожи и их можно представить как один общий процесс — захват движения руки манипулятором в реальном времени.
На этом формулировка задачи завершена. Теперь проведём анализ задания (не поворачивается язык назвать это «техническим заданием»). Необходимо разработать два, конструктивно независимых устройства: непосредственно сам манипулятор и устройство отслеживания движения, которое крепиться на руку. Затем последует трудоёмкий процесс создания математических описаний, составления алгоритма и написания программного обеспечения. Делим проект на три части:
1. Разработка манипулятора
2. Разработка устройства для отслеживания перемещения руки
3. Всё остальное
Вкратце о каждом из этапов:
- Здесь всё тривиально… В САПР проектируем конструкцию, выполняем чертежи деталей и изготавливаем, после собираем. Затем рассчитываем кинематику и пишем собственное программное обеспечение, которое скроет низкоуровневые обращения к приводам.
- На этом этапе определяемся с типом сенсоров, проектируем принципиальную схему, изготавливаем печатную плату, разрабатываем алгоритм определения положения в пространстве, пишем ПО.
- Собственно, ради чего были предыдущие этапы – заставить манипулятор слушаться хозяина. Здесь разрабатываю алгоритм конвертации координат в рабочее поле манипулятора.
1. Разработка манипулятора
В этом проекте, как было сказано выше, используем манипулятор с 5-ю степенями свободы. Такое количество степеней свободы достаточно, т.к. в их число входит три линейных перемещения и два вращательных. Последние два необходимы для ориентации рабочего органа, поскольку направление РО в пространстве можно задавать в виде вектора, а вектор определённо можно восстановить из двух углов поворота (не учитывая длины). В таком случае нам необходимо пять обобщённых координат, равное числу осей.
Звенья манипулятора связаны вращательными кинематическими парами пятого класса. Конструкция манипулятора стандартная для своего типа (кинематическая схема представлена в начале статьи). Имеет в составе неподвижную станину, с которой связана базовая система координат, поворотную стойку, к которой крепятся остальные подвижные звенья, соединённый в цепь. К конечному звену (фланцу) крепиться рабочий орган, в данном случае его имитация в виде стрелообразного указателя (см. изображение ниже).


















ЗD–модель построена в САПР «Компас 3D». Материал деталей – фанера 4 мм и PLA для пластиковых деталей. Детали из фанеры вырезались на лазерном станке, детали из пластика печатались на 3d-принтере. В качестве приводов осей используются цифровые сервоприводы Dynamixel AX-12. Внешний вид манипулятора напоминает одного гнусного насекомого, от которого он получил прозвище «Комар».
Математическое описание кинематики
На этом этапе необходимо рассчитать прямую и обратную кинематику манипулятора. Прямая задача состоит в том, чтобы по известным значениям обобщённых координат (в данном случае углы поворота звеньев) определить положения звеньев относительно некоторой базовой системы координат. Обратная ей задача называется обратной или инверсной кинематикой, заключается в определении параметров обобщённых координат для достижения желаемой позиции и ориентации рабочего органа манипулятора.
Начнём с расчёта обратной кинематики. Изобразим геометрическую схему манипулятора, из которой будут ясны интересующие нас геометрические соотношения.

Требуемую позицию изображаем радиус-вектором . Здесь стоит пояснить, почему вектор проведён до фланцевой точки, а не до конечной точки РО. Поскольку ориентация рабочего органа нам известна заранее (я её сам определяю согласно некоторым требованиям), то необходимо, чтобы фланцевая точка оказалась в нужном месте, указанное как вектор . Этот вектор получается вычитанием из радиус-вектора , проведённого к конечное точки РО, вектора его ориентации , относительно БСК, т.е:
Рассмотрим переход фланцевой точки в нужное положение. Оно осуществляется поворотам звеньев a и b (их я изобразил в виде векторов) в шарнирах A, B и C. Начало базовой системы координат (БСК) поместим в точку шарнира B. Ось вращения шарнира A направлена вдоль оси Z, оси B и C направлены перпендикулярно Z.
Когда всё формальности соблюдены, перейдём к сути. Для решения обратной задачи кинематики я использовал геометрический подход в силу простоты конструкции манипулятора. Из геометрии видно, что вектор равен сумме векторов звеньев и . Углы , , — углы поворота звеньев А, В и С соответственно.
Рассмотрим треугольник, ограниченный векторами , и . Из этого треугольника по теореме косинусов найдём углы и . Пусть длины векторов будут равны:
Запишем теорему косинусов относительно искомых углов:
Выразим углы и :
Из геометрической схемы видно, что:
Тогда:
Окончательно, переход от линейной координаты к углам поворота звеньев осуществляется формулами:
Теперь, когда переместили фланцевую точку в требуемое положение надо правильно сориентировать рабочий орган. Чтобы это сделать, необходимо знать координаты вектора относительно фланцевой точки, т.е. координаты в базисе локальной системы координат (ЛСК) – , начало которой расположено в фланцевой точке манипулятора.
Вектор направлен по звену b, вектор – вдоль оси шарнирного соединения f1.
Для нахождения базиса определим матрицу перехода от БСК (с базисом ) и ЛСК. Эта матрица получается путём комбинации поворотов в шарнирах A, B и C:
где
Т.к. матрица является единичной, тогда:
Матрица вычисляется путём перемножения матриц поворота вокруг оси на угол.
Зададим функцию, которая вычисляет эту матрицу:
Ось берётся в виде вектора как столбец матрицы, полученной предыдущими поворотам, а углы уже рассчитаны выше.
В итоге получаем:
Пусть вектор рабочего органа в БСК . Тогда справедливо равенство:
Отсюда выразим – вектор рабочего органа в базисе , т.е. относительно фланцевой точки:
Теперь, зная вектор РО, можно рассчитать углы поворота ориентирующих осей f1 и f2

Чтобы переместить РО в заданную позицию, требуется совершить поворот на углы и . Из рисунка видно, что
где — длина рабочего органа,
— координаты вектора .
Программное обеспечение манипулятора разделено на два уровня, верхний и нижний. Верхний уровень написан в Matlab в виде библиотеки и различными командами-методами, нижний – на микроконтроллере Atmega328. Задача верхнего уровня состоит в том, чтобы сформулировать команды, отсылаемые на микроконтроллер. Его задача получить команду и в соответствии с ней установить приводы в нужное положение. В таком виде система управления оказалось надёжной (пока что…) и удобной в использовании.
Формулировка команды и отправка со стороны верхнего уровня происходит следующим образом: пользователь в командном окне Matlab вызывает функцию из библиотеки (например, функцию простого перемещения в точку), указывает необходимые аргументы (обычно это координаты и ориентация РО). После по изложенным выше математическим соображения, записанных в библиотеку, вычисляются углы поворота осей и при необходимости скорости вращения. После по простенькому протоколу собираем команду и шлём её на микроконтроллер нижнего уровня по последовательному COM – порту.
Пару слов о написанной библиотеке. В её распоряжении есть следующие функции:
- функции создания соединения по последовательному интерфейсу
- функции перемещения
- в точку, с постоянной скоростью всех приводов
- в точку, с конечным остановом всех приводов (скорость привода подбирается в пропорции от собственного и самого большого угла поворота. Таким образом в конце подхода к точке заканчивают движение все приводы)
- в точку, с плавным перемещение каждого привода (в этом случае график скорости выглядит как трапеция с участками разгона, постоянной скорости и торможения)
График
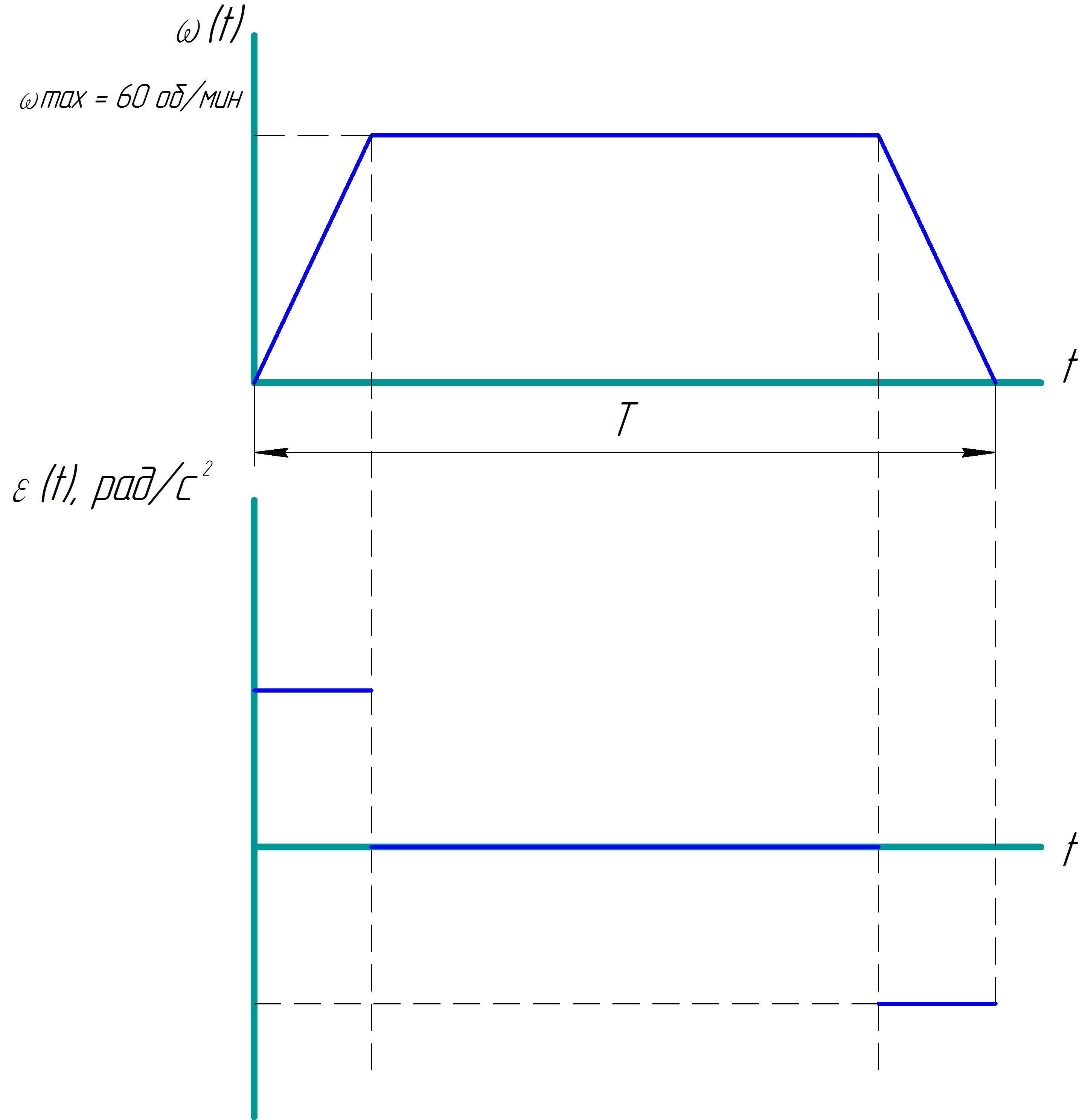
- в точку, по вручную заданным углам поворота осей и скорости вращения
Список функций можно конечно расширить, но достаточно было и этого функционала для решения непосредственно той задачи, для которой манипулятор и проектировался.
На видео продемонстрирована работа манипулятора.
2. Разработка устройства для отслеживания перемещения руки
Переходим к следующему этапу. Здесь потребуется спроектировать специальное устройство, которое может отслеживать в реальном времени положение в пространстве ладони. Также этот процесс носит название «захват движения». Для осуществления задуманного я решил использовать бесплатформенную инерциальную навигационную систему (БИНС) на основе трёх датчиков: гироскопа, акселлерометра и магнитометра. Связка этих датчиков называется IMU – сенсор (в переводе и есть то самое БИНС).
Сперва я спроектировал печатную плату с необходимым мне функционалом, на которой я разместил эти три датчика. В качестве обрабатывающего контроллера я выбрал (точнее взял что было) микроконтроллер Atmega2560. Сенсоры использовал распространённые и дешёвые на китайском рынке. Это спаренные датчики трёхосные гироскоп и акселерометр MPU6050 и магнитометр HMC5883l.
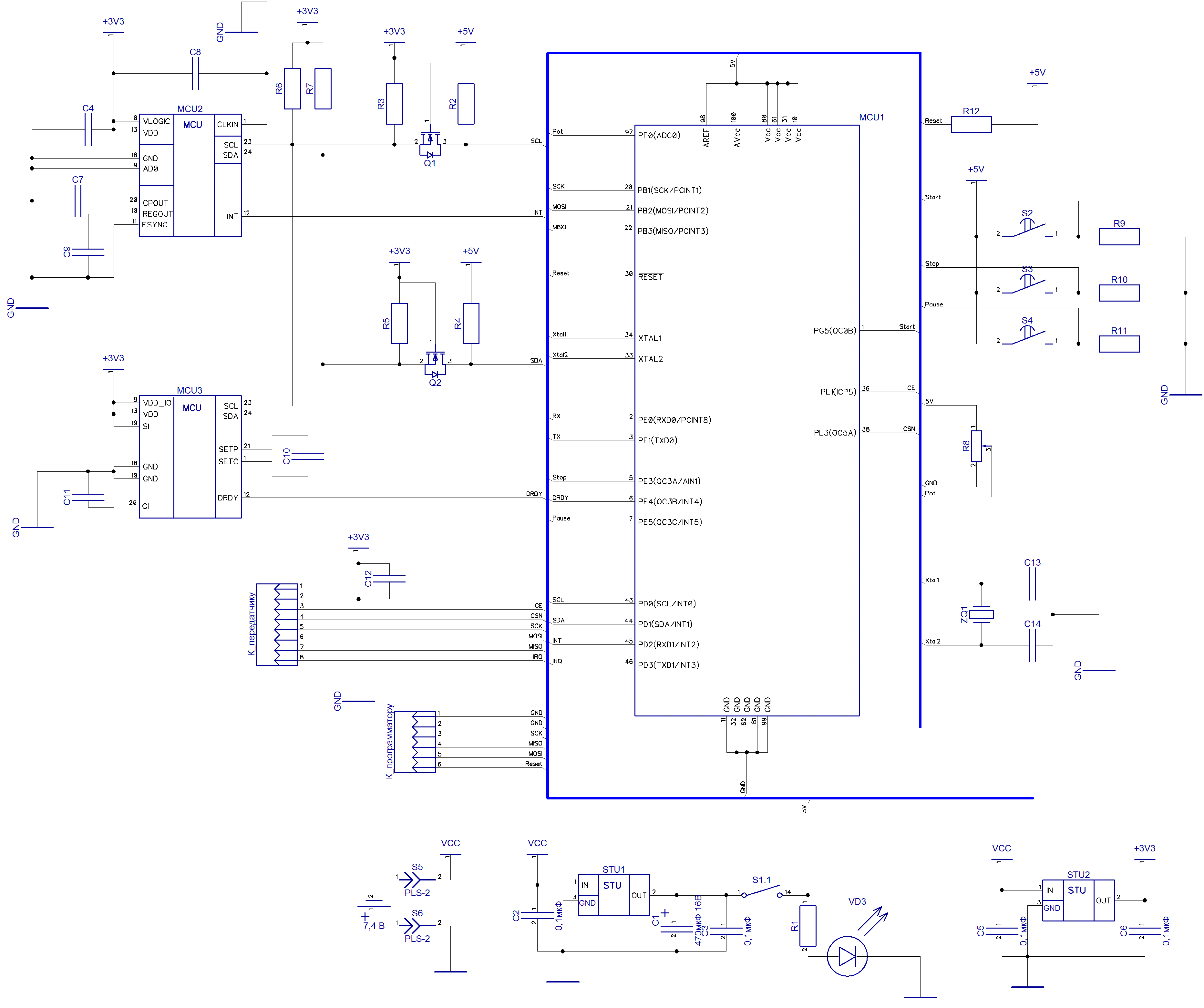


Алгоритм расчёта положения в пространстве достаточно прост: вначале определяем ориентацию в виде базиса локальной системы координат (ЛСК), которая связана с датчиками, а в конечном итоге с ладонью руки.

Ориентацию определяем относительно начальной системы координат (НСК), что по сути является начальным положением устройства в момент включения питания. Базисы НСК и ЛСК состоят вектор-столбцов её орт:
Они связаны соотношением:
Где – матрица перехода, она же матрица вращения в пространстве. Базис НСК будем считать единичной матрицей. Следовательно
.
После, вектор ускорения , который известен относительно ЛСК, необходимо определить в НСК. Это делается путём умножения вектора-столбца ускорения на базис ЛСК:
Затем полученный вектор ускорения два раза интегрируем по времени и получаем расстояние, т.е. координаты:
Первые попытки реализации этого алгоритма были весьма наивны… Наивность была в том, что я посчитал возможным только по данным гироскопа, используя дискретное интегрирование, получить матрицу поворота вокруг оси. Осью в данном случае можно рассматривать как псевдовектор угловой скорости, компоненты которого (проекции на оси) и есть выходные данные с датчика гироскопа. А угол в свою очередь получается интегрированием модуля вектора. Первоначальный задор и энтузиазм пропал, когда я увидел чудовищный по величине, так называемый «дрейф нуля», вызванный накапливающейся ошибкой из-за погрешности дискретного интегрирования и собственного шума датчика. Ещё тогда у меня появились мысли, что по данным акселерометра, который в состоянии покоя показывает вектор, обратный вектору ускорения свободного падения (далее в тексте вектор гравитации), можно делать корректировку матрицы, но и здесь появляется неопределённость, связанная с тем, что корректировка возможно только с точностью до поворота угла вокруг оси Z. Корректировка будет полноценна в том случае, если будет возможным восстановить матрицу поворота альтернативным способом, т.е. без применения данных гироскопа.
Тогда необходимо использовать ещё один фактор, по которому возможно будет сделать полноценную корректировку положения. Этим фактором является магнитное поле Земли, которое наряду с гравитацией в отдельной взятой точке планеты не меняются со временем (в краткосрочной перспективе конечно). Его измеряем при помощи вышеупомянутого датчика HMC5883l. В таком случае мы имеем два вектора, которых достаточно, чтобы относительно них определить положение в пространстве.
Теперь возникает закономерный вопрос – «как это сделать?». После неудачных попыток ответить на это вопрошание самостоятельно я полез в интернет, где нашёл нужную мне информацию. Задача определения ориентации в пространстве по данным трёх измерений (угловая скорость, вектор гравитации и вектор магнитного поля) встаёт также при проектировании любительских летательных аппаратов (например коптеры), поэтому эта задача не раз решалась различными методами. Один из популярных методов – это так называемый фильтр Маджвика (Sebastian O.H. Madgwick). Прочитав оригинальную статью и не поняв англицкого, я обратился к замечательному переводу (спасибо автору за проделанный труд). Пока углублялся в изучении статьи у меня всё чаще и чаще возникала мысль о том, чтобы всё-таки попробовать написать свой алгоритм фильтра определения положения, учитывая, что к этому моменту мой уровень познаний в этой области заметно повысился. Хотя бы ради интереса «изобрести велосипед»! И я его «изобрёл». Ниже привожу свои рассуждения.
В алгоритме используются показания все трёх датчиков. Напомню, задача алгоритма – вычисление ориентации объекта и компенсация дрейфа нуля гироскопа, учитывая данный пары акселерометра и магнитометра. В качестве математического инструмента, описывающего положение, используется кватернион, т.к. он удобен в плане построения и оптимизация алгоритма и требует меньше математических операций для его расчёта в отличие от матриц. Кватернион вращения в пространстве выглядит следующим образом:
Зная ось вращения, описанное нормированным вектором , и угол (откуда они берутся сказано выше) можно рассчитать кватернион:
Тогда, используя только показания гироскопа, на каждой итерации цикла будем рассчитывать текущее значение кватерниона по выражению:
Здесь – кватернион в данный момент времени. Индекс G сверху говорит о том, что это значение относится к измеренному относительно показаний гироскопа, т.е. угловой скорости; – значение кватерниона в предыдущий момент времени; –изменение положение за один шаг измерений, можно сказать дискретное изменение положения на угол за – период дискретизации, выраженное кватернионом вращения (*).
Следующий этап вычислений – нахождение матрицы поворота исходя из данных пары датчиков акселерометра и магнитометра. Конкретно, рассматриваем вектор гравитации и вектор индукции магнитного поля Земли, которые, как это было сказано выше, статичны относительно Земли и связанной с ней НСК. Здесь тезис такой: зная значения гравитации и индукции в базисе ЛСК и НСК можно рассчитать матрицу перехода (поворота) от НСК к ЛСК и кватернион вращения в пространстве.
Обозначим через нормированный начальный вектор гравитации. Его можно принять таким:
Через обозначаем нормированный начальный вектор магнитной индукции:
Также требуется третий вектор , который связан с этими двумя. Он получается векторным умножением на :
Теперь формируется матрица , которая характеризует начальной положение, т.е. НСК, поскольку в начальный момент времени ЛСК совпадает с НСК. Матрица получается из компонентов векторов , и :
Аналогично, но уже на каждой итерации цикла, создаётся подобная матрица , где – текущий нормированный вектор магнитной индукции, – текущий нормированный вектор гравитации, . Эта матрица характеризует положение ЛСК, т.к. эти вектора известны в системе координат датчиков, которая совпадает с ЛСК. Тогда, зная обе матрицы, можно записать такое уравнение:
Оно связывает две матрицы, найденные при разных обстоятельствах. Учитывая выражение и то, что базис – единичная матрица, получим:
Отсюда выразим матрицу перехода :
Первый множитель, как можно понять, рассчитывается только один раз в самом начале алгоритма, и не требует пересчёта в процессе работы. Второй множитель формируется довольно таки легко и не принуждённо на каждой итерации цикла.
После, когда найдена матрица перехода, преобразуем её в кватернион (алгоритм конвертации из матрицы в кватернион вещь публичная и приводить здесь его не буду).
В итоге нам известны два кватерниона, найденные независимо друг от друга. И для совмещения результатов я применил простенький комплементарный фильтр с коэффициентом , который берётся из диапазона от 0 до 1:
В результате получаем кватернион, в котором находится актуальная информация о положении в пространстве устройства с модулем БИНС.
«Велосипед» поехал… Алгоритм работал, но в некоторых положениях вёл себя несколько не адекватно, что в принципе не мешало, но и не давало повода думать о нём положительно. Свой спортивный интерес я удовлетворил, и теперь можно обратиться к готовым решениям, более качественным. Тогда я вновь вернулся к статье Себастьяна Маджвика и решил использовать его алгоритм, благо, что этот замечательный человек опубликовал все исходники на сайте проекта. В архиве были исходный коды на разных языках, в том числе и на языке Matlab. Этот факт повлиял на моё решение отказать от идеи делать все вычисления на микроконтроллере (тем паче что он 8-ми битный) и писать программу уже на компьютере в среде Matlab. Микроконтроллер используется только для опрашивания датчиков и отсылку данных на ПК (похожая ситуация и с манипулятором). В таком случае основной программный код, который подвергается изменениям и отладке, базируется в среде Matlab, что весьма удобно в процессе работы.
Хорошо, ориентацию, заданную кватернионом, мы получили. Что дальше по плану? А далее следует нахождение линейных координат объекта по данным акселерометра. Что ж, здесь лучше просто констатировать, что невозможно с нужной точностью по акселерометру определить координаты. Даже хотя бы находить изменение положения, которое было бы адекватным! Конечно, были попытки решить эту задачу, но в режиме реального времени находить координаты не получалось. Почему? Потому, что двойное дискретное интегрирование зашумленных показаний датчика приводила только к полёту в стратосферу, причём с бешеной скоростью, но никак не к положительному результату. Поэтому обозначенный в начале пункта алгоритм я обрезал до момента нахождения ориентации, и на этом остановился.
3. Всё остальное
Итак, вот я подобрался к заключительному этапу проектирования, вдоволь наигравшись с манипулятором и навертевшись IMU-сенсором. Работая над двумя предыдущими этапами я уже чётко представлял, как всё будет работать и по какому алгоритму. Поэтому с этим этапом я расправился достаточно быстро. Поскольку известна только ориентация ладони, то работаем непосредственно с рабочим органом, который требуется соответственно ориентировать. РО может принять любое направление, если оно не нарушает рабочую зону (вращаться на все 360 не получиться).
В пункте про разработку манипулятора вектор РО задавался вручную, и уже после находились углы поворота приводов. Так вот, этот вектор и нужно определить исходя из ориентации ладони руки. Ориентацию можно выразить базисом , найдя его, конвертировав кватернион в матрицу. Базис состоит из вектор-столбцов его орт, следовательно получаем три вектора , и . Будет удобным взять за ориентацию РО вектор , поскольку я предполагал такое начальное положение манипулятора, когда все звенья и РО расположены в плоскости XZ базовой системы координат, и РО в этот момент расположен горизонтально, т.е. вектор в начале сонаправлен с осью X БСК и НСК (начальное положение модуля БИНС располагаем так, чтобы НСК совпадала БСК манипулятора). В таком случае первый столбец матрицы приравниваем вектору . После нормируем его по длине РО и получаем требуемый вектор относительно базовой системы координат манипулятора. Затем следуем последовательности расчёта обобщённых координат из п. 1.
Стоит заметить, что манипулятор, при изменении ориентации РО, способен выполнить перемещение в двух режимах: первый – когда фланцевая точка неподвижна, второй – когда неподвижна конечная точка РО, но соблюдается его ориентация. Второй режим вызывает больше интереса, т.к. даже в отсутствии линейного перемещения всё равно задействованы все оси вращения для перемещения фланцевой точки, одновременно соблюдая ориентацию РО. Впрочем, переход от первого режима ко второму происходит с добавлением всего лишь одной операции вычитания векторов для нахождения вектора (см. п. 1).
Все выше описанные операции также программировались в среде Matlab. В общих чертах структура программы следующая:
- Калибровка при запуске. Устанавливаем всё хозяйство в исходное положение и не смея прикасаться калибруем модуль БИНС по некоторому количеству сырых данных с него. Калибровка необходима, поскольку нужно убрать начальное смещение, которое выдавал фильтр (я не стал разбираться почему, и так работало прекрасно).
- Начало скрипта. Инициализируем все библиотеки и переменные, задаёмся начальным положение фланцевой или конечной точки РО.
- Запуск цикла. На каждой итерации опрашиваем датчики, находим кватернион, переводим его в матрицу, которая есть базис , он же базис, в котором расположен РО. Первый столбец принимаем за ориентацию РО и находим все обобщенные координаты, используя математические соображения из п. 1.
- Зная обобщенные координаты в прошлый момент времени и в настоящий, рассчитываем угловые скорости вращения осей.
- Отправляем пакет данных на микроконтроллер манипулятора.
Получилось конечно корявенько, но если приглянуться, то можно увидеть положительный результат исследования. Эта работа, безусловно, не претендует на законченную и требует ещё много усилий для доработки, но только в том случае, если этому можно найти применение. Но конкретное применение я ещё не нашёл… Может кто подскажет?
Источник
