[Из песочницы] Цвет Луны и Солнца из космоса в значениях RGB и цветовой температуры

20.03.2019

Казалось бы, вопрос цвета Луны и Солнца из космоса для современной науки настолько простой, что в нашем веке совсем не должно возникать проблем с ответом. Речь идёт о цветах при наблюдении именно из космоса, т. к. атмосфера приводит к изменению цвета из-за рэлеевского рассеяния света. «Наверняка где-нибудь в энциклопедии об этом подробно, в числах уже давно написано» – скажете вы. Хорошо, прямо сейчас попробуйте поискать в Интернете об этом информацию. Получилось? Скорее всего, нет. Максимум, что вы найдёте – это пара слов о том, что Луна имеет буроватый оттенок, а Солнце – красноватый. Но вы не найдёте информацию о том, видны ли эти оттенки для человеческого глаза или нет, уж тем более значения цветов в RGB или хотя бы цветовые температуры. Зато вы найдёте кучу фотографий и видео, где Луна из космоса изображена абсолютно серой, в основном на фотографиях американской программы «Аполлон», и где Солнце из космоса изображено белым и даже голубым.

Сугубо моё личное мнение – это не что иное, как следствие вмешательства политики в науку. Ведь цвета Луны и Солнца из космоса непосредственно касаются полётов американцев на Луну.

Я перерыл множество научных статей и книг в поисках информации о цвете Луны и Солнца из космоса. К счастью, оказалось, что хоть в них нет прямого ответа в RGB, но есть полная информация о спектральной плотности излучения Солнца и отражательной способности Луны по спектру. Этого вполне достаточно, чтобы получить точные цвета в значениях RGB. Надо всего лишь аккуратно посчитать, что, собственно, я и сделал. В этой статье я с вами поделюсь результатами расчётов и, естественно, подробно расскажу о самих расчётах. И вы увидите Луну и Солнце из космоса в настоящих цветах!

Расчёты я проводил в программе Mathcad и, соответственно, фрагменты кода будут на встроенном языке программирования, который вполне годится в качестве понятного для всех псевдокода.

Заодно подробно расскажу, что же такое цветовая модель RGB, с которой, я думаю, вы все знакомы. Этот вопрос на самом деле тоже не совсем простой. К примеру, попробуйте ответить на следующие два вопроса. Пусть задан цвет rgb(120,80,100).

Какие значения RGB имеет цвет, который в 2 раза темнее заданного?
Какие значения RGB у серого цвета такой же яркости, как у заданного?

Казалось бы, что тут думать, поделить на 2 в первом случае, т. е. rgb(60,40,50) и усреднить во втором случае, т. е. rgb(100,100,100). Увы, правильные ответы: 1) rgb(86,56,71); 2) rgb(92,92,92). Вы узнаете, почему ответы именно такие.

Также расскажу о цветовой температуре и как её вычислить.

Цветовое пространство XYZ

XYZ — это эталонная цветовая модель, заданная в строгом математическом смысле организацией CIE (International Commission on Illumination — Международная комиссия по освещению) в 1931 году. Модель CIE XYZ является мастер-моделью практически всех остальных цветовых моделей, используемых в технических областях. Цвет XYZ задаётся следующим образом:

$$$display$$X=int _{390,nm}^{830,nm}I(lambda ),{overline {x}}(lambda ),dlambda \ Y=int _{390,nm}^{830,nm}I(lambda ),{overline {y}}(lambda ),dlambda \ Z=int _{390,nm}^{830,nm}I(lambda ),{overline {z}}(lambda ),dlambda$$display$$$

где $$inline$I(lambda )$inline$$ — спектральная плотность какой-либо энергетической фотометрической величины (например потока излучения, энергетической яркости и т. п., в абсолютном или относительном выражении) на диапазоне длин волн от 390 до 830 нм (это по данным 2006 года, в 1931 году диапазон был от 380 до 780 нм); $$inline${overline {x}}(lambda )$inline$$ , $$inline${overline {y}}(lambda )$inline$$ , $$inline${overline {z}}(lambda )$inline$$ — функции цветового соответствия. Причём, что для нас важно, координата Y соответствует визуальной яркости сигнала.

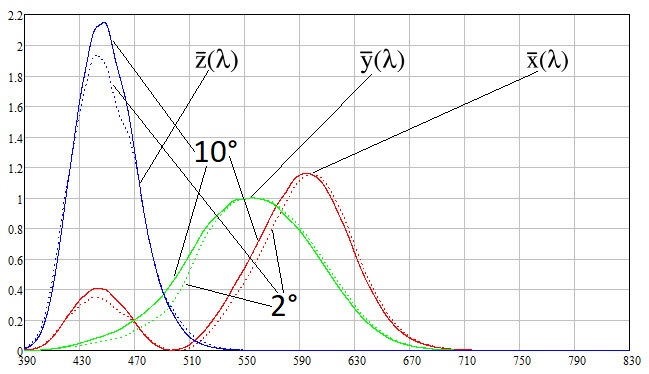
Данные функций цветового соответствия я скачал отсюда: [1].Там функции цветового соответствия определены для 2-градусного и 10-градусного поля зрения. Я решил провести расчёты для обоих случаев, сравнить результаты и убедиться, что, как и следует ожидать, цветовые координаты отличаются незначительно. Я, естественно, использовал данные функций с максимальным разрешением из предоставленных, т. е. с шагом 0.1 нм. Графики функций цветового соответствия выглядят следующим образом:

Из графиков видно, что выше 710 нм функции становятся пренебрежимо малыми в том смысле, что при наблюдении цвета близкого к белому, спектральная плотность на диапазоне выше 710 нм практически не вносит никакого вклада. Хотя мы знаем, что видимый свет лежит на диапазоне до 780 нм, но надо понимать, что это при монохроматическом излучении. Я всё это к тому, что в расчётах мне пришлось в некоторых случаях экстраполировать недостающие данные отражательной способности Луны как раз на тот диапазон, где функции цветового соответствия существенно малы. Поэтому возможная ошибка экстраполяции не приводит к заметной ошибке в вычисленных цветах.

Указанные интегралы я вычисляю методом трапеций: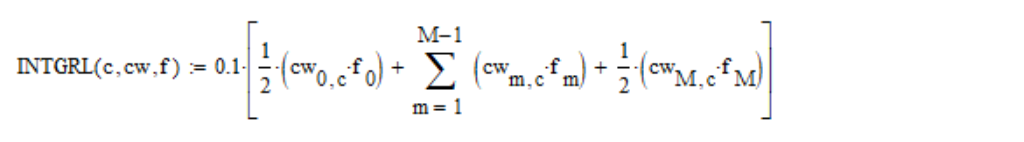

где c – номер координаты цветового пространства (1, 2, 3 для X, Y, Z соответственно); cw – таблица функций цветового соответствия; f – спектральная плотность; M=(830-390)/0.1=4400 – количество шагов сетки.

Правильные функции цветового соответствия обладают тем свойством, что площадь под всеми тремя кривыми одинакова:

$$$display$$int _{390,nm}^{830,nm} ,{overline {x}}(lambda ),dlambda,=int _{390,nm}^{830,nm} ,{overline {y}}(lambda ),dlambda,=int _{390,nm}^{830,nm} ,{overline {z}}(lambda ),dlambda$$display$$$

Это делается для того, чтобы равномерный спектр имел одинаковые значения координат XYZ. Проверим, выполняется ли это свойство: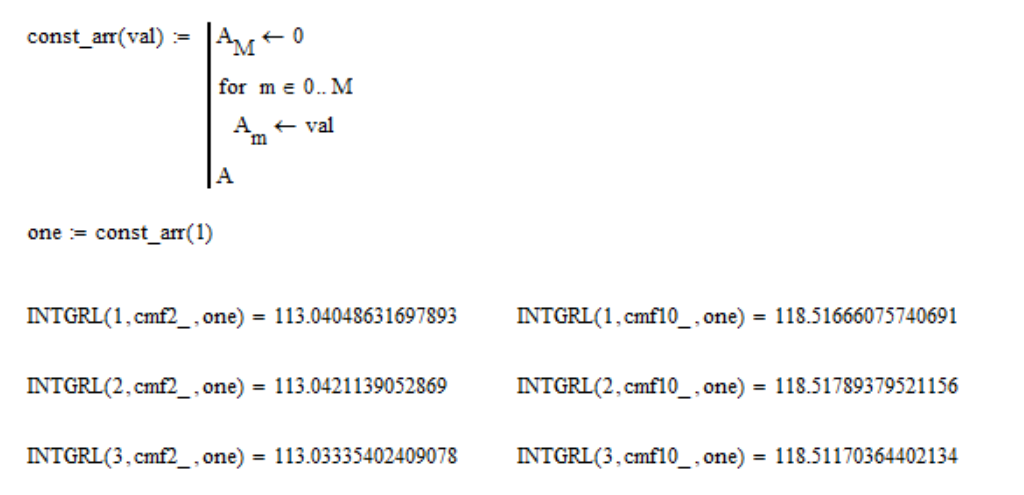

где one – массив из 1; cmf2_ и cmf10_ – таблицы функций цветового соответствия для 2-градусного и 10-градусного поля зрения соответственно. Как видим, свойство выполняется примерно с точностью 0.01%, что весьма неплохо. Но всё же, перенормируем функции для верности:

Нормировка по яркости

Рассмотрим работу цифрового фотоаппарата. Основным элементом цифрового фотоаппарата является матрица, которая состоит из фотосенсоров. При проецировании изображения на матрицу, в каждом её фотосенсоре накапливается электрический заряд, пропорциональный энергии облучения фотосенсора. Фотосенсоры фиксируют яркость элемента изображения, не неся никакой информации о его цвете. Для получения информации о цвете матрицу фотосенсоров сверху накрывают матрицей миниатюрных светофильтров. Эти светофильтры выполняют роль функций цветового соответствия. Каждый пиксель состоит из нескольких фотосенсоров, на которые в сумме наложены всевозможные светофильтры.

Таким образом, в качестве функции $$inline$I(lambda )$inline$$ нам следует брать спектральную плотность энергии облучения одного пикселя. Такую спектральную плотность можно представить в виде

$$$display$$I(lambda)=coef cdot illumination(lambda) cdot albedo(lambda)$$display$$$

где illumination – спектральная плотность излучения источника света; albedo – отражательная способность поверхности фотографируемого объекта; coef – некоторый постоянный коэффициент, который определяется временем экспозиции, диафрагмой, расстоянием от источника света до фотографируемого объекта и другими факторами. Под отражательной способностью подразумевается видимое альбедо, которое определяется как отношение яркости плоского элемента поверхности, освещенного параллельным пучком лучей, к яркости абсолютно белой поверхности, расположенной перпендикулярно к лучам.

Теперь представим, что мы выполняем работу фотоэкспонометра, с помощью которого фотограф устанавливает выдержку и диафрагму на фотоаппарате. Другими словами, нам нужно подобрать значение coef такое, чтобы снимок получился нормальным по яркости, не слишком тёмным, не слишком ярким. Представим, что за фотографируемым объектом расположен абсолютно белый экран. Отражательная способность albedo такого экрана по определению равна 1 на всех длинах волны. Зададим значение coef таким, чтобы визуальная яркость Y этого экрана на снимке была равна 1. Почему 1? Потому что в цветовой модели RGB максимально возможно значение яркости равно 1, которое достигается при rgb(255,255,255), т. е. при белом цвете. Об этом я чуть позже расскажу. Поскольку обычные тела по цвету темнее абсолютно белого экрана, изображения будут получаться нормальными по яркости. Из указанных соображений мы получаем следующее выражение для coef:

$$$display$$coef = frac{1}{int _{390,nm}^{830,nm}illumination(lambda ),{overline {y}}(lambda ),dlambda}$$display$$$

Следует отметить, что такая нормировка не гарантирует, что значение каждой координаты RGB будет меньше или равно 255. К примеру, если снять абсолютно белый экран при красном источнике света, то цвет RGB зашкалит.

Итак, значения координат цветового пространства XYZ я вычисляю следующим образом: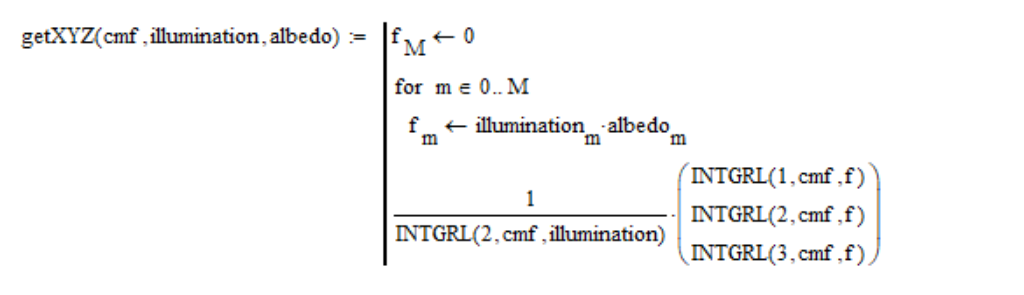

Нам необходимо как-то выразить цвет Солнца. Фотографировать его напрямую мы не можем, да и в нашей математической модели мы такой экстремальный случай не предусмотрели. Очевидно, нам нужно сфотографировать освещённую Солнцем поверхность белого цвета. Поскольку Солнце из космоса имеет красноватый оттенок, то, как я уже говорил, цвет абсолютно белого экрана при этом зашкаливает. Поэтому надо брать поверхность потемнее. Я опытным путём установил, что надо брать белую бумагу с альбедо 0.91. Больше альбедо брать нельзя, начинает зашкаливать. Таким образом, чтобы получить цвет Солнца, я просто в вышеуказанной формуле устанавливаю значение albedo равным 0.91 на всех длинах волны:

Цветовое пространство sRGB

Наиболее распространённое цветовое пространство с использованием модели RGB — sRGB. Поэтому, когда говорят про RGB без уточнений, подразумевают именно цветовое пространство sRGB, которое является стандартом представления цветового спектра с использованием модели RGB. Данный стандарт был создан Международным консорциумом по цвету (англ. International Color Consortium, ICC) в 1996 году для унификации использования модели RGB в мониторах, принтерах и Интернет-сайтах. Давайте разберём этот стандарт, описание которого доступно по адресу [2].

Преобразование XYZ в sRGB происходит в три этапа. Сначала координаты XYZ преобразуются в линейные координаты RGB, затем линейные координаты преобразуются в нелинейные координаты RGB, и в конце нелинейные координаты преобразуются в 8-битные координаты RGB, которые, собственно, являются координатами цветового пространства sRGB.

Преобразование координат XYZ в линейные координаты RGB происходит следующим образом:

а обратное – так:

Интересно, откуда же взялись эти странные числа в квадратных матрицах? А взялись они из рекомендации ITU-R BT.709 [3]. Обозначим первую квадратную матрицу через XYZ_to_RGB, а вторую – через RGB_to_XYZ. Очевидно, они взаимно обратны. В рекомендации ITU-R BT.709 заданы требования, которые должны выполняться для второй матрицы. Из этих требований можно однозначно вычислить вторую матрицу, а первая равна обратной матрице второй.

Введём следующие функции:

$$$display$$XYZ(R,G,B) = RGB_to_XYZ cdot {begin{bmatrix} R \ G \ B end{bmatrix}} \ W(R,G,B) = XYZ_1(R,G,B) + XYZ_2(R,G,B) + XYZ_3(R,G,B) \ xy(R,G,B) = frac {1} {W(R,G,B)} cdot {begin{bmatrix} XYZ_1(R,G,B) \ XYZ_2(R,G,B) end{bmatrix}}$$display$$$

Тогда требования рекомендации ITU-R BT.709 принимают следующий вид:

$$$display$$xy(1,0,0) = {begin{bmatrix} 0.64 \ 0.33 end{bmatrix}} , ; xy(0,1,0) = {begin{bmatrix} 0.30 \ 0.60 end{bmatrix}} , ; xy(0,0,1) = {begin{bmatrix} 0.15 \ 0.06 end{bmatrix}} \ xy(1,1,1) = {begin{bmatrix} 0.3127 \ 0.3290 end{bmatrix}}$$display$$$

Имеем 8 уравнений, когда у нас 9 неизвестных элементов матрицы RGB_to_XYZ, т. е. не хватает ещё одного уравнения. А не хватающее уравнение задано неявно, мне пришлось самому догадаться до него. Суть этого уравнения состоит в том, что для белого цвета визуальная яркость Y должна быть равна 1:

$$$display$$XYZ_2(1,1,1)=1$$display$$$

Я нашёл точное решение этих уравнений в рациональных числах:

Если округлить числа в моём результате до четырёх знаков после запятой, то получатся как раз те самые странные числа в стандарте Международного консорциума по цвету. Я же в своих расчётах использую не округлённые матрицы, а вышеуказанные точные (насколько позволяют числа с плавающей запятой двойной точности).

Итак, линейные координаты RGB на основе таблицы функций цветового соответствия (cmf), спектральной плотности излучения (illumination) и отражательной способности (albedo) я вычисляю следующим образом:

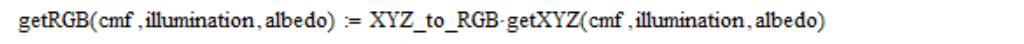
Также я применяю линейные координаты RGB, усреднённые по 2-градусному и 10-градусному полю зрения:

Из линейных координат RGB визуальная яркость Y вычисляется по такой формуле (по умолчанию массивы Mathcad нумеруются с нулевого элемента):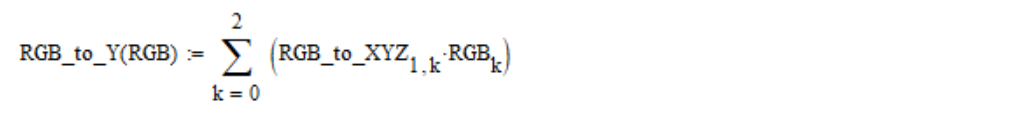

Продолжаем разбирать стандарт. Каждая линейная координата RGB преобразуется в нелинейную с помощью нелинейной функции lin2bit, а обратно – bit2lin, которые определены следующим образом:

Графики этих функций выглядят так:

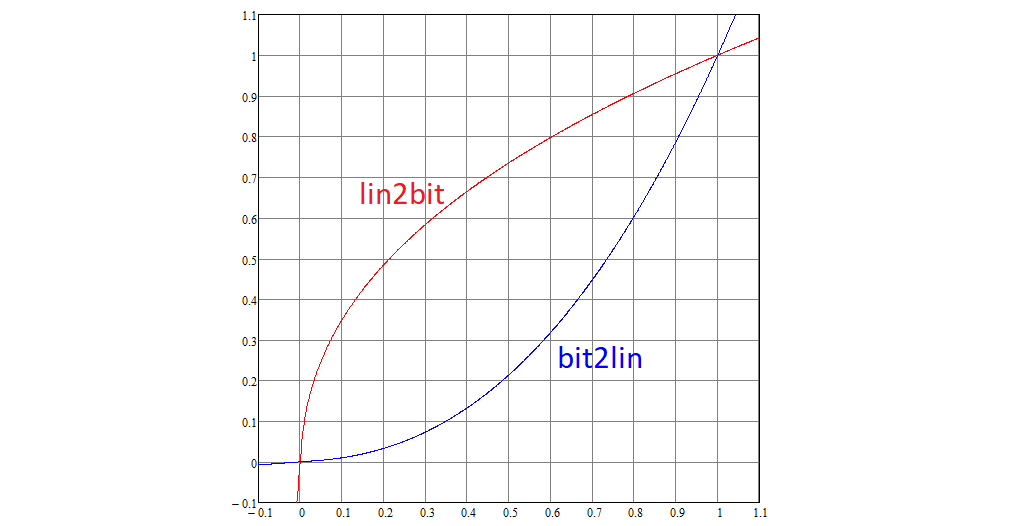
Обратите внимание, 0 преобразуется в 0, 1 в 1.

В конце нелинейные координаты RGB преобразуются в 8-битные умножением на 255 с последующим округлением до целых чисел.

Таким образом, я определил следующие функции для преобразования линейных координат RGB в 8-битные и обратно:

Теперь мы готовы решить задачу из введения. Напоминаю условие.

Пусть задан цвет rgb(120,80,100).
1) Какие значения RGB имеет цвет, который в 2 раза темнее заданного?
2) Какие значения RGB у серого цвета такой же яркости, как у заданного?

Решение:

Ответы: 1) rgb(86,56,71); 2) rgb(92,92,92).

Цветовая температура

Цветовая температура источника света, измеряемая в Кельвинах, определяется температурой абсолютно чёрного тела, расположенного на цветовой диаграмме там же, где и рассматриваемый источник излучения. Если источник света не попадает на кривую Планка (кривая, которая определяется множеством цветовых точек абсолютно чёрного тела при различных температурах), для его характеристики используется коррелированная цветовая температура. Эта величина также измеряется в Кельвинах и определяется температурой абсолютно чёрного тела, цвет которого максимально приближен к цвету источника света. Для нахождения коррелированной цветовой температуры источника излучения на цветовой диаграмме, построенной в координатах (u,v), определяется самая близкая к источнику точка на кривой Планка (т. е. самое короткое геометрическое расстояние). Температура чёрного тела, расположенного в этой точке, и будет соответствовать коррелированной цветовой температуре рассматриваемого источника [4].

Для абсолютно чёрного тела температуры T мощность излучения на единицу площади излучающей поверхности в единичном интервале длин волн выражается законом Планка:

$$$display$$ R(lambda, T) = frac {2 pi h c^2} {lambda^5} frac {1} {e ^ {h c / lambda k T}-1}$$display$$$

Соответственно, спектральную плотность излучения абсолютно чёрного тела я вычисляю следующим образом (в нулевой колонке таблицы функций цветового соответствия cmf2 находятся значения длин волн в нанометрах):

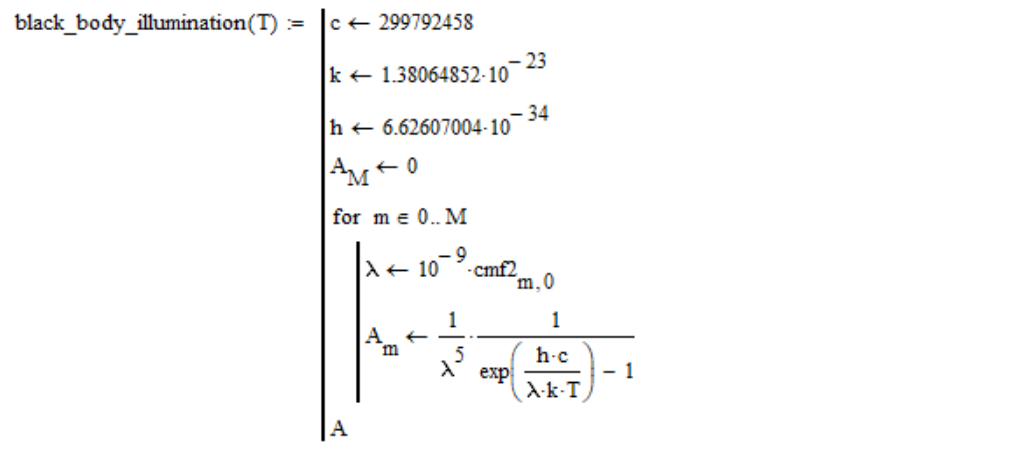
Обратите внимание, я опустил постоянный множитель, т. к. он всё равно сокращается при дальнейшей нормировке по яркости (на цветовую температуру яркость источника света не влияет).

Далее вычисляю линейные координаты RGB:

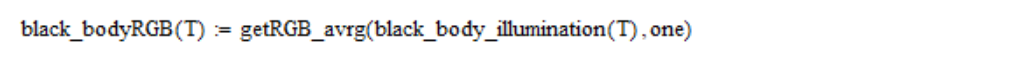
Линейные координаты RGB преобразуются в координаты (u,v) следующим образом:

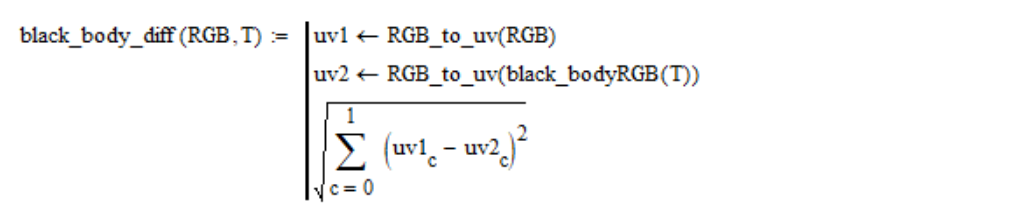
На плоскости (u,v) вычисляется геометрическое расстояние межу точками рассматриваемого цвета и цвета абсолютно чёрного тела заданной температуры T:

К примеру, для стандартного источника белого света зависимость этого расстояния от температуры выглядит так:

Значение T, при котором эта зависимость имеет минимум, является цветовой температурой рассматриваемого источника света.

Спектральная плотность излучения Солнца

Данные спектральной плотности излучения Солнца в отсутствии атмосферы я скачал отсюда: [5]. Источник света, соответствующий Солнцу из космоса, я в дальнейшем буду обозначать как E490. Также для сравнения в расчётах я рассматриваю стандартный источник света D65. Этот источник представляет белый свет. Я рассматриваю его для того, чтобы показать, как выглядела бы Луна, если бы Солнце было белым. Данные спектральной плотности излучения стандартного источника света D65 я скачал отсюда: [6].

Как будет показано ниже, источники света D65 и E490 имеют цветовые температуры 6467K и 5912K соответственно. Спектральные плотности излучения источников света D65, E490 и абсолютно чёрных тел соответствующих температур выглядят следующим образом:

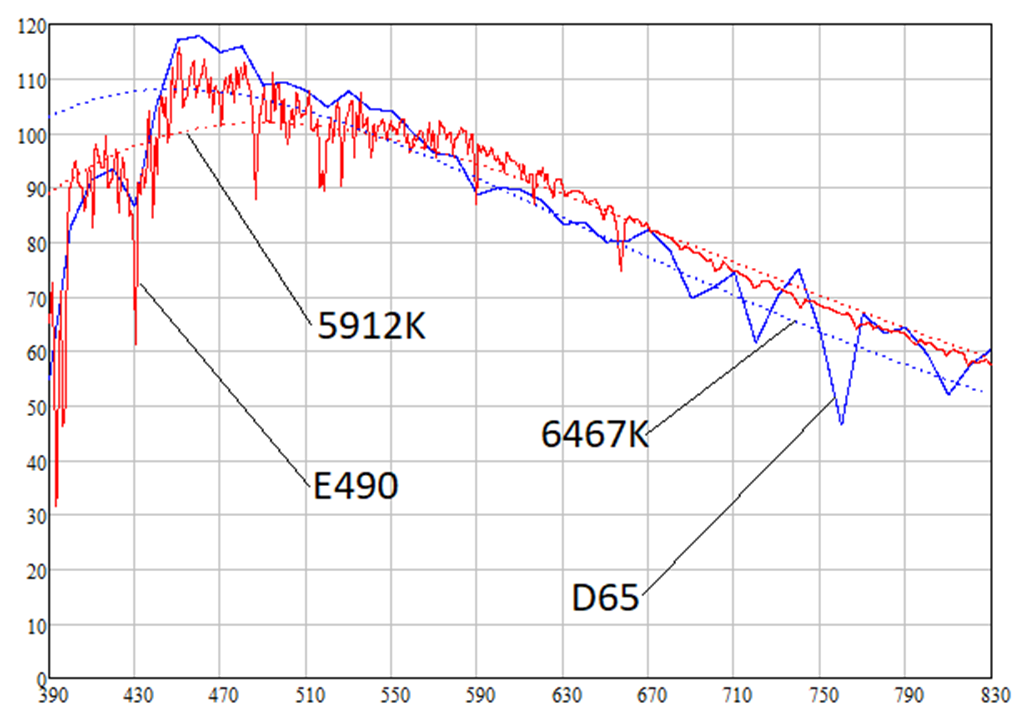
Можно заметить, что спектральная плотность излучения Солнца выше, чем у белого источника света на более длинных волнах, т. е. на длинах волн красного света (620-770 нм). Это значит, что Солнце имеет красноватый оттенок. Действительно, расчёты дают следующие цвета источников света D65, E490 и абсолютно чёрных тел соответствующих температур (как я уже говорил, рассматривается белая бумага с альбедо 0.91):

Обратите внимание, координаты sRGB у Солнца и абсолютно чёрного тела температуры 5912K точно совпадают. Это ничем не объясняется, просто так получается.

Цвет кружочков на последней картинке – это настоящий цвет Солнца из космоса. Человеческий глаз чётко видит красноватый оттенок Солнца. Так что, то, что Солнце из космоса белое – это большой миф! Следует отметить, что на фотографиях и видео программы «Аполлон» этот оттенок почему-то не наблюдается. На настоящих снимках видимый красноватый оттенок Солнца непременно проявился бы на белых поверхностях американского флага и скафандров. И как будет показано ниже, этот оттенок Солнца даёт заметный вклад в «красноту» Луны из космоса.

Луна по цвету разная или одинаковая?

Противники теории лунного заговора продвигают версию, что Луна по цвету разная. Якобы местами Луна серая, местами – коричневая, и при этом «Аполлоны» высаживались там, где Луна серая. Но эта версия прямо противоречит научным данным. В статье [7] явно написано:

Цветовые различия на Луне крайне малы.

Также Шевченко в своей книге [8] пишет:

Много лет в этом направлении работал известный американский исследователь Т. Мак-Корд. Им было получено более 200 спектров для различных участков лунной поверхности размером 10-20 км каждый. Все полученные кривые в основном сходны по виду.

Так что, нет, Луна по цвету не разная, а одинаковая.

Данные о цвете Луны по Шевченко

Шевченко в своей книге [8] приводит следующую зависимость отражательной способности от длины волны.

В своих расчётах я применяю кусочно-линейную интерполяцию этих данных. Недостающие данные на интервале 820-830 нм я получил прямым продолжением отрезка на интервале 690-820 нм.

Данные о цвете Луны по LRO

В работе [9] приведена зависимость отражательной способности лунной поверхности от условий освещения и наблюдения на длинах волны от 321 нм до 689 нм. Параметры модели были вычислены на основе анализа данных, полученных Лунным разведывательным орбитером (англ. Lunar Reconnaissance Orbiter, сокр. LRO). Условия освещения и наблюдения определяются тремя параметрами i (угол падения), e (угол отражения) и g (фазовый угол). Эти углы показаны на следующей схеме:

Фазовый угол можно выразить через азимутальный угол $$inline$varPsi$inline$$ с помощью сферической теоремы косинусов следующим образом:

$$$display$$g=arccosleft(cosleft(iright)cosleft(eright)+sinleft(iright)sinleft(eright)cosleft(varPsiright)right)$$display$$$

В расчётах я беру традиционные значения углов 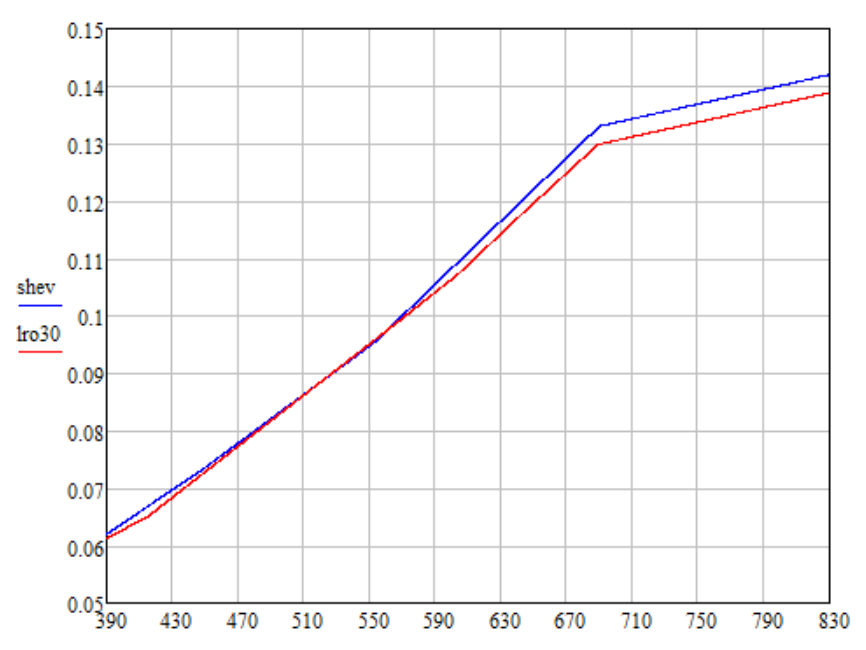i = g = 30°, e = 0°. Для таких углов получается следующая зависимость отражательной способности от длины волны (график lro30):

Я сделал линейную экстраполяцию данных LRO на интервал 689-830 нм таким образом, чтобы отношение значений в точках 830 нм и 689 нм было такое же, как у данных Шевченко (график shev).

Данные о цвете Луны по «Кагуя»

В работе [10] приведены данные, полученные вторым японским искусственным спутником Луны. К сожалению, отражательная способность в видимом диапазоне длин волн приведена с очень низким разрешением, поэтому я не использую её в своих вычислениях.

Но работа интересна тем, что в ней говорится о колоссальных расхождениях данных «Кагуя» с данными миссии «Аполлон-16». И это один из редких случаев, когда в научном сообществе открыто говорится о несоответствиях, связанных с полётами американцев на Луну.

Результаты вычислений

Дальше я буду использовать следующие обозначения:

D65 – стандартный источник белого света D65;
E490 – источник света от Солнца в отсутствии атмосферы;
Б-0.91 – белая бумага с альбедо 0.91;
LRO(30°) – данные по LRO при традиционных значениях углов i = g = 30°, e = 0°;
Shevch. – данные по Шевченко;
лин. (2°) – линейные координаты RGB при 2-градусном поле зрения;
лин. (10°) – линейные координаты RGB при 10-градусном поле зрения;
лин. (средн.) – линейные координаты RGB, усреднённые по 2-градусному и 10-градусному полю зрения;
sRGB (100%) – координаты sRGB, полученные из линейных координат RGB, усреднённых по 2-градусному и 10-градусному полю зрения;
sRGB (200%) – координаты sRGB, полученные из удвоенных линейных координат RGB, усреднённых по 2-градусному и 10-градусному полю зрения;
sRGB (300%) – координаты sRGB, полученные из утроенных линейных координат RGB, усреднённых по 2-градусному и 10-градусному полю зрения;
sRGB (400%) – координаты sRGB, полученные из учетверённых линейных координат RGB, усреднённых по 2-градусному и 10-градусному полю зрения;
цв. темп. – цветовая температура, полученная из линейных координат RGB, усреднённых по 2-градусному и 10-градусному полю зрения;

D65

Б-0.91 LRO(30°) Shevch.

лин. (2°) 0.9076,0.9120,0.8968 0.1177,0.0931,0.0688 0.1202,0.0931,0.0697

лин. (10°) 0.9084,0.9122,0.8929 0.1165,0.0916,0.0687 0.1188,0.0917,0.0696

лин. (средн.) 0.9080,0.9121,0.8948 0.1171,0.0924,0.0688 0.1195,0.0924,0.0697

sRGB (100%) rgb(244,245,243) rgb(96,86,74) rgb(97,86,75)

sRGB (200%) — rgb(133,119,104) rgb(134,119,104)

sRGB (300%) — rgb(160,144,125) rgb(161,144,126)

sRGB (400%) — rgb(182,164,143) rgb(184,164,144)

цв. темп. 6467K 4928K 4891K

	Б-0.91	LRO(30°)	Shevch.
лин. (2°)	0.9076,0.9120,0.8968	0.1177,0.0931,0.0688	0.1202,0.0931,0.0697
лин. (10°)	0.9084,0.9122,0.8929	0.1165,0.0916,0.0687	0.1188,0.0917,0.0696
лин. (средн.)	0.9080,0.9121,0.8948	0.1171,0.0924,0.0688	0.1195,0.0924,0.0697
sRGB (100%)	rgb(244,245,243)	rgb(96,86,74)	rgb(97,86,75)
sRGB (200%)	—	rgb(133,119,104)	rgb(134,119,104)
sRGB (300%)	—	rgb(160,144,125)	rgb(161,144,126)
sRGB (400%)	—	rgb(182,164,143)	rgb(184,164,144)
цв. темп.	6467K	4928K	4891K

E490

Б-0.91 LRO(30°) Shevch.

лин. (2°) 1.0005,0.8892,0.8490 0.1283,0.0909,0.0649 0.1310,0.0909,0.0657

лин. (10°) 1.0021,0.8888,0.8483 0.1272,0.0895,0.0650 0.1297,0.0895,0.0659

лин. (средн.) 1.0013,0.8890,0.8486 0.1277,0.0902,0.0649 0.1303,0.0902,0.0658

sRGB (100%) rgb(255,242,237) rgb(100,85,72) rgb(101,85,73)

sRGB (200%) — rgb(138,118,101) rgb(140,118,102)

sRGB (300%) — rgb(166,142,122) rgb(168,142,123)

sRGB (400%) — rgb(189,162,139) rgb(191,162,140)

цв. темп. 5912K 4550K 4512K

	Б-0.91	LRO(30°)	Shevch.
лин. (2°)	1.0005,0.8892,0.8490	0.1283,0.0909,0.0649	0.1310,0.0909,0.0657
лин. (10°)	1.0021,0.8888,0.8483	0.1272,0.0895,0.0650	0.1297,0.0895,0.0659
лин. (средн.)	1.0013,0.8890,0.8486	0.1277,0.0902,0.0649	0.1303,0.0902,0.0658
sRGB (100%)	rgb(255,242,237)	rgb(100,85,72)	rgb(101,85,73)
sRGB (200%)	—	rgb(138,118,101)	rgb(140,118,102)
sRGB (300%)	—	rgb(166,142,122)	rgb(168,142,123)
sRGB (400%)	—	rgb(189,162,139)	rgb(191,162,140)
цв. темп.	5912K	4550K	4512K

На следующем изображении приведены цвета поверхности Луны sRGB (100%), sRGB (200%) (удвоенная яркость), sRGB (300%) (утроенная яркость), sRGB (400%) (учетверённая яркость) при источнике света E490 (т. е. при наблюдении из космоса) согласно данным LRO и Шевченко.

Как видите, Луна из космоса имеет коричневый цвет как по данным LRO, так и по данным Шевченко. По Шевченко получается немного (еле заметно) краснее, чем по LRO.

Цвет Луны на фотографиях

В данном разделе мы займёмся раскраской фотографий. Пусть дано изображение img и цвет в линейных координатах RGB. Каждый пиксель изображения заменим пикселем заданного цвета такой же яркости, как у цвета исходного пикселя. Изображение в программе Mathcad представляется в виде одной матрицы координат sRGB, которая получается сшиванием трёх матриц “R”, “G”, “B” слева направо. С учётом этого процедура раскраски выглядит следующим образом: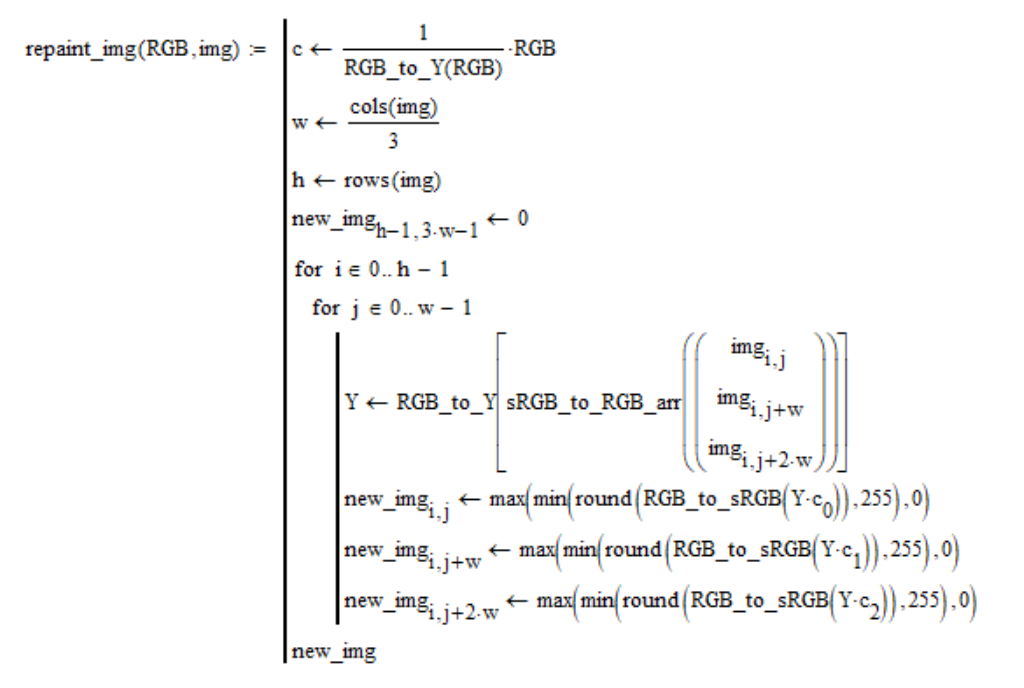

Для интереса я взял фотографии с изображением лунной поверхности из фотоальбомов американской программы «Аполлон» и перекрасил в цвета, полученные из моих расчётов. Я привожу лишь результаты, а вывод о том, подлинные эти фотографии или фальшивые, сделайте сами.

Результат раскраски фотографии AS11-44-6552:

В середине расположены исходные фотографии. Cлева фотографии раскрашены в цвета согласно данным LRO при традиционных значениях углов i = g = 30°, e = 0°, а справа – согласно данным Шевченко. Верхний ряд соответствует стандартному источнику света D65, т. е. в верхнем ряду показаны цвета поверхности Луны, которые получались бы, если бы Солнце было белым. Нижний ряд соответствует источнику света E490, т. е. в нижнем ряду показаны естественные цвета поверхности Луны при наблюдении из космоса.

Как видите, красноватый оттенок Солнца дает заметный вклад в «красноту» поверхности Луны, которая в итоге выглядит коричневой, а никак не серой.

Серый цвет Луны на фотографиях НАСА можно было бы объяснить тем, что плёнка по некоторым причинам «ушла» в синий цвет, но эта версия сразу же отпадает, если проанализировать снимки градаций серого цвета в конце альбомов. На фотографии as11-44-chart приведён такой снимок для последней вышеуказанной фотографии. Я на эту фотографию наложил слева от градаций серого цвета настоящие серые цвета той же яркости, что и на фотографии, и также выписал значения координат sRGB. В итоге получилась следующее изображение:

Как видите, плёнка не только не «ушла» в синий цвет, а даже немного «ушла» в противоположную сторону от синего цвета. Такое отклонение никак не может превратить коричневый цвет в серый.

Результат раскраски фотографии AS11-40-5903:

На исходной фотографии лунная поверхность местами имеет не просто серый цвет, а даже небольшой синеватый оттенок. На фотографии as11-40-chart приведён соответствующий снимок градаций серого цвета:

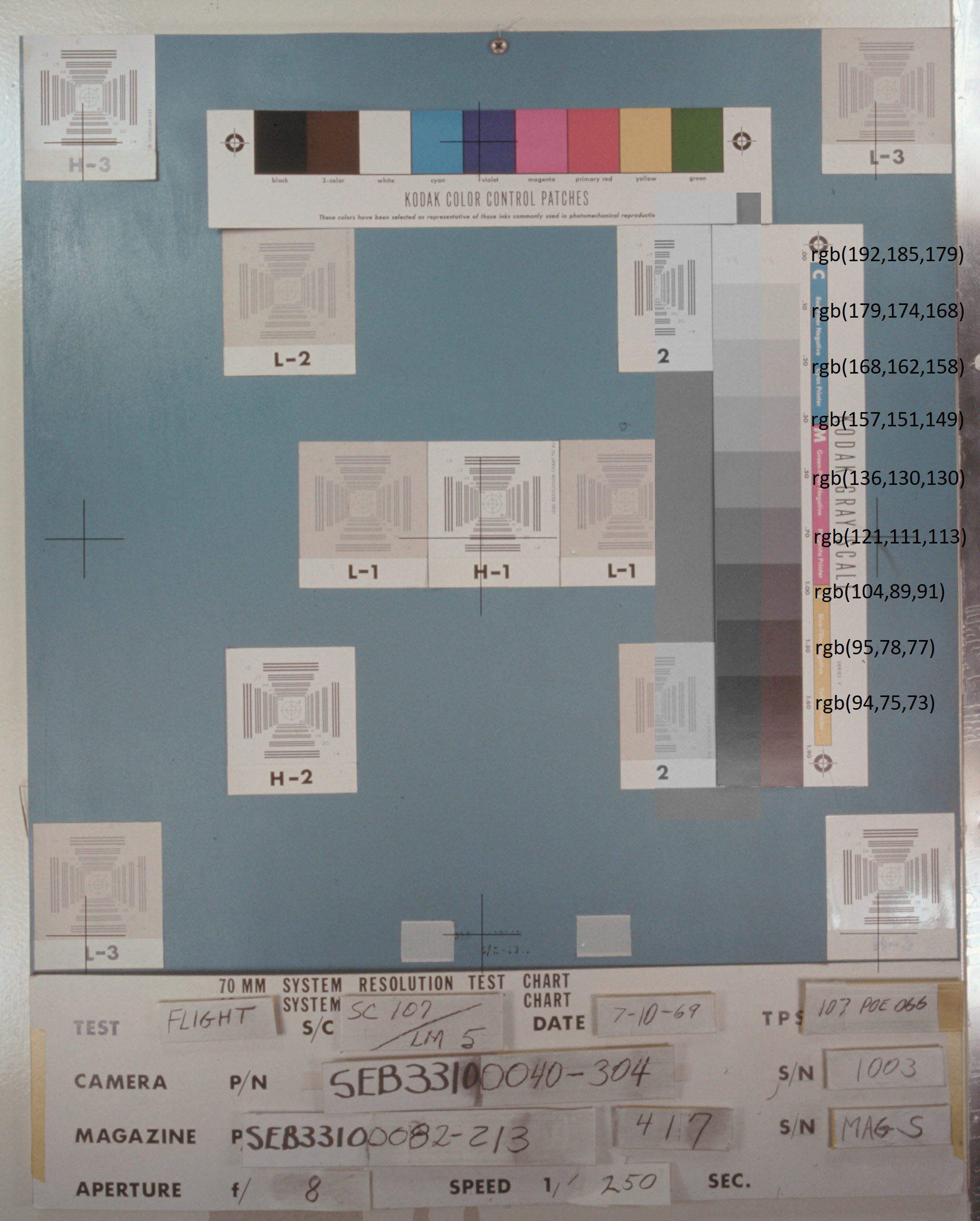
Плёнка «ушла» не в «синий» цвет, а в «красный». И даже после этого почему-то лунная поверхность на фотографии НАСА имеет серый цвет.

Результат раскраски фотографии AS11-37-5455:

Это одна из редких фотографий программы «Аполлон», где лунная поверхность имеет коричневый оттенок, пусть и не целиком. Её любят показывать противники теории лунного заговора, мол, смотрите, коричневая же. Но здесь закрался подвох. Проанализируем фотографию as11-37-chart, на которой приведён соответствующий снимок градаций серого цвета:

Плёнка просто «ушла» в коричневый цвет. Вот и вся причина коричневого оттенка лунной поверхности на фотографиях НАСА.

Зависимость цвета лунной поверхности от условий освещения и наблюдения

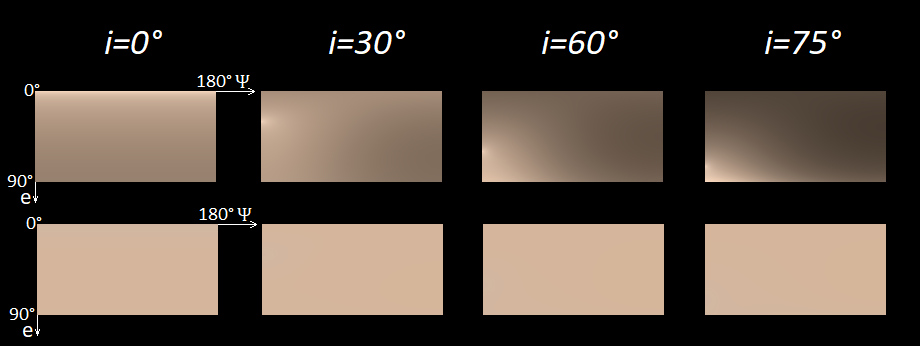
Используя данные LRO, приведённые в работе [9], исследуем, как меняется цвет поверхности Луны от условий освещения и наблюдения. Рассмотрим источник света E490 (Солнце из космоса) и разные значения углов i, e, $$inline$varPsi$inline$$ . На следующей картинке показан результат, где в верхнем ряду представлены цвета с трёхкратной яркостью, а в нижнем – цвета, приведённые к одной и той же яркости Y = 0.5.

Как видно из картинки, меняется только яркость. В нижем ряду цвета практически одинаковые везде для человеческого глаза. Хотя, если присмотреться, в случае i = 0° можно увидеть очень слабое отклонение в серую сторону при приближении e к нулю.

Цвет лунного грунта

На сайте НАСА имеется очень странная фотография, а именно это фотография пробы лунного грунта № 10005.

Лунный грунт на фотографии выглядит коричневым, даже слишком коричневым с учётом того, что освещение производилось белым источником света. Правильность баланса белого можно проверить по цвету белой бумаги, которая попала в кадр.

Может это тот самый оранжевый грунт, который обнаружили астронавты «Аполлона-17»? Нет! В документе [11] чётко зафиксировано, что проба была взята астронавтами «Аполлона-11».

А теперь послушаем, что говорит Нил Армстронг (астронавт «Аполлона-11») в интервью Патрику Муру [12], которое он дал в 1970 году.

Когда вы смотрите на грунт вблизи или в руке, вы обнаруживаете, что на самом деле он угольно-серый, и мы особо не могли найти ничего отличного от этого цвета.

(When you look at the material at close range, as if in your hand, you find it’s a charcoal gray in fact, and we were never able to find any things that were very different from that color.)

Выходит, Нил Армстронг, не побоюсь этого слова, соврал.