Всем известно, что классическая механика является предельным случаем квантовой с одной стороны и теории относительности – с другой. Последние две наиболее точно описывают реальность, в то время как первая считается лишь удобным частным случаем. Из квантовой физики можно получить классическую, но не наоборот.
Еще один важный момент заключается в том, что многими по умолчанию подразумевается полнота волновой функции и фундаментальность уравнения Шредингера.
Таким образом, основные физические законы, необходимые для математической теории значительной части физики и всей химии, полностью известны, и трудность заключается лишь в том, что точное применение этих законов приводит к уравнениям, которые слишком сложны, чтобы быть разрешимыми. Поэтому становится желательным разработать приближенные практические методы применения квантовой механики, которые могут привести к объяснению основных особенностей сложных атомных систем без слишком больших вычислений.
П. Дирак
Но догмы имеют обыденность рушиться: теоремы о запрете признаются несостоятельными, скрытые переменные (как локальные так и не очень) имеют место быть, энтропия замкнутой системы может уменьшаться, а убеждения касательно кривизны вселенной регулярно обламываются новыми измерениями.
С момента создания квантовой механики и до сих пор продолжаются дискуссии об онтологии теории и ее интерпретациях. Онтологическая проблема особенно ярко проявляется в вопросе об измерении. Поэтому понимание физического смысла волновой функции имеет первостепенное значение. А чтобы понять волновую функцию, нужно понять уравнения квантовой физики.
Знаменитое уравнение Шредингера математически близко к обычному уравнению диффузии. Главное отличие в том, что время становится мнимым, то есть происходит поворот Вика. Это означает, что классическое и квантовое частично связаны поворотом на 90 градусов в комплексной плоскости (умножением на мнимую единицу). Уравнение Шредингера задается:
(Сопутствующий философский бред можно найти в эмоциональной статье)
Ричард Фейнман в своих знаменитых лекциях писал:
Мы не хотим, чтобы вы думали, что мы вывели уравнение Шредингера, но хотим показать вам лишь способ рассуждения. Когда Шредингер впервые записал его, он дал своего рода вывод, основанный на некоторых эвристических аргументах и блестящих интуитивных догадках. Некоторые из аргументов, которые он использовал, были даже ложными, но это не имеет значения; важно только то, что конечное уравнение дает правильное описание природы. [Фейнман, Лекции по физике, II-14.1]
В литературе приводится множество эвристических способов обоснования уравнения, но в целом оно вводится как один из постулатов квантовой механики. Тем не менее недавняя статья из Nature, указывает на то, что последовательный аналитический вывод вполне осуществим.
Статья начинается с классической механики, где частицы при движении стараются минимизировать действие. С одной маленькой оговорочкой – они претерпевают марковскую диффузию. То есть вносится стохастика с сопутствующими случайными силами.
Затем, крайне непринужденно просуммировав пути (а ля фейнмановские интегралы по траекториям) и подняв теорию стохастического оптимального контроля, разумеется, с оглядкой на релятивистскую инвариантность, авторы получают уравнение Гамильтона-Якоби-Беллмана
При этом они постоянно заостряют внимание, что вместо того, чтобы постулировать правила подстановки операторов, вывод происходит полностью осмысленным образом.
На Хабре в комментах часто проскакивают очень умные мысли – нам хочется линейных дифуров. Тогда у нас будут плюшки типа суперпозиции, интерференции и линейной алгебры с разложением на собственные функции и спектральной теорией. Поэтому авторы подбирают коэффициент последнего слагаемого (сигма в квадрате) предвосхищая линейность.
Затем шаг за шагом осуществляется переход:
уравнение Гамильтона-Якоби-Беллмана -> уравнение Штекельберга -> телеграфные уравнения -> уравнения Клейна-Гордона, Дирака и нерелятивистское Шредингера.
И это восхитительно!
Во первых, мнимая природа различных переменных в квантовой механике автоматически выходит из структурой метрики Минковского. Причем авторы надеются в дальнейшем установить волновое уравнение в общем искривленном пространстве-времени. И такое обобщение метрики «возможно, было бы способом объединить общую теорию относительности и квантовую механику».
Во вторых, можно вспомнить, что происхождение правила Борна до сих пор выглядит неоднозначным. Хотя, в многомировой, клеточно-автоматной, волно-пилотной и еще в некоторых интерпретациях оно всплывает так или иначе как побочный продукт. Здесь же правило Борна естественным образом связано с реальной частью минимального ожидаемого действия. «Процесс пространственно-временной диффузии проходит по маршруту, который сводит к минимуму ожидаемое действие; в этом суть того, как вероятность (перехода) связана с минимизацией энергии.»
В третьих, подход придерживается реалистической философии квантовой механики, где реальность существует независимо от наблюдателя. Что это значит для нас?
Вспомним двухщелевой эксперимент Юнга. Интерференция света или, что еще более умозрительно, интерференция волн на поверхности жидкости вполне спокойно понимается и принимается. Но когда одиночные частицы начинают постепенно вырисовывать полосатую картину на экране, наступает разрыв шаблона.
В прошлом веке, когда у европейского общества еще не прошла эйфория после свержения божественного фатализма, философская мысль продолжала укреплять образ человека как центра вселенной. Вкупе с достижениями в области исследований разума и нахлынувшим интересом к восточной культуре, в зарождающейся квантовой физике начало возобладать представление об особой роли наблюдателя. Всю информацию о любой системе можно поместить в волновую функцию, а она в свою очередь подчиняется уравнению Шредингера – фундаментальному закону, который на удивление точно согласовался с экспериментами. Разумеется, в рамках плотностей вероятности. А реальность уже возникает в глазах смотрящего (или в душе разумеющего).
Такой взгляд сильно импонирует человеческому эго и поэтому нашел обширное распространение. Но некоторых раздражал такого рода отупляющий солипсизм. В конечном счете, коллапс наведенный разумным наблюдателем был признан нефизичным, и на его место пришла декогеренция. Тем не менее новая Копенгагенская интерпретация советует избегать вопросов о реальности, прежде чем произойдет измерение-декогеренция.
Но с прагматических позиций реализм более предпочтителен. Именно поэтому, например, бомовская интерпретация набирает популярность: частицы реально существуют и у них есть траектории, что помогает в расчетах и легче для восприятия. Так что обсуждаемая статья ближе всего к таким траекторным представлениям.

(Методику построения траекторий см. в приложении)
В теории волны-пилота частицы подчиняются нелокальному действию квантового потенциала. А показанная выше модель предполагает, что исследуемая частица движется под действием внешней случайной силы пространства-времени. Здесь нет волн коллапсирующих в частицы. Частицы просто взаимодействуют с некоторыми скрытыми степенями свободы, по жизни двигаясь зигзагами. Волновые паттерны возникают из коллективного поведения миллионов частиц. А волновая функция лишь описывает эти паттерны.
Такое случайное движение частицы индуцирует распределение вероятностей перехода. Это означает, что квантовую механику можно понимать как статистическую теорию. О причинах случайной силы будут еще много спорить, но авторы предлагают перебиться пока парочкой вариантов (раз, два).
Можно было бы сделать предположение, что квантовая механика или квантовая теория поля – это всего лишь феноменологическая теория, и причина статистической природы лежит в стохастической природе самого пространства-времени. Если пространство-время и его метрика стохастичны в масштабах Планка, это может создать иллюзию случайного движения, которое может быть феноменологически смоделировано с помощью стохастических дифференциальных уравнений в пространстве-времени. В соответствии с общей теорией относительности это, по сути, может означать, что источники энергии в пространстве-времени имеют случайный характер, который может быть вызван различными возмущениями, такими как колебание вакуума или излучение нулевого поля.
Дальнейшее чтиво
-
Здесь можно посмотреть более популярный обзор обсуждаемой статьи.
-
Далее читаем рассуждения о верности уравнения Шредингера. В принципе, на него уже давно прицепляют всяческие довески: нелинейность, память, стохастичность, так что фундаментальность это больше вопрос веры.
-
Стохастическая квантовая механика выделена в отдельную интерпретацию. Вообще, эта тема была популярна в 60-х. Чего стоит зашкварная статья, где уравнение Шредингера вывели из ньютоновской механики (правда там тоже было броуновское движение). По ней до сих пор плодятся трибьюты (раз, два, три, четыре, пять). Следует также отметить, что недавно было показано, что знаменитые соотношения неопределенности Гейзенберга в целом присущи стохастическим системам, и, как видится, они не являются уникальными для квантово-механических систем.
-
Конечно, можно зайти и со стороны электродинамики. Вот из свеженького.
-
Герард `т Хоофт (продвигающий интерпретацию клеточных автоматов) пару месяцев назад выпустил препринт, где квантовая механика эмерджентно выходит из классической. Кто знает, может его быстрые переменные и будут играть роль случайных сил. И до кучи вспоминаем, что на гравитацию тоже начинают поглядывать с эмерджентных позиций.
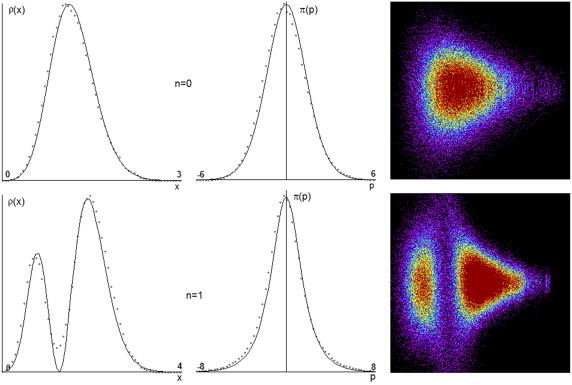
(Подробности см. в статье)
Дальше, в предложенных статьях расшариваем список литературы и Cited by, чтобы окончательно убедиться, что по теме идут серьезные сподвижки. То ли классическая детерминистичная механика ушла на задний план в ожидании когда подтянется матаппарат статистики и клеточных автоматов, чтобы затем вновь вернуться на периферию философской мысли. То ли научное сообщество устало бороться с контринтуитивностью и готово принять любую модель подразумевающую комфортную математику и простоту в объяснениях. Ответ узнают наши потомки на лекциях по философии науки.


